Similar presentations:
Численные методы решения дифференциальных уравнений
1.
Численные методы решениядифференциальных уравнений
dy
y ' y ( n ) f ( x, y )
dx
dny
(n)
(1)
(2)
y
f
(
x
,
y
,
y
,
y
,
n
dx
, y ( n 1) )
2.
Численные методы решениядифференциальных уравнений
dny
(n)
(1)
(2)
y
f
(
x
,
y
,
y
,
y
,
n
dx
, y ( n 1) )
y1 y
dy1
y
2
dx
dy2 y3
dx
dyn f ( x, y , y , y ,
1 2
dx
, yn )
3.
Численные методы решения дифференциальныхуравнений
y1
f1
y
f
Y 2
F 2
y
f
n
n
dY
F ( x,Y ( x ))
dx
Y Y ( x, C )
c1
c
C 2
c
n
4.
Виды задач для ОДУ• Задача Коши
• Краевая задача
• Задача на собственные значения
5.
Методы решения ОДУАналитические методы
Графические методы
Приближенные методы
Численные методы
6.
Особенности численных методов решенияОДУ
dY
F ( x,Y ( x ))
dx
x [ x0 ; xn ]
7.
Хорошо обусловленные задачиdy
y x
dx
0 x 100
y ( x0 ) 1
y ( x, c ) 1 x ce
x
y (0) 1
c 0
y (100) 101
y (0) 1.000001
c 10 6
y (100) 2.7 1037
8.
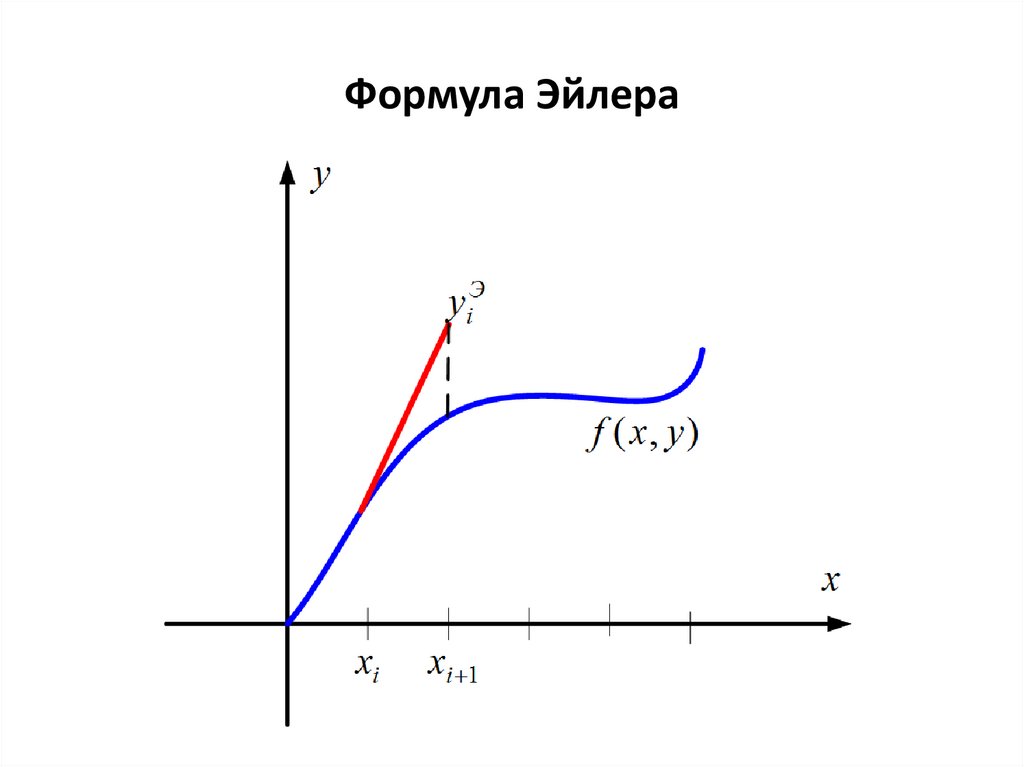
Метод (формула) Эйлераdy
f ( x, y )
dx
x [ x0 ; xn ]
y ( x0 ) y0
xn x0
h
n
xi 1 xi h
yi 1 yi hf ( xi , yi )
9.
Формула Эйлера10.
Формула Эйлераdy
0.9 x y
dx
x [0;0.2] h 0.1
y (0) 1
x0 0
y0 1
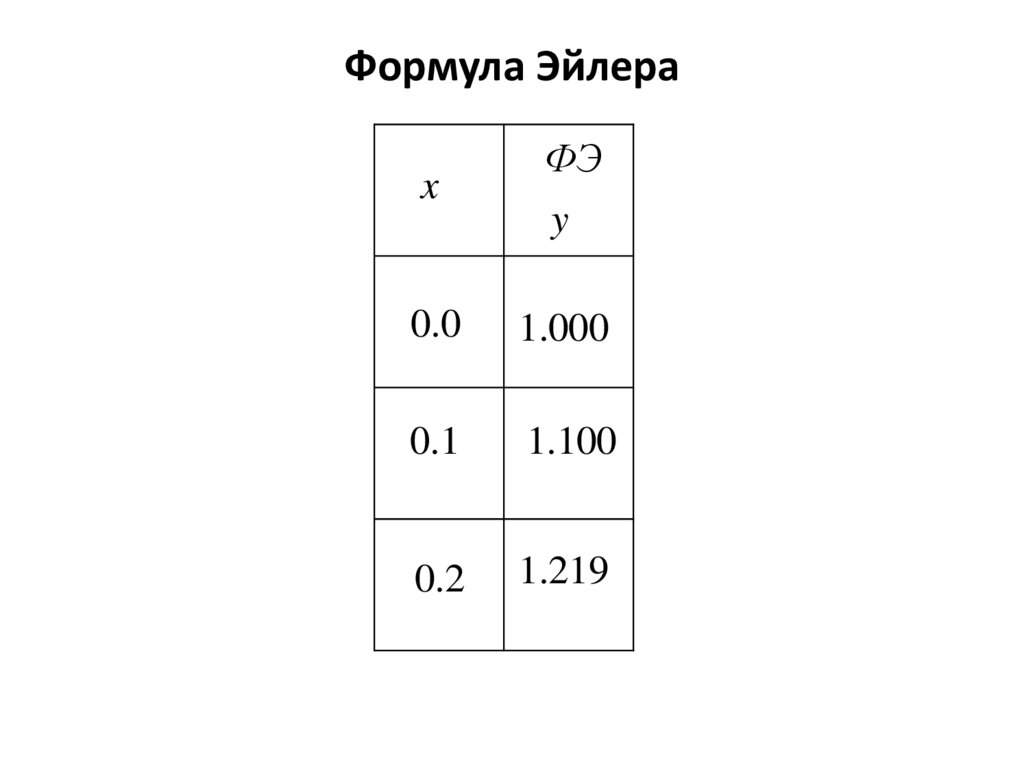
x1 x0 h 0 0.1 0.1
y1 y0 hf ( x0 , y0 ) 1 0.1 (0.9 0 1) 1.100
x2 x1 h 0.1 0.1 0.2
y2 y1 hf ( x1 , y1 ) 1.1 0.1 (0.9 0.1 1.1) 1.219
11.
Формула Эйлераx
ФЭ
y
0.0
1.000
0.1
1.100
0.2
1.219
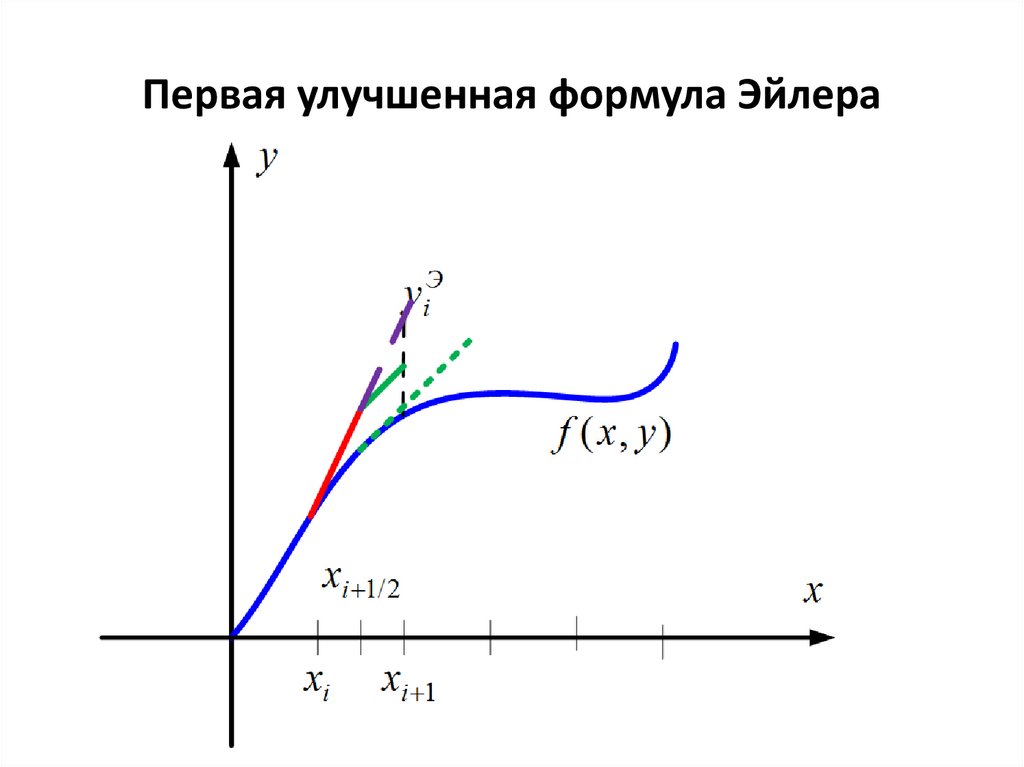
12.
Первая улучшенная формула Эйлера13.
Первая улучшенная формула Эйлераx [ x0 ; xn ]
промежуточная точка
xi 1/2 xi h / 2
yi 1/2
h
yi f ( xi , yi )
2
xi 1 xi h
yi 1 yi hf ( xi 1/2 , yi 1/2 )
14.
Первая улучшенная формула Эйлераdy
0.9 x y
dx
x [0;0.2] h 0.1
y (0) 1
x0 0
y0 1
h
0.1
x0 1/2 x0 0
0.05
2
2
h
0.1
y0 1/2 y0 f ( x0 , y0 ) 1
(0.9 0 1) 1.050
2
2
x1 x0 h 0 0.1 0.1
y1 y0 hf ( x0 1/2 , y0 1/2 ) 1 0.1 (0.9 0.05 1.050) 1.110
15.
Первая улучшенная формула Эйлераh
0.1
x1 1/2 x1 0.1
0.15
2
2
h
y1 1/2 y1 f ( x1 , y1 )
2
0.1
1.110
(0.9 0.1 1.110) 1.170
2
x2 x1 h 0.1 0.1 0.2
y2 y1 hf ( x1 1/2 , y1 1/2 )
1.110 0.1 (0.9 0.15 1.170) 1.240
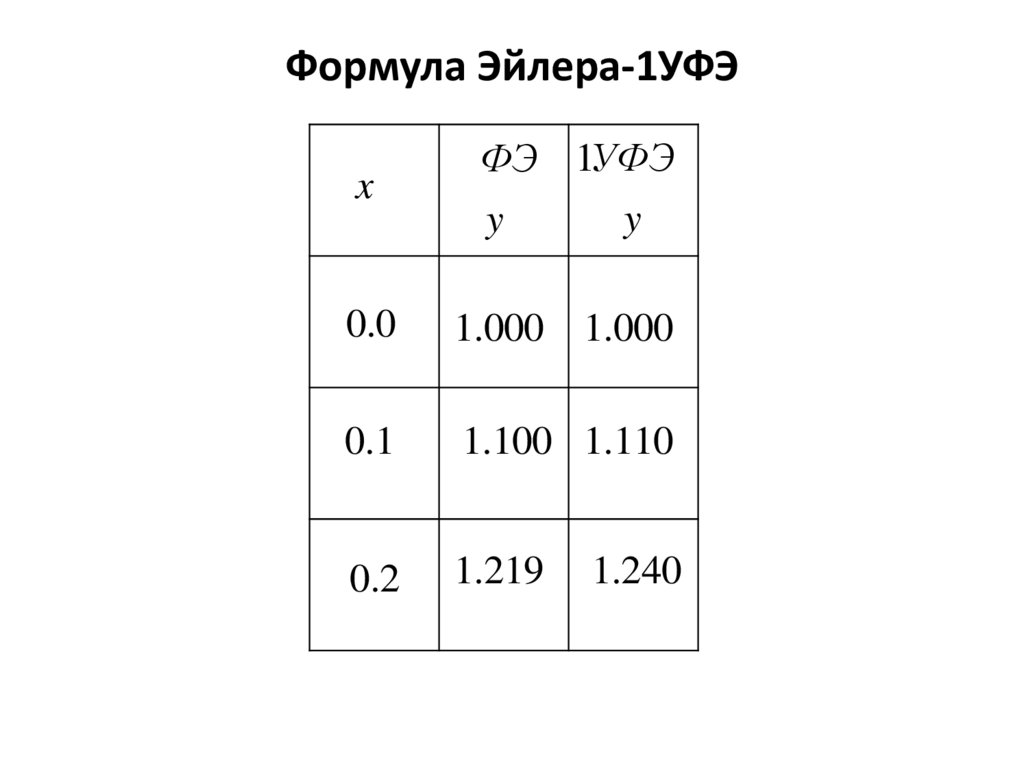
16.
Формула Эйлера-1УФЭx
ФЭ 1УФЭ
y
y
0.0
1.000 1.000
0.1
1.100 1.110
0.2
1.219
1.240
17.
Вторая улучшенная формула Эйлераx [ x0 ; xn ]
промежуточная точка
xi* xi h
yi* yi hf ( xi , yi )
xi 1 xi h
f ( xi , yi ) f ( xi* 1 , yi* 1 )
yi 1 yi h
2
18.
Вторая улучшенная формула Эйлераdy
0.9 x y
dx
y (0) 1
x0 0
x [0;0.2] h 0.1
y0 1
x1 x0 h 0 0.1 0.1
*
y1* y0 hf ( x0 , y0 ) 1 0.1 (0.9 0 1) 1.100
x1 x0 h 0 0.1 0.1
f ( x0 , y0 ) f ( x1* , y1* )
y1 y0 h
2
(0.9 0 1) (0.9 0.1 1.1)
1 0.1
1.110
19.
Вторая улучшенная формула Эйлераx2* x1 h 0.1 0.1 0.2
y2* y1 hf ( x1 , y1 )
1.110 0.1 (0.9 0.2 1.110) 1.239
x2 x1 h 0.1 0.1 0.2
f ( x1 , y1 ) f ( x2* , y2* )
y2 y1 h
2
(0.9 0.1 1.110) (0.9 0.2 1.239)
1.110 0.1
1.241
2
20.
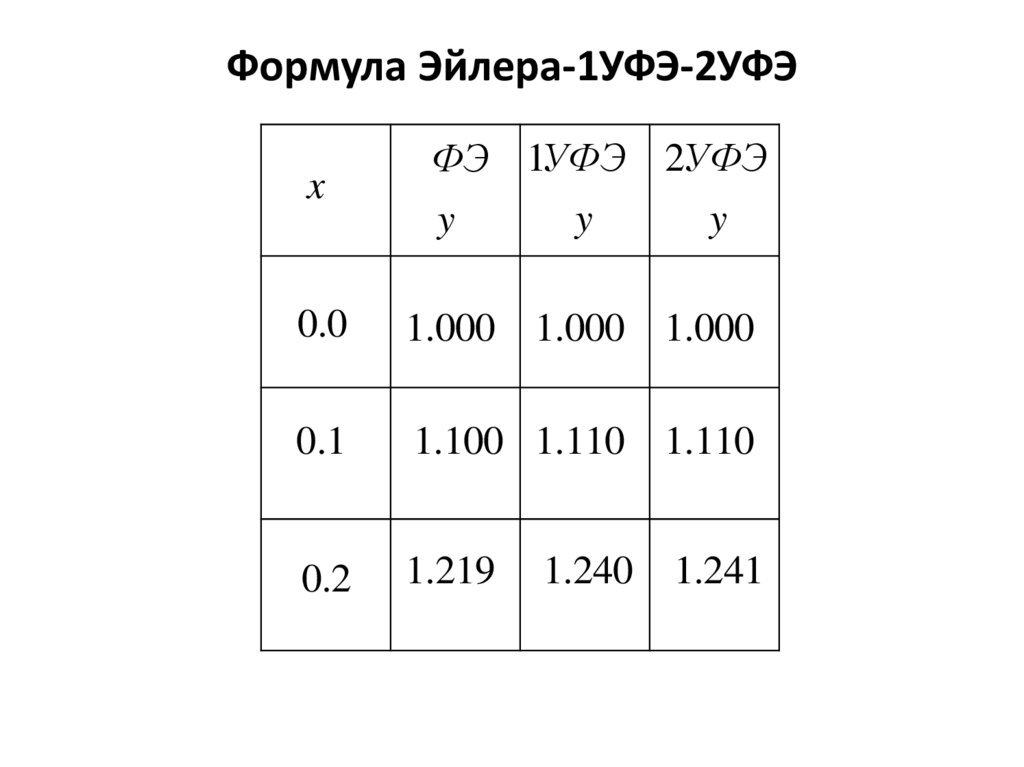
Формула Эйлера-1УФЭ-2УФЭx
ФЭ 1УФЭ 2УФЭ
y
y
y
0.0
1.000 1.000 1.000
0.1
1.100 1.110 1.110
0.2
1.219
1.240
1.241
21.
Обобщенная формула Рунге-Куттаk1 hf ( xi , yi )
k2 hf ( xi 2 h, yi 21k1 )
k s hf ( xi s h, yi s1k1
xi 1 xi h
s
yi 1 yi m km
m 1
22.
Формула Рунге-Кутта 4-го порядкаk1 hf ( xi , yi )
k1
h
k2 hf ( xi , yi )
2
2
k2
h
k3 hf ( xi , yi )
2
2
k4 hf ( xi h, yi k3 )
xi 1 xi h
k1 2(k2 k3 ) k4
yi 1 yi
6
23.
k1 hf ( x0 , y0 ) 0.1 (0.9 0 1) 0.1h
k1
0.1
0.1
k2 hf ( x0 , y0 ) 0.1 (0.9 (0
) (1
) 0.110
2
2
2
2
h
k2
0.1
0.11
k3 hf ( x0 , y0 ) 0.1 (0.9 (0
) (1
) 0.110
2
2
2
2
k4 hf ( x0 h, y0 k3 ) 0.1 (0.9 (0 0.1) (1 0.110) 0.120
x1 x0 h 0 0.1 0.1
k1 2(k2 k3 ) k4
y1 y0
6
0.1 2(0.110 0.110) 0.12
1
1.110
6
24.
k1 hf ( x1 , y1 ) 0.1 (0.9 0.1 1.11) 0.120h
k1
k2 hf ( x1 , y1 )
2
2
0.1
0.12
0.1 (0.9 (0.1
) (1.11
) 0.130
2
2
h
k2
k3 hf ( x1 , y1 )
2
2
0.1
0.13
0.1 (0.9 (0.1
) (1.11
) 0.131
2
2
k4 hf ( x1 h, y1 k3 ) 0.1 (0.9 (0.1 0.1) (1 0.131) 0.142
x2 x1 h 0 0.1 0.1
k1 2(k2 k3 ) k4
y2 y1
6
0.12 2(0.130 0.131) 0.142
1.11
1.241
6
25.
Формула Эйлера-1УФЭ-2УФЭ-формулаРунге-Кутта
ФЭ 1УФЭ 2УФЭ
y
y
y
ФРК
0.0
1.000 1.000 1.000
1.000
0.1
1.100 1.110 1.110 1.110
0.2
1.219
x
1.239 1.241
y
1.241
26.
Выбор шага интегрирования в формулеРунге-Кутта 4-го порядка
i
k2
i
k1
i
k3
i
k4
0.01 0.03

















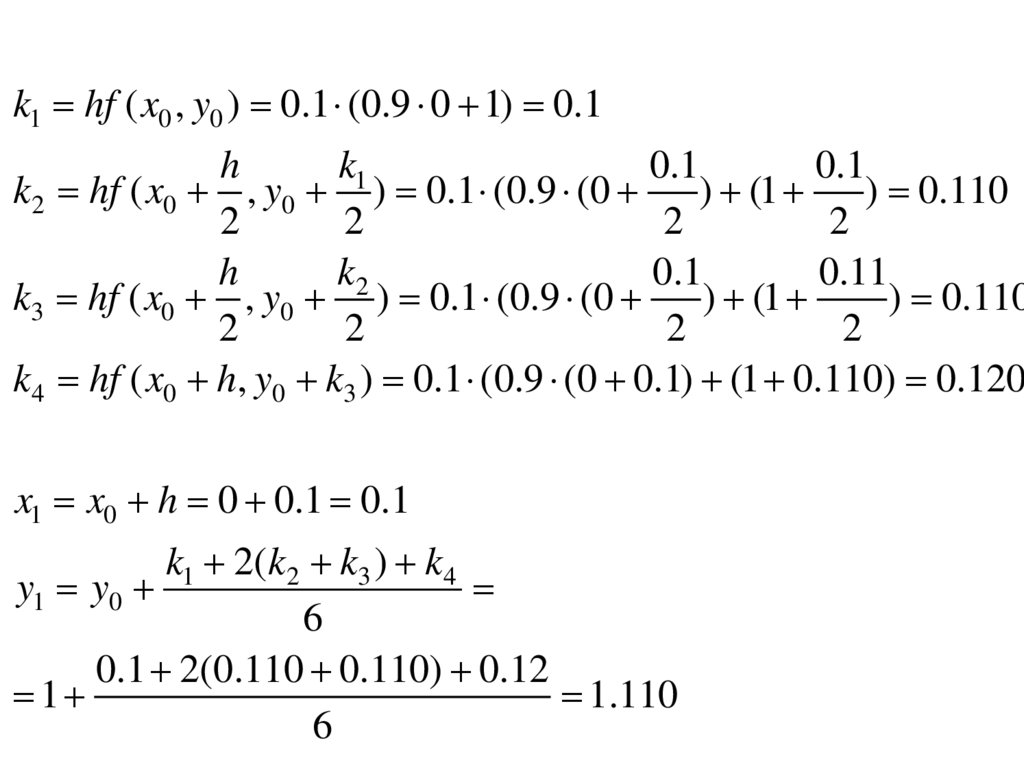
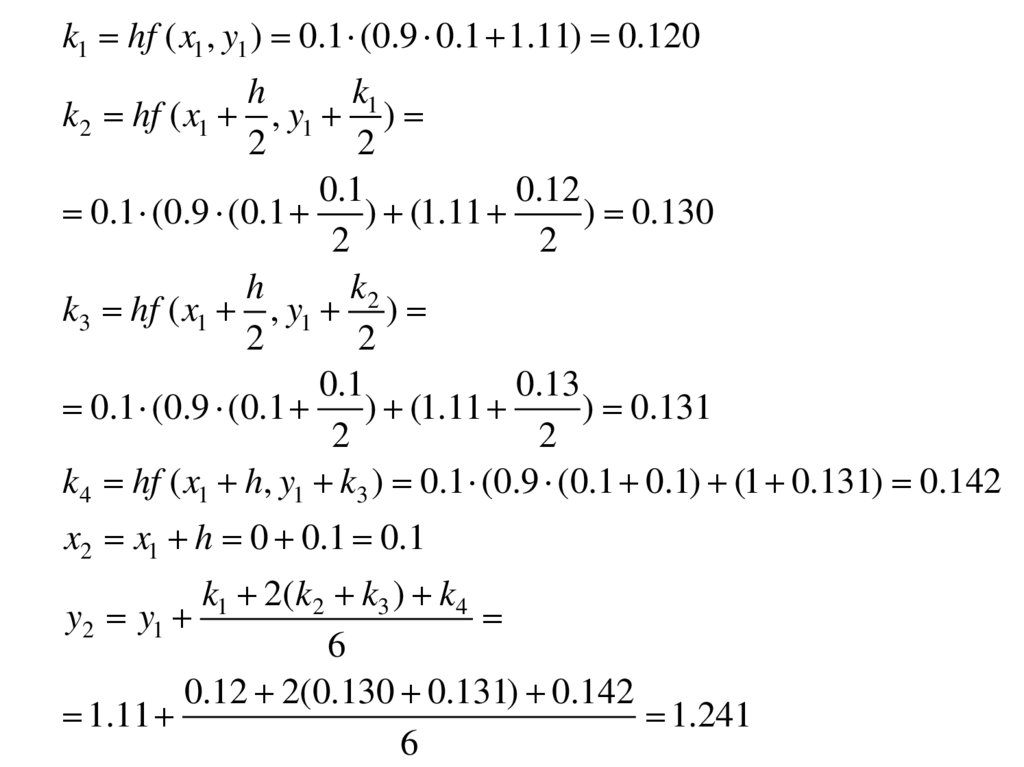


 mathematics
mathematics








