Численные методы решения дифференциальных уравнений. Лекция 2

1.

Лекция 2
1.
2.
3.
4.
5.
Список литературы
Охорзин В.А.
Прикладная математика в системе Mathcad
Демидович Б.П., Марон И.А. Основы вычислительной
математики
Самарский А.А., Гулин А.В. Численные методы
Кремер Н.Ш. Теория вероятностей и математическая статистика
Компьютерное моделирование. №6401 (ВГАУ)
Численные методы решения дифференциальных уравнений
1.Понятие о методе Эйлера (геометрическая интерпретация)
2. Особенности реализации метода Эйлера в системе Mathcad
3. Усовершенствованный метод ломаных
4.Метод Эйлера-Коши
5.Аппроксимация производных разностными отношениями. Порядок
аппроксимации
6. Явная и неявная схемы Эйлера
7. Методы Рунге-Кутта и их реализация в системе Mathcad

2.

1.Понятие о методе Эйлера (геометрическая интерпретация)
Решение начальных задач с дифференциальными уравнениями является
необходимым этапом математического моделирования. Приближенные
решения можно получить с помощью методов, основанных на методе Эйлера.
Рассмотрим начальную задачу
y f ( x, y)
x a, b
(1.1)
y (a) y 0
Метод Эйлера заключается в следующем.
Отрезок
a, b
точками
a x0 , x1 ,..., xN b
мелких и равных частей длины
h
разбивается на
N
b a
N
Дифференциальной задаче (1.1) соответствует разностная задача
vi vi 1
f ( xi 1 , vi 1 ),
h
i 1,..., N
x0 a
xi xi 1 h
v0 y 0
(1.2)

3.

Систему уравнений называют явной схемой Эйлера. Эта система приводится к
рекуррентным формулам
x0 a
v0 y 0
xi xi 1 h
vi vi 1 h f ( xi 1 , vi 1 )
i 1,..., N
При изучении свойств метода Эйлера полезно рассмотреть геометрическую
интерпретацию этого метода.
Дифференциальное уравнение первого порядка определяет поле направлений на плоскости: в каждой точке плоскости определена
касательная к интегральной кривой, проходящей через данную точку.
Угловой коэффициент касательной определяется по формуле
k tg y f x, y
k f ( x, y)
Метод Эйлера состоит в том, что касательные, образующие ломаную Эйлера,
проводятся к различным интегральным кривым дифференциального уравнения.
При некоторых значениях шага интегрирования приближенное решение
(ломаная Эйлера) существенно отклоняется от точного решения задачи. Данное
свойство получило название неустойчивости разностной схемы.

4.

,
.
vi vi 1
tg i 1 f xi 1 , vi 1
h

5.

2. Особенности реализации метода Эйлера в системе Mathcad
Рассмотрим задачу
x
y
y
y 2 4
x 2;10
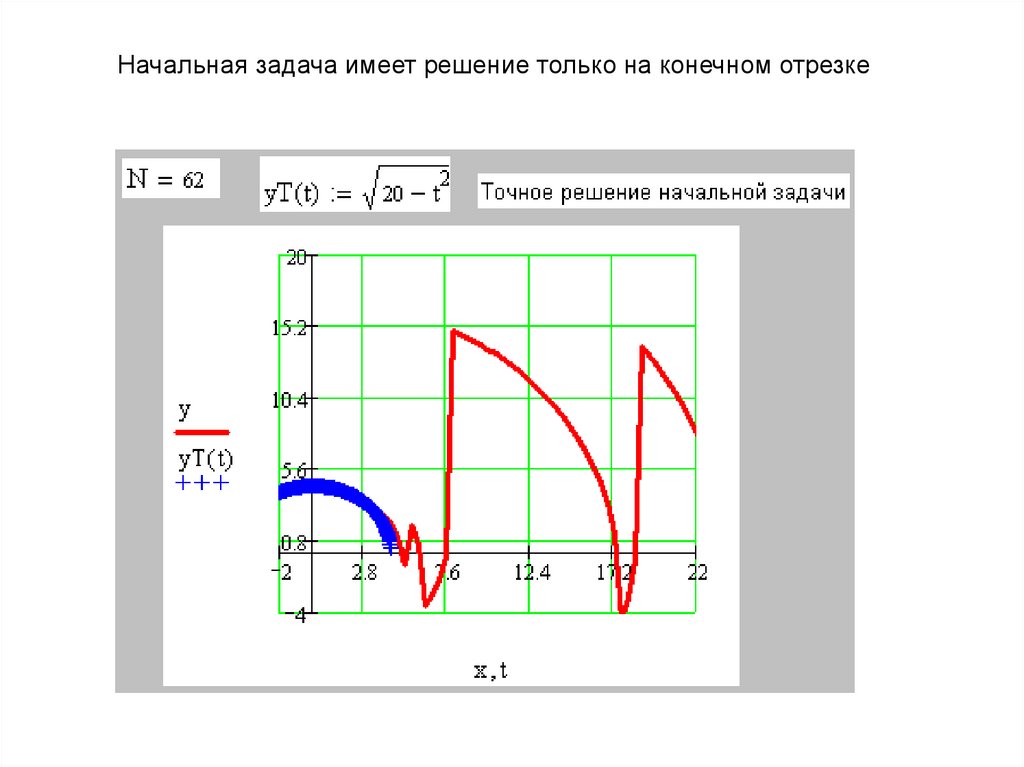
Точное решение задачи имеет вид
Построим поле направлений дифференциального уравнения
y 20 x 2
y
x
y

6.

V0 4
xi xi 1 h
Vi Vi 1 h
xi 1
Vi 1
h
10 ( 2)
N
N 12
i 1,...,100

7.

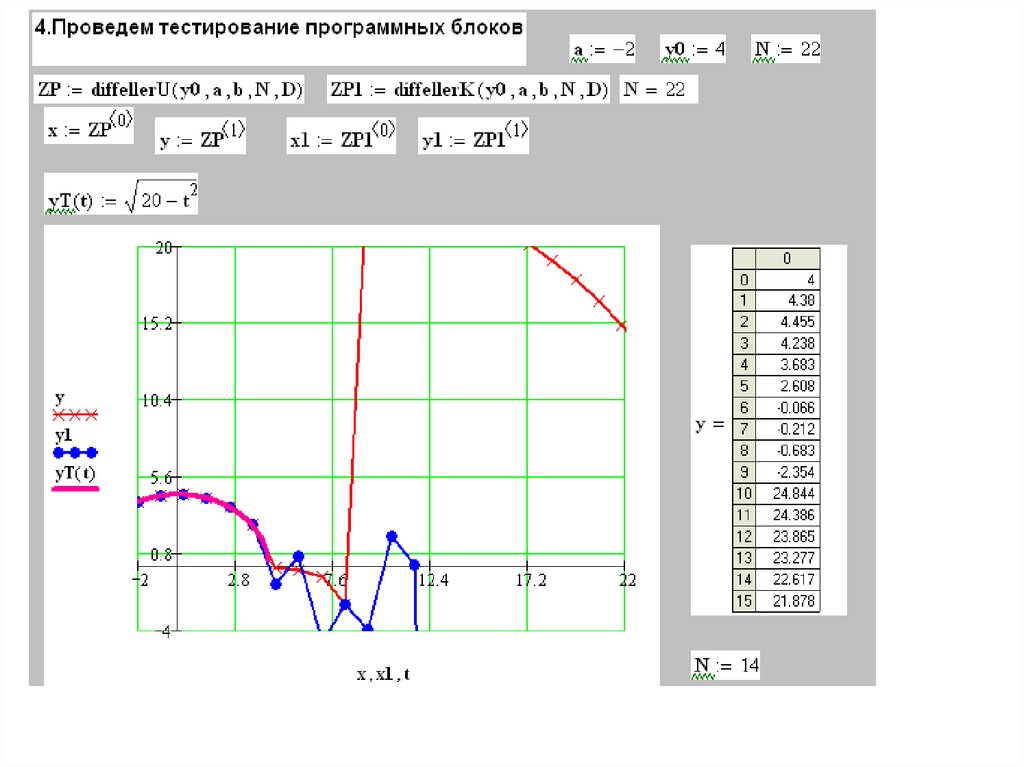
Реализация явной схемы Эйлера в системе Mathcad

8.

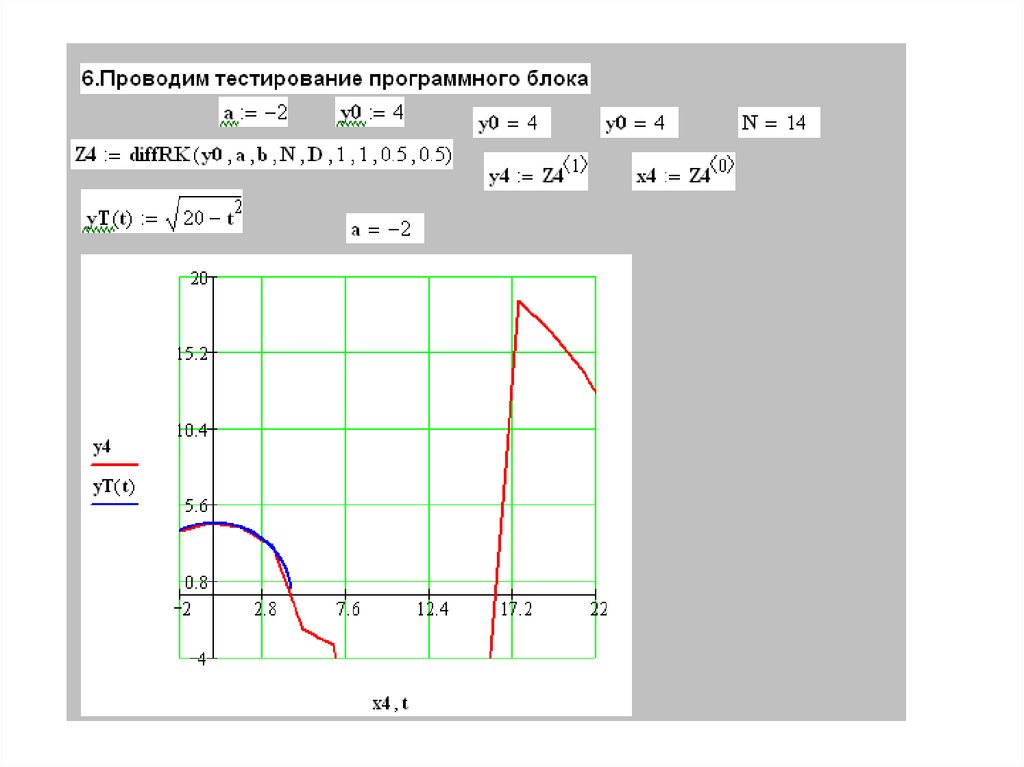
Начальная задача имеет решение только на конечном отрезке

9.

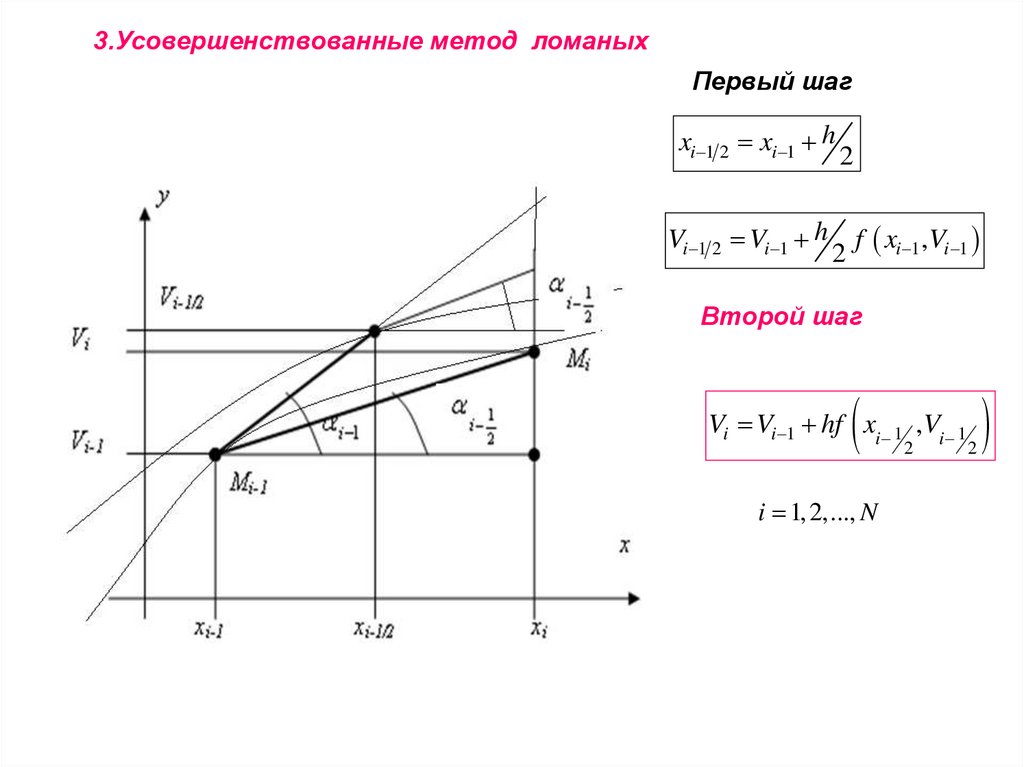
3.Усовершенствованные метод ломаных
Первый шаг
xi 1 2 xi 1 h
Vi 1 2 Vi 1 h
2
2
f xi 1 ,Vi 1
Второй шаг
Vi Vi 1 hf xi 1 ,Vi 1
i 1, 2,..., N
2
2

10.

11.

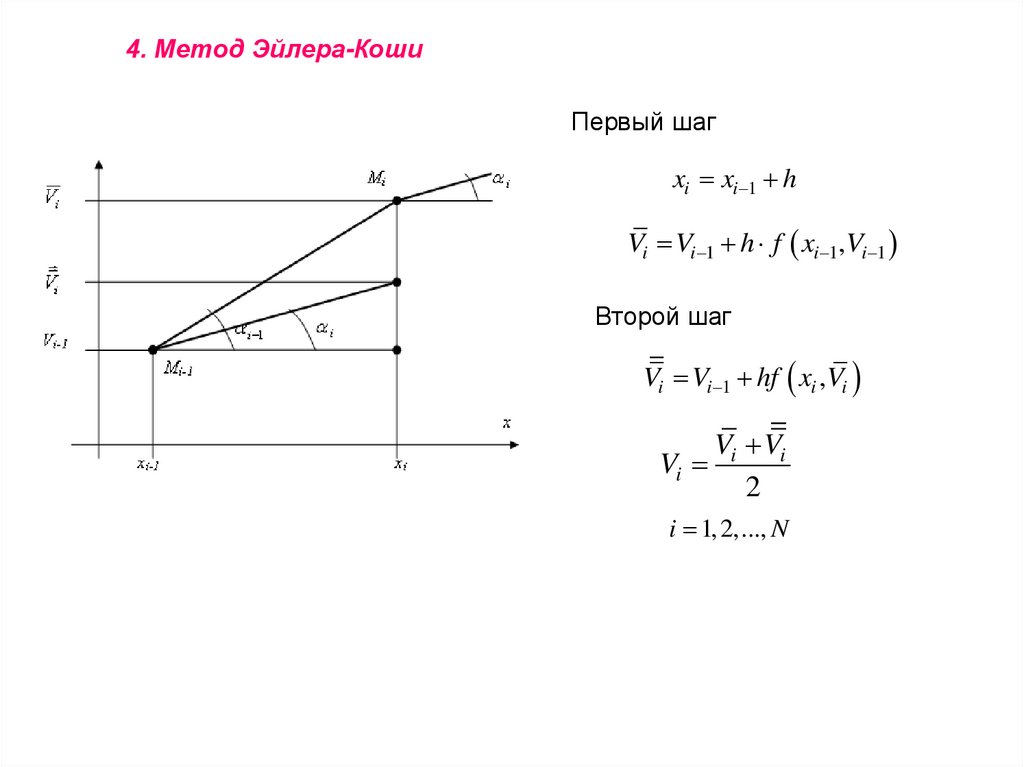
4. Метод Эйлера-Коши
Первый шаг
xi xi 1 h
Vi Vi 1 h f xi 1,Vi 1
Второй шаг
Vi Vi 1 hf xi ,Vi
Vi Vi
Vi
2
i 1, 2,..., N

12.

13.

14.

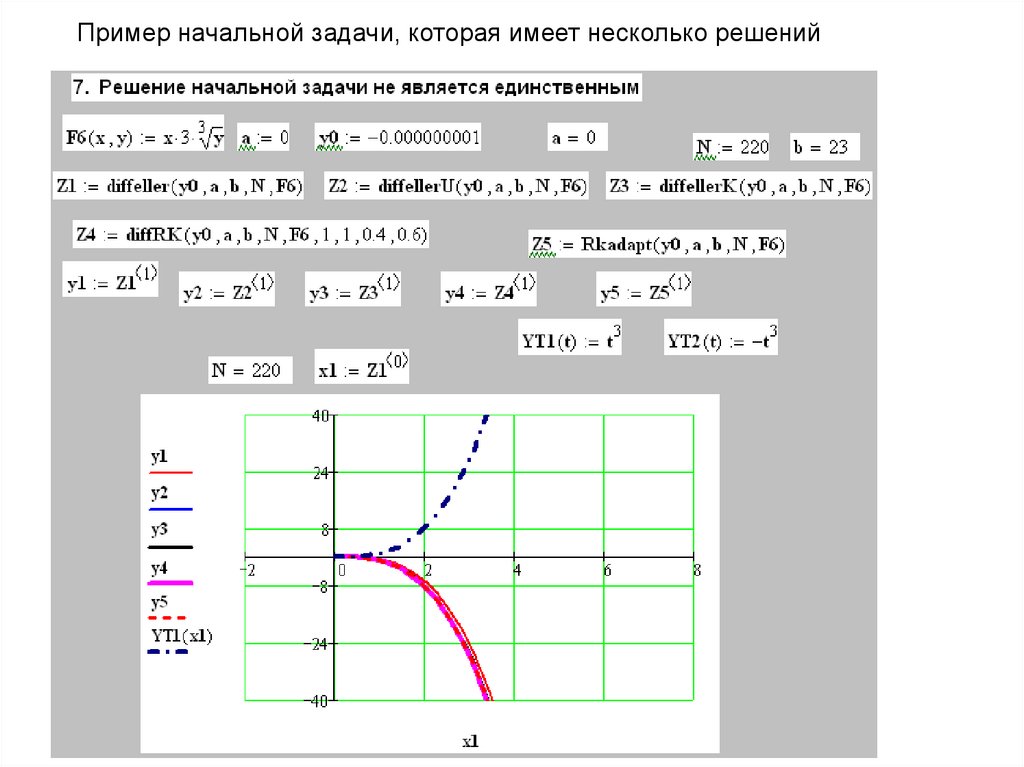
Пример начальной задачи, которая имеет несколько решений

15.

5.Аппроксимация производных разностными отношениями. Порядок
аппроксимации
Сеткой на отрезке [a, b] называют любое конечное множество точек
этого отрезка
x
x0=a
x1
xi-1
xi
xi+1
b=xN
Функция, определенная в точках сетки, называется сеточной функцией
h xi a ih, i 1,..., N 1
Пусть
где
h
b a
N
- шаг сетки, точка
- равномерная сетка на [a, b]
хi – узел сетки
Рассмотрим функцию y(x), которая имеет производные некоторого
порядка
yi y xi С учетом принятого обозначения
Введем обозначения
y y
- правая разностная производная в точке хi
y x i 1 i
h
y yi 1
- левая разностная производная в точке хi
yx i
h
yi 1 yi 1
y xˆ
- центральная разностная производная в точке хi
2h

16.

Рассмотрим погрешность замены производной разностными
отношениями (погрешность аппроксимации)
Формула Тейлора в форме Лагранжа имеет вид
f x f x0
f x0
1!
x x0
x x0 , x0
f x0
2!
x x0
2
...
n
f x0
n!
x x0
f x
n 1
x
x
0
n 1 !
n 1
n
x x0 , x
Бесконечно малая величина называется бесконечно малой порядка k
по отношению к бесконечно малой
одного порядка:
lim k A 0
α,
если и
Записывают
к есть бесконечно малые
O k
Локальная формула Тейлора имеет вид
f x f x0
f x0
1!
x x0
f x0
2!
x x0
2
...
n
f x0
n!
x x0
n
O x x0
n 1

17.

Пусть функция
y y x
x xi h
тогда
обладает необходимой гладкостью
и в точке xi
h2
y xi h y xi y xi h y xi O h3
2!
Отсюда получаем
y xi h y xi
h
y xi O h
y xi h y xi
y xi O h
h
h2
y xi h y xi y xi h y xi O h3
2!
y xi y xi h
h
y xi O h
y xi y xi h
y xi O h
h
Разностные отношения аппроксимируют производные с первым
порядком относительно h

18.

h2
y xi h y xi y xi h y xi O h3
2!
h2
y xi h y xi y xi h y xi O h3
2!
y xi h y( xi h) 2 y xi h O h3
y xi h y ( xi h)
2h
y xi O h
2
y xi h y xi h
y xi O h 2
2h
Центральное разностное отношение аппроксимирует производную
со вторым порядком
Замечание. В дальнейшем используются обозначения.
yi y xi
yi 1 y xi h
yi 1 y xi h

19.

6. Явная и неявная схемы Эйлера
du
f x, u
dx
u a u0
x a, b
yi yi 1
f xi 1 , yi 1 - явная схема Эйлера
h
yi yi 1
f xi , yi - неявная схема Эйлера
h
Метод (численный) сходится в точке
yi u xi 0
xi ih x , если
при
h 0
Говорят, что метод имеет
порядок точности p, если
существует p > 0, такое, что
yi u xi O h p
при
h 0

20.

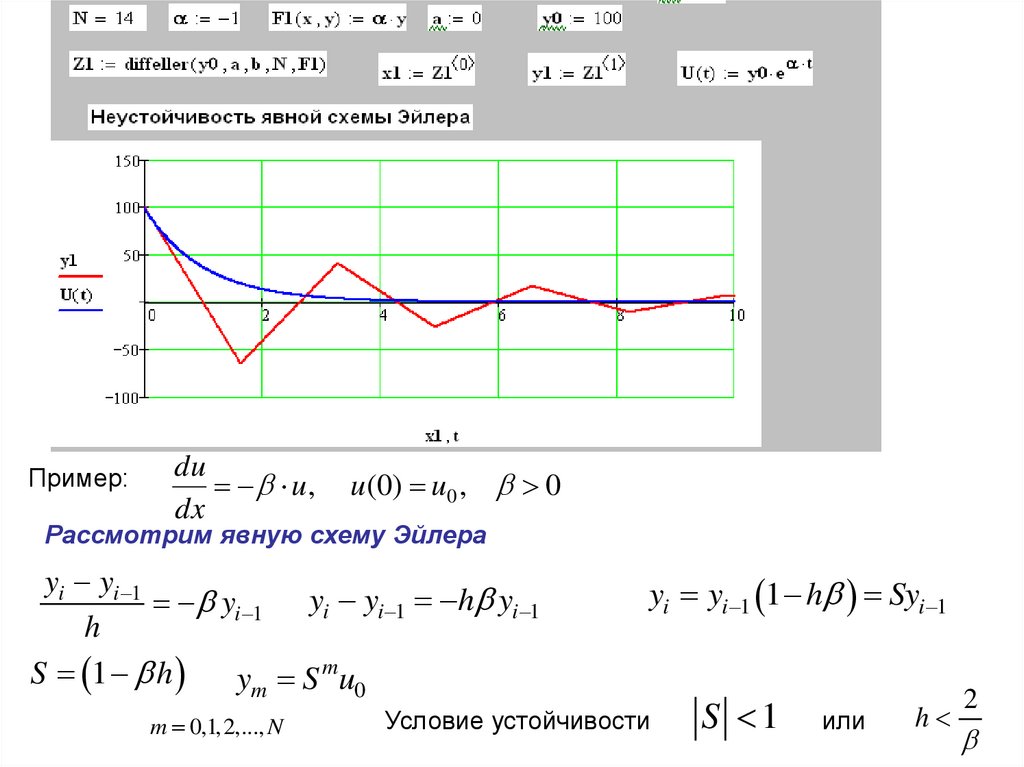
Пример:
du
u,
dx
u (0) u0 , 0
Рассмотрим явную схему Эйлера
yi yi 1
yi 1 yi yi 1 h yi 1
h
S 1 h
ym S mu0
m 0,1,2,..., N
yi yi 1 1 h Syi 1
Условие устойчивости
S 1
или
h
2

21.

Неявная схема Эйлера
yi yi 1
yi
h
yi yi 1 h yi
yi 1 h yi 1
Отсюда следует
ym
u0
1 h
m
m 0,1,2,..., N
При любом h значения ym уменьшаются с ростом m. Это
соответствует убыванию точного решения начальной задачи.
Неявная схема является абсолютно устойчивой.

22.

7. Методы Рунге-Кутта и их реализация в системе Mathcad
k1 f xi 1, yi 1
k2 f xi 1 a2 h, yi 1 b21 h k1
yi yi 1 h 1k1 2k2
Схема Эйлера - Коши
a2 b21 1
1 2
1
2