Similar presentations:
Численное решение обыкновенных дифференциальных уравнений. Лекция 6
1.
ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
В основе численных методов решения ОДУ лежит
замена исходного уравнения его дискретным
аналогом – разностным уравнением.
При этом область непрерывного изменения аргумента
заменяется дискретным множеством точек (узлами):
x xk. Узлы составляют разностную сетку.
Искомая функция непрерывного аргумента приближенно
заменяется функцией дискретного аргумента на
заданной сетке: y yk. Эта функция называется
сеточной функцией.
Она определена только в узлах разностной сетки.
1
2.
ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Исходное дифференциальное уравнение приближенно
заменяется разностным уравнением относительно
сеточной функции:
Ly = f(x,y) Lkyk = f(xk,yk),
где L – дифференциальный оператор, Lk – разностный
оператор.
При этом производные заменяются по известным нам
формулам численного дифференцирования. Такая
замена дифференциального уравнения на разностное
называется аппроксимацией.
Граничные условия также заменяются их разностными
аналогами.
2
3.
ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Совокупность разностных уравнений,
аппроксимирующих исходное дифференциальное
уравнение или систему дифференциальных уравнений и
дополнительные условия на границах, называется
разностной схемой.
Решение разностной задачи, в результате которого
находятся значения сеточной функции yk в узлах xk ,
приближенно заменяет решение y(x) исходной
дифференциальной задачи.
Не всякая разностная схема дает удовлетворительное
решение!!!
3
4.
ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
К разностной схеме предъявляются определенные
требования, касающиеся устойчивости,
аппроксимации и сходимости разностной схемы.
Разностная схема называется устойчивой, если на
каждом шаге счета любая ошибка не возрастает при
переходе от одного шага к другому.
Разностное уравнение аппроксимирует дифференциальное уравнение, если погрешность аппроксимации
стремится к нулю при измельчении сетки.
Погрешность аппроксимации – это разность между
дифференциальным уравнением и его разностным
аналогом.
4
5.
ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Если решение существует, единственно и если схема
устойчива, то разностная схема называется корректной.
Пусть k – разница между значениями сеточной функции и
искомой функции в узле сетки xk, т.е. k = yk – y(xk).
Тогда
yk = y(xk) + k .
Подставляем в разностное уравнение:
Lky(xk) + Lk k = fk (xk, yk).
Здесь Lk k = Rk – погрешность аппроксимации.
Если Rk = O(hp), то разностная схема имеет p-ый порядок
аппроксимации.
5
6.
ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Если yk y(xk) или =max( k) 0 при h 0, то говорят, что
разностная схема сходится (т.е. решение разностной
задачи сходится к решению дифференциальной задачи)
Теорема Лакса
Если имеется корректно поставленная линейная
задача с начальными условиями и конечно разностное
уравнение аппроксимирует исходное
дифференциальное уравнение, то устойчивость
является необходимым и достаточным условием
сходимости.
Справедлива для некоторого класса линейных задач.
6
7.
ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Краткая формулировка теоремы Лакса
аппроксимация + устойчивость = сходимость.
Для нелинейных же задач эта теорема не всегда строго
применима, так что в этом случае правильнее говорить
только о необходимых условиях сходимости.
Многолетняя практика использования численных
методов для решения практических задач на ЭВМ
показывает, что применение той или иной разностной
схемы, даже если она исследована теоретически,
требует её тщательной апробации при решении
конкретной задачи !!!
7
8.
РАЗНОСТНАЯ СХЕМА ЭЙЛЕРАРассмотрим задачу Коши:
dy
f (x, y);
dx
y a y0 .
Отрезок [a,b] делим N узлами на шаги:
h = xk+1 – xk = (b – a)/N.
Метод Эйлера основан на разложении искомой
функции y(x) в ряд Тейлора в окрестностях узлов хk :
y(xk + h) = y(xk) +y'(xk)h +o(h2).
Вместо искомой функции y(хk) будем рассматривать
сеточную функцию yk, определенную в узлах сетки.
8
9.
РАЗНОСТНАЯ СХЕМА ЭЙЛЕРАЗаменяем значения функции y(xk) и y(xk+1) значениями
сеточной функции yk , yk+1 и отбрасываем все члены,
содержащие производные второго и более высоких
порядков :
yk+1 = yk + y'(xk) h.
Поскольку d y f (x, y) , то y'(xk) = f(xk,, yk).
dx
Следовательно
yk+1 = yk +hf(xk, yk).
Это есть формула метода Эйлера.
Локальная погрешность схемы Эйлера (ошибка на
~
одном шаге) равна R o(h 2 ).
9
10.
РАЗНОСТНАЯ СХЕМА ЭЙЛЕРАКаков алгоритм получения численного решения?
1) Задаем x0, y0;
2) Находим y1 = y0 +hf(x0, y0);
3) Находим y2 = y1 +hf(x1, y1);
4) И т.д.
5) Находим yN = yN - 1 +hf(xN - 1, yN - 1);
Поскольку по известным значениям xk и yk находим
новое значение yk+1 , то метод называют одношаговым.
Метод Эйлера является одношаговым.
10
11.
РАЗНОСТНАЯ СХЕМА ЭЙЛЕРАКакой порядок аппроксимации имеет схема Эйлера?
По определению Rk = fk – Lk y(xk).
Тогда
y ( xk 1 ) y ( xk )
Rk f k
f k y ' ( xk ) o ( h ) o ( h )
h
Это означает, что схема Эйлера имеет первый порядок
аппроксимации.
Покажем сходимость схемы Эйлера, что означает
max k 0 при h 0.
k
Покажем, что сходимость схемы Эйлера имеет первый
порядок точности, т.е.
o(h).
11
12.
РАЗНОСТНАЯ СХЕМА ЭЙЛЕРАПредположим, что следующие функции ограничены
f M 1 ; f 'x M 2 ; f ' y M 3.
Из этих ограничений вытекает следующее:
|y″| = |f′x + f′yy′x| M2 +M3 M1 = M4.
Рассмотрим разность между значением сеточной
функции и искомой функции в точках xk+1,
k 1 yk 1 y(xk 1)
h2
yk hf (xk , yk ) y(xk ) y' (xk )h
y" (xk )
2
h2
k h f (xk , yk ) f (xk , y (xk )) y" (xk )
2
12
13.
РАЗНОСТНАЯ СХЕМА ЭЙЛЕРАh2
k h f (xk , yk ) f (xk , yk k ) y" (xk )
2
2
k hf y k o(h )
или
k h M 3 k o(h2 )
k 1 1 hM3 k o(h 2 )
Введем обозначение c = 1+hM3, тогда
k 1 c k o(h2 )
13
14.
РАЗНОСТНАЯ СХЕМА ЭЙЛЕРАЗапишем неравенства для разных k.
k c k 1 o(h )
2
k 1 c k 2 o(h )
2
1 c 0 o(h )
2
Выразим k через 0 :
k c2 k–2 + с o(h2) + o(h2)
c3 k–3 + с2 o(h2) + c o(h2) + o(h2) …
… ck 0 + сk–1o(h2) + сk–2o(h2) +…+ c o(h2) + o(h2).
14
15.
РАЗНОСТНАЯ СХЕМА ЭЙЛЕРАОшибка N в конечной точке интервала будет
содержать сумму N членов с множителями вида
ck o(h2), т.е.
N cN 0 + N O(h2)=
b a
N
c 0
O(h2 )=
h
=cN 0 + O(h).
Таким образом, если начальные данные заданы
точно (т.е. 0=0), то при h 0 значение 0 и =O(h),
т.е. разностная схема Эйлера обеспечивает
сходимость с первым порядком точности.
15
16.
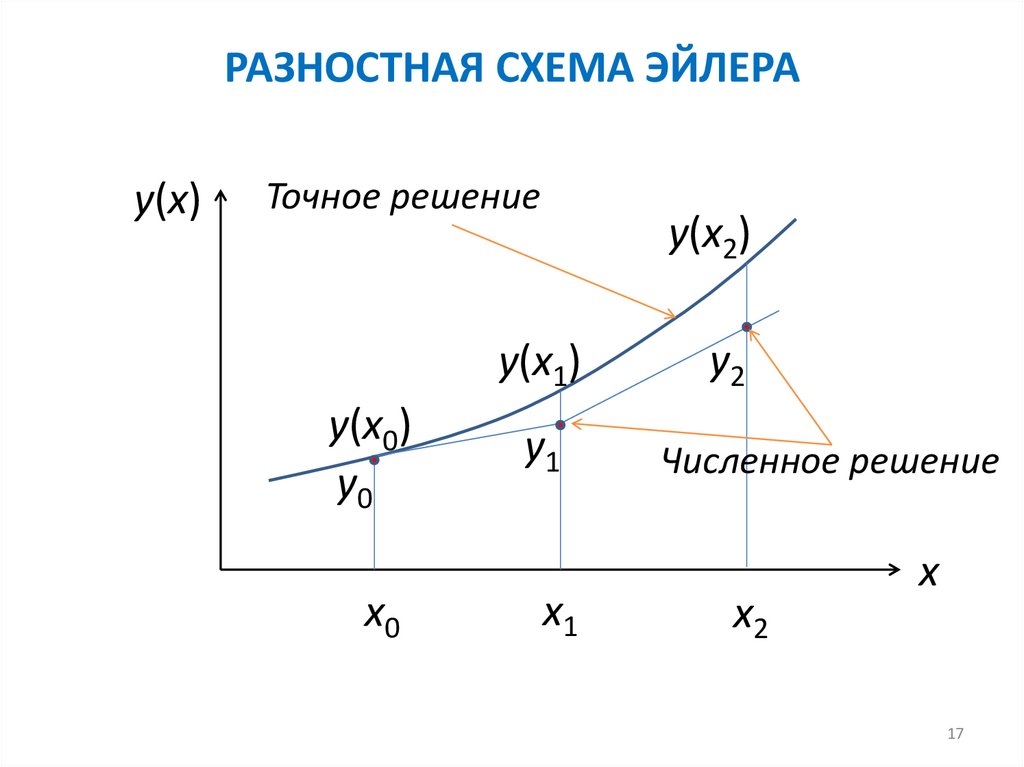
РАЗНОСТНАЯ СХЕМА ЭЙЛЕРАГеометрический смысл схемы Эйлера.
Уравнения касательной к функции y(x) в точке х0
y y0 (x x0 ) y (x0 ).
В качестве х возьмем точку х1 , тогда
y1 y0 (x1 x0 ) y (x0 ).
Т.к. y x0 f (x0 , y0 ) , то y1 y0 (x1 x0 ) f (x0 ,y0 ).
А схема Эйлера имеет вид: y1 y0 hf ( x0 , y0 )
Т.е. геометрический смысл схемы Эйлера заключается в
замене функции y(x) на отрезке [хk, хk+1] отрезком
касательной, проведенной к графику в точке хk
16
17.
РАЗНОСТНАЯ СХЕМА ЭЙЛЕРАy(x)
Точное решение
y(x2)
y(x1)
y(x0)
y0
x0
y1
x1
y2
Численное решение
x2
x
17
18.
МЕТОДЫ РУНГЕ-КУТТАМетод Эйлера является частным случаем «методов
Рунге-Кутта».
Свойства методов Рунге-Кутта:
1) они являются одношаговыми, т.е. чтобы найти yk+1,
нужна информация только о предыдущей точке: xk, yk, и
явными (явная зависимость yk+1 от yk);
2) они имеют порядок hp, где p – степень порядка
(различна для различных методов);
3) они требуют только вычисления самой функции f(x,y),
а не ее производных.
18
19.
МЕТОДЫ РУНГЕ-КУТТАВсе методы Рунге-Кутта можно представить в виде:
yk+1 = yk + h (xk, yk)
Для метода Эйлера функцией является сама функция f.
Рассмотрим функцию , определяемую соотношением
(x,y) = c2f(x,y) + c3f(x+c1h, y+c1hf(x,y)).
Найдем такие значения коэффициентов с1, с2 и с3, чтобы
порядок метода был максимальным.
Согласно определению погрешности аппроксимации
R = c2f(x,y) + c3f(x+c1h, y+c1hf(x,y)) – y ( x h) y ( x) h
19
20.
МЕТОДЫ РУНГЕ-КУТТА1. Разложим функцию в ряд Тейлора по двум
переменным в окрестности точки (x, y): сначала по х, а
затем по у.
(x,y) = c2f(x,y)+c3{f(x,y+c1hf)+с1hfx′(x,y+c1hf)+
+0.5(с1h)2 fxx″(x,y+c1hf)+o(h3) } =
=c2f(x,y)+c3{f(x,y)+c1hffy′(x,y)+0.5(с1hf)2 fyy″(x,y)+o(h3)+
+c1h[fx′(x,y)+c1hffxy″(x,y)+o(h2)]+0.5 (с1h)2[fxx″(x,y)+o(h)]}=
=(c2+c3)f+c1c3h(ffy′+fx′)+0.5c12c3h2(f2fyy″ + 2ffxy″+fxx″)+o(h3).
20
21.
МЕТОДЫ РУНГЕ-КУТТА2. Разложим точное решение дифференциального
уравнения y(x+h) в точке х в ряд Тейлора и преобразуем.
1
h
h2
y x O h3
y x h – y x y x y x
h
2
6
h df h 2 d 2 f
3
f
O
h
.
2
2 dx 6 dx
df (x, y) d 2 f (x, y )
,
Найдем полные производные:
dx
dx 2
df ( x, y) f dx f dy
f x' f y ' f
dx
x dx y dx
21
22.
МЕТОДЫ РУНГЕ-КУТТАd 2 f (x, y )
dx
2
d
d
d
f x' f y'f f x'
f y'f
dx
dx
dx
¶ 2 f dy
df
d
ўў +
= f xx
+ f y' + f
f y' ) =
(
¶ x ¶ y dx
dx
dx
2
ў
ў
ў
ў
ўў + f yy
ўў f ) =
= f xx + f xy f + f y' f x' + f (f y' ) + f (f xy
2
2
ў
ў
ў
ў
ў
ў
= f xx + 2 ff xy + f f yy + f x' f y' + f ( f y' )
22
23.
МЕТОДЫ РУНГЕ-КУТТАТаким образом,
R x, y –
y(x h) y(x)
1
c2 c3 – 1 f c1c3 – h ff y f x
h
2
=0
2
ц
2ц
ж
h2 ж
1
h
2
2
3
ч
ч
з
з
ў
ў
ў
ў
ў
ў
+
c
c
–
f
f
+
2
ff
+
f
f
ў
f
ў
+
f
f
ў
–
O
h
.
ч
(
)
ч
зз 1 3
yy
xy
xx
з
x y
y
ч
ч
и
ш
2 и
3ш
6
(
Если потребовать
)
( )
1
c2 c3 – 1 0; c1c3 – 0 , то
2
как бы мы ни выбирали константы, последний член не
сможет обратиться в нуль, так что самое большое, что
мы можем иметь, это R=o(h2).
23
24.
МЕТОДЫ РУНГЕ-КУТТАДля упрощения переобозначим c3 = , c1 = .
1
Тогда c2 = 1 – , .
2
В итоге получим двухпараметрическое семейство
разностных схем второго порядка аппроксимации
вида:
yk+1 = yk +(1– )hf(xk,yk)+ hf(xk+ h,yk + hf(xk,yk)).
Рассмотрим частные случаи.
24























 mathematics
mathematics








