Similar presentations:
Методы построения математических моделей на основе активного эксперимента
1.
Методы построенияматематических моделей на основе
активного эксперимента
2. Оптимальное планирование эксперимента при изучении свойств многокомпонентных систем (МКС)
1. Особенности планирования эксперимента приизучении свойств смесей.
2. Вид уравнений для описания свойств МКС.
Приведенные полиномы Шеффе.
3. Симплекс – решетчатые планы Шеффе.
4. Вычисление коэффициентов приведенных
полиномов Шеффе.
5. Проверка адекватности уравнения регрессии.
6. Планирование эксперимента при исследовании МКС
на локальных участках диаграмм.
3. 1. Особенности планирования эксперимента при изучении свойств смесей
При изучении свойств смеси, зависящих только от соотношенийкомпонентов, факторное пространство в силу соотношения:
q
xi 1,
i 1
(1)
где xi ≥0 i 1, q – концентрация i-го компонента в смеси;
q – количество компонентов в смеси;
представляет собой правильный (q–1)-мерный симплекс.
Симплекс в k – мерном пространстве это выпуклый многогранник,
имеющий ровно (k+1) вершину, каждая из которых определяется
пересечением k гиперплоскостей данного пространства:
для двухкомпонентных систем симплекс – прямая линия;
для трехкомпонентных систем правильный симплекс –
равносторонний треугольник;
для четырехкомпонентных систем симплекс – тетраэдр.
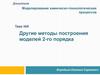
На рис. 1 и 2 представлены разновидности представления
трехкомпонентных систем на двухмерном симплексе.
4.
Рис 1. Концентрационныйтреугольник Гиббса
Рис 2. Концентрационный
треугольник Розебума
5. 2 . Вид уравнений для описания свойств МКС. Приведенные полиномы Шеффе
• Поверхности отклика в МКС имеют сложный характер, поэтому дляадекватного описания таких поверхностей требуются полиномы высоких
степеней и, как следствие, большое количество опытов.
• Обычный полином степени n от q переменных имеет Cqn n
коэффициентов
yˆ b0
bi xi bij xi x j bijk xi x j xk
1 i q
1 i j q
1 i j k q
bi i
xi xi
i
n
1 2, ,
1 2
xin , (2)
где xi (i 1, q ) – концентрации компонентов смеси.
• Шеффе ввел каноническую форму полинома (приведенные полиномы),
число коэффициентов которого значительно меньше, чем обычного.
Рассмотрим, в качестве примера, получение приведенного полинома
второй степени для тройной системы.
Обычный полином (содержит 10 коэффициентов):
yˆ b0 b1 x1 b2 x2 b3 x3 b12 x1 x2 b13 x1 x3 b23 x2 x3
b11 x12 b22 x22 b33 x32 .
(3)
6.
Так какx1 x2 x3 1,
то
b0 x1 b0 x2 b0 x3 b0
x12 x1 x1 x2 x1 x3 ;
x22 x2 x1 x2 x2 x3 ;
x x3 x1 x3 x2 x3 .
2
3
2
2
2
b
,
x
,
x
,
x
После подстановки
0
1
2
3
в (3) получим :
yˆ (b 0 b1 b11 ) x1 (b 0 b 2 b 22 ) x2 (b 0 b 3 b 33 ) x3
(b12 b11 b 22 ) x1 x2 (b13 b11 b 33 ) x1 x3 (b 23 b 22 b 33 ) x 2 x3 .
Обозначим:
i b0 bi bii , ij bij bii b jj .
Тогда приведенный полином 2-й степени от 3-х переменных:
yˆ 1 x1 2 x3 3 x3 12 x1 x2 13 x1 x3 23 x2 x3 .
Т.о., число коэффициентов уменьшилось с 10-ти до шести.
В общем случае приведенный полином 2-ой степени от q
переменных записывается:
yˆ
1 i q
i xi
1 i j q
ij xi x j .
7. 3. Симплекс – решетчатые планы (СРП) Шеффе
В настоящее время наибольшее применение для исследованиясвойств МКС получили СРП, предложенные Шеффе. Эти планы
обеспечивают равномерный разброс экспериментальных точек
по (q -1) – мерному симплексу.
Симплекс – решетчатые планы являются насыщенными планами,
то есть число опытов в этих планах равно числу неизвестных
коэффициентов полинома.
Алгоритм построения плана заключается в следующем:
а) определяется шаг изменения концентрации компонентов 1/n,
где n – степень полинома;
б) по каждому компоненту задается (n+1) одинаково расположенных
уровней:
xi 0, 1 n , 2 n ,
, n n 1;
(4)
в) выбираются все возможные комбинации с такими значениями
концентраций компонентов, которые удовлетворяют
нормирующему соотношению (1).
8.
Графическая интерпретация некоторых{3,n} – решеток
Для полинома
2-го порядка
Для полинома неполного
3-го порядка
Для полинома
3-го порядка
{3,2}
{3,3*}
{3,3}
x23
x3
x2
x13
Рис. 1
x223
• x12
x2
x23
•x
• x12
x123
1
x3
•x
13
Рис. 2
x23
3
•x1 x3
• x122
x
x133
x2
• x112
123
x113
Рис. 3
•x
1
9.
Симплекс-решетчатые планы являютсячастично композиционными:
неполную кубическую решетку {3,3*}
можно получить из {3,2}-решетки, добавив
только одну точку в центре симплекса
(см. рис 2.);
решетку {3,4} получают добавлением
соответствующих точек к решетке {3,2}.
10.
Примеры построения матриц планированиядля решеток {3,2} и {3,3}
1) Матрица планирования для {3,2}-решетки.
(см. рис. 1)
Таблица 1
№
опыта
X1
X2
X3
yiэ
1
1
0
0
y1
2
0
1
0
y2
3
0
0
1
y3
4
1/2
1/2
0
y12
5
1/2
0
1/2
y13
6
0
1/2
1/2
y23
Число опытов:
C
n
q n 1
C 6
2
4
11.
2) Матрица планирования для {3,3}-решетки.(см. рис. 3)
Таблица 2
№
X1
X2
X3
yiэ
1
1
0
0
2
0
1
0
3
0
0
1
4
2/3
1/3
0
5
1/3
2/3
0
6
0
2/3
1/3
7
0
1/3
2/3
8
1/3
0
2/3
9
2/3
0
1/3
10
1/3
1/3
1/3
y1
y2
y3
y112
y122
y223
y233
y133
y113
y123
опыта
Число опытов:
C
n
q n 1
C 10
3
5
12.
4. Вычисление коэффициентов приведенныхполиномов Шеффе
Вывод формул вычисления коэффициентов приведенного
полинома второй степени для трехкомпонентной смеси
yˆ 1 X 1 2 X 2 3 X 3 12 X 1 X 2 13 X 1 X 3 23 X 2 X 3 .
При подстановке координат 1-ой точки
получим:
y1 1 .
и третьей точки:
(X1=1, X2=0, X3=0)
Соответственно после подстановки второй
2 y2 , 3 y3 .
(X1=1/2, X2=1/2,
При подстановке координат 4-ой точки
получим:
y12 1 1 2 2 1 2 12 1 4 .
X3=0)
13.
Так какi yi
, то имеем
y12 y1 1 2 y2 1 2 12 1 4 .
Из последнего уравнения находим
12 4 y12 2 y1 2 y2 .
Соответственно можно найти:
13 4 y13 2 y1 2 y3 ;
23 4 y23 2 y2 2 y3 .
14.
Коэффициентыприведенного
полинома
Шеффе
второго
порядка в общем случае для q - компонентной смеси
yˆ
x
1 i q
i
i
1 i j q
ij xi x j
определяются аналогично:
i yi , ij 4 yij 2 yi 2 y j .
(5)
Аналогичным образом можно вывести формулы для
определения коэффициентов полиномов более высокого
порядка (3-го, непол-ного 3-го и 4-го)
для в общем случае q - компонентной смеси.
Формулы приведены в учебнике
С.Л. Ахназарова, В.В. Кафаров. «Методы оптимизации эксперимента
в химической технологии».
15.
5. Проверка адекватности УРПосле вычисления коэффициентов уравнения регрессии
необходимо провести статистический анализ результатов:
а) проверить адекватность УР;
б) построить доверительные интервалы для значений
функции отклика yˆ , предсказываемые по УР.
Так как при постановке эксперимента по симплекс –
решетчатым планам нет степеней свободы для проверки
адекватности УР (планы насыщенные), то для проверки
адекватности ставят опыты в дополнительных,
так называемых контрольных точках (КТ).
Число КТ и их координаты связаны с постановкой задачи и
особенностями эксперимента. При этом стараются предусмотреть возможность использования КТ для улучшения модели в
случае ее неадекватности.
16.
Остаточная дисперсия (дисперсия адекватности ) в этомслучае определяется по контрольным точкам (КТ)
S
2
ост
1
f ост
l
k
k 2
ˆ
(
y
y
i i),
(6)
i 1
где; l – число контрольных точек; fост= l – 1 – число степеней
k
свободы остаточной дисперсии; yi – средние экспериментальные
k
значения выходной переменной в КТ; yˆ i – значения, рассчитанные
в соответствующих КТ по УР.
При этом, если l >2, то адекватность можно проверить по
критерию Фишера, а ошибку эксперимента S02 (при числе
параллельных опытов в каждой точке симплекса равном m)
рассчитать по формуле:
l
l
1
2
1
S02
S
i
N
l
N
l
i 1
i 1
l m
1 m
2
2
1
y
y
(
y
y
)
iu
i
iu
i
N
l
(
m
1
)
m
1
u 1
i 1 u 1
при условии однородности усредняемых дисперсий, полученных по
параллельным опытам во всех точках симплекса, проверяемой по
критерию Кохрена.
17.
Если адекватность УР оценивается в каждой контрольнойточке, то можно воспользоваться следующим соотношением
(для оценки используется критерий Стьюдента):
t
y m
t q ( f 0 ),
S0 1
l
(7)
где y y yˆ – разность между средним экспериментальным и
расчетным по УР значением выходного параметра; m – число
параллельных опытов в каждой точке; S0 – с.к.о. опытных
данных; ε – величина, связанная с коэффициентами уравнения
(берется из диаграмм, либо таблиц); q – уровень значимости;
l – число контрольных точек; f0 – число степеней свободы
дисперсии воспроизводимости S02.
Если неравенство выполняется для всех КТ, то УР признается
адекватным, иначе УР неадекватно и нужно повышать его
порядок.
При
этом,
если
правило
композиционности
выполняется, то в план включают КТ и переходят к расчету
коэффициентов УР более высокого порядка.
18.
ПОСТРОЕНИЕ СИМПЛЕКС-РЕШЁТЧАТЫХПЛАНОВ И ПОЛИНОМОВ ШЕФФЕ
Лабораторная работа №4
“Оптимальное планирование эксперимента при
изучении свойств многокомпонентных систем”
19.
1. Физический смысл задачиПри создании композиционных, в частности полимерных (в том числе
энергонасыщенных) материалов (ПКМ), с заданными свойствами в их состав
вводят твердые дисперсные наполнители (ТДН), влияющие как на физикомеханические, так и на другие свойства материала.
Довольно часто в качестве ТДН используют зерненые наполнители, которые
характеризуются средне-массовым размером частиц и пористостью. Под пористостью понимается величина объема не занятого частицами наполнителя после
заполнения ими единичного объема, например равного 1дм3.
В некоторых случаях, с целью улучшения физико-механических и других
свойств материала, возникает необходимость увеличения доли единичного
объема занятого наполнителями. Для этого в состав материала вводят в
соответствующих объемных долях фракции наполнителя с разными среднемассовыми размерами частиц и пористостями. В результате плотность упаковки
смеси ТДН (доля объема занятого в единичном объеме фракциями наполнителя
– параметр φm ) возрастает. Плотность упаковки φm зависит от размеров частиц
di , пористостей pi выбранных фракций, их долей vi в составе наполнителя и
может быть рассчитана через указанные параметры известными методами.
В лабораторной работе необходимо для заданных числа фракций ТДН и
степени полинома Шеффе: построить симплекс-решетчатый план относительно
объемных долей фракций; рассчитать в точках плана по соответствующей
программе значения φm; по результатам вычислительного эксперимента
определить коэффициенты полинома и оценить его адекватность путем расчета
по нему φm в контрольных точках (КТ). В формализованном виде смысл и
геометрическая интерпретация задачи представлены на следующем слайде.
20.
2. Математический смысл и геометрическаяинтерпретация задачи
Дано: {q,n}-решетка; q – число фракций ТДН в составе
композиционного материала, n – степень полинома.
Параметры фракций ТДН :
di
d1
d2
...
dq
pi
p1
p2
…
pq
p p ,p ,
1
2
– размеры частиц фракций;
p i 1, q – пористости фракций.
d i i 1, q
i
где
где
m
p
p
d d1 , d 2 , , dq
q
V=1 дм3
d1
d2
m p 1,
– плотность упаковки смеси ТДН;
– пористость смеси фракций ТДН.
v v1 , v2 ,
m f d , p, v ,
, vq
p m
– объемные доли фракций ТДН.
21.
3. Задание на выполнение лабораторной работы3.1. Составить СРП для заданной {q,n}-решетки относительно объемных
долей фракций ТДН для полного симплекса: 0 vi 1, i 1, q .
Матрица планирования формируется по алгоритму, приведенному в лекции.
Пример. СРП для {3,3}-решетки.
№
опыта
1
2
3
4
5
6
7
8
9
10
v1
v2
v3
1
0
0
2/3
1/3
0
0
1/3
2/3
1/3
0
1
0
1/3
2/3
2/3
1/3
0
0
1/3
0
0
1
0
0
1/3
2/3
2/3
1/3
1/3
φm
φ1
φ2
φ3
φ112
φ122
φ223
φ233
φ133
φ113
φ123
3.2. Для каждого опыта матрицы
планирования СРП рассчитать
плотность упаковки φm. Расчет
m f d , p, v осуществлять
по
программе “UPAK”.
3.3. Построить полином Шеффе,
определив его коэффициенты, и
оценить адекватность полинома
по 2-м контрольным точкам (КТ).
22.
6. Планирование эксперимента при исследовании МКСна локальных участках диаграмм
При изучении свойств q-компонентных смесей часто возникает
необходимость исследования зависимости свойства от состава не во всей
области изменения концентрации компонентов
0 xi 1 , а в локальном
участке диаграммы:
(8)
0 ai xi bi 1,
i 1, q .
В этом случае возможны два варианта:
1) Исследуемая область – симплекс
Изучаемая локальная область на диаграмме может представлять собой
неправильный, либо правильный симплекс, координаты вершин которого
известны:
A1 x1(1) , x2(1) , , xq(1) , A2 x1(2) , x2(2) , , xq(2) ,
, Aq x1( q ) , x2( q ) ,
xq( q ) .
Чтобы иметь возможность применять в этом случае планы, используемые
для полных диаграмм, проводят перенормировку и принимают составы в
вершинах Aj j 1, q за самостоятельные псевдокомпоненты
так, чтобы
q
для всей области локального симплекса выполнялось условие zi 1.
i 1
Планирование экспериментов осуществляется в системе координат
псевдокомпонентов. Относительно новых переменных z1, z2, …, zq, могут
быть построены все ранее рассмотренные планы.
23.
Для проведения экспериментов необходимо перейти от псевдокомпонентов zi к исходным компонентам xi . Для любой u-й точки планаэтот перерасчет осуществляется по формуле
xi(u ) xi(1) z2(u ) ( xi(2) xi(1) ) z3(u) ( xi(3) xi(1) ) zq(u) ( xi( q) xi(1) ),
где xi – содержание i-ого компонента в вершине zj (Aj).
После реализации плана рассчитывают коэффициенты УР в координатах
псевдокомпонентов
(9)
yˆ f z1 , z2 , , zq ,
используя ранее приведенные формулы для соответствующих планов, и
проверяют его адекватность. Для практического использования уравнение
(9) записывается в исходной системе координат при помощи формул
перевода координат из одной афинной системы в другую:
z1 z1(1) x2 ( z1(2) z1(1) ) x3 ( z1(3) z1(1) )
xq ( z1( q ) z1(1) ),
z2 z2(1) x2 ( z2(2) z2(1) ) x3 ( z2(3) z2(1) )
xq ( z2( q ) z2(1) ),
...........................................................................................
zq 1 zq(1) 1 x2 ( zq(2) 1 zq(1) 1 ) x3 ( zq(3) 1 zq(1) 1 )
zq 1 z1 z2
zq 1.
xq ( zq( q )1 zq(1) 1 ),
24.
Значенияzi( j )
находятся из решения (q-1)-й систем уравнений:
x1(1) z1(1) x2(1) z1(2) x3(1) z1(3)
xq(1) z1( q ) 1
(2) (1)
xq(2) z1( q ) 0
x1 z1 x2(2) z1(2) x3(2) z1(3)
................................................................
x ( q ) z (1) x ( q ) z (2) x ( q ) z (3)
( q) (q)
x
z1 0
q
1
1
2
1
3
1
x1(1) z1(1) x2(1) z1(2) x3(1) z1(3)
xq(1) z1( q ) 0
(2) (1)
xq(2) z1( q ) 1
x1 z1 x2(2) z1(2) x3(2) z1(3)
.................................................................
x ( q ) z (1) x ( q ) z (2) x ( q ) z (3)
(q) (q)
x
0
q z1
2
1
3
1
1 1
..................................................................
x1(1) z1(1) x2(1) z1(2) x3(1) z1(3)
xq(1) z1( q ) 0
(2) (1)
xq(2) z1( q ) 0
x1 z1 x2(2) z1(2) x3(2) z1(3)
..................................................................
x ( q ) z (1) x ( q ) z (2) x ( q ) z (3)
( q) ( q)
x
1
q z1
2
1
3
1
1 1
25.
2) Исследуемая область – многогранникПри наличии ограничений на изменение концентраций
компонентов исследуемая область в общем случае образует
некоторый выпуклый многогранник, который
образуется в
результате
пересечения
ограничений с
нормирующим
q
соотношением xi 1. В данном случае для построения плана
экспериментов i 1 необходимо некоторым образом распределить
экспериментальные точки по получающемуся из условия
0 ai xi bi 1,
i 1, q
многограннику, исключив при этом следующие вырожденные
случаи:
q
a
i 1
i
1
q
и
b
i 1
i
1.
26.
ОЦЕНКА АДЕКВАТНОСТИ ПОЛИНОМОВ ШЕФФЕ1. Дано: S02 – дисперсия воспроизводимости опытов;
m – число параллельных опытов.
2. Дисперсия предсказанного значения S 2yˆ определяется
по закону накопления ошибок:
S 2yˆ
S02
,
m
где
f x1 , x2 ,
, xq
(1)
.
Например, для {q, n=2}-решётки имеем:
где
1 i q
ai2
1 i j q
aij2 ,
ai xi 2 xi 1 , aij 4 xi x j .
(2)
27.
3. Проверку адекватности проводят в каждой контрольнойточке (КТ). Для этого:
1) Составляют отношение:
tр
y
y m
,
S 2y S y2ˆ S0 1
(3)
где S 2y S02 m
– дисперсия средних значений;
y y э yˆ – модуль разности между средним
экспериментальным значением в КТ и расчетным
значением.
2) Величина t р распределена по закону Стьюдента.
Поэтому, если t р tТ q l , f , то полином адекватен, (4)
где tT – табличное значение критерия Стьюдента;
q – уровень значимости;
l – число контрольных точек;
f – число степеней свободы.


























 mathematics
mathematics physics
physics