Математическое описание волнового движения

1.

Волны
Лекция 4-01
Математическое описание
волнового движения
9 февраля 2022 года
Лектор: доцент НИЯУ МИФИ,
Ольчак Андрей Станиславович

2.

Уравнения Максвелла
ВСПОМНИМ, чем завершался курс лекций 3-го семестра:
Дж.К. Максвелл в 1859 г. сформулировал систему уравнений, исчерпывающим
образом описывающих единое электро-магнитное поле.
Уравнения Максвелла в локальной и интегральной форме
B
E
t
D
D
H jпров
t
B 0
d
E d l B dS
dt S
B dS 0
стор
D dS стор dV
V
d
H d l jпров dS D dS
dt S
S
J.C. Maxwell

3.

Уравнения Максвелла
Свойства уравнений Максвелла
1. Уравнения выполняются во всех инерциальных системах отсчёта.
(являются релятивистски инвариантными).
2. Уравнения линейные, благодаря чему выполняется принцип
суперпозиции для магнитных и электрических полей.
3. Уравнения не симмметричны относительно E и B => эти поля
проявляют себя по разному.
4. Уравнения содержат все известные законы электродинамики:
Кулона, Био-Савара-Лапласа, уравнение непрерывности и т.п.
5. Из
уравнений Максвелла следует возможность
существования и распространения
электромагнитных волн в вакууме.

4.

Ур-ния Максвелла и скорость света
В изотропной среде без зарядов и токов Н = B/μ0μ ; D = ε0 εE
div D = div Е = 0 rot E = -дB/дt
div B = 0
rot Н = +дD/дt =
>
=> rot B/μ0μ = ε0 εдE/дt
=> rot B = μ0με0 ε дE/дt = (1/c2)дE/дt
с = (μ0με0 ε)-1/2 [м/с] – скорость света в среде μ, ε
с0 = (μ0ε0)-1/2 = 3*108м/с - скорость света в пустоте μ=ε=1
= максимально возможная скорость распространения чего бы то ни
было во Вселенной
с = (μ0με0 ε)-1/2 = с0 (με)-1/2 =~ с0/ε 1/2 = с0 /n =>
Оптическая плотность среды (показатель преломления) n =~ ε1/2
Удивительные результаты, обнаружившие ранее не замеченную
связь оптики и электромагнетизма

5.

Уравнения Максвелла
Уравнения Максвелла в изотропной среде без зарядов и токов
div Е = 0
дB/дt = - rot E
div B = 0
дE/дt = +с2rot B = >
«Поиграем» с дифференциальными операторами
д2В/дt2 = - д(rot Е)/дt = - с2rot rot B =
= - с2(grad div B - ∆B) = с2∆B
д2E/дt2 = с2д(rot B)/дt = - с2rot rot E = с2∆E
Система уравнений Максвелла в изотропной среде без зарядов и
токов сводится всего к ДВУМ математически одинаковым
уравнениям, определяющим поведение электрической Е и
магнитной В компонент поля, и имеющим волновые решения.

6.

Решения 1-мерных уравнений Максвелла
1-мерные ур-ния Максвелла в изотропной среде без зарядов и токов
д2E/дt2 = с2∆E = с2д2E/дх2 ; д2B/дt2 = с2д2В/дх2
Решение: т.н. бегущая волна
E = Е0 f(y) , В = В0 f(y); y = x+tс
f – любая (!) математическая функция одной переменной y = x+tс.
ДОКАЖЕМ. дE/дt = (дE/дy)(дy/дt) = +c дE/дy;
д2E/дt2 = +c(д2E/дy2(дy/дt) = c2 д2E/дy2
с2∆E = с2д2E/дx2 = с2д2E/дy2
Ч.Т.Д. !
Конкретный вид функции f определяется т.н. начальными
условиями задачи – то есть, видом функции распределения полей
Е(х), В(х) в начальный момент времени t = 0

7.

Волновые решения уравнений Максвелла
Решение ур-ний Максвелла в изотропной среде без зарядов и токов
д2E/дt2 = с2д2E/дх2 ; д2B/дt2 = с2д2В/дх2
Решение (в одномерном случае): т.н. бегущая волна
E = Е0 f(x+сt)) , В = В0 f(x+ct))
Конкретный вид функции f определяется начальными условиями
задачи – т.е. видом функций Е(х), В(х) в момент времени t = 0
ПРИМЕР.
E(x, t=0) = Е0 cos(2πx/λ)) = Е0 cos(ωx/c) =>
E(x, t) = Е0 cos(ω(x + ct)/c) = Е0 cos(2πx/λ + ωt) =>
=> E(x, t) = Е0 cos(2π(x/λ + t/T)
Если начальная конфигурация поля = гармоническая функция,
такой она останется и далее, но как-бы «побежит» по оси ОХ
(если аргумент (х - сt) или против оси ОХ (если (х+ct). Чтобы
определить, куда бежит волна, надо знать второе начальное
условие: вид производной функции дE(x, t)/ дt при t = 0

8.

Волновые решения уравнений Максвелла
Решение одномерных ур-ний Максвелла в изотропной среде без
зарядов и токов – бегущая волна
E = Е0 f(x+сt)) , В = В0 f(x+ct))
Конкретный вид функции f определяется начальными условиями
задачи – т.е. видом функций Е(х), В(х) в момент времени t = 0
и видом производных этих функций при t = 0.
Это – электромагнитные волны – очень важное физическое
явление, которое необходимо всесторонне изучать.
Нужность изучения математического описания
волнового движения усугубляется тем, что волны бывают не
только электромагнитные (радио, свет, и др.), но и упругие (звук),
капилярно-гравитационные (на поверхности жидкости) и т.д., и т.п.
Волна – особая, очень распространенная форма движения материи

9.

Волновое движение. Общие свойства
Волны бывают разные:
• По природе: электромагнитные (радио, свет, и др.), упругие
(звук), капиллярно-гравитационные (на поверхности жидкости)
и т.д., и т.п.
• По пространственным характеристикам: одномерные (плоские),
сферические, цилиндрические, …
• По форме: одиночные, цуговые, периодические, гармонические
• … а также бывают волны бегущие и стоячие, продольные и
поперечные, сходящиеся и расходящиеся, нелинейные, ударные,
…. и со всеми надо постепенно разобраться….

10.

Волновое движение. Общие свойства
Волна - процесс распространения колебаний в пространстве,
Причем НЕ ОБЯЗАТЕЛЬНО длительных колебаний, но и коротких
отклонений от средних значений некоторых физических величин в
пространстве.
v
x
t1

11.

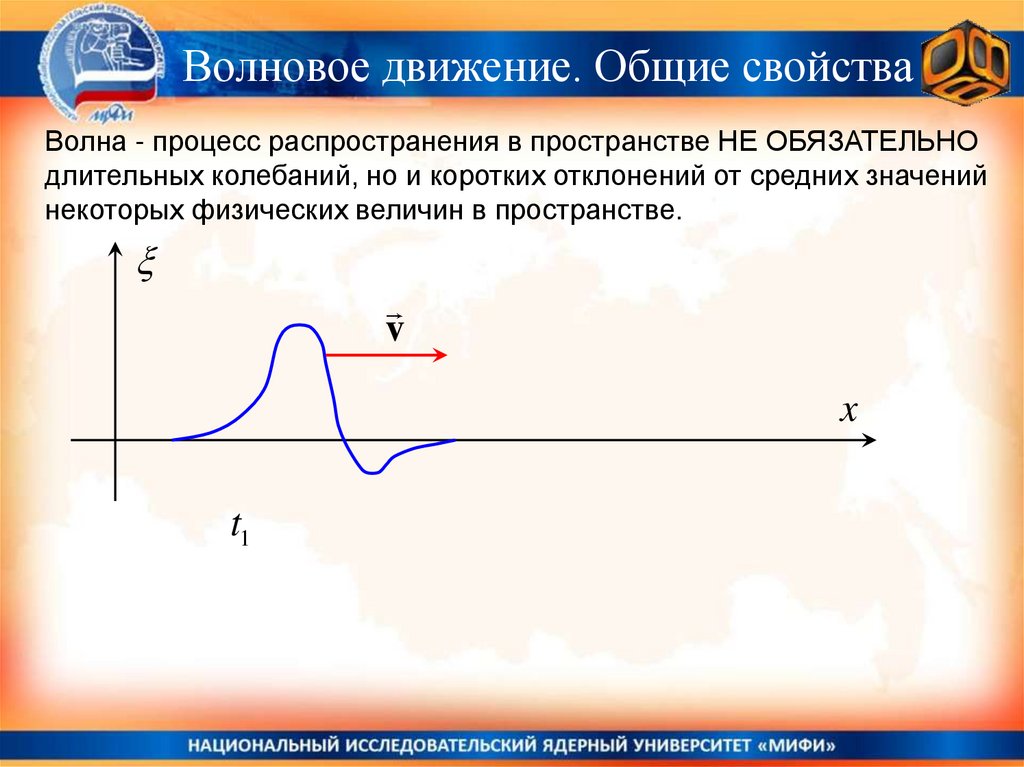
Волновое движение. Общие свойства
Волна - процесс распространения в пространстве НЕ ОБЯЗАТЕЛЬНО
длительных колебаний, но и коротких отклонений от средних значений
некоторых физических величин в пространстве.
v
x
t1

12.

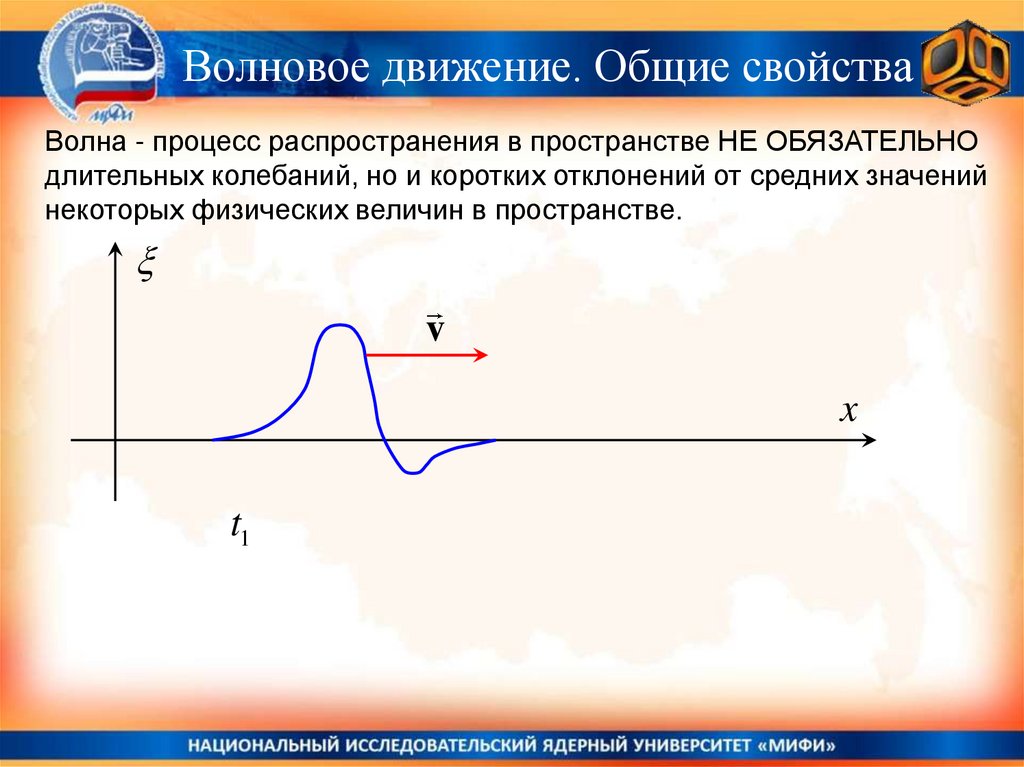
Волновое движение. Общие свойства
Волна - процесс распространения в пространстве НЕ ОБЯЗАТЕЛЬНО
длительных колебаний, но и коротких отклонений от средних значений
некоторых физических величин в пространстве.
v
x
t1

13.

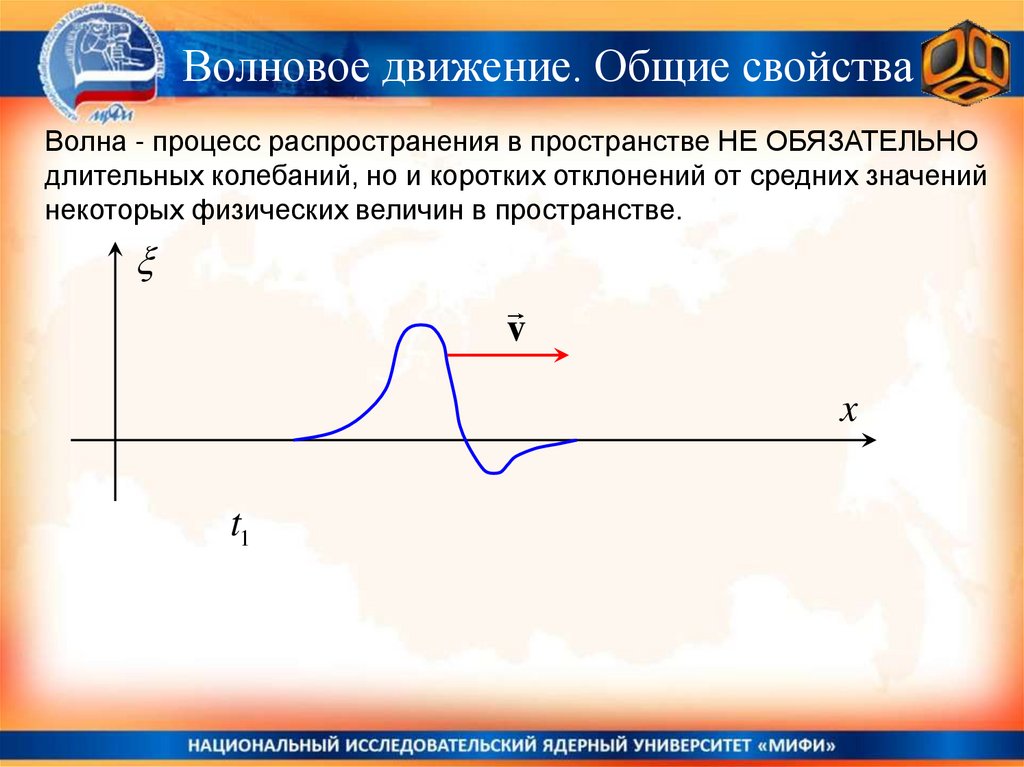
Волновое движение. Общие свойства
Волна - процесс распространения в пространстве НЕ ОБЯЗАТЕЛЬНО
длительных колебаний, но и коротких отклонений от средних значений
некоторых физических величин в пространстве.
v
x
t1

14.

Волновое движение. Общие свойства
Волна - процесс распространения в пространстве НЕ ОБЯЗАТЕЛЬНО
длительных колебаний, но и коротких отклонений от средних значений
некоторых физических величин в пространстве.
v
x
t1

15.

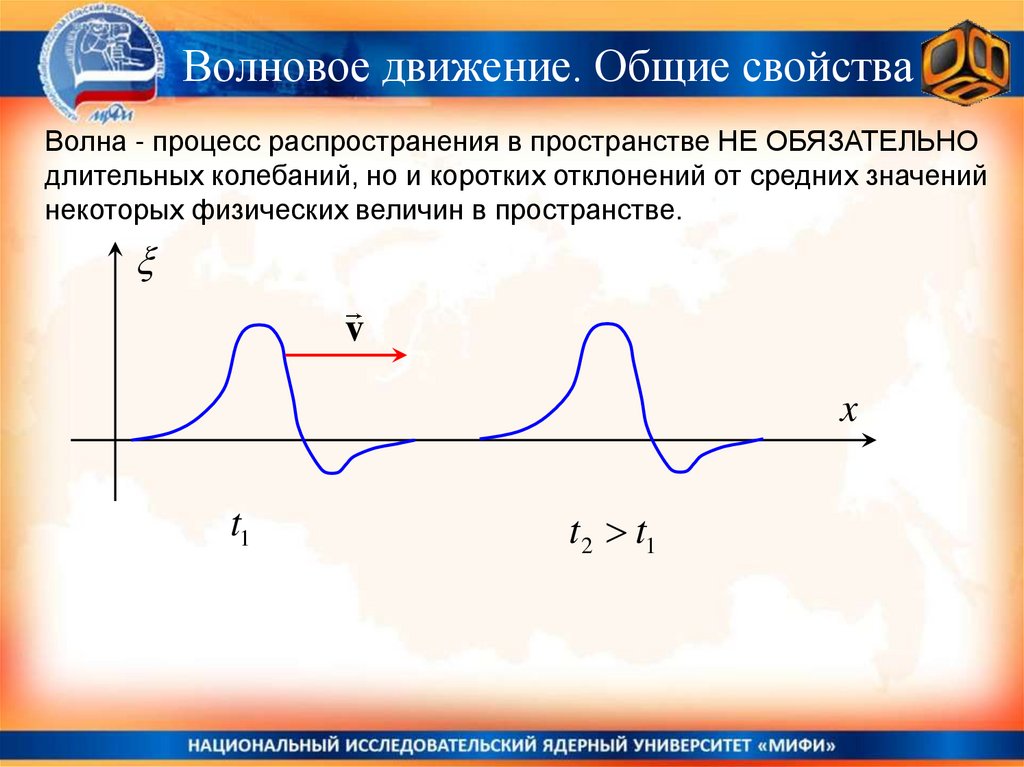
Волновое движение. Общие свойства
Волна - процесс распространения в пространстве НЕ ОБЯЗАТЕЛЬНО
длительных колебаний, но и коротких отклонений от средних значений
некоторых физических величин в пространстве.
v
x
t1
t2 t1

16.

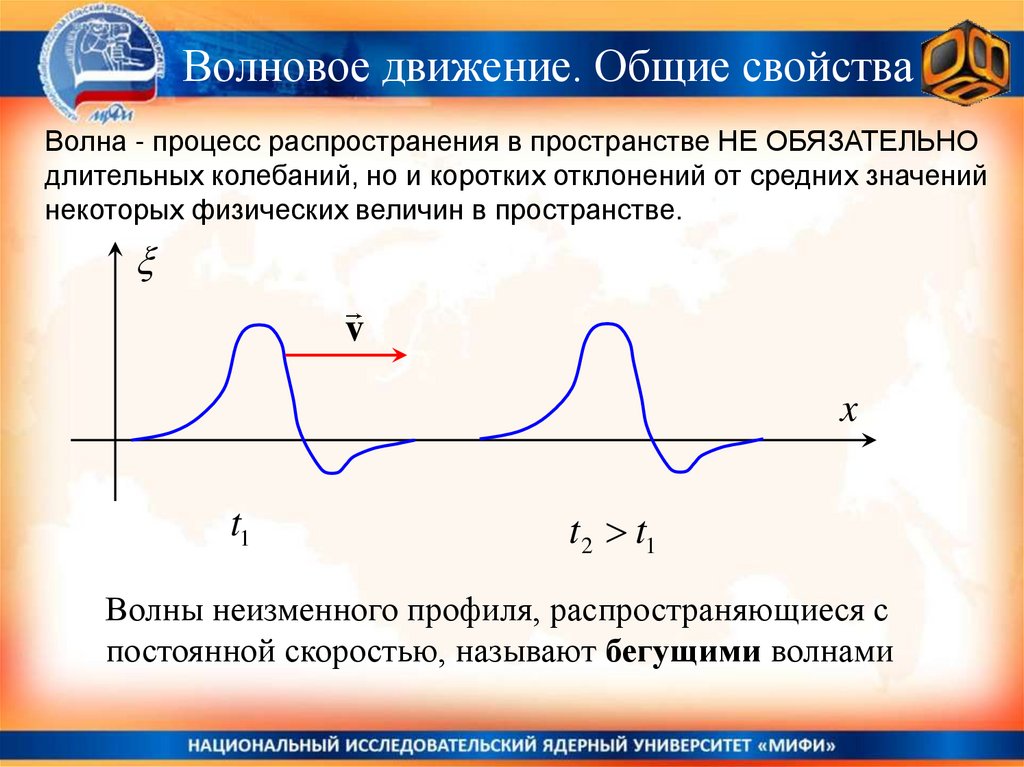
Волновое движение. Общие свойства
Волна - процесс распространения в пространстве НЕ ОБЯЗАТЕЛЬНО
длительных колебаний, но и коротких отклонений от средних значений
некоторых физических величин в пространстве.
v
x
t1
t2 t1
Волны неизменного профиля, распространяющиеся с
постоянной скоростью, называют бегущими волнами

17.

Волновое движение. Общие свойства
Волна - процесс распространения в пространстве НЕ ОБЯЗАТЕЛЬНО
длительных колебаний, но и коротких отклонений от средних значений
некоторых физических величин в пространстве.
x, t f x vt
x, t g x vt
v
x
t1
t2 t1
Волны неизменного профиля, распространяющиеся с
постоянной скоростью, называют бегущими волнами

18.

КЛАССИФИКАЦИЯ ВОЛН ПО ИХ ФОРМЕ
Одиночная волна или импульс
представляет
собой
короткое
возмущение, не имеющее регулярного
характера.
v
x
t1
t2 t1

19.

КЛАССИФИКАЦИЯ ВОЛН ПО ИХ ФОРМЕ
Одиночная волна или импульс
представляет
собой
короткое
возмущение, не имеющее регулярного
характера.
v
x
t1
Цугом волн называется ограниченный
ряд повторяющихся возмущений.
t2 t1

20.

КЛАССИФИКАЦИЯ ВОЛН ПО ИХ ФОРМЕ
Одиночная волна или импульс
представляет
собой
короткое
возмущение, не имеющее регулярного
характера.
v
x
t1
Цугом волн называется ограниченный
ряд повторяющихся возмущений.
Если длительность цуга значительно
превышает период колебаний τ/T >> 1,
то такой цуг волн называется
периодической
квазимонохроматической волной.
t2 t1

21.

КЛАССИФИКАЦИЯ ВОЛН ПО ИХ ФОРМЕ
Одиночная волна или импульс
представляет
собой
короткое
возмущение, не имеющее регулярного
характера.
v
x
t1
Цугом волн называется ограниченный
ряд повторяющихся возмущений.
Если длительность цуга значительно
превышает период колебаний τ/T >> 1,
то такой цуг волн называется
квазимонохроматической волной.
Когда τ/T → ∞ волна становится
гармонической монохроматической.
(если колебания
происходят
по
гармоническому закону)
t2 t1

22.

КЛАССИФИКАЦИЯ ВОЛН ПО ИХ ФОРМЕ
Одиночная волна или импульс
представляет
собой
короткое
возмущение, не имеющее регулярного
характера.
v
x
t1
Цугом волн называется ограниченный
ряд повторяющихся возмущений.
x, t f x vt
Если длительность цуга значительно
превышает период колебаний τ/T >> 1,
то такой цуг волн называется
квазимонохроматической волной.
x, t g x vt
Когда τ/T → ∞ волна становится
монохроматической. (если колебания
происходят по гармоническому закону)
t2 t1

23.

Волновые уравнения
Одномерные волновые уравнения
x, t f x vt
x, t g x vt
}
<=> д2ξ /дt2 = v2д2ξ /дх2
дξ /дt = - vдξ /дх => ξ = f(x-vt)
дξ /дt = vдξ /дх => ξ = g(x+vt)
Трехмерное волновое уравнение
2
дξ
2
/дt
=
2
v Δξ

24.

Гармоническая волна
x, t f x vt
x, t g x vt
<=> д2ξ /дt2 = v2д2ξ /дх2
x 0 : 0, t a cos t
x, t a cos t x v
v
x, t a cos t x v
v
x
Фазовая
скорость
волны
- циклическая частота волны
T 2 - период волны 1 T 2 - частота волны
t x v - фаза - начальная фаза
a 0 - амплитуда волны

25.

Гармоническая волна
Длина волны – это наикратчайшее расстояние между
двумя точками среды, фазы которых отличаются на 2 .
v
vT
v
k
2
- волновое число
2
2
k
k
vT
v
x, t a cos t x v = Re[a exp(i(ωt – kx+a))]

26.

Одномерная волна = плоская
x, t a cos t x v
y
n, v
r
z
х
Все точки с одинаковым значением х (и любыми
значениями y, z) образуют плоскость, перпендикулярную
оси 0Х, и все колеблются одинаково (в одной фазе).
Волновая поверхность (в данном случае плоскость) –
геометрическое место точек, колеблющихся в одной фазе
Формально ωx/v = kx = knr = kr,
k = kn = ωn/v – волновой вектор
r , t a cos t k r
2
k
a cos( t knr )
Уравнение волны с волновым вектором k описывает волну в
любой системе координат, причем не только плоскую.

27.

Плоские гармонические волны
Волновая поверхность (плоскость) –
геометрическое место точек, колеблющихся в
одной фазе
a cos( t knr )
r , t a cos t k r
k kn – волновой вектор
k k x ex k y ey k z ez
2
k
a cos t k x x k y y k z z
Re ae
i ( t kr )

28.

Трехмерное волновое уравнение
( r, t ) a cos( t kr )
2
2
2
2
2
v 2 2 2
2
t
y
z
x
2
2
v
2
t
Волновой вектор в любой точке перпендикулярен волновой
поверхности.
Форма волновой поверхности зависит от симметрии задачи.
Для плоских волн это плоскости
Для сферически симметричных волн – концентрические сферы
Для цилиндрически симметричных - соосные цилиндры или (в
двумерном случае) концентрические окружности

29.

Сферические волны
Если r >> λ и d, то источник можно считать точечным, а
волну на этих расстояниях – сферической.
2
2
2
2 1
2
v 2 v 2 r
2
t
t
r r r
f r vt g r vt
r, t
r
a cos t kr
r, t
r
vф
k
a0
a(r)
r

30.

Цилиндрические волны
2 1
v
2
t
2
v
v
,t
v
v
f vt g vt
ξ(ρ,t) = (a0/√ρ)cos(ωt + kρ +α)
vф
k
a(ρ) = (a0 / √ρ)

31.

Курс общей физики НИЯУ МИФИ
Следующая лекция
16 февраля

32.

Примеры решения задач
Вертикальная бесконечная стенка, расположенная в газе,
колеблется вдоль оси, перпендикулярной к стенке. Ёе
смещения описываются законом: = A sin t, где A = 1,0 см,
= 2 рад/с. Для точек среды, находящихся на расстоянии
l = 175 м от стенки, найти смещение от положения равновесия,
скорость и ускорение в момент времени t 0,75 с. Скорость
волны в газе v = 350 м/с. Затуханием волны с расстоянием
можно пренебречь.

33.

Примеры решения задач
x, t A cos t kx
0
0, t A sin t
k
l
x
A cos t
2
k v
x, t Asin t x v

34.

Примеры решения задач
Vx x, t x, t A cos t x v
a x x, t Vx x, t A sin t x v
2
l , t A sin t l v 0,010 м
Vx l , t A cos t l v 0 м/с
a x l , t A 2 sin t l v 0,40 м/с2

35.

Курс общей физики НИЯУ МИФИ
Следующая лекция
16 февраля

36.

Стоячие волны
Наложение двух распространяющихся во встречных направлениях
бегущих плоских волн может образовать стоячую волну:
пад отр a cos t kx a cos t kx
2a cos
t kx t kx
2
cos
t kx t kx
2
2a cos kx cos t 2a sin kx sin t
2
2
Граничные условия:
0, t l , t 0
0, t 0 cos
2
0
2
2

37.

Стоячие волны
2a sin kx sin t
l , t 0 sin kl 0 kl n kn
n 1
n 2
n 3
n 4
k
2
2
n
n
l
n
l
n n
l
, n 1,2,3,...
2
v, n
v
n
nv
n
2l

38.

Стоячие волны
Стоячие волны (эффект сложения двух плоских волн одной длины и
амплитуды, распространяющихся навстречу друг-другу)
A cos(ωt–kx) + A cos(ωt+kx) =
= 2A cos(kx) cos(ωt)
kl/2 = π/2 + πn – условие
существования стоячей волны
На правом конце узел - А(0) = 0
На левом конце пучность - А(l) = 2А
k = 2π/λ

39.

Стоячие волны
Фотография стоячей волны в струне

40.

Стоячие волны
Стоячая волна в колоколе

41.

Стоячие волны
Собственные колебания Земли
При очень сильном землетрясении
отмечены собственные колебания Земли.
От удара сдвинувшихся недр половинки
земного шара закручиваются навстречу
друг другу. Если бы Земля имела твердое
ядро, период колебаний был бы около 32
минут. На самом деле он равен 44 минутам,
что соответствует жидкому ядру.
Относительное смещение частиц при таких
колебаниях не больше 1 мм.

42.

Стоячие волны
Из-за значительной ветровой нагрузки 20 мая 2010 года автомобильный
мост через реку Волгу вошёл в резонанс с амплитудой колебаний в
вертикальной плоскости около 50-60 см

43.

Общая физика, 4-ый семестр
Спасибо за внимание!
Следующая лекция
16 февраля

44.

Нелинейные волны
Дисперсия волн
Образование устойчивой
структуры солитона за счёт
механизма компенсации:
Нелинейные явления
Солитон
Результат:

45.

Нелинейные волны
Солитон, пересекающий Гибралтарский пролив с запада на восток

46.

Нелинейные волны
Игрушечный кораблик в лабораторной кювете демонстрирует
эффект «мертвой воды»: под его винтом образуется внутренняя
волна, «высасывающая» из него скорость

47.

Упругие волны в газе и жидкости
Снимок, сделанный
спутниками НАСА у
побережья Австралии,
показывает разновидность
гигантских воздушных
атмосферных волн,
называемых гравитационными.
Эти волны образуются вблизи
атмосферного фронта. Для их
фиксации требуются радары.

48.

Упругие волны в газе и жидкости
Ударные волны