Волновое движение. Лекция 8

1.

Лекция 8
ВОЛНОВОЕ
ДВИЖЕНИЕ
Вопросы:
1. Виды механических волн и их основные характеристики.
2. Уравнение плоской незатухающей
бегущей волны. Энергия упругих
волн.
3. Интерференция волн. Стоячие волны.

2.

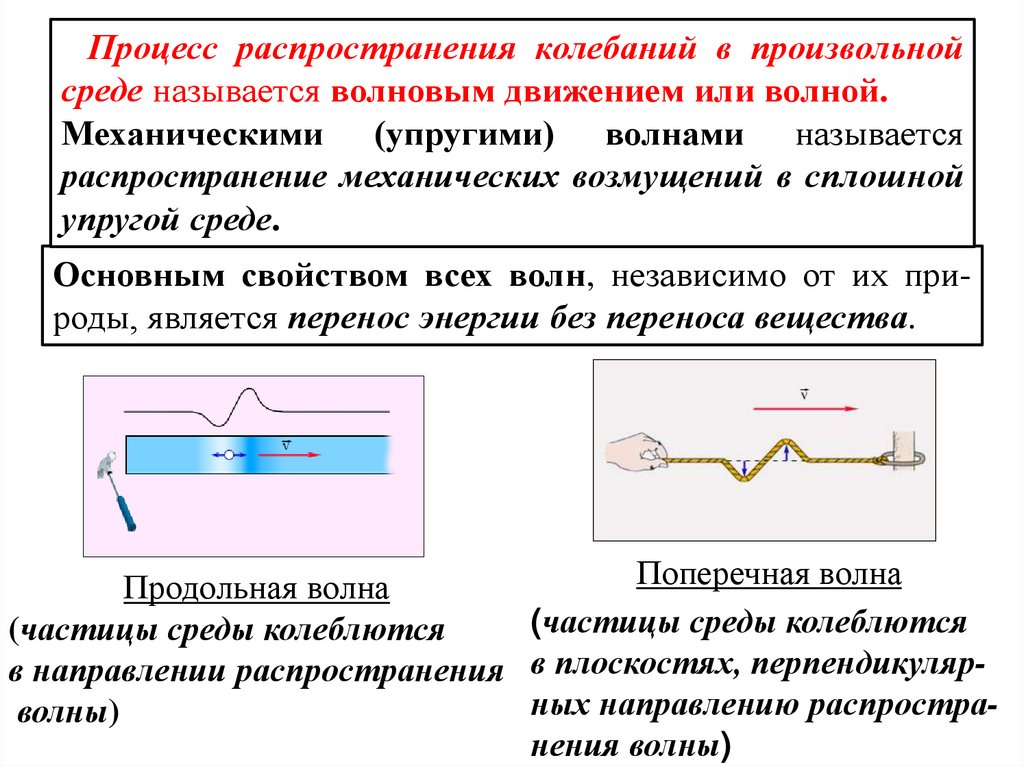
Процесс распространения колебаний в произвольной
среде называется волновым движением или волной.
Механическими (упругими) волнами называется
распространение механических возмущений в сплошной
упругой среде.
Основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.
Поперечная волна
Продольная волна
(частицы среды колеблются
(частицы среды колеблются
в направлении распространения в плоскостях, перпендикулярных направлению распростраволны)
нения волны)

3.

Расстояние между ближайшими частицами среды,
колеблющимися в одинаковой фазе, называется длиной
волны .
Длина волны равна расстоянию, на которое распространяется волна за один период колебаний:
1
υ 2 υ
v =
vT , T
2
– волновое число.
k
v
Геометрическое место точек, до которых колебания
доходят к моменту времени t, называется волновым
фронтом.
Геометрическое место точек, колеблющихся в
одинаковой фазе, называется волновой поверхностью.

4.

Уравнение плоской незатухающей бегущей волны
Уравнением волны называется выражение, которое даёт
смещение колеблющихся частиц среды как функцию её
координат и времени:
= (x, y, z, t).
Бегущими называются волны, которые переносят
в пространстве энергию.
Вид функции в случае плоской волны
(волновые поверхности имеют вид плоскостей):
x
x, t A cos t
v
A cos t x
v

5.

С учетом понятия волнового числа уравнение плоской
незатухающей бегущей волны приобретает следующий
вид:
(x, t) = A cos( t – kx + ),
где ( t
– kx + ) – фаза распространяющейся волны,
– начальная фаза, зависящая от выбора начала отсчета
координаты х и времени t;
A = const. – амплитуда волны.
Если плоская волна распространяется в отрицательном
направлении оси х, то уравнение волны имеет вид:
(x, t) = A cos( t + kx + )

6.

Энергия упругих волн
Средняя объемная плотность энергии, переносимой
волной:
2 2
Дж
W A
w
V
2
m
V
м3
– плотность среды, в которой
распространяется волна.
m – масса частиц среды, находящихся в объеме V.
Количество энергии, переносимое волной через
некоторую поверхность в единицу времени, называется
потоком энергии волны Ф через эту поверхность:
W
Ф
t
[Ф] = Вт.

7.

Для характеристики переноса энергии в
разных точках пространства вводится
векторная величина, называемая плотностью потока энергии j (вектор Умова).
Вт
j wv 2
м
v
S
Умов
Николай
Алексеевич
(1846 – 1915)
W
w S v t
j
wv
S S t
S t
Направление вектора Умова совпадает с направлением
переноса энергии, а его модуль равен энергии, переносимой
волной за единицу времени через единичную площадку,
расположенную перпендикулярно направлению распространения волны.

8.

Интерференция волн
Интерференцией называется наложение в пространстве
двух (или нескольких) когерентных волн, при котором
наблюдается устойчивая во времени картина усиления
колебаний в одних точках и ослабления колебаний – в
других.
M Волны одинаковой частоты ( 1 =
r1
2 = ) называют когерентными,
О1
если колебания, обусловленные
r2
этими волнами в каждой из точек
среды, обладают постоянной разностью фаз.
О2
Э
Схема интерференции
от точечных когерентных
источников O1 и O2

9.

При интерференции колебание в данной точке среды
будет равно сумме колебаний:
1 = A1·cos( t – kr1 + 1),
2 = A2·cos( t – kr2 + 2),
A1 и A2 – амплитуды волн в рассматриваемой точке,
k – волновое число, r1 и r2 – расстояния от источников
где
волн до рассматриваемой точки.
Результат сложения колебаний зависит
от разности хода Δ (разности фаз волн Δφ):
r2 r1
2

10.

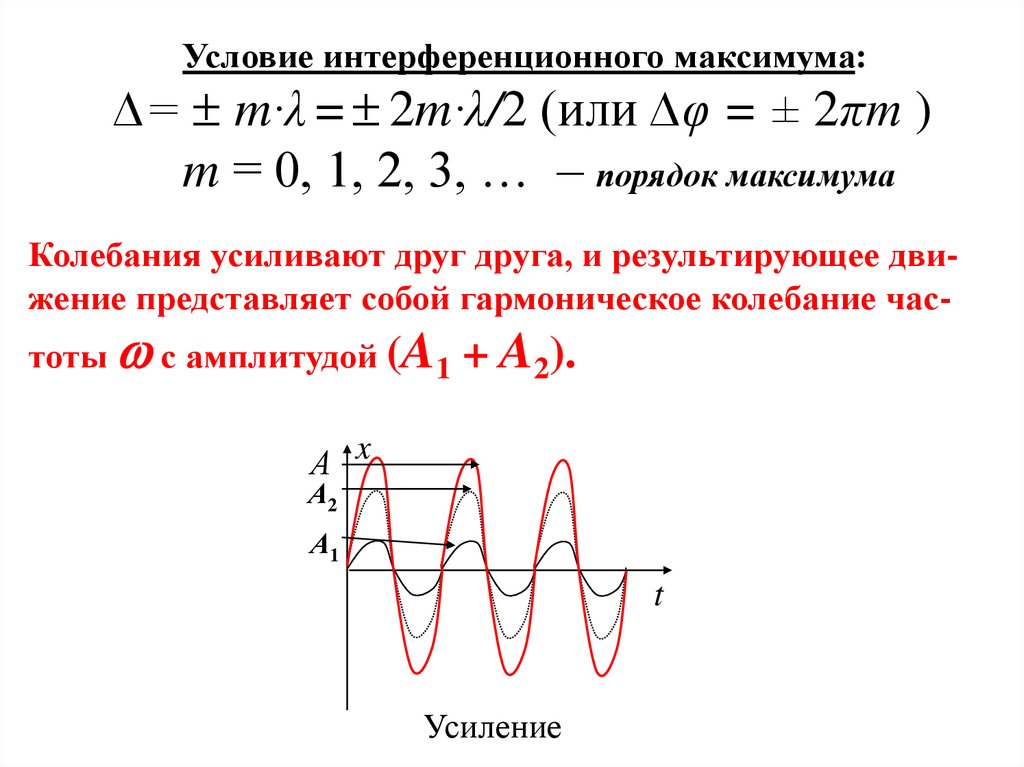
Условие интерференционного максимума:
∆= m·λ = 2m·λ/2 (или ∆φ = ± 2πт )
m = 0, 1, 2, 3, … – порядок максимума
Колебания усиливают друг друга, и результирующее движение представляет собой гармоническое колебание частоты с амплитудой (A1
+ A2).
А x
А2
А1
t
Усиление

11.

Условие интерференционного минимума:
∆= (2m + 1)·λ/2 (или ∆φ = π ± 2πт )
m = 0, 1, 2, 3, … – порядок минимума
Колебания ослабляют друг друга и результирующее
движение является гармоническим колебанием с
амплитудой |A1 – A2|. Если A1
этих точках будут отсутствовать.
= A2, то колебания в
x
А1
А
t
А2
Ослабление

12.

Стоячие волны
Стоячие волны являются частным случаем
интерференции и образуются при наложении двух
бегущих волн с одинаковыми частотами и амплитудами,
распространяющихся навстречу друг другу.
ξ1 = A·cos( t – kx) ; ξ2 = A·cos( t + kx)
ξ = ξ1 + ξ2 = 2Acoskx·cos t
2
2 Acos x cos t уравнение
стоячей волны.
2
Acт 2 Acos
x амплитуда стоячей волны.

13.

ξ
ξ
/2
x
x
Узел
Пучность
/2
Точки, в которых амплитуда колебаний максимальна (Аст
= 2А), называются пучностями стоячей волны, а точки, в
которых амплитуда колебаний равна нулю (Аст = 0),
узлами стоячей волны.
Координаты пучностей:
2
x m xпуч m (m = 0, 1, 2, …)
2
Координаты узлов:
1
1
x m x узл m
2 2
2
(m = 0, 1, 2, …)
2π