Свойства тригонометрических функций

1. У Р О К П О А Л Г Е Б Р Е

УРОК
ПО АЛГЕБРЕ
«Свойства
тригонометрических
функций»

2. Цели и задачи урока

- ознакомить учащихся со свойствами
тригонометрических функций, с понятиями
знаков, периодичности, четности и
нечетности тригонометрических функций;
- обучить учащихся определению знаков
выражения тригонометрических функций,
используя свойства тригонометрических
функций;
- развитие кругозора математических
знаний;
- воспитание сознательного отношения к
изучению данной темы

3. Актуализация опорных знаний

Что называют синусом угла ?
Что называют косинусом угла ?
Что называют тангенсом угла ?
Что называют котангенсом угла ?

4. Актуализация опорных знаний

Какой четверти
принадлежит угол
140°;
3 ;
225°,
5
3 ?

5. Объяснение нового материала

I. Знаки
тригонометрических
функций

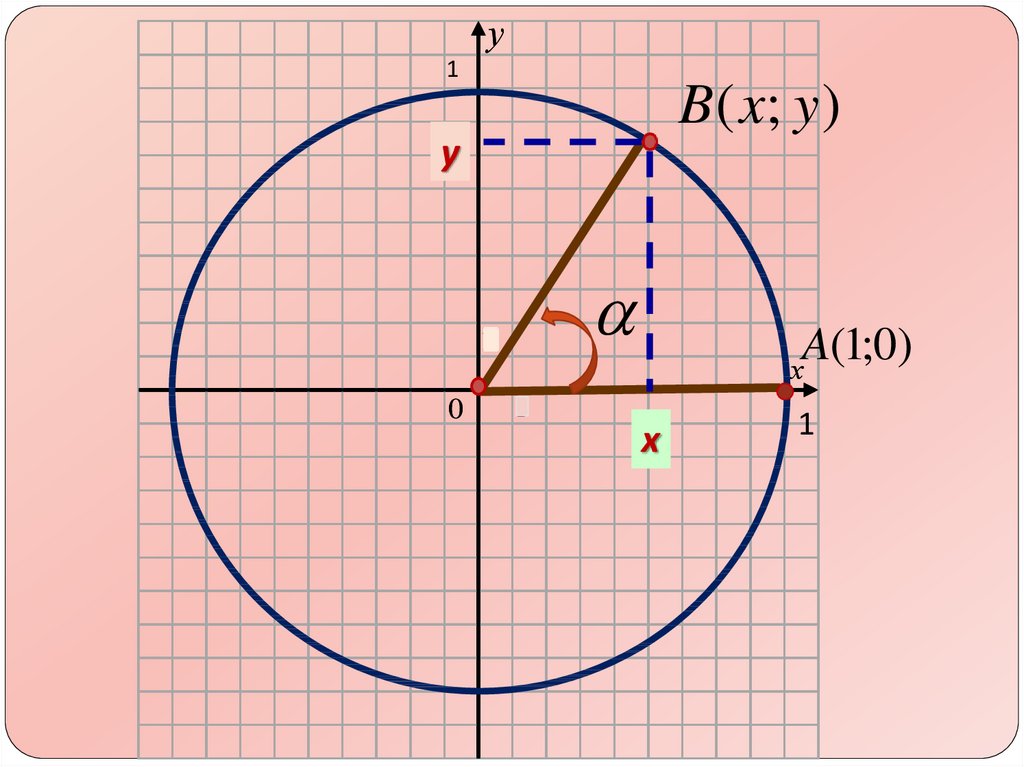
6.

у
1
B ( x; y )
у
1
0
A(1;0)
х
1
х
1

7.

у
II
1
I
1
0
III
y
sin
R
1
х
1
IV

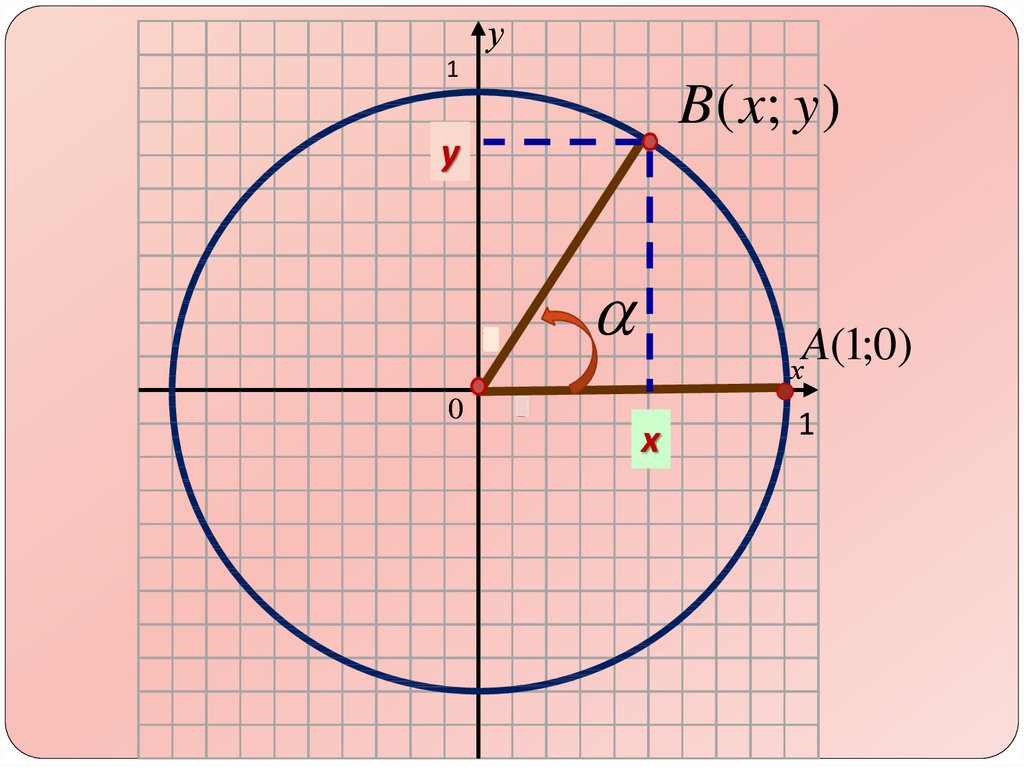
8.

у
1
B ( x; y )
у
1
0
A(1;0)
х
1
х
1

9.

у
II
1
I
1
0
III
x
cos
R
1
х
1
IV

10.

у
II
1
I
y
tg
x
1
0
х
1
1
x
ctg
y
III
IV

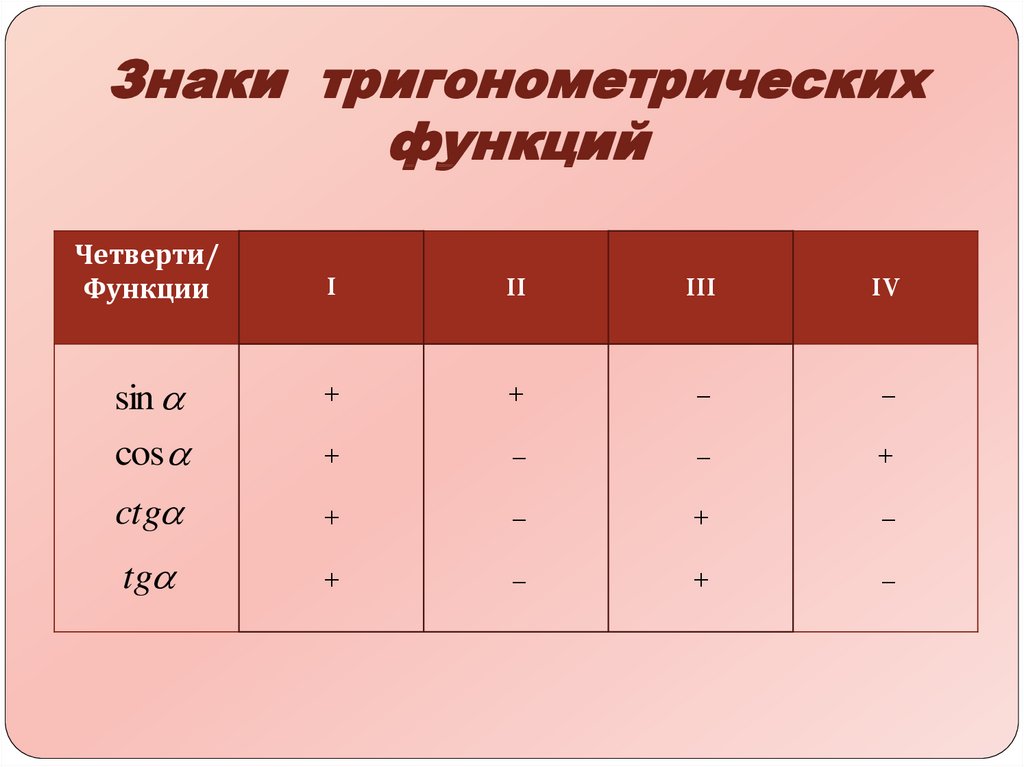
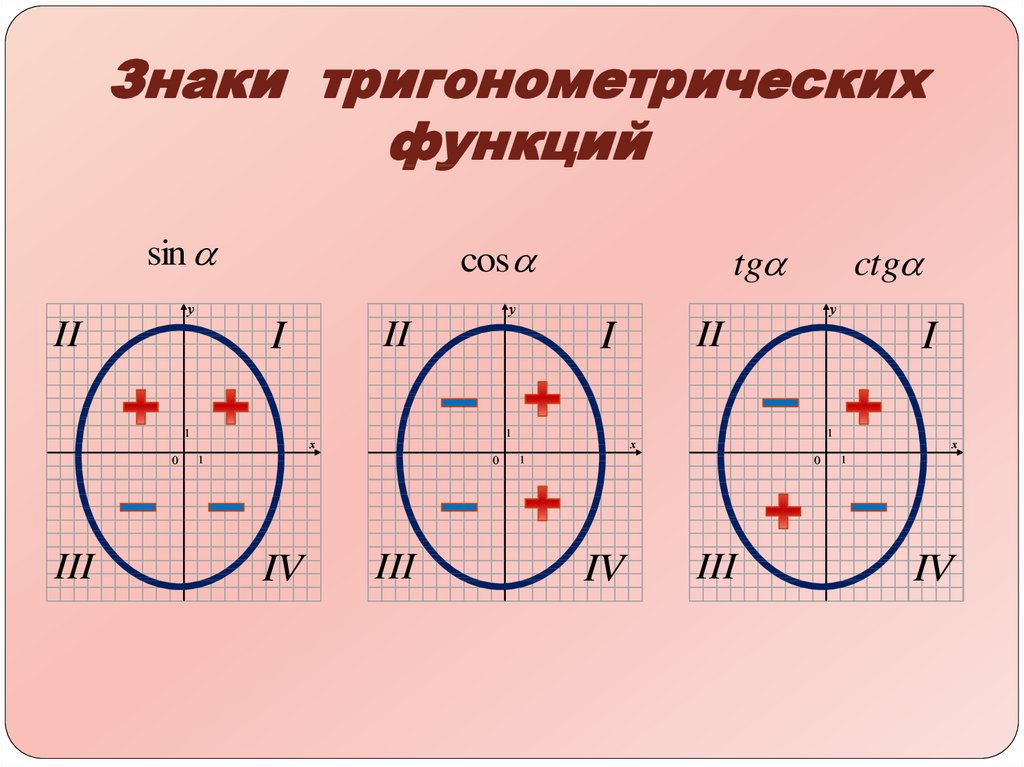
11. Знаки тригонометрических функций

Четверти/
Функции
I
II
III
IV
+
+
–
–
+
–
–
+
ctg
+
–
+
–
tg
+
–
+
–
sin
cos

12. Знаки тригонометрических функций

sin
cos
у
1
1
0
III
II
I
х
IV
у
II
I
1
III
ctg
у
II
0
tg
I
1
х
1
0
IV
III
х
1
IV

13.

II. Периодичность
тригонометрических
функций

14.

При изменении угла
на целое число оборотов
значения синуса, косинуса,
тангенса, котангенса
не изменяются

15.

sin
у
sin( 360 )
В
sin( 2 360 )
sin( n 360 )
cos
1
0
cos( 360 )
1
cos( 2 360 )
х
cos( n 360 )
A
tg
tg ( n 180 )
ctg
ctg ( n 180 )

16. Рассмотрим примеры

Найдем cos 420 ,
sin 1470 , cos1845 .
1) cos 420 cos(60 360 ) cos 60 1 ;
2
2) sin 1470 sin( 30 4 360 ) sin 30 1 ;
2
2
3) cos 1845 cos( 45 5 360 ) cos 45
.
2

17.

III. Четность и нечетность
тригонометрических
функций

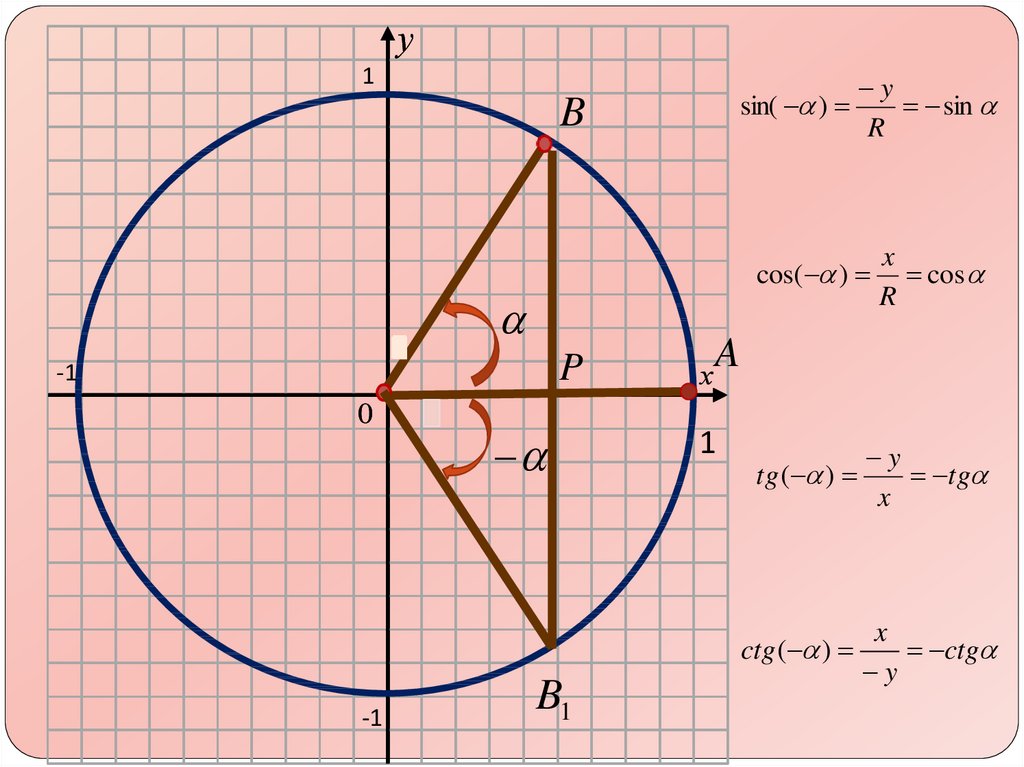
18.

у
1
sin( )
B
cos( )
1
P
-1
0
1
х
B1
x
cos
R
A
1
y
tg ( )
tg
x
ctg ( )
-1
y
sin
R
x
ctg
y

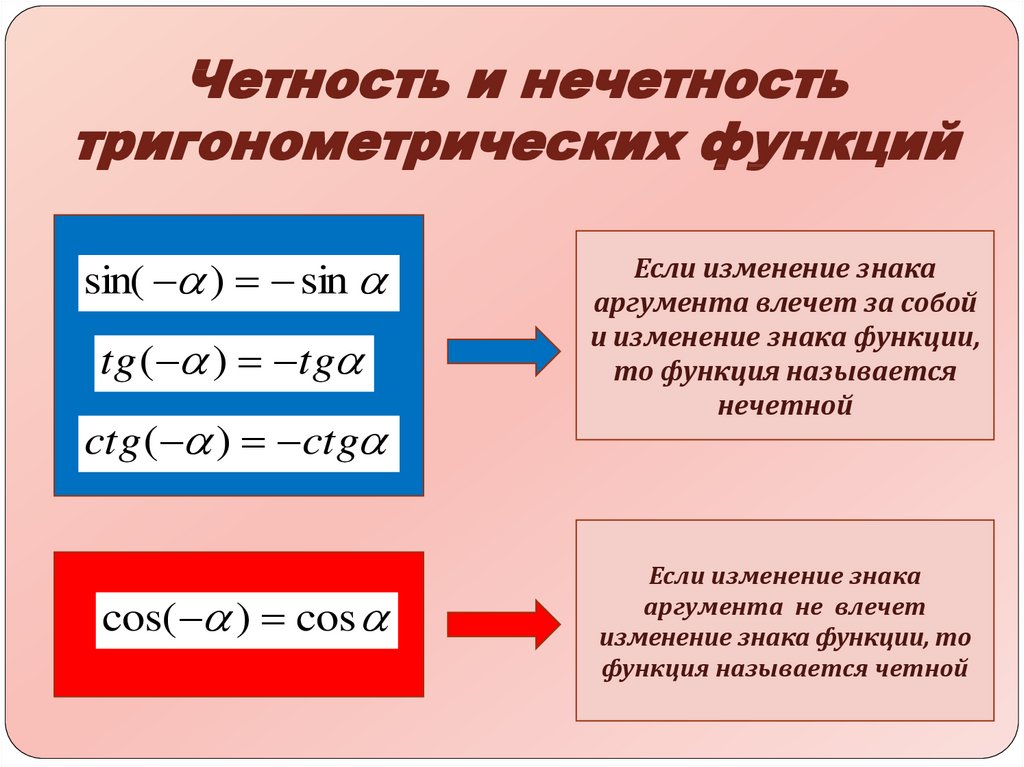
19. Четность и нечетность тригонометрических функций

sin( ) sin
tg ( ) tg
ctg ( ) ctg
cos( ) cos
Если изменение знака
аргумента влечет за собой
и изменение знака функции,
то функция называется
нечетной
Если изменение знака
аргумента не влечет
изменение знака функции, то
функция называется четной

20. Рассмотрим примеры

sin( 120 ) sin 120
cos( 160 ) cos 160
tg ( 45 ) tg 45
ctg ( 330 ) ctg330

21. Закрепление нового материала

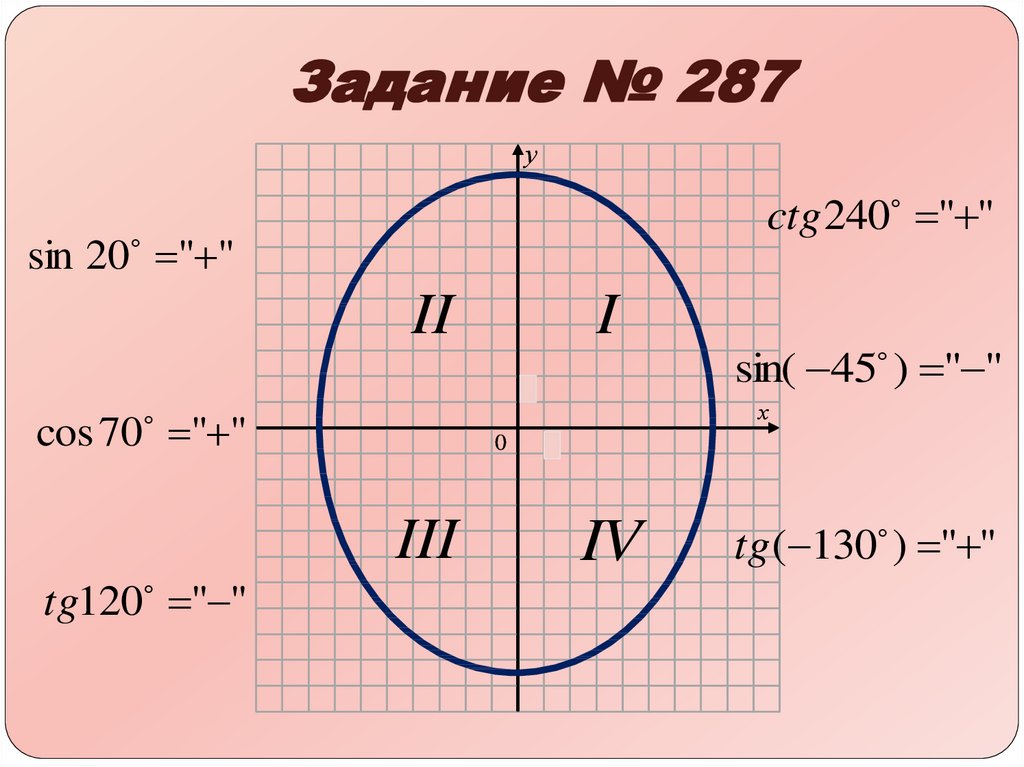
Выполнение заданий по учебнику:
№ 287 (устно),
№ 288 (устно),
№ 299 (письменно у доски),
№ 290 (письменно у доски).

22. Задание № 287

у
ctg 240 " "
sin 20 " "
II
I
1
cos 70 " "
х
0
III
tg120 " "
sin( 45 ) " "
1
IV
tg( 130 ) " "

23. Знаки тригонометрических функций

sin
cos
у
1
1
0
III
II
I
х
IV
у
II
I
1
III
ctg
у
II
0
tg
I
1
х
1
0
IV
III
х
1
IV

24. Задание № 288

у
1
0
х
1
IV

25. Задание № 288

у
1
0
III
х
1

26. Задание № 288

у
II
1
0
х
1

27. Задание № 288

у
1
0
III
х
1

28. Рефлекция

Какие знаки имеют тригонометрические
функции?
В каких четвертях имеют положительные
знаки синус, косинус, тангенс и котангенс?
В какой четверти имеют положительные
знаки все тригонометрические функции?
Какая функция является четной?
Какие функции называются нечетными?