Similar presentations:
Свойства тригонометрических функций
1. 9 класс
Свойства тригонометрическихфункций
2. Проверь себя.
3.
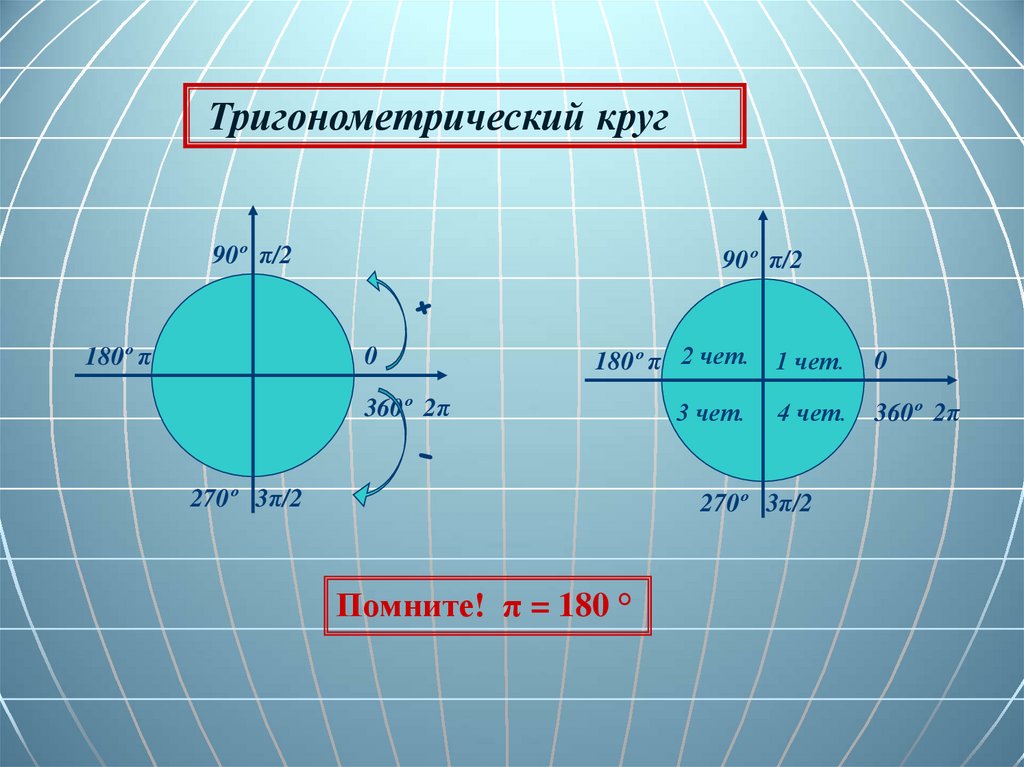
Тригонометрический круг90º π/2
180º π
90º π/2
0
180º π 2 чет. 1 чет.
360º 2π
270º 3π/2
3 чет.
4 чет.
270º 3π/2
Помните! π = 180 °
0
360º 2π
4.
Какой четвертипринадлежит угол
5. Область определения функции
Областью определенияфункции называют множество
всех допустимых значений
переменной x. Геометрически – это
проекция графика функции на ось
Ох.
6.
D(y) = RСинус, косинус
Функции непрерывны на R
Tангенс
D(y) = R, x ≠ π/2 + πn
x = π/2 + πn – вертикальная асимптота
tgx – определен при cosx ≠ 0
Котангенс
D(y) = R, x ≠ πn
x = πn – вертикальная асимптота
ctgx – определен при sinx ≠ 0
7. Множество значений функции
Множество значений функции— множество всех значений,
которые функция принимает на
области определения.
Геометрически – это проекция
графика функции на ось Оy.
8.
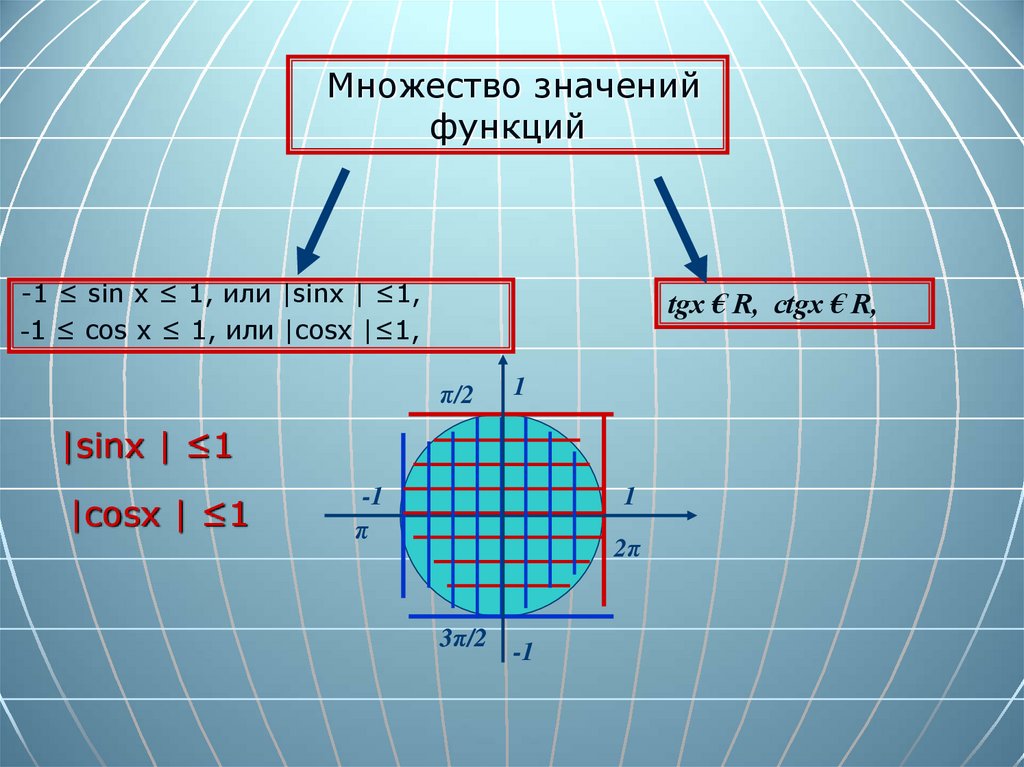
Множество значенийфункций
-1 ≤ sin х ≤ 1, или |sinx | ≤1,
-1 ≤ cos х ≤ 1, или |cosx |≤1,
tgx € R, ctgx € R,
π/2
1
|sinx | ≤1
|cosx | ≤1
-1
π
1
2π
3π/2
-1
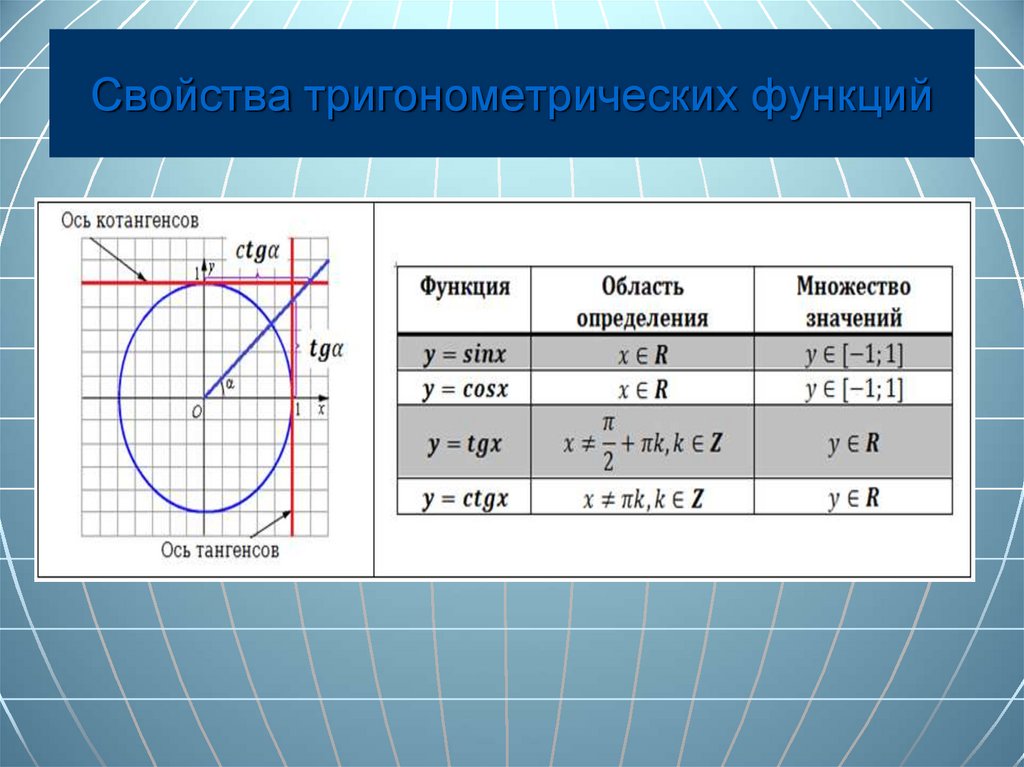
9. Свойства тригонометрических функций
10. Найди область определения функции y = 2sin(x + 3).
Найди область определения функцииy = 2sin(x + 3).
Область определения функции – это множество
всех значений аргумента, при котором
записанная формула функции имеет смысл.
Так как sinx имеет смысл при всех значений
переменной x, областью определения функции
y = 2sin(x + 3) является вся
числовая прямая, т.е. (–∞; +∞).
11. Найди сумму всех целых значений функции y = – 6 cosx + 1.
Найди сумму всех целых значенийфункции y = – 6 cosx + 1.
Решение. Так как множество значений
функции y = cosx – промежуток [–1; 1], тогда:
–1 ≤ cosx ≤ 1,
–6 ≤ –6cosx ≤ 6,
–5 ≤ –6cosx + 1 ≤ 7,
т.е. множество значений функции y = –6cosx + 1 –
промежуток [–5; 7]. Этому промежутку
принадлежат следующие целые числа:
–5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, 6, 7.
Найди сумму этих чисел:
(–5) + (–4) + (–3) + (–2) + (–1) + 0 + 1 + 2 + 3 +
4 + 5 + 6 + 7 = 13.
Ответ: 13.
12. Найди область значений функции y = 2cosx.
Найди область значений функции y = 2cosx.Так как множество значений
функции y = cosx – промежуток
[–1; 1], тогда:
–1 ≤ cosx ≤ 1,
–2 ≤ 2cosx ≤ 2,
т.е. множество значений функции
y = 2cosx – промежуток [–2; 2].
13.
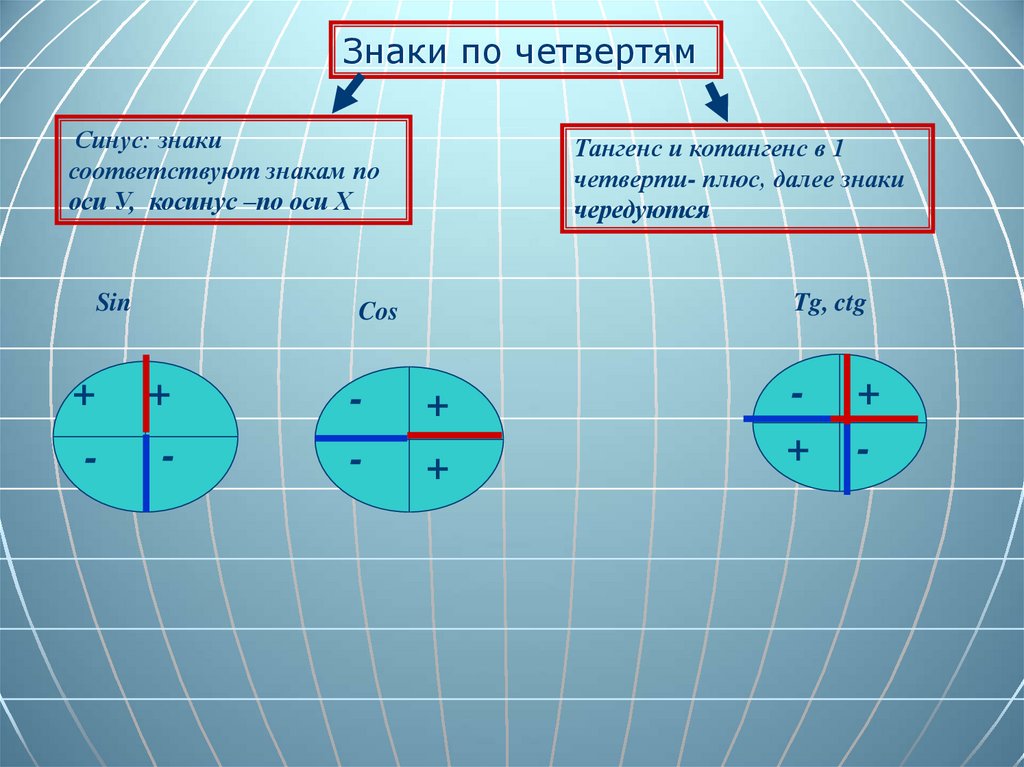
Знаки по четвертямСинус: знаки
соответствуют знакам по
оси У, косинус –по оси Х
Sin
Тангенс и котангенс в 1
четверти- плюс, далее знаки
чередуются
Tg, ctg
Cos
+
+
-
-
-
+
+
+
+
-
14. Рассмотрим примеры
уctg 240 " "
sin 20 " "
II
I
1
cos 70 " "
х
0
III
tg120 " "
sin( 45 ) " "
1
IV
tg( 130 ) " "
15. Четность и нечетность тригонометрических функций
sin( ) sintg ( ) tg
ctg ( ) ctg
cos( ) cos
Если изменение знака
аргумента влечет за
собой и изменение
знака функции, то
функция называется
нечетной
Если изменение знака
аргумента не влечет
изменение знака
функции, то функция
называется четной
16.
нечетныеСинус, тангенс, котангенс –функции
Минус у угла можно вынести за знак функции
Косинус – функция
четная
Минус у угла можно опустить
Примеры
1. sin ( – х) = - sin х
2. sin ( π/4 – х) =
-
sin ( х - π/4 )
3. tg (- π/6) = - tg π/6 = -
3
3
4. cos (-7π/3)= cos 7π/3 = cos (2π + π/3) = cos π/3 = ½
5. cos (-β) = cos β
6. ctg ( 2α - π/2) = - ctg (π/2 - 2α )
17. Рассмотрим примеры
cos (-120 )= cos 120sin (-120 )=- sin 120
tg (-45 )=-tg 45
сtg (-60 )=-сtg 60
18.
Периодэто число,
при прибавлении
f(x +Т)
которого к аргументу значение функции не
изменяется.
Если Т – период, то Tn для n € Z тоже период.
–
=f(x)
Считается Т – наименьший период
Так как
sin, cos
f(x +Тn) = f(x),
Т=2π
то Tn можно опустить
tg, ctg
Примеры
1. sin 390º = sin (360º + 30º) = sin 30º = ½
2. sin 790º = sin (2∙360º + 30º) = sin 30º = ½
3
3. tg 210º = tg (180º + 30º) = tg 30º = 3
4. cos 7π/3= cos (2π + π/3) = cos π/3 = ½
5. cos (2π – β) = cos (-β) = cos β
6. sin (6π – 2α) = sin (-2α) = - sin 2α
Т=π
19. Рассмотрим примеры
Найдем1)
cos 420 ,
cos1845 .
sin 1470 ,
1
cos 420 cos(60 360 ) cos 60 ;
2
2)
1
sin 1470 sin( 30 4 360 ) sin 30 ;
2
3)
2
cos 1845 cos( 45 5 360 ) cos 45
.
2
















 mathematics
mathematics








