Similar presentations:
Тригонометрия. Единичная окружность. Определение синуса и косинуса угла. Тригонометрические тождества и формулы
1. Тригонометрия
1у
у
1 М
М
N
-1
K
0
P-1
А
1 x
-1
N
0
K
-1 P
А
1 x
2. Содержание
Единичная окружностьОпределение синуса и косинуса угла
Тригонометрические тождества
Тригонометрические формулы
3. Единичная окружность
Единичная окружностьОткладывание произвольных углов
Полный оборот
Радианная мера угла
Перевод градусной меры в радианную
Перевод радианной меры в градусную
4. Единичная окружность
N-1
1
y
M +
0
1
K
−
-1
P
x
5. Откладывание углов
yK(– 240о)
N(150о)
P(– 45о)
M(210о)
K
+
А
N
-1
1
0
M
P
-1
−
А(30о)
1
x
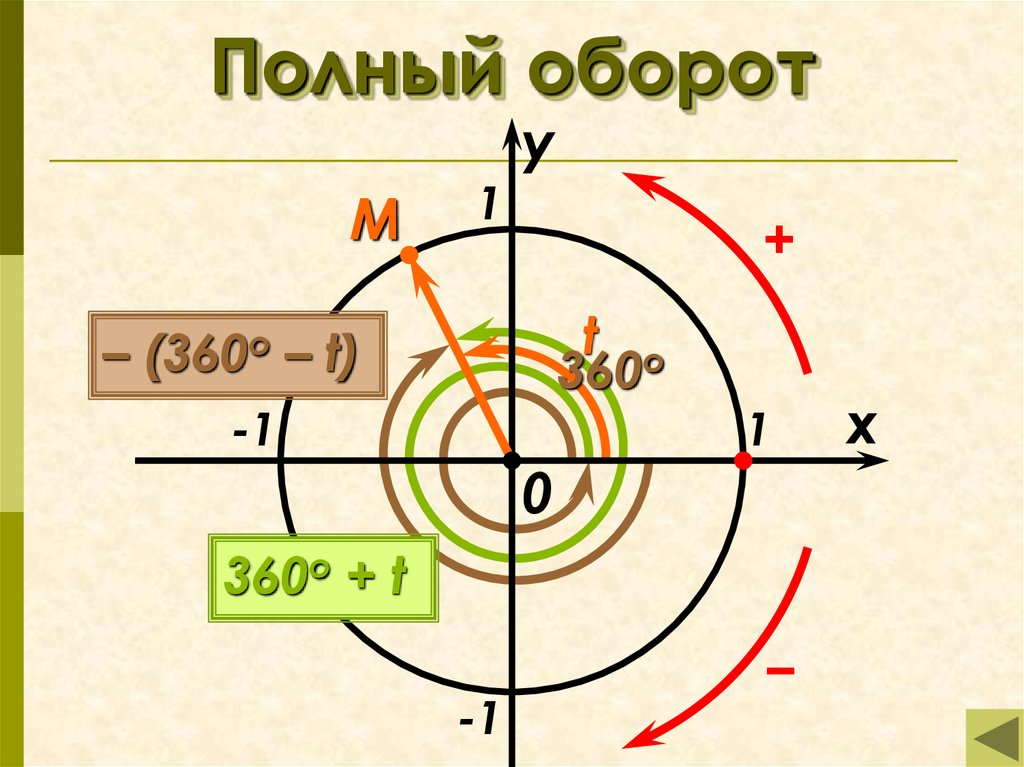
6. Полный оборот
M1
y
+
t o
360
– (360o – t)
-1
1
0
360o + t
−
-1
x
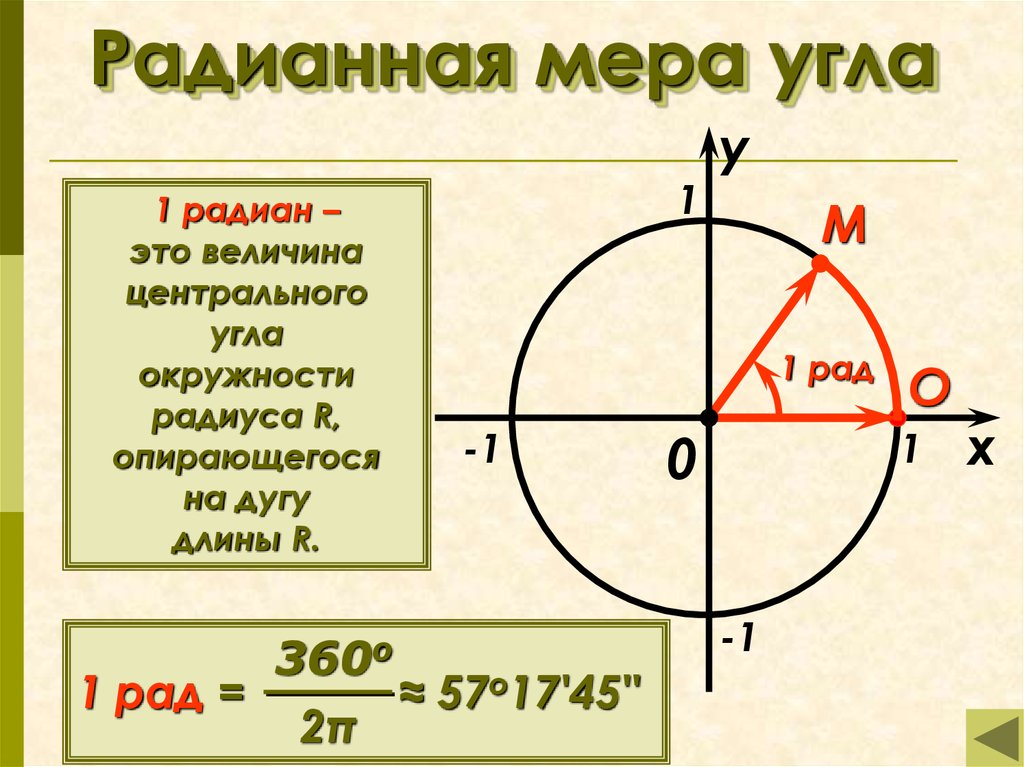
7. Радианная мера угла
1 радиан –это величина
центрального
угла
окружности
радиуса R,
опирающегося
на дугу
длины R.
1 рад =
360о
2π
1
y
M
1 рад
-1
0
1
-1
≈ 57о17'45''
О
x
8. Перевод градусной меры в радианную
π=
рад
180o
π
π
o
о
30 = 30
=
рад
180o
6
π
2π
o
о
120 = 120
=
рад
180o
3
π
5π
o
о
− 75 = − 75
=
−
рад
180o
12
to
tо
9.
Перевод радианноймеры в градусную
t рад = t
o
180
π
π
π 180o
рад = ∙ π = 60о
3
3
3π
3π 180o
рад = ∙ π = 135о
4
4
2π
2π 180o
о
–
рад = –
∙
= – 40
9
9 π
10. Определение синуса и косинуса
Определение синуса и косинусаОпределение тангенса и котангенса
Знаки синуса и косинуса,
Знаки тангенса и котангенса
Расположение табличных углов на единичной
окружности
Расположение углов с шагом 30° на единичной
окружности
Расположение углов с шагом 45° на единичной
окружности
Свойства четности и нечетности
Таблица значений тригонометрических функций
11.
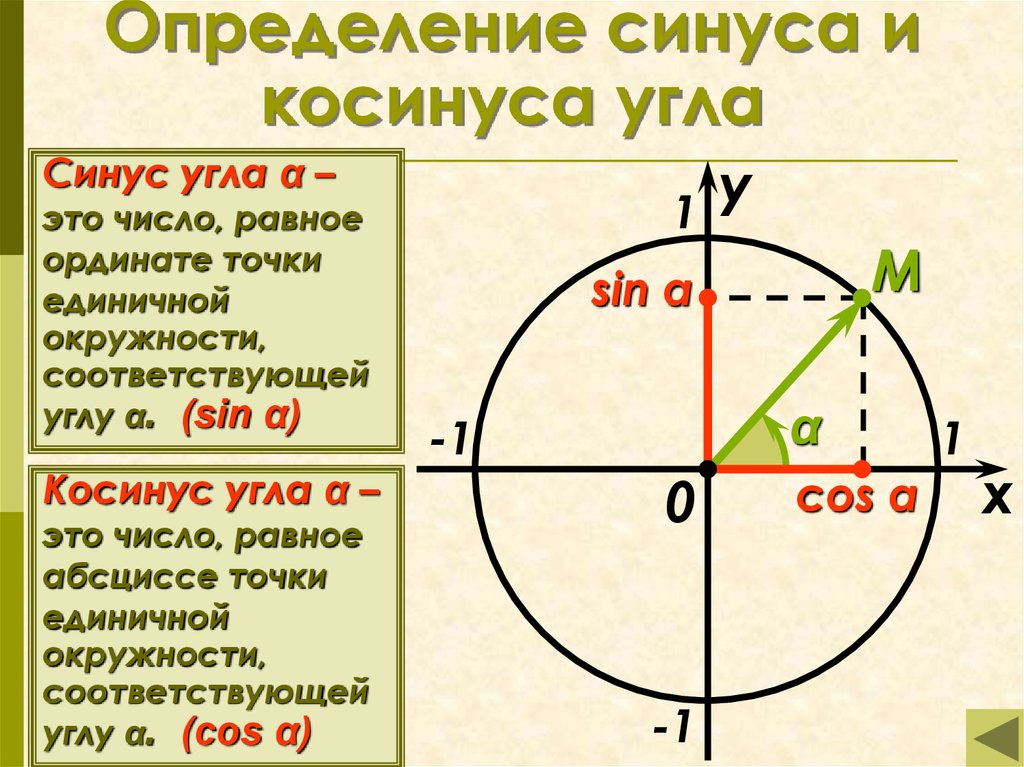
Определение синуса икосинуса угла
Синус угла α –
это число, равное
ординате точки
единичной
окружности,
соответствующей
углу α. (sin α)
Косинус угла α –
это число, равное
абсциссе точки
единичной
окружности,
соответствующей
углу α. (cos α)
y
1
M
sin α
α
-1
0
-1
cos α
1
x
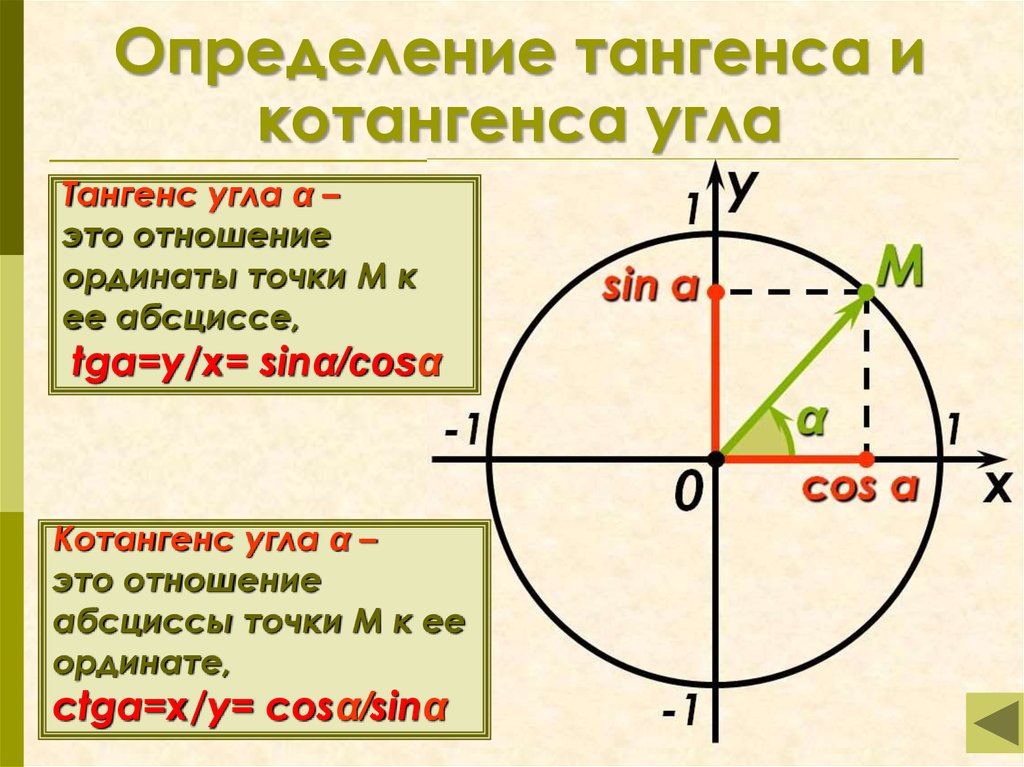
12.
Определение тангенса икотангенса угла
Тангенс угла α –
это отношение
ординаты точки М к
ее абсциссе,
tgα=y/x= sinα/cosα
Котангенс угла α –
это отношение
абсциссы точки М к ее
ординате,
ctgα=x/y= cosα/sinα
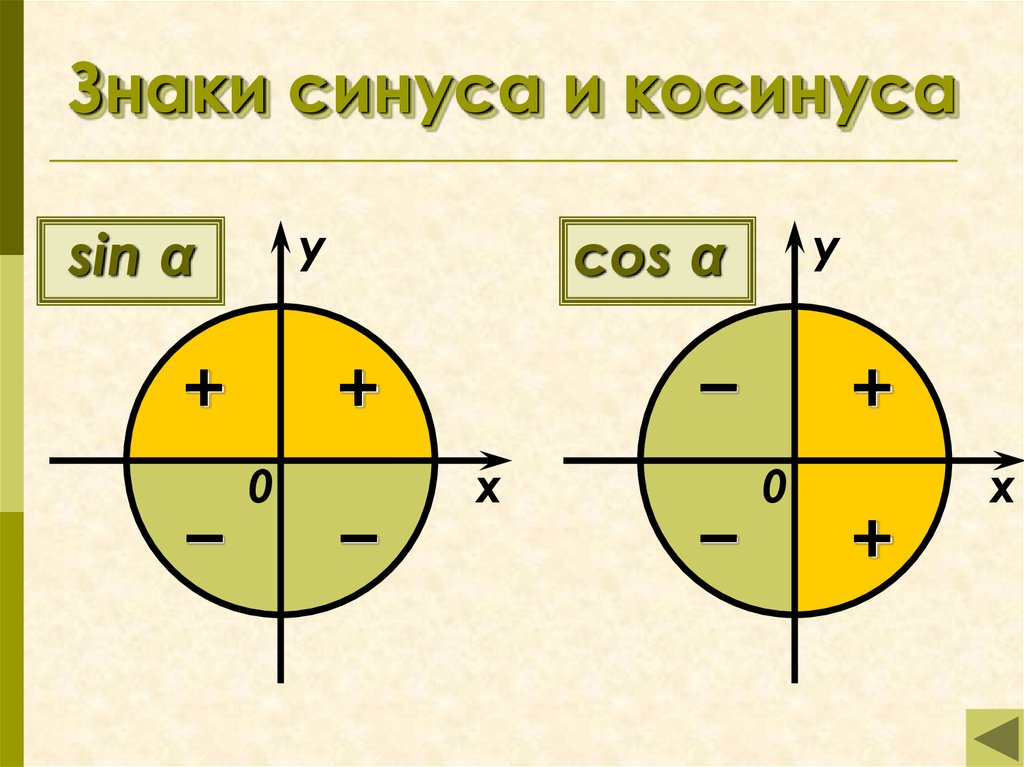
13. Знаки синуса и косинуса
уsin α
+
−
+
0
у
соs α
−
−
x
−
+
0
+
x
14. Знаки тангенса и котангенса
уtg α
+
−
+
0
у
ctg α
−
−
x
+
+
0
−
x
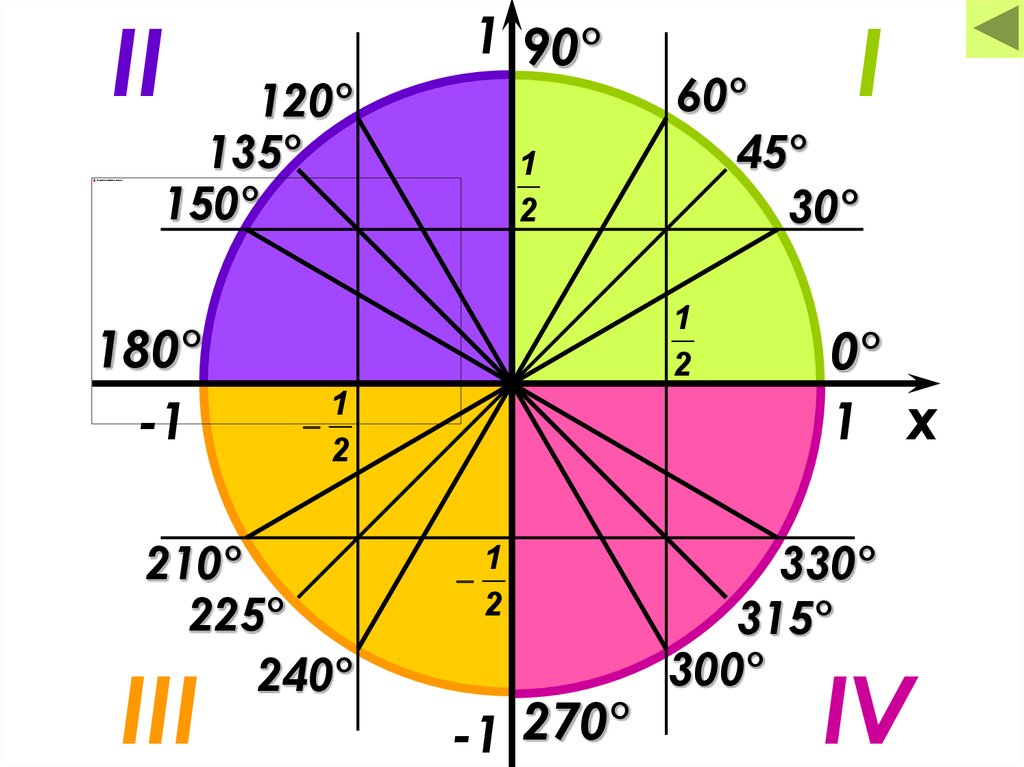
15.
II120°
135°
150°
180°
-1
1
2
I
60°
45°
30°
1
2
1
2
210°
225°
240°
III
1 90°
1
2
-1 270°
0°
1 x
330°
315°
300°
IV
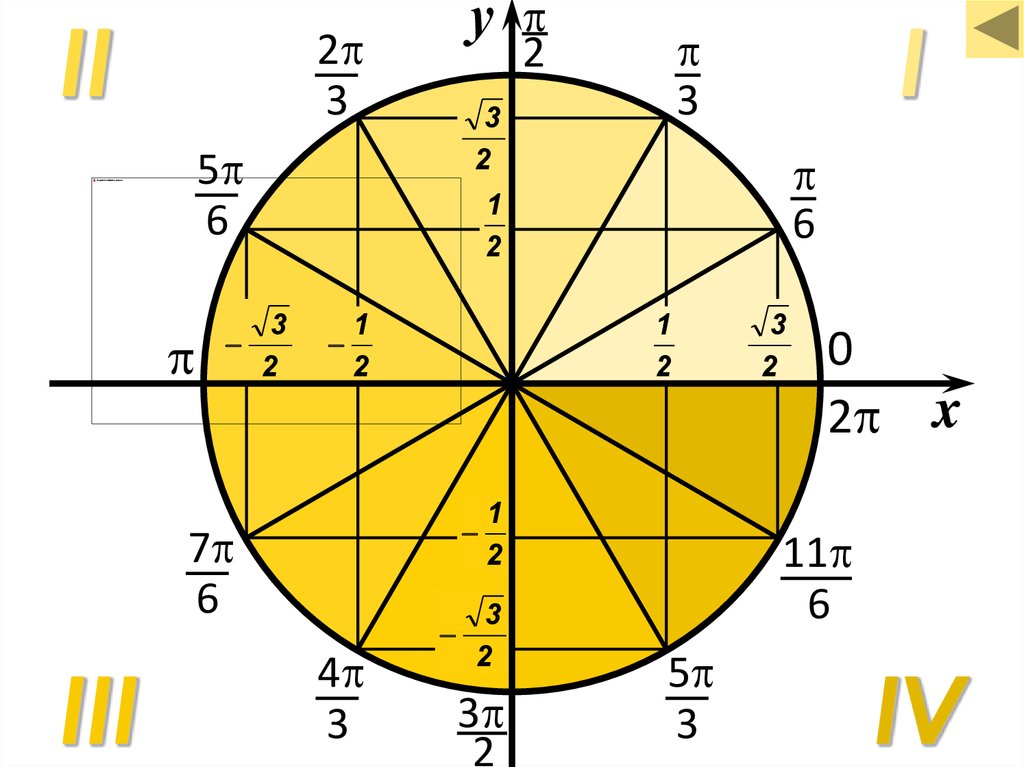
16.
II2
3
5
6
3
2
I
3
2
3
2
6
1
2
1
2
1
2
1
2
7
6
III
у
4
3
3
2
3
2
3
2
0
2
x
11
6
5
3
IV
17.
уII
3
4
III
I
2
2
2
2
2
5
4
4
2
2
2
2
3
2
7
4
0
2
x
IV
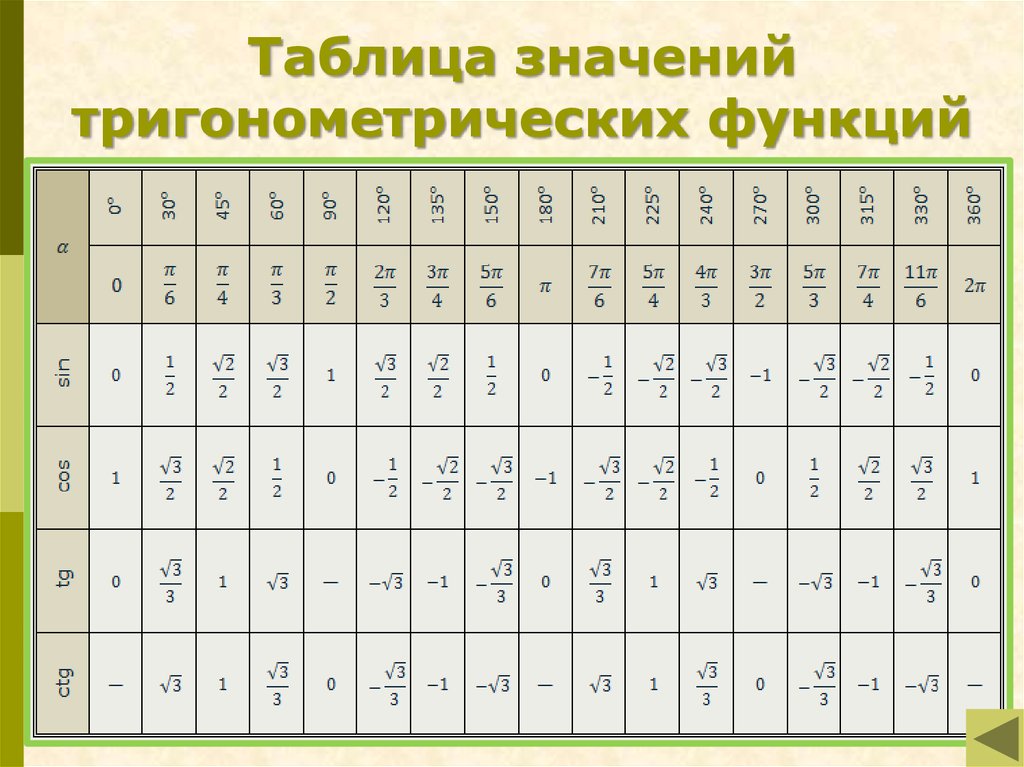
18.
Таблица значенийтригонометрических функций
19. Свойства четности и нечетности
cos(− α) = cos αчетная
M
1
y
sinα
α
-1
sin(− α) = − sin α
нечетная
cosα
0
−α
M1
−sinα
-1
x
1
20. Тригонометрические тождества
Основное тригонометрическое тождество (1)Тригонометрическое тождество (2)
Тригонометрическое тождество (3)
Тригонометрическое тождество (4)
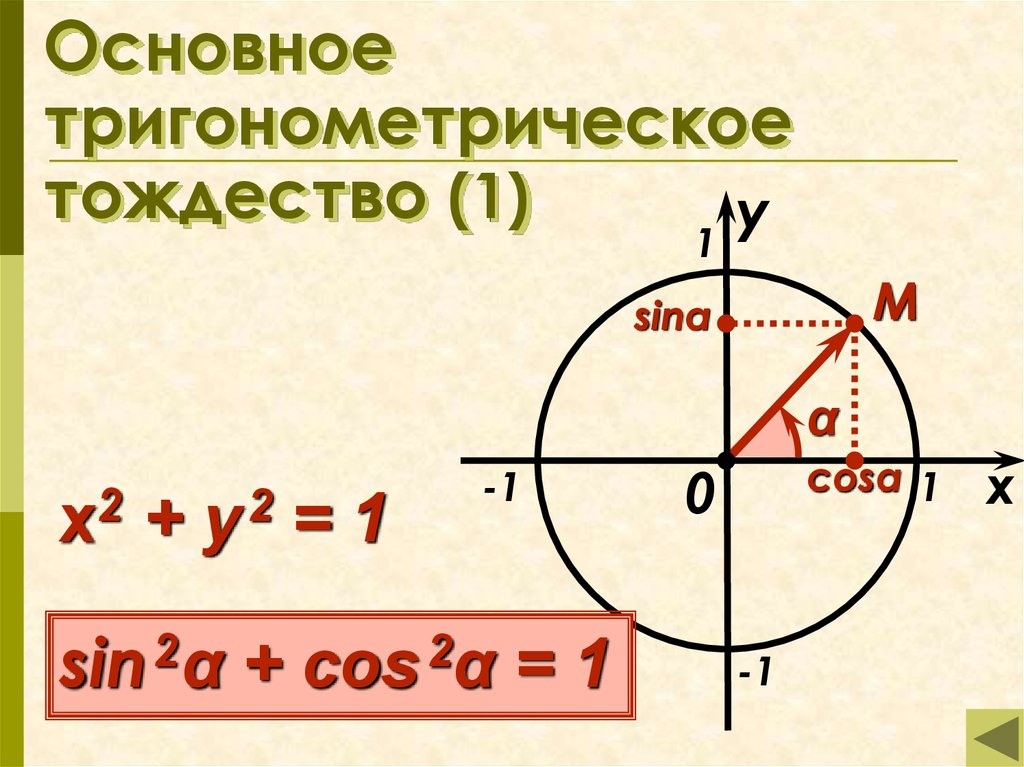
21. Основное тригонометрическое тождество (1)
y1
M
sinα
α
2
x
+
2
y
=1
-1
sin 2α + cos 2α = 1
cosα 1
0
-1
x
22. Тригонометрическое тождество (2)
sin2α+
cos2α
=1
:
2
cos α
sin2α cos2α
1
+
=
2
2
2
cos α cos α cos α
1
tg2α + 1 =
cos2α
23. Тригонометрическое тождество (3)
sin2α+
cos2α
=1
:
2
sin α
sin2α cos2α
1
+
=
2
2
2
sin α sin α
sin α
1
1 + ctg2α =
sin2α
24. Тригонометрическое тождество (4)
tgα x ctgα = 1sinα
cosα
x
=1
cosα
sinα
25. Тригонометрические формулы
Формулы приведения (правило)Формулы приведения (таблица)
Формулы сложения
Формулы суммы и разности синусов (косинусов)
Формулы двойного аргумента
Формулы половинного аргумента
Формулы преобразования произведения в сумму
26. ФОРМУЛЫ ПРИВЕДЕНИЯ (ПРАВИЛО)
УФОРМУЛЫ ПРИВЕДЕНИЯ
(ПРАВИЛО)
2
Х
0
2
3
2
Приведение через
«рабочие»
углы:
3 5
2
Название
функции
Знак
;
2
;
2
; ...
Меняется на
конфункцию
Приведение через
«спящие» углы:
; 2 ; 3 ; ...
Не меняется
Определяется по знаку функции в
левой части формулы
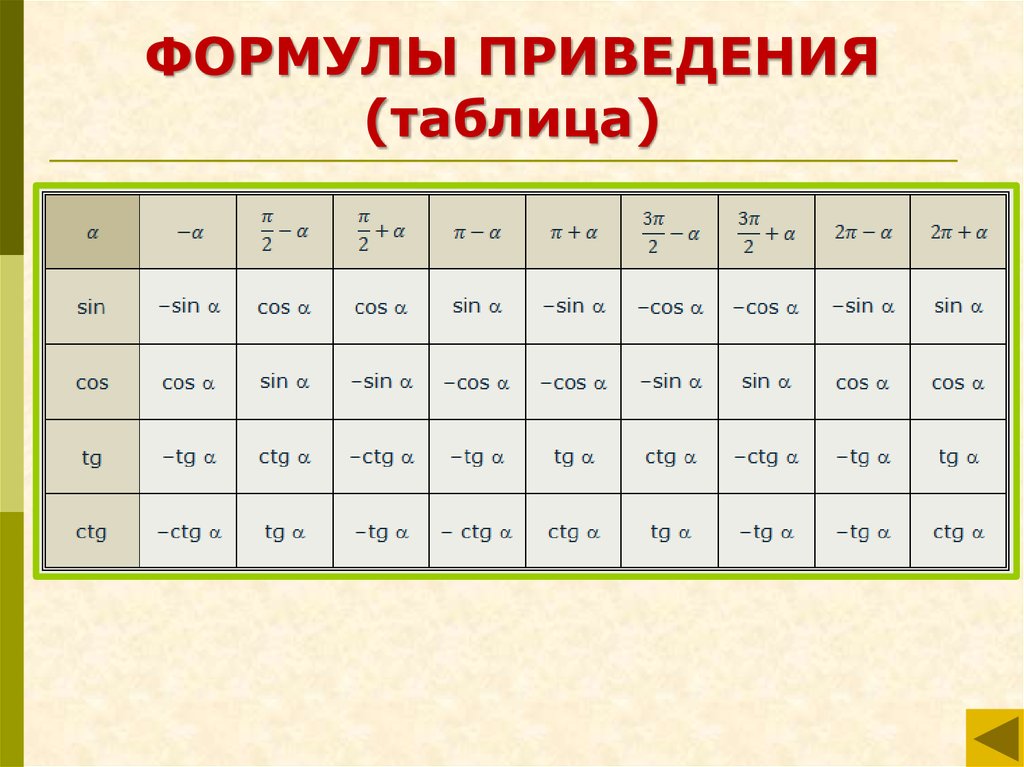
27.
ФОРМУЛЫ ПРИВЕДЕНИЯ(таблица)
28.
Формулы сложенияcos( ) cos cos sin sin
cos( ) cos cos sin sin
sin( ) sin cos cos sin
sin( ) sin cos cos sin
tg tg
tg ( )
1 tg tg
29.
Формулы суммы и разностиsin sin 2 sin
cos
2
2
sin sin 2 sin
cos
2
2
cos cos 2 cos
cos
2
2
cos cos 2 sin
sin
2
2
30.
Формулы суммы и разности31.
Формулы двойного аргументаsin 2 2sin cos
cos 2 cos sin
2
2
cos 2 1 2sin
2
cos 2 2 cos 1
2
2tg
tg 2
2
1 tg
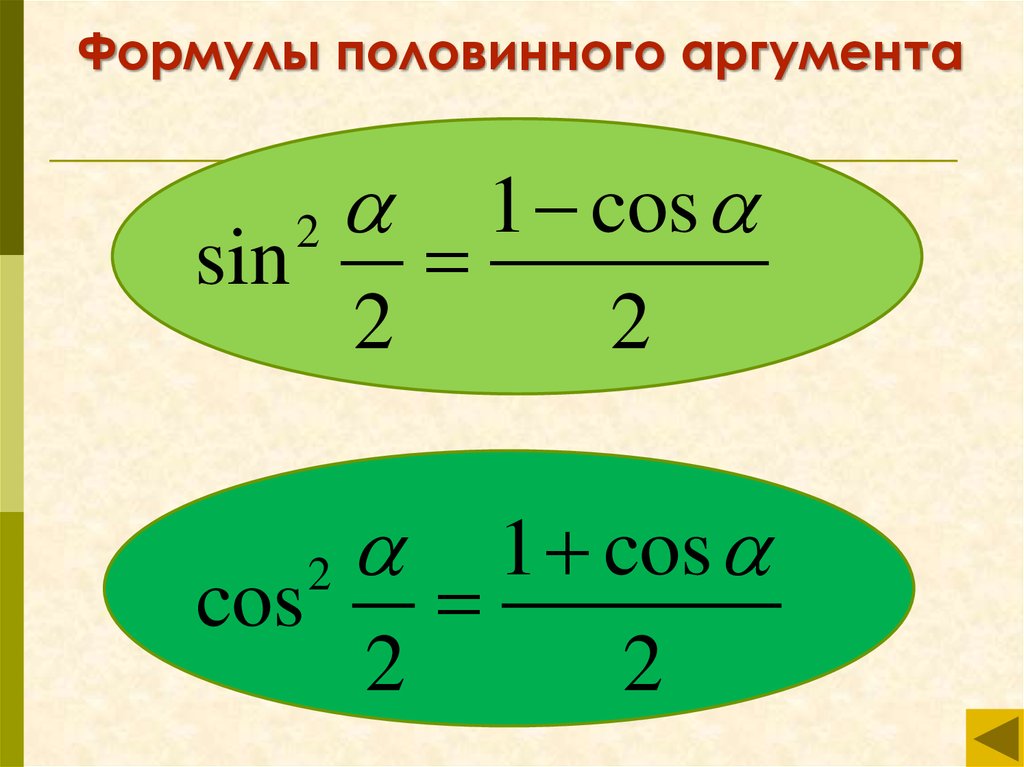
32.
Формулы половинного аргумента1 cos
sin
2
2
2
1 cos
cos
2
2
2
33.
Формулы преобразованияпроизведения в сумму






















 mathematics
mathematics