Свойства тригонометрических функций

1. Свойства тригонометрических функций

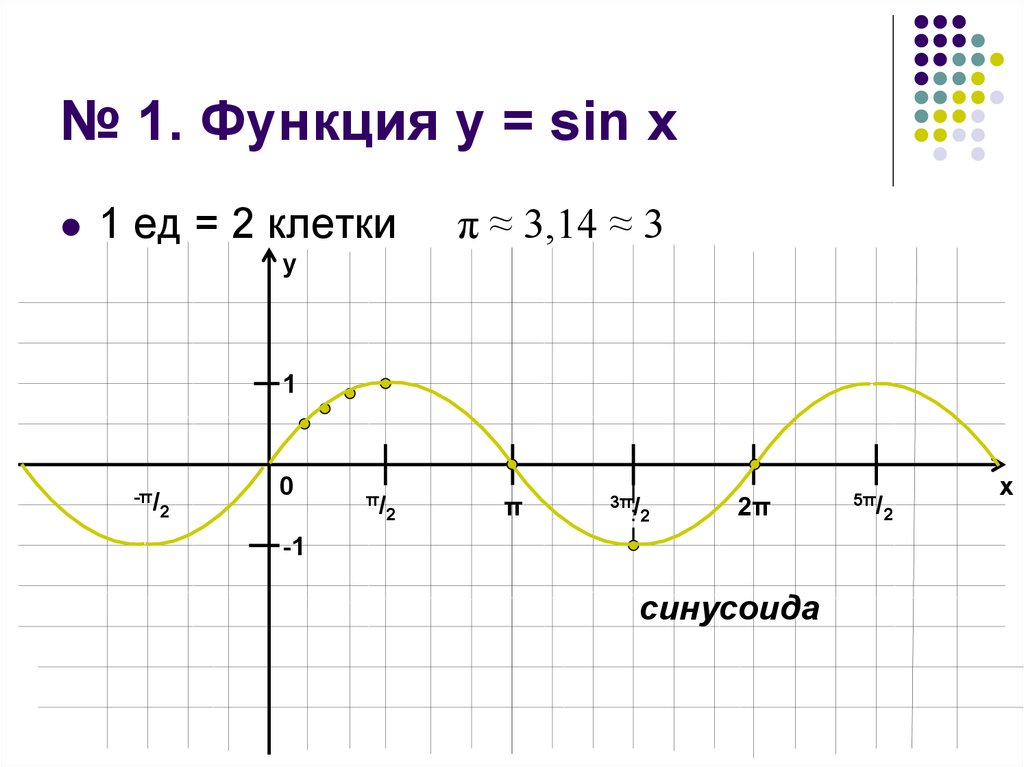
2. № 1. Функция у = sin x

1 ед = 2 клетки
π ≈ 3,14 ≈ 3
у
1
-π/
0
2
π/
2
π
3π/
2
2π
-1
синусоида
5π/
х
2

3. № 1. Функция у = sin х.

1. Область определения
D(f) = (–∞; +∞) = R
2. Область значений
Е(f) = [–1; 1]
3. Точки пересечения с осями координат
Ох: x = πn, nЄZ
Оу: y = 0

4. № 1. Функция у = sin х.

4. Промежутки знакопостоянства функции
f(х)>0 при хЄ(2πn; π + 2πn), nЄZ
f(х)<0 при хЄ(π + 2πn; 2π + 2πn), nЄZ
5. Точки экстремума функции
x = π/2 + 2πn, nЄZ – точки max
3
x = π/2 + 2πn, nЄZ – точки min
6. Промежутки монотонности функции
f(х)↑ при хЄ(–π/2 + 2πn; π/2 + 2πn), nЄZ
3
f(х)↓ при хЄ(π/2 + 2πn; π/2 + 2πn), nЄZ

5. № 1. Функция у = sin х.

7. Периодичность функции
Т = 2π
8. Четность (нечетность) функции
Нечетная, т.к. график симметричен
относительно начала координат

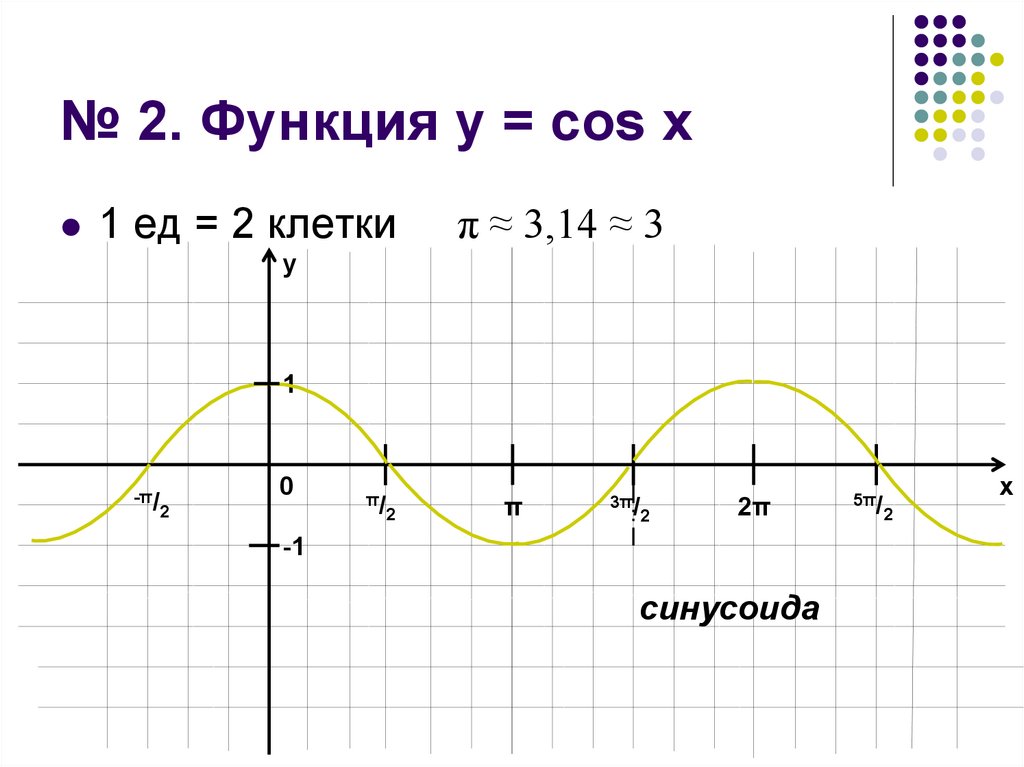
6. № 2. Функция у = cos x

1 ед = 2 клетки
π ≈ 3,14 ≈ 3
у
1
-π/
0
2
π/
2
π
3π/
2
2π
-1
синусоида
5π/
х
2

7. № 2. Функция у = cos х.

1. Область определения
D(f) = (–∞; +∞) = R
2. Область значений
Е(f) = [–1; 1]
3. Точки пересечения с осями координат
Ох: x = π/2 + πn, nЄZ
Оу: y = 1

8. № 2. Функция у = cos х.

4. Промежутки знакопостоянства функции
f(х)>0 при хЄ(–π/2 + 2πn; π/2 + 2πn), nЄZ
f(х)<0 при хЄ(π/2 + 2πn; 3π/2 + 2πn), nЄZ
5. Точки экстремума функции
x = 0 + 2πn = 2πn, nЄZ – точки max
x = π + 2πn, nЄZ – точки min
6. Промежутки монотонности функции
f(х)↑ при хЄ(–π + 2πn; 2πn), nЄZ
f(х)↓ при хЄ(2πn; π + 2πn), nЄZ

9. № 2. Функция у = cos х.

7. Периодичность функции
Т = 2π
8. Четность (нечетность) функции
Функция четная, т.к. график симметричен
относительно Оу.

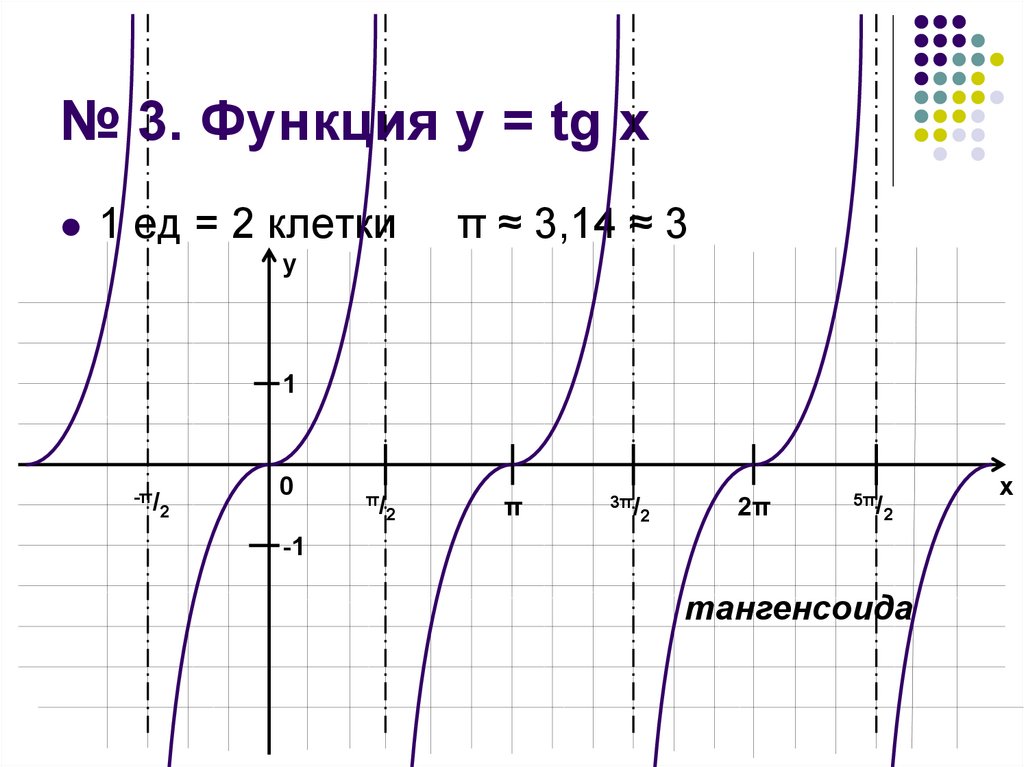
10. № 3. Функция у = tg x

1 ед = 2 клетки
π ≈ 3,14 ≈ 3
у
1
-π/
0
2
π/
2
π
3π/
2
2π
5π/
х
2
-1
тангенсоида

11. № 3. Функция у = tg х.

1. Область определения
D(f) = (–π/2 + πn; π/2 + πn), nЄZ
2. Область значений
Е(f) = (–∞; +∞) = R
3. Точки пересечения с осями координат
Ох: x = 0 + πn = πn, nЄZ
Оу: y = 0

12. № 3. Функция у = tg х.

4. Промежутки знакопостоянства функции
f(х)>0 при хЄ(πn; π/2 + πn), nЄZ
f(х)<0 при хЄ(–π/2 + πn; πn), nЄZ
5. Точки экстремума функции
точек экстремума нет
6. Промежутки монотонности функции
возрастает при всех значениях области
определения

13. № 3. Функция у = tg х.

7. Периодичность функции
Т=π
8. Четность (нечетность) функции
Нечетная, т.к. график симметричен
относительно начала координат.

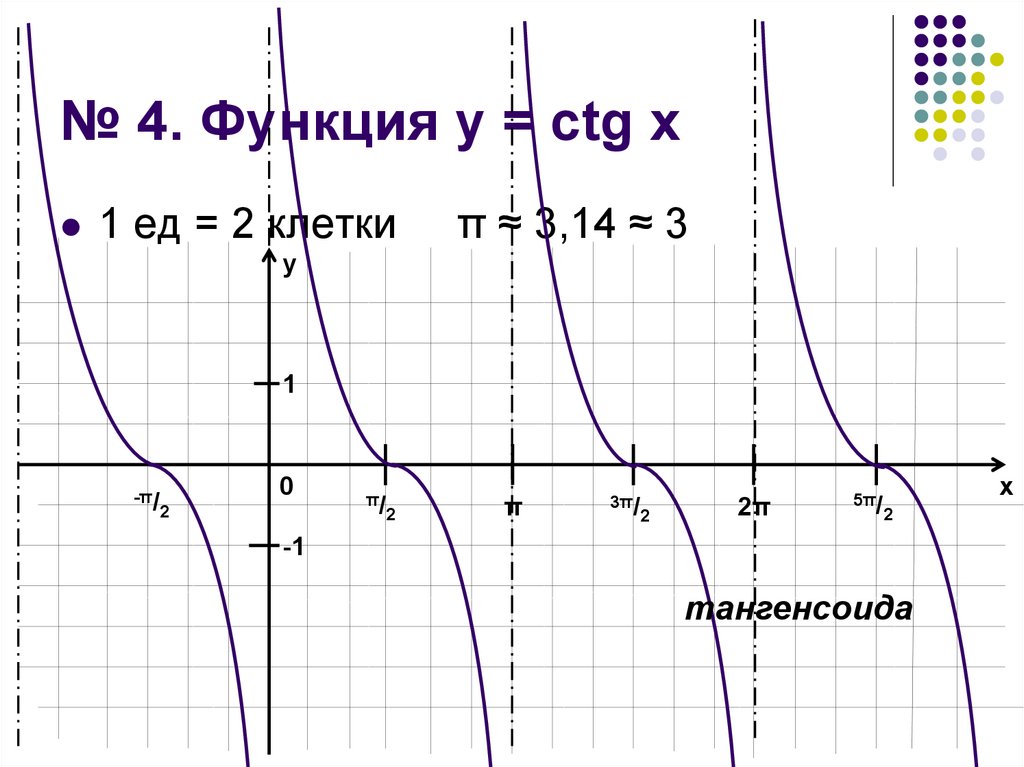
14. № 4. Функция у = ctg x

1 ед = 2 клетки
π ≈ 3,14 ≈ 3
у
1
-π/
0
2
π/
2
π
3π/
2
2π
5π/
х
2
-1
тангенсоида

15. № 4. Функция у = ctg х.

1. Область определения
D(f) = (πn; π + πn), nЄZ
2. Область значений
Е(f) = (–∞; +∞) = R
3. Точки пересечения с осями координат
Ох: x = π/2 + πn, nЄZ
Оу: точек пересечения нет

16. № 4. Функция у = ctg х.

4. Промежутки знакопостоянства функции
f(х)>0 при хЄ(πn; π/2 + πn), nЄZ
f(х)<0 при хЄ(π/2 + πn; π + πn), nЄZ
5. Точки экстремума функции
точек экстремума нет
6. Промежутки монотонности функции
убывает при всех значениях области
определения

17. № 4. Функция у = ctg х.

7. Периодичность функции
Т=π
8. Четность (нечетность) функции
Нечетная, т.к. график симметричен
относительно начала координат