Определение и знаки тригонометрических функций

1. Определение и знаки тригонометрических функций

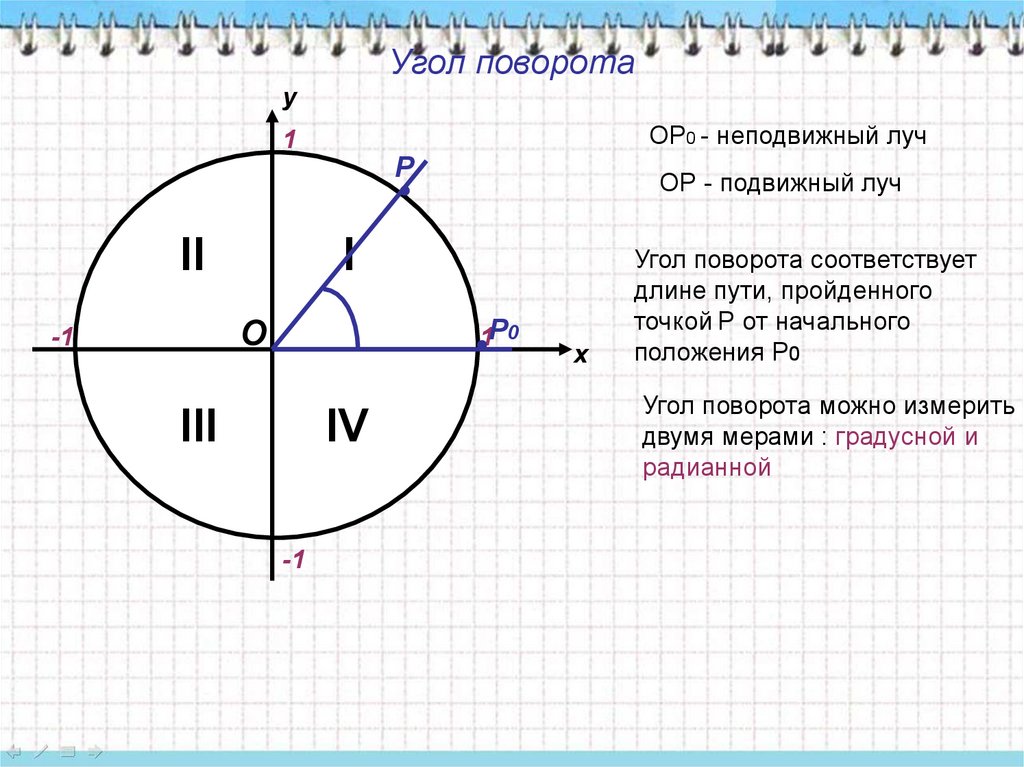
2. Угол поворота

у
ОР0 - неподвижный луч
1
II
Р
I
1Р0
О
-1
ОР - подвижный луч
III
IV
-1
х
Угол поворота соответствует
длине пути, пройденного
точкой Р от начального
положения Р0
Угол поворота можно измерить
двумя мерами : градусной и
радианной

3. Окружность с центром в начале системы координат Oxy и радиусом, равным единице, называется единичной, а ограниченный ей круг –

тригонометрическим.
• Приняв точку пересечения
окружности с
положительной частью оси
Ох за начало отсчета;
• Выбрав положительное
направление – против
часовой стрелки,
отрицательное – по
часовой стрелке;
• Отложив от начала
отсчета дугу в 1 рад, мы
получим, что
тригонометрическая
окружность в некотором
смысле «эквивалентна»
понятию «числовая
прямая».
y
1
1
«+»
0
0
1
« »
x

4. Тригонометрические функции

Определение. Тригонометрические функции - это
неалгебраические функции, устанавливающие
зависимость между сторонами и углами треугольника.
Тригонометрические функции угла α определяются при
помощи числовой окружности, а также из
прямоугольного треугольника (для острых углов).

5. Определение синуса

• Синусом угла х называется ордината точки,
полученной поворотом точки (1; 0) вокруг начала
координат на угол х (обозначается sin x).
sin x
x
(1;0)

6. Определение косинуса

• Косинусом угла х называется абсцисса точки,
полученной поворотом точки (1; 0) вокруг начала
координат на угол х (обозначается cos x).
x
cos x
(1;0)

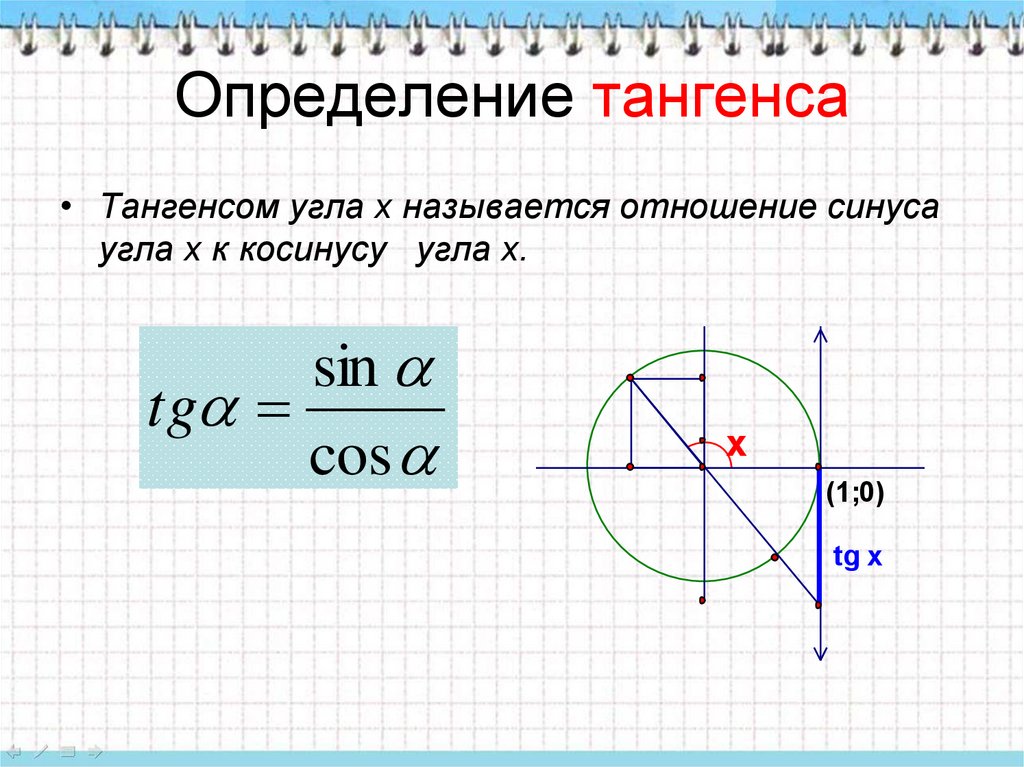
7. Определение тангенса

• Тангенсом угла х называется отношение синуса
угла х к косинусу угла х.
sin
tg
cos
x
(1;0)
tg x

8. Определение котангенса

• Котангенсом угла х называется отношение косинуса
угла х к синусу угла х.
cos
сtg
sin

9. Тригонометрическая окружность

10.

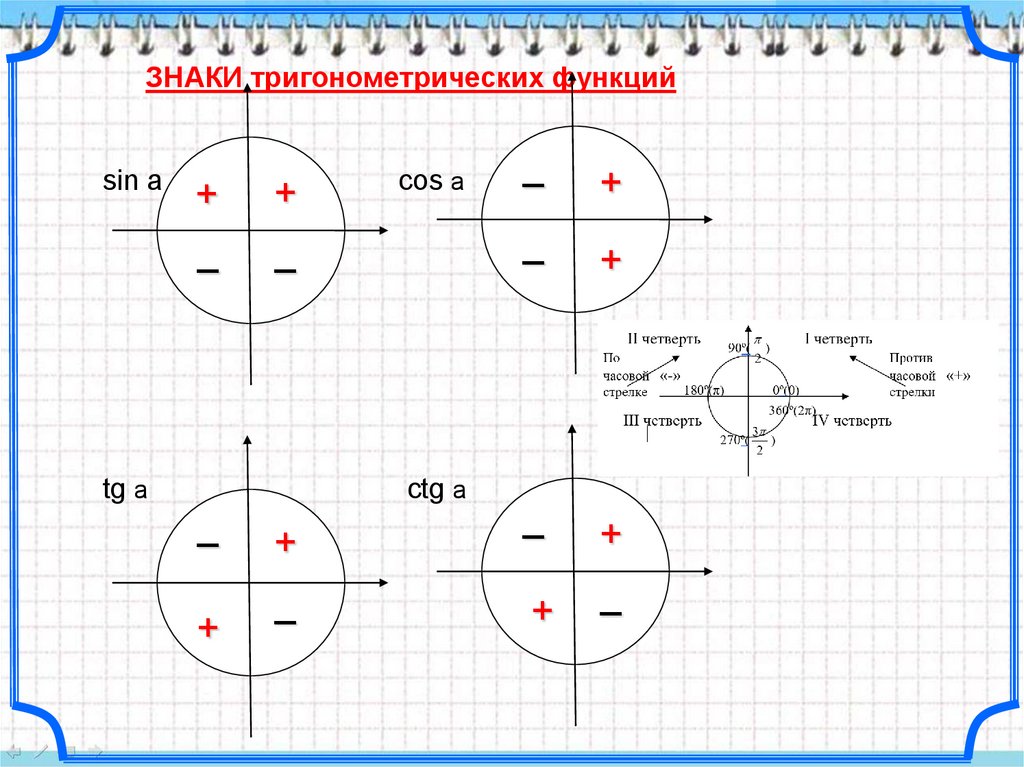
ЗНАКИ тригонометрических функций
sin a
+
+
–
–
tg a
cos a
–
+
–
+
ctg a
–
+
–
+
+
–
+
–

11.

12.

ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ
ЗНАЧЕНИЙ СИНУСА, КОСИНУСА,
ТАНГЕНСА И КОТАНГЕНСА
sin α
cos α
Область
опреде- (- ∞;+ ∞) (- ∞;+ ∞)
ления
Область
значений
1;1 1;1
tg α
2
+
ctg α
n n
n-целое число
(- ∞;+ ∞)
n-целое число
(- ∞;+ ∞)

13.

ТАБЛИЦА ЗНАЧЕНИЙ
ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
α
0° 30° 45° 60° 90° 180° 270° 360°
0
6
4
3
π
3
2
sin α 0
1
2
2
2
2
3
2
1
0
-1
0
cos α 1
3
2
2
2
1
2
0
-1
0
1
3
3
1
3
-
0
-
0
0
-
0
-
tg α 0
ctg α -
3
1
3
3
2π

14. Пример: Вычислить

3
3 2 3
1
3
3
3sin +2cos -tg =3∙ +2∙ - 3 =
- 3= + 3- 3=
2
2
2
2
2
2
6
6
3
Задание:Вычислить

15. Учебник «Алгебра и начала анализа» (10 кл.)

Стр.178 № 563(2,3,4)
Стр.179 № 567
Стр.179 № 566