Similar presentations:
Аналитическая механика
1.
Московский государственный университет путей сообщения (МИИТ)Кафедра теоретической механики
Научно-технический центр транспортных технологий
Бондаренко А.Н.
Курс лекций по
теоретической
механике
Динамика (II часть)
Электронный учебный курс написан на основе лекций, читавшихся автором для студентов, обучавшихся
по специальностям СЖД, ПГС и СДМ в НИИЖТе и МИИТе (1974-2006 гг.). Учебный материал
соответствует календарным планам в объеме трех семестров.
Для полной реализации анимационных эффектов при презентации необходимо использовать средство просмотра Power Point
не ниже, чем встроенный в Microsoft Office операционной системы Windows-ХР Professional.
Запуск презентации – F5, навигация – Enter, навигационные клавиши, щелчок мыши, кнопки.
Завершение – Esc.
Замечания и предложения можно послать по e-mail: bond@miit.ru .
Москва - 2007
2.
СодержаниеЛекция 7. Аналитическая механика. Обобщенные координаты. Уравнения связей. Возможные перемещения.
Идеальные связи. Принцип возможных перемещений. Примеры использования принципа возможных
перемещений при определении реакций связей.
Общее уравнение динамики. Пример решения задачи на применение общего уравнения динамики. Обобщенные
силы. Уравнение Лагранжа II рода.
Рекомендуемая литература
1. Яблонский А.А. Курс теоретической механики. Ч.2. М.: Высшая школа. 1977 г. 368 с.
2. Мещерский И.В. Сборник задач по теоретической механике. М.: Наука. 1986 г. 416 с.
3. Сборник заданий для курсовых работ /Под ред. А.А. Яблонского. М.:Высшая школа. 1985 г. 366 с.
4. Бондаренко А.Н. “Теоретическая механика в примерах и задачах. Динамика” (электронное пособие
www.miit.ru/institut/ipss/faculties/trm/main.htm ), 2004 г.
3.
Лекция 7■
Аналитическая механика – устанавливает общие, единые методы изучения движения и равновесия любых самых сложных материальных систем
средствами математического анализа. Для этого вводятся новые понятия и обобщаются старые.
■
Связи – рассматриваются теперь как некоторые условия, налагаемые на систему, которые должны удовлетворяться в процессе движения системы. Они
содержат соотношения (уравнения или неравенства) между координатами, компонентами скоростей и ускорений и, возможно, времени.
Классификация связей: По интегрируемости:
Голономные (геометрические) – выражаются конечными уравнениями относительно координат или интегрируемыми дифференциальными уравнениями
относительно координат:
( x , y , z , t ) 0
k
k
k
Неголономные (кинематические) - выражаются неинтегрируемыми дифференциальными уравнениями относительно координат,
т.е. уравнениями, содержащими не только координаты точек системы, но и их производные по времени:
( xk , yk , zk , x k , y k , z k , t ) 0
Неинтегрируемость состоит в том, что их нельзя привести к виду уравнений голономной связи.
По зависимости от времени:
Склерономные (стационарные) – не зависящие от времени:
( xk , yk , z k ) 0
Например, уравнение траектории, полученное для некоторой точки шатуна кривошипно-шатунного механизма:
рассматривается как уравнение cклерономной голономной связи:
x2 y2
a2
b2
1
Реономные (нестационарные) – зависящие от времени. Например, кинематическое возбуждение колебаний.
По освобождаемости:
Неосвобождающие (удерживающие или двухсторонние) – описываются уравнением, исключающим возможность покидания точкой траектории
или поверхности, описываемой уравнением. Этому соответствует, например, жесткая связь в виде шарнирного стержня.
Освобождающие (неудерживающие или односторонние) – выражаются неравенством, регламентирующим связь лишь в одном направлении, например, гибкая
нить или гладкая поверхность.
■
■
Обобщенные координаты – независимые параметры, однозначно определяющее положение механической системы при ее движении. Обобщенность состоит в том, что
они могут иметь различную природу (линейные или угловые перемещения относительно некоторого начального положения или какие-либо другие величины). Общее
обозначение – qi (i = 1,…,n).
Число степеней свободы – число независимых обобщенных координат, через которые можно выразить декартовые координаты всех точек системы. Например:
y
x A l cos ;
xA
A
l
O
yA
y A l sin
x
Здесь положение любой точки стержня (например, А) однозначно определяется
значением всего одной величины – угла , который является обобщенной координатой (q
= ). Число степеней свободы равно n = 1.
Уравнение связи для рассматриваемой точки A:
x 2 y 2 l 2
1
4.
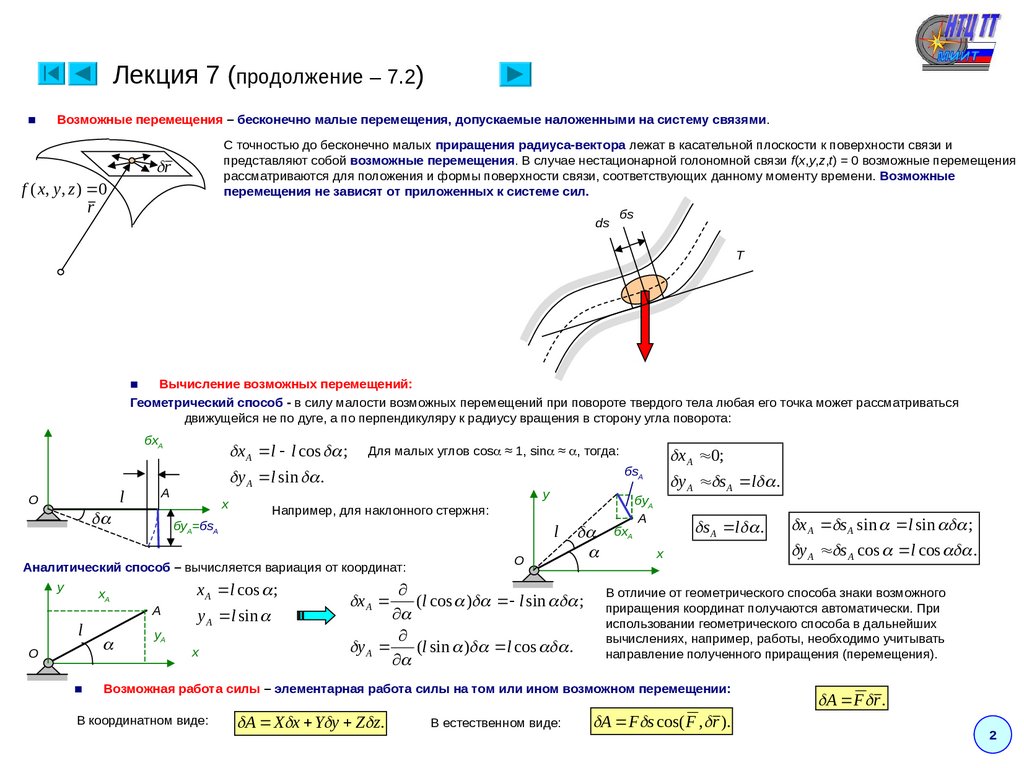
Лекция 7 (продолжение – 7.2)■
Возможные перемещения – бесконечно малые перемещения, допускаемые наложенными на систему связями.
С точностью до бесконечно малых приращения радиуса-вектора лежат в касательной плоскости к поверхности связи и
представляют собой возможные перемещения. В случае нестационарной голономной связи f(x,y,z,t) = 0 возможные перемещения
рассматриваются для положения и формы поверхности связи, соответствующих данному моменту времени. Возможные
перемещения не зависят от приложенных к системе сил.
r
f ( x, y , z ) 0
r
бs
ds
T
■
Вычисление возможных перемещений:
Геометрический способ - в силу малости возможных перемещений при повороте твердого тела любая его точка может рассматриваться
движущейся не по дуге, а по перпендикуляру к радиусу вращения в сторону угла поворота:
бxA
A
l
O
x A l l cos ;
y A l sin .
x
Для малых углов cos ≈ 1, sin ≈ , тогда:
y
Например, для наклонного стержня:
бyA=бsA
l
Аналитический способ – вычисляется вариация от координат:
y
x A l cos ;
xA
A
l
O
■
yA
y A l sin
x
x A 0;
y A s A l .
бsA
O
(l cos ) l sin ;
y A (l sin ) l cos .
x A
бxA
бyA
A
s A l .
x
В отличие от геометрического способа знаки возможного
приращения координат получаются автоматически. При
использовании геометрического способа в дальнейших
вычислениях, например, работы, необходимо учитывать
направление полученного приращения (перемещения).
Возможная работа силы – элементарная работа силы на том или ином возможном перемещении:
В координатном виде:
A X x Y y Z z.
В естественном виде:
x A s A sin l sin ;
y A s A cos l cos .
A F s cos( F , r ).
A F r .
2
5.
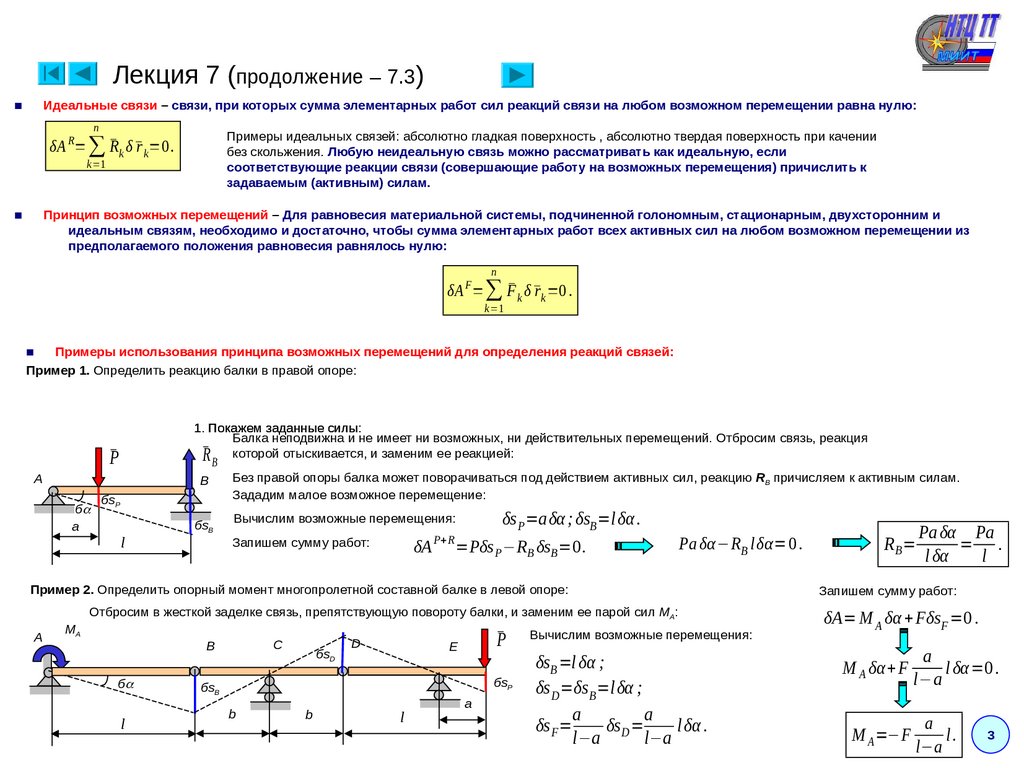
Лекция 7 (продолжение – 7.3)■
Идеальные связи – связи, при которых сумма элементарных работ сил реакций связи на любом возможном перемещении равна нулю:
n
Примеры идеальных связей: абсолютно гладкая поверхность , абсолютно твердая поверхность при качении
без скольжения. Любую неидеальную связь можно рассматривать как идеальную, если
соответствующие реакции связи (совершающие работу на возможных перемещения) причислить к
задаваемым (активным) силам.
R
δA = ∑ R̄k δ r̄ k=0.
k =1
■
Принцип возможных перемещений – Для равновесия материальной системы, подчиненной голономным, стационарным, двухсторонним и
идеальным связям, необходимо и достаточно, чтобы сумма элементарных работ всех активных сил на любом возможном перемещении из
предполагаемого положения равновесия равнялось нулю:
n
F
δA = ∑ F̄ k δ r̄ k =0 .
k =1
■
Примеры использования принципа возможных перемещений для определения реакций связей:
Пример 1. Определить реакцию балки в правой опоре:
1. Покажем заданные силы:
Балка неподвижна и не имеет ни возможных, ни действительных перемещений. Отбросим связь, реакция
R̄ B которой отыскивается, и заменим ее реакцией:
Без правой опоры балка может поворачиваться под действием активных сил, реакцию RB причисляем к активным силам.
B
Зададим малое возможное перемещение:
P̄
A
б
a
бsP
l
бsB
δs P=a δα ; δsB =l δα .
Вычислим возможные перемещения:
Запишем сумму работ:
δA
P+R
=Pδs P −RB δsB =0.
Pa δα−RB lδα=0 .
Пример 2. Определить опорный момент многопролетной составной балке в левой опоре:
Отбросим в жесткой заделке связь, препятствующую повороту балки, и заменим ее парой сил MA:
A
MA
C
B
б
l
бsD
D
P̄
E
бsP
бsB
b
b
l
a
Вычислим возможные перемещения:
δsB =l δα ;
δs D=δs B=lδα ;
a
a
δs F=
δsD =
l δα .
l−a
l−a
R B=
Pa δα Pa
= .
l δα
l
Запишем сумму работ:
δA= M A δα + Fδs F =0 .
M A δα+ F
M A =−F
a
l δα=0 .
l−a
a
l.
l−a
3
6.
Лекция 7(продолжение-7.4)
■
Общее уравнение динамики – Принцип возможных перемещений, дающий общий метод решения задач статики, можно применить к решению задач
динамики, а именно:
1. Применить принцип Даламбера, сводящий задачу динамики с задаче статики:
2. Применить принцип возможных перемещений, решающий эту статическую задачу:
Общее уравнение динамики:
В любой момент времени сумма работ всех задаваемых сил и сил инерции несвободной механической
системы сидеальными связями на любом возможном перемещении равна нулю.
( Pk k ) rk 0
( Pk mk a k ) rk 0.
A 0,где бA – возможная работа всех задаваемых сил и сил инерции на любом возможном перемещении.
Или еще короче:
Пример. Центробежный регулятор вращается вокруг вертикальной оси с постоянной скоростью. При = 0 пружина не деформирована. Жесткость пружины c.
Длина каждого из стержней l. Плечо подвески a. Вес каждого из шаров G, вес муфты G1. Определить угловую скорость установившегося вращения для
данного угла .
1. Покажем заданные силы:
x
a ос
a
R l
a ос
R
G
G1
B
y
A
ma ос ;
G
ma ос 2 (a l sin ).
g
3. Упругая связь (пружина), не являющаяся идеальной (совершает работу на возможных перемещениях), должна быть
отброшена и заменена реакцией, которая включается в число заданных сил:
G
l
2. Добавим силы инерции:
Модуль реакции пружины пропорционален изменению
длины (укорочению) пружины:
4. Определим проекции возможных перемещений
(вариации координат) точек приложения сил:
5. Составим общее уравнение динамики:
A 2G y A (G1 R ) y B 2 x A 0
Подставим значения сил инерции
и реакции пружины:
Отсюда после некоторых сокращений
и упрощений:
R c l c(2l 2l cos ) 2cl (1 cos ).
x A l cos ;
x A a l sin ;
y A l sin ;
y A l cos ;
y B 2l cos .
2G ( l sin ) (G1 2cl (1 cos ))( 2l sin ) 2
(G G1 2cl (1 cos )) g tg
G (a l sin )
y B 2l sin .
G 2
(a l sin )l cos 0
g
4
7.
Лекция 7 (продолжение – 7.5)■
.
Обобщенные силы
N
Qj
Fk s kj cos( Fk , s kj ) A
qj
k 1
q j
q j
.
-обобщенная сила Qj, соответствующая обобщенной координате qj– скалярная
величина, равная отношению элементарной работы заданных сил на всех
перемещениях системы, вызванных элементарным приращением бqj ≠ 0
координаты qj, к величине этого приращения.
1. Размерность этой силы определяется размерностью обобщенной координаты. Например, если qj есть линейная обобщенная координата, то размерность
обобщенной силы Qj соответствует силе (Н). Если qj есть угловая обобщенная координата, то размерность обобщенной силы Qj соответствует паре сил или
моменту (Нм).
2. Число обобщенных сил равно числу обобщенных координат. Размерность каждой из обобщенных сил определяется размерностью соответствующей
обобщенной координаты.
■
Уравнение Лагранжа II рода – Уравнения представляют собой дифференциальные уравнения движения системы относительно обобщенных координат
системы. Воспользуемся общим уравнением динамики:
d T T
Q j ( j 1,2,..., s).
dt q j q j
5





 physics
physics








