Similar presentations:
Математические модели процессов тепломассообмена
1. Математические модели процессов тепломассообмена
Теплопроводность:● Дифференциальное уравнение
теплопроводности
● Условия однозначности
2. Дифференциальное уравнение теплопроводности
dQz dzz
dQx
dz
dQy dy
dQy
0
x
dQx dx dy
dQz
dx
y
3. Метод математической физики
Для вывода дифференциального уравнениятеплопроводности используется
метод математической физики,
когда процесс изучается в элементарном объеме
d
dv за бесконечно малый промежуток времени
,
что позволяет упростить вывод.
Принимаются допущения:
● тело – однородно и изотропно, то есть его
физические свойства изменяются одинаково
во всех направлениях;
● физические свойства тела постоянны;
4. Допущения
● изменение объема тела от температурыпренебрежимо мало, по сравнению с его объемом,
как величина 2 порядка малости;
● распределение внутренних источников теплоты
равномерно и может быть задано как
qv f ( x, y, z, .)
Тогда по закону сохранения энергии
уравнение теплового баланса запишется в виде:
dQ dQ1 dQ2
,
(1)
где изменение внутренней энергии элементарного объема
d
dv за бесконечно малый промежуток времени
(2)
dQ c t dvd ;
5. Уравнения (3 – 7)
тепловыделения внутренних источников:dQ2 qv dvd
;
(3)
теплота, вошедшая теплопроводностью в элементарный объем
dv за бесконечно малый промежуток времени d вдоль осей
координат x, y, z:
(4)
dQ dQ dQ dQ .
1
x1
y1
z1
Разность подведенной и отведенной теплоты вдоль оси х:
dQx1 dQx dQx dx
,
где:
;
dQ q dydzd
x
(5)
(6)
x
dQx dx qx dx dydzd .
(7)
6. Уравнения (8 - 11)
Функциюqx dx можно разложить в ряд Тейлора:
2
qx dx q x dx 2 ...
qx dx qx
x 1! x 2 2!
.
(8)
Пренебрегаем величиной 2 порядка малости в (8).
После подстановки (8) в (7), а (6) и (7) – в (5) имеем:
dQx1 (qx qx
Аналогично
по осям у и z:
qx
q
q
dx)dydzd x dxdydzd x dvd .
x
x
x
dQy1 dQy dQy dy
q y
dvd
y
q
dQz1 dQz dQz dz z dvd
z
(9)
;
(10)
.
(11)
7. Уравнения (12 – 13)
Уравнения (9), (10), (11) подставляем в (4):qx q y qz
dQ1 (
)dvd
x y z
,
(12)
а уравнения (2), (3), (12) – в (1):
qx q y qz
t
c dvd (
)dvd qv dvd .
x y z
После сокращения на
dvd
и деления на
q
t
1 q q q
( x y z ) v
c x y z
c
По закону Фурье:
qx
c
получим:
t
t
t
; qy ; qz
x
y
z
.
.
(13)
8. Уравнения (14 – 17)
Производные от тепловых потоков по координатам:qx
2t q y
2t qz
2t
2 ;
2 ;
2 .
x
x y
y z
z
(14)
После подстановки (14) в (13) дифференциальное уравнение
теплопроводности будет иметь вид (15):
t 2t 2t 2t qv
( 2 2 2)
.
c x y z
c
(15)
Введя обозначения коэффициента температуропроводности
(16)
a /(c ) и оператора Лапласа 2t 2t 2t 2t
Получим окончательное выражение
x 2 y 2 z 2
дифференциального уравнения
t
2t qv
a
теплопроводности:
(17)
c
9. Полярная (цилиндрическая) система координат
Оператор Лапласа вполярных координатах:
2t
z
2t 1 t 1 2t 2t
2 2 2
2
r r r r z
r
x rCos
y rSin
x2 y 2
arctg( y / x)
z z
z
0
r – радиус – вектор
- полярный угол
r
y
x
y
0
r
y
x
y
x
x
10. Условия однозначности
Дифференциальное уравнение теплопроводности (17)справедливо для ортогональных и полярных координат,
с учетом выражений операторов Лапласа соответственно
(16) и приведенного на предыдущем слайде.
Дифференциальное уравнение теплопроводности (17)
описывает множество процессов теплопроводности.
Чтобы выделить конкретный процесс, надо задать условия
однозначности. Их бывает 4 вида: геометрические (геометрия
тела, его размеры, положение в пространстве);
физические (физические свойства тела); начальные [при 0
t f ( x, y, z)] и граничные условия, которые бывают 4 родов.
11. Граничные условия
I рода: t f ( x, y, z, ) ,для стационарных процессов они принимают вид: t Const .
c
II рода: q f ( x, y, z, ) ,
или для стационарных процессов: qc Const .
III рода (для теплопроводности внутри ламинарного
пограничного слоя и конвекции вне его):
t
, откуда: t
.
q ( )c (tc tж )
n
(
n
)c (tc tж )
IV рода (для теплопроводности при контакте двух твердых
тел):
t1
t2 , откуда: ( t1 ) ( t2 ) .
q ( ) ( )
1
c
2
c
1
n
c
2
n
c
n
n
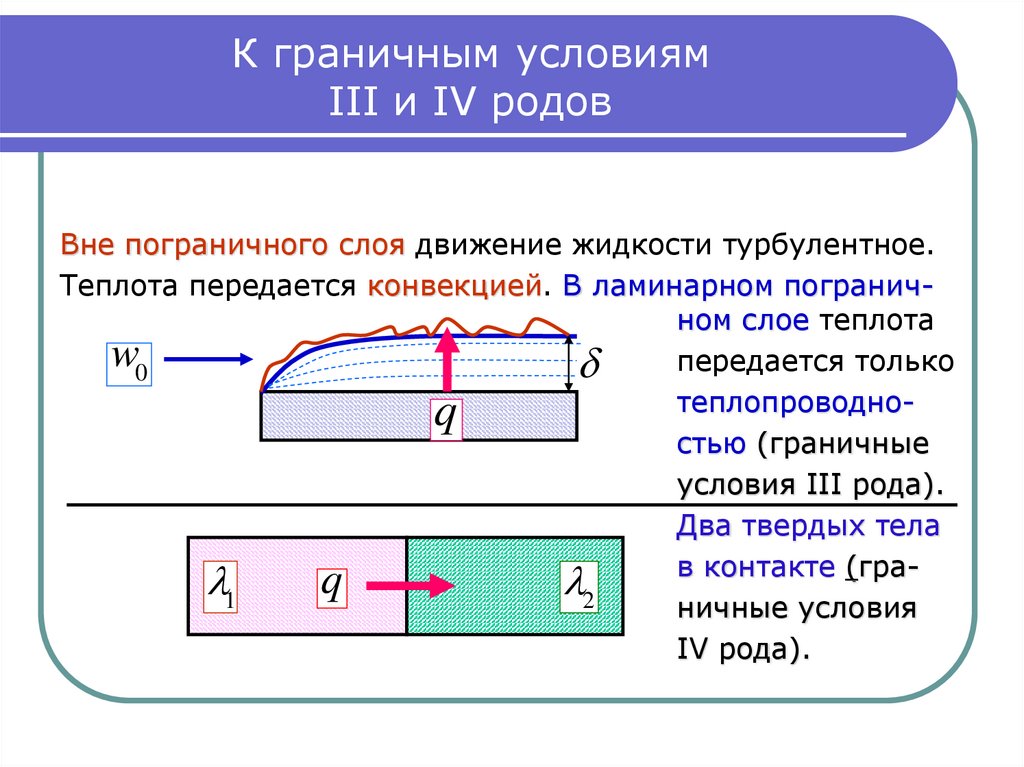
12. К граничным условиям III и IV родов
Вне пограничного слоя движение жидкости турбулентное.Теплота передается конвекцией. В ламинарном пограничном слое теплота
w0
передается только
теплопроводностью (граничные
условия III рода).
Два твердых тела
в контакте (граq
1
2
ничные условия
IV рода).
q











 physics
physics








