Similar presentations:
Вектори у просторі
1.
ВЕКТОРИ УПРОСТОРІ
2. Зміст
1.Поняття вектора.2.Координати вектора.
3.Абсолютна величина вектора.
4.Рівні вектори.
5.Колінеарні вектори.
6.Компланарні вектори.
7.Дії над векторами.
8.Скалярний добуток векторів.
9.Приклади.
3. Вектор
Герман ГрассманГамільтон
Поняття вектора
з'явилося в роботах
німецького математика XIX
ст. Г. Грассмана та
ірландського математика У.
Гамільтона. Згодом воно
було охоче сприйняте
багатьма математиками і
фізиками. В сучасній
математиці це поняття
відіграє дуже важливу роль.
4. Поняття вектора
аа
АВ, АВ, а, а
АА
АА 0
•Вектор - це величина, яка
характеризується
числовим значенням і
напрямком.
•Вектор - напрямлений
відрізок.
•Під направленим
відрізком розуміють
впорядковану пару точок,
перша з яких - точка A називається
його початком, а друга B - його кінцем.
5. Координати вектора
AB( xB xA ; yB y A ; zB z A )OA( x A ; y A ; z A )
•Координати вектора
дорівнюють різниці
координат його кінця та
початку
•Координати вектора, для
якого початком є початок
координат дорівнюють
координатам його кінця
6. Абсолютна величина вектора
AB x2
AB
y
2
AB
z
2
AB
a x y z
2
a
2
a
0 0
2
a
Абсолютна величина
вектора
( модуль вектора,
довжина вектора)
дорівнює кореню
квадратному із
суми квадратів його
координат
7. Напрямленість векторів
•Векториі
називають протилежно
напрямленими, якщо
протилежно напрямлені
півпрямі AB і CD .
•Вектори
і
називають
співнапрямленими,
якщо співнапрямлені
півпрямі AB і CD.
8.
Рівні векториb
d
a
• Рівні вектори – це
вектори, що
мають рівні
a b
абсолютні
a b
величини та
однаковий напрям.
• Рівні вектори – це
a b,
вектори, що
xa xb ,
мають рівні
координати.
y y ,
a
b
z a zb
9. Колінеарні вектори
ВКолінеарні вектори
–
A
а
b
C
D
це вектори, що
лежать
на паралельних
прямих,
або на одній прямій
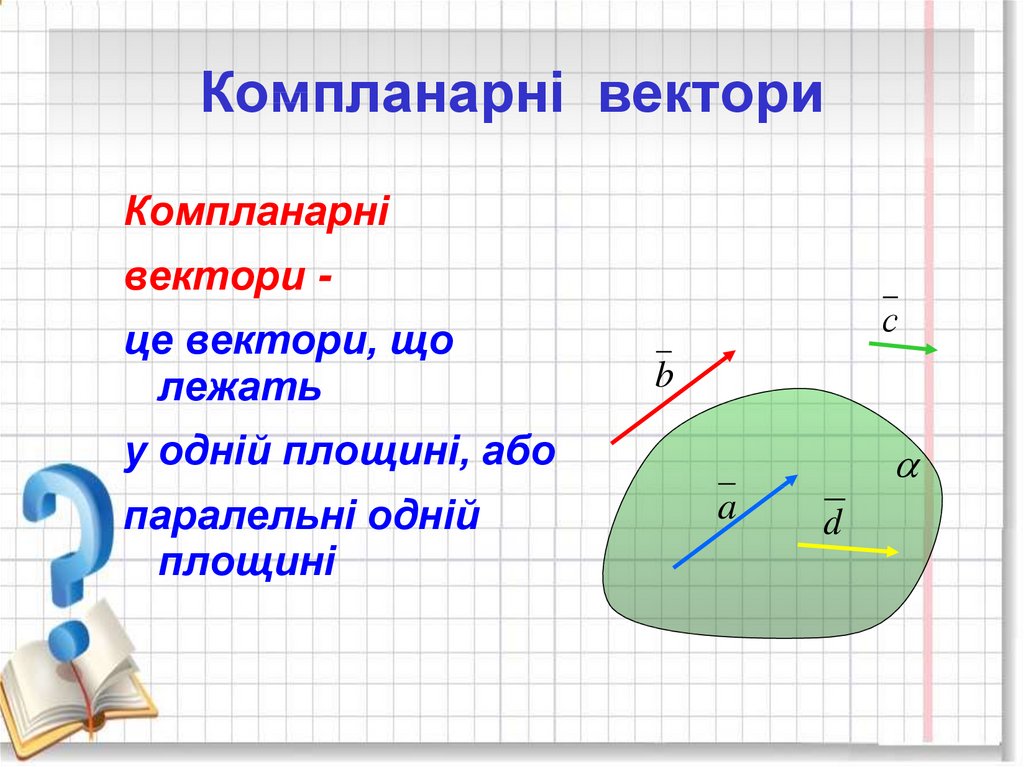
10. Компланарні вектори
Компланарнівектори це вектори, що
лежать
с
b
у одній площині, або
паралельні одній
площині
a
d
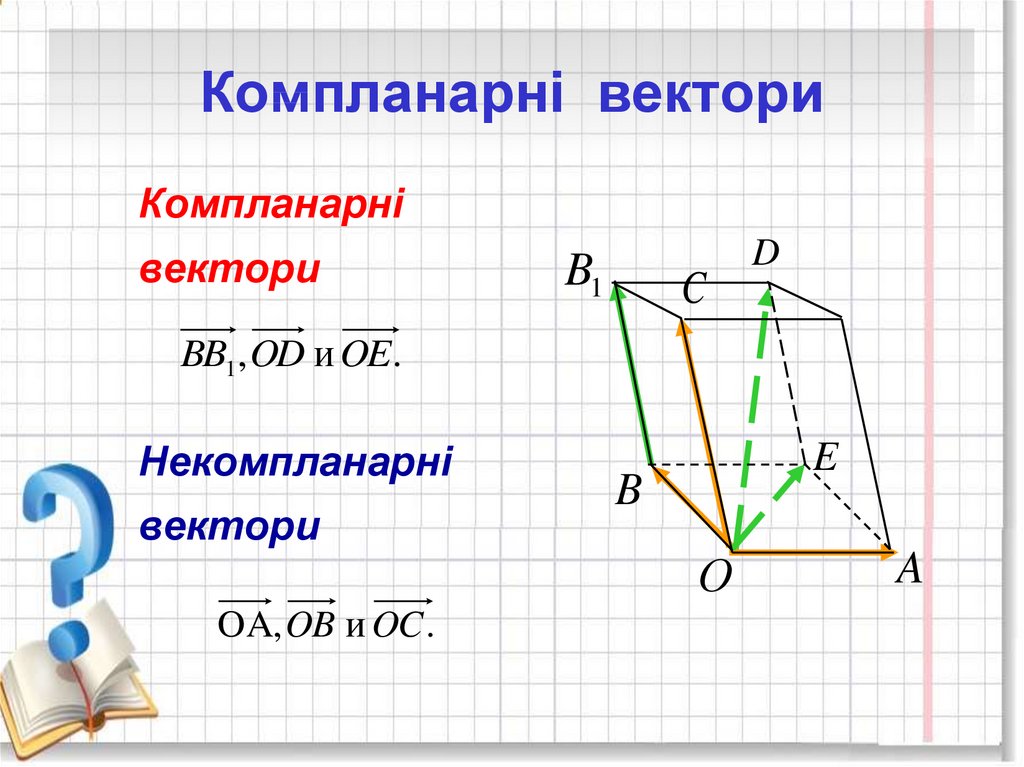
11. Компланарні вектори
Компланарнівектори
B1
C
D
BB1, OD и OE.
Некомпланарні
вектори
E
B
О
OA, OB и OC .
A
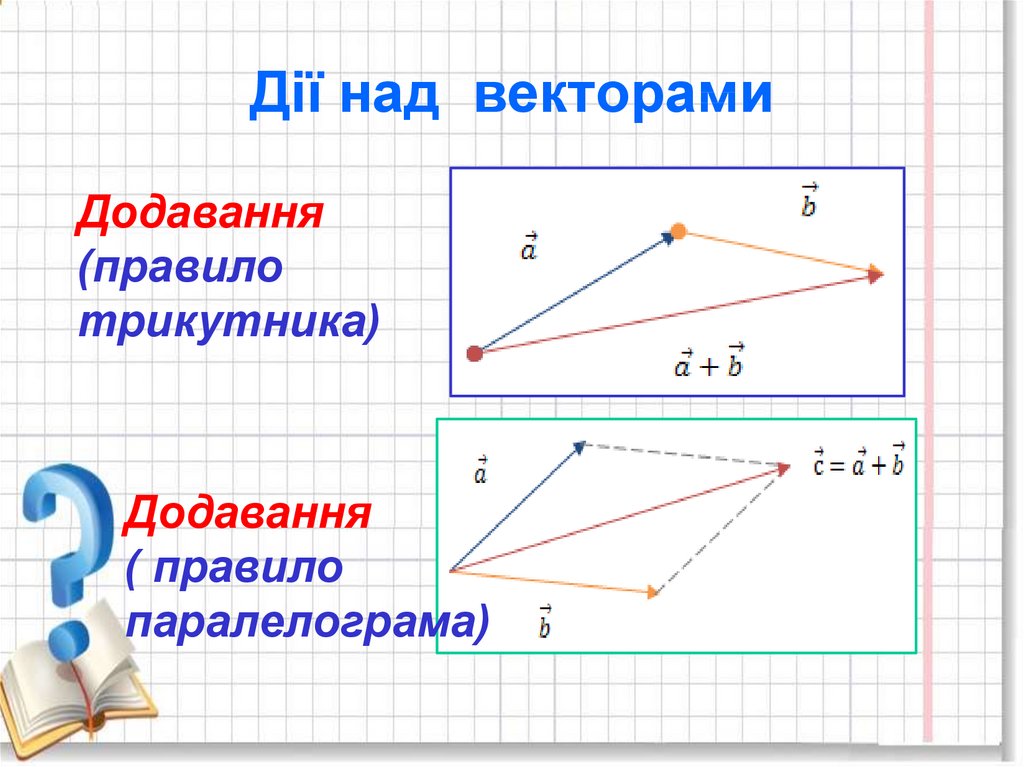
12. Дії над векторами
Додавання(правило
трикутника)
Додавання
( правило
паралелограма)
13. Дії над векторами
Додавання (правилотрикутника)
•За правилом трикутника
обидва вектора
переносяться паралельно
самим собі так, щоб
початок одного з них
збігався з кінцем іншого.
•Вектор суми задається
третьою стороною
трикутника, що утворився,
причому його початок
збігається з початком
першого вектора.
14. Дії над векторами
•За правиломпаралелограма обидва
вектора переносяться
паралельно самим собі
так, щоб їх початки
збігалися.
•Вектор суми задається
діагоналлю побудованого
на них паралелограма, яка
виходить з їх спільного
початку.
Додавання
( правило
паралелограма)
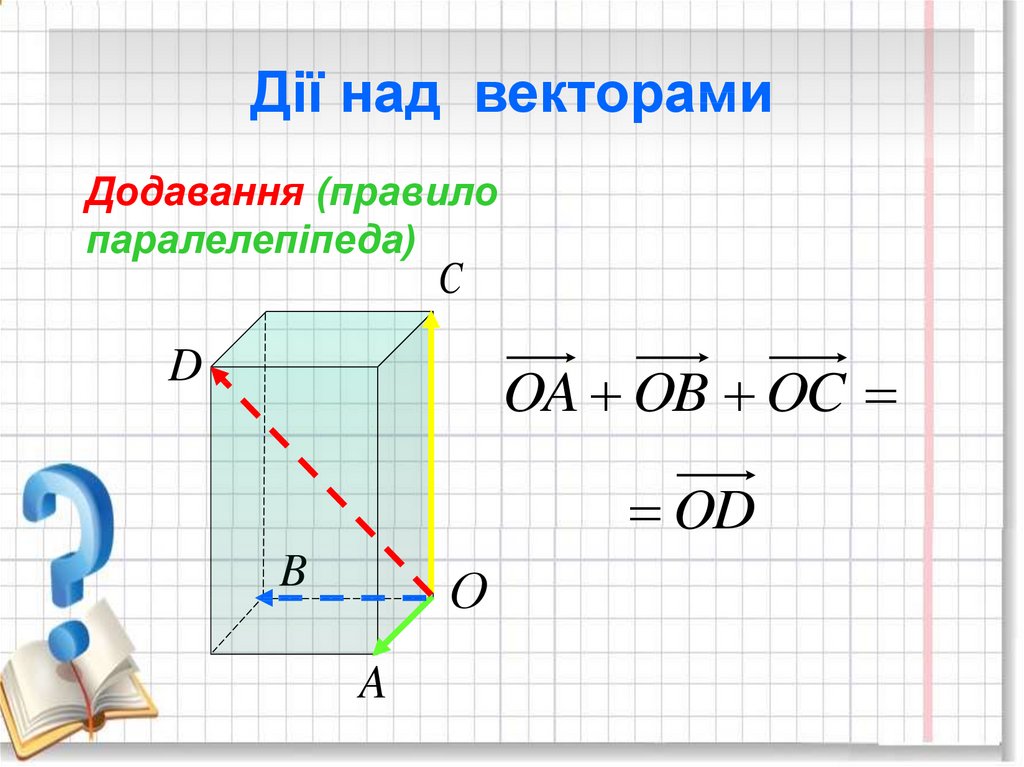
15.
Дії над векторамиДодавання (правило
паралелепіпеда)
C
D
OA OB OC
OD
B
О
A
16. Дії над векторами
Додаванняa xa ; ya ; za b xb ; yb ; zb
xa xb ; ya yb ; za zb
Закони додавання:
1) переставний
2) сполучний
a b b a
( a b) с a ( b c )
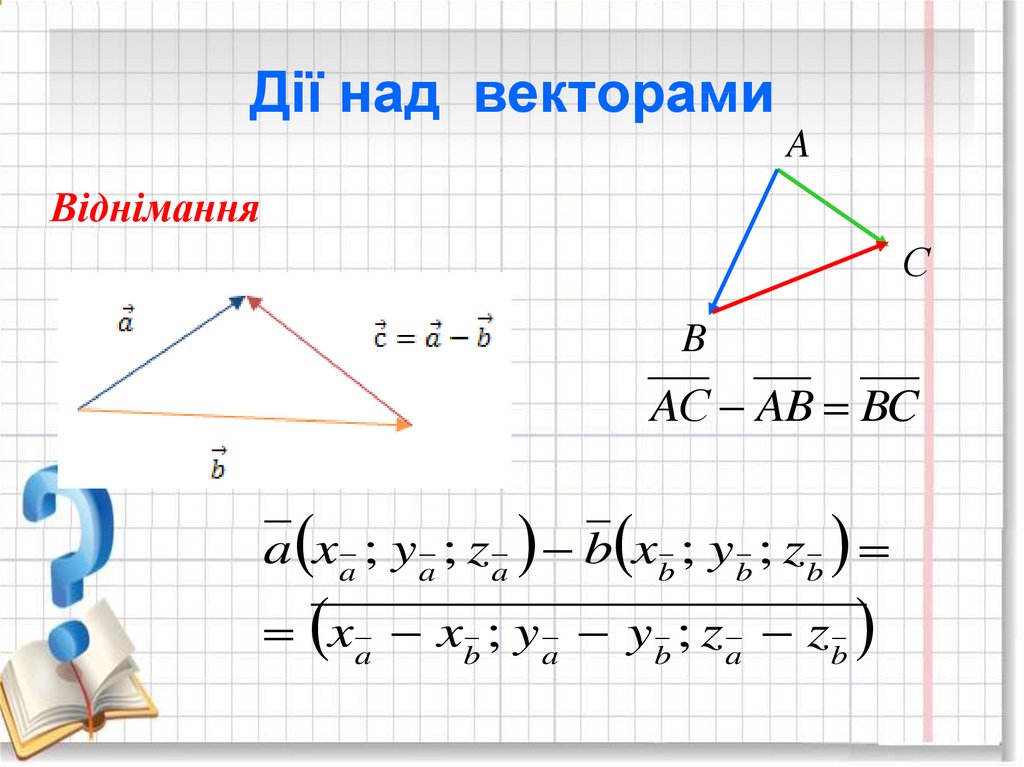
17. Дії над векторами
AВіднімання
С
B
AС AB BC
a xa ; y a ; z a b xb ; y b ; zb
xa xb ; y a y b ; z a zb
18. Дії над векторами
•Множення вектора начисло
a xa ; ya ; za
•Якщо a || b , то
координати векторів
пропорційні.
І навпаки, якщо
координати векторів
пропорційні, то a || b
a
2a
3a
0,5a
xa ya za
a || b
xb yb zb
19. Скалярний добуток векторів
Скалярним добуткомвекторів називається
сума добутків
відповідних координат
Властивості
скалярного добутку
a b a b cos
a b xa xb ya yb za zb
сos
a b
a b
a a
2
2
a b 0, a 0, b 0 a b
20. №1 Знайдіть координати вектора АВ, якщо:
A 3;4;7B 3;2;16
A 2;5;3
B 0;4; 9
A 0;0;0
B 7;8;12
A 3; 4;2
B 3; 6;11
21. №2 Знайдіть абсолютну величину вектора:
a 0;4; 3a 0 4 3 5
b 2; 8;3
b 2 8 3 77
2
2
2
2
B 2; 8;3
A 0;4; 3
AB
2
2
0 2 4 8 3 3
2
184 2 46
2
2
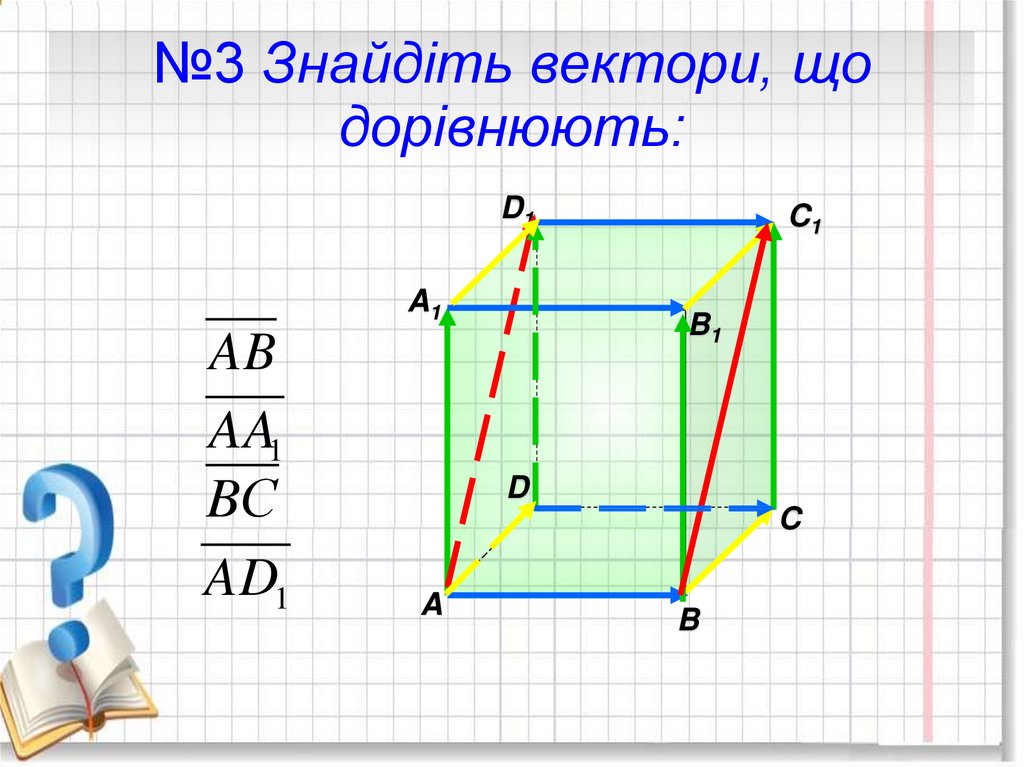
22. №3 Знайдіть вектори, що дорівнюють:
D1A1
AB
AA1
BС
AD1
C1
B1
D
C
A
B
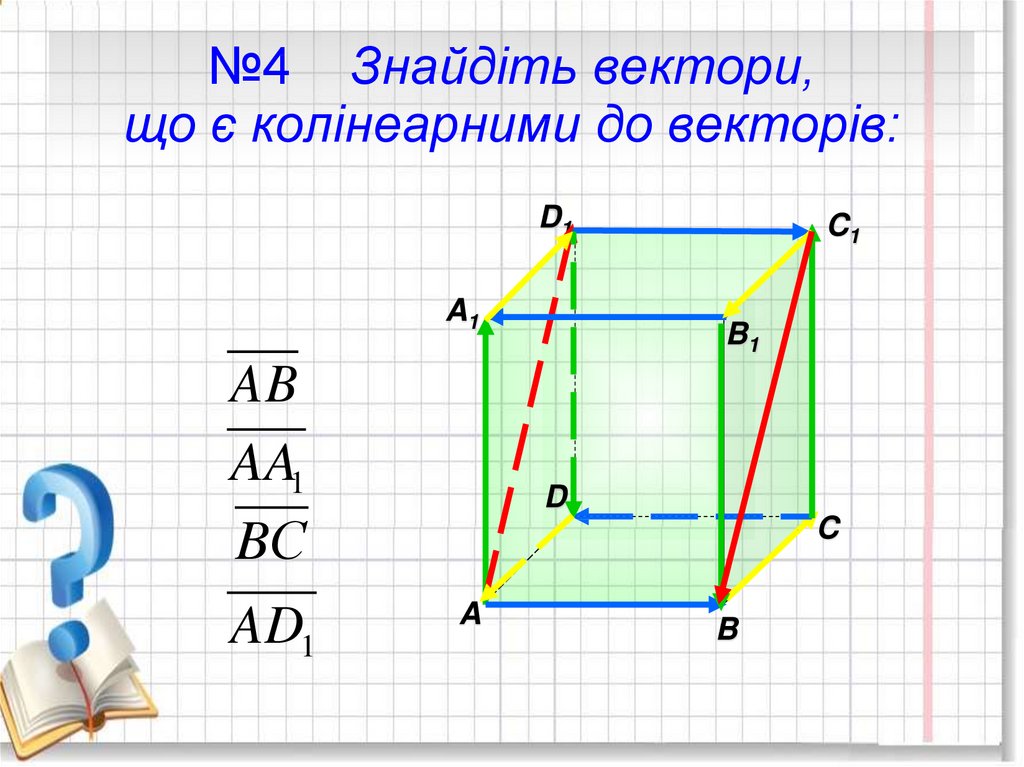
23. №4 Знайдіть вектори, що є колінеарними до векторів:
D1A1
AB
AA1
BС
AD1
C1
B1
D
C
A
B
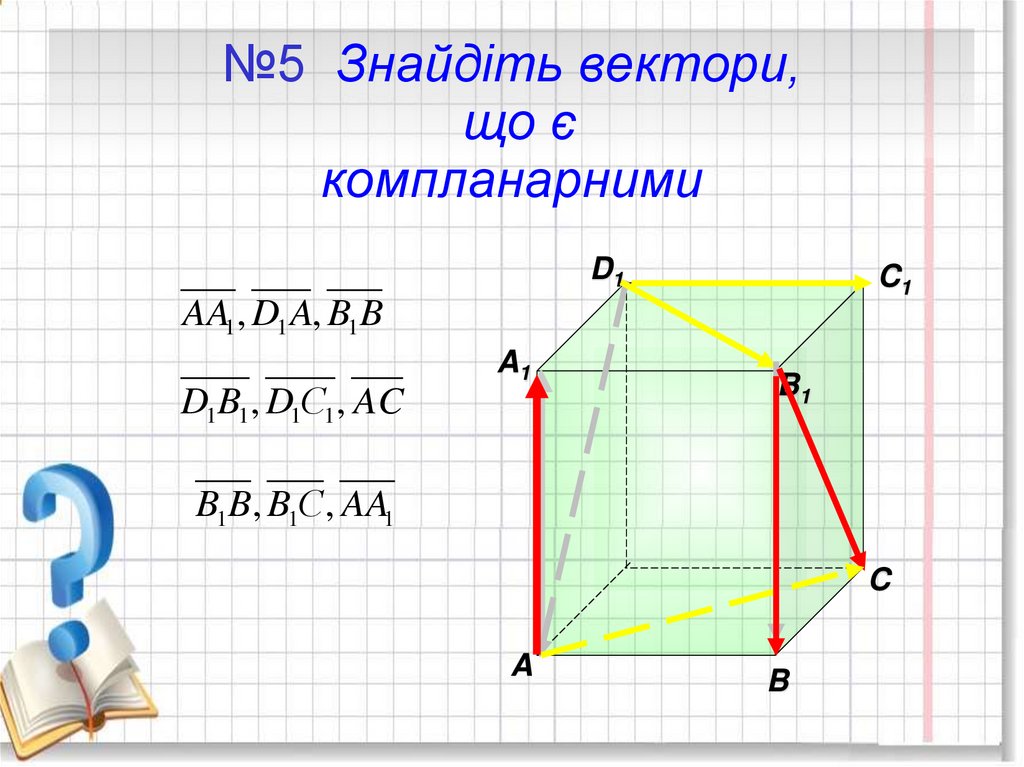
24. №5 Знайдіть вектори, що є компланарними
D1C1
AA1 , D1 A, B1B
D1B1 , D1С1 , AC
A1
B1
B1B, B1С , AA1
C
A
B
25. №6 Спростіть вираз
TR DK HK DF RT FHKT AC AB TK XC BX
№7 Знайдіть вектор
С1
B1
A1
D1
AB C1 B1 BD1
BA D1 A1 CC1
С
B
A
D
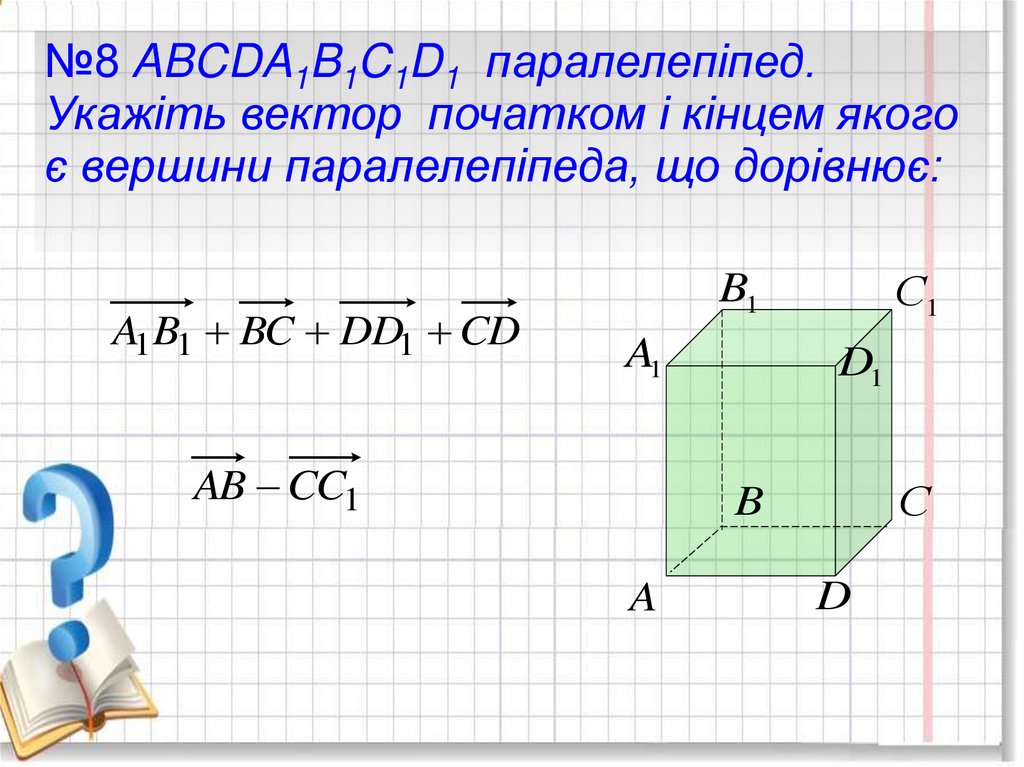
26.
№8 ABCDA1B1C1D1 паралелепіпед.Укажіть вектор початком і кінцем якого
є вершини паралелепіпеда, що дорівнює:
A1B1 BC DD1 CD
С1
B1
A1
AB CC1
D1
С
B
A
D
27. №9 Дано вектори , .
№9 Дано вектори a 2; 5; 4,b 4;3; 3 .
1. Чи будуть колінеарними
?
d a 2b
2.Обчисліть
вектори c 2a 4b та
.
2c 3d
3. Знайдіть координати вектора
1
p 2a b c .
3
4. Знайдіть значення т і п, при яких вектори
6; n;1
і
m;16; 2
будуть колінеарними.
28.
№10 Знайдіть скалярний добутокa b ,
якщо
a 3, b 4, a ; b 120 .
№11
При якому значенні n вектори
2n; 3; 6 і 3; n; 3 будуть
перпендикулярними?
№12 Знайдіть кут між векторами
5; 2;7 і 7;5;2
.
29. Джерела
http://formula.co.ua/vectors.phphttp://uk.wikipedia.org
http://shkolnik.in.ua
Г.П.Бевз,В.Г.Бевз,Н.Г.Владімірова, В.М.Владіміров
Геометрія 11
Підручник для загальноосвітніх навчальних закладів
Академічний рівень, профільний рівень
Рекомендовано Міністерством освіти і науки України
Київ “Генеза” 2011




















 mathematics
mathematics








