Вектори у просторі

1.

2.

План
1. Координати вектора у просторі.
2. Дії над векторами.
3. Скалярний добуток векторів

3.

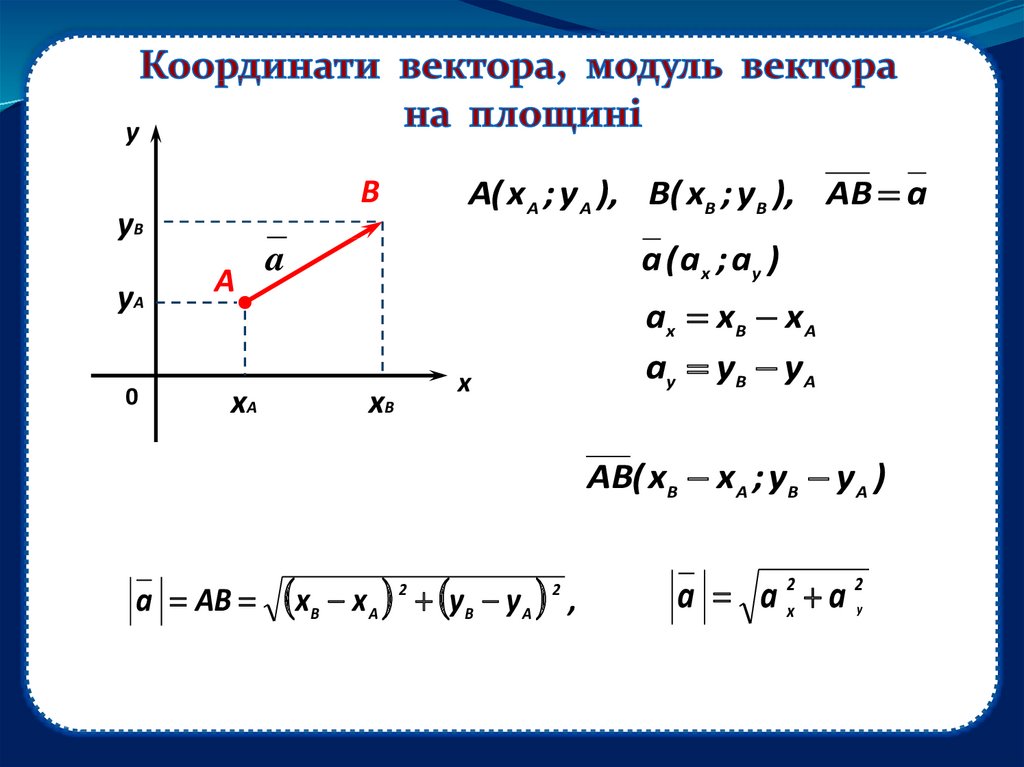
у
уВ
уА
0
A( x A ; y A ), B( xB ; yB ), AB a
В
А
a ( a x ; ay )
a
хА
ax xB x A
ay yB y A
х
хВ
AB( xB x A ; yB y A )
a AB
x
x A yB y A ,
2
B
2
a a 2x a 2
y

4.

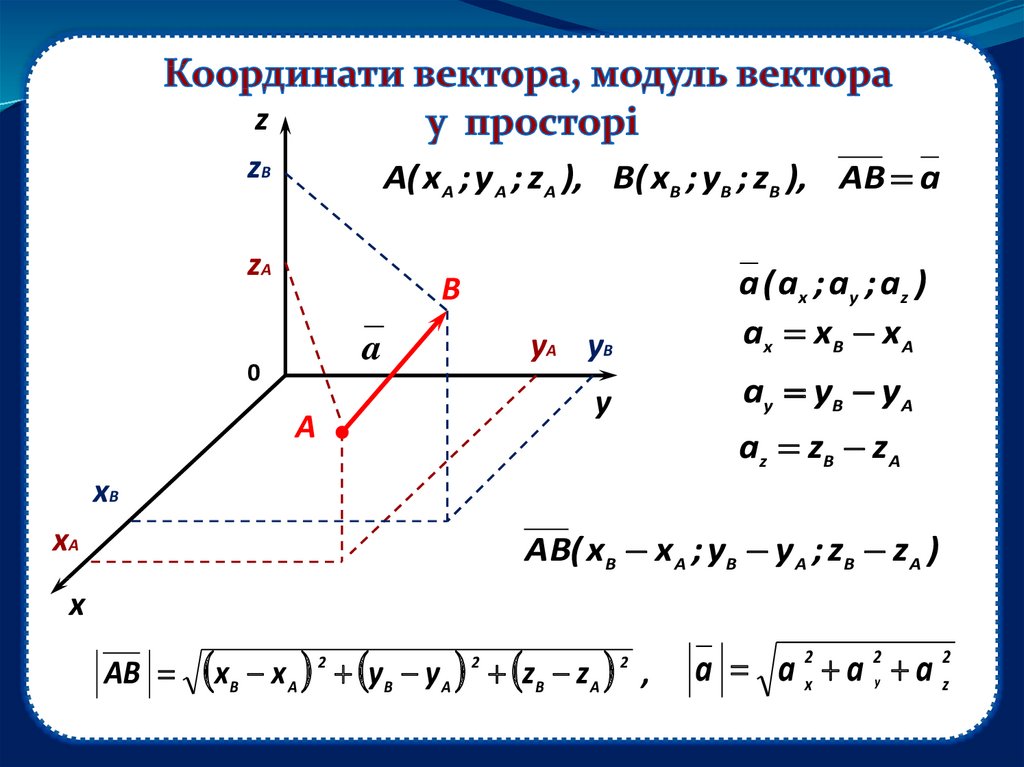
z
zВ
A( x A ; y A ; zA ), B( xB ; yB ; zB ), AB a
zА
В
a
0
А
уА у В
у
a ( a x ; ay ; a z )
ax xB x A
ay yB y A
a z zB z A
хВ
хА
AB( xB x A ; yB y A ; zB z A )
х
AB
x
2
2
2
x
y
y
z
z
,
B
A
B
A
B
A
a a 2x a 2 a 2z
y

5.

a
b
a b
a b
a b
у координатах
ax bx
a ax ; ay ; az b bx ; by ; bz ay by
a b
z
z

6.

№ 1. Знайти координати вектора MF , якщо М(-5; -9; 4) і
F(-2; 1; -3).
Відповідь:
MF( 3 ;10 ; 7 ).
№ 2. Дано точки М(-3; 2; z), N(4; -6; 3), К(х; 1; -10), Е(2; у; -15).
Знайти х, у, z, якщо MN EK .
Відповідь: х = 9, у = 9, z = -2.
№ 3. Серед векторів a( 5 ; 3 ; 4 ), b( 2 ;1; 7 ), c ( 3 ;6 ; 3 ),
m( 5 ; 5 ; 2 ) , n( 2 ; 6 ; 10 ) знайти такі, що мають
однаковий модуль.
Відповідь: a n 50 ,
b c m
54 .

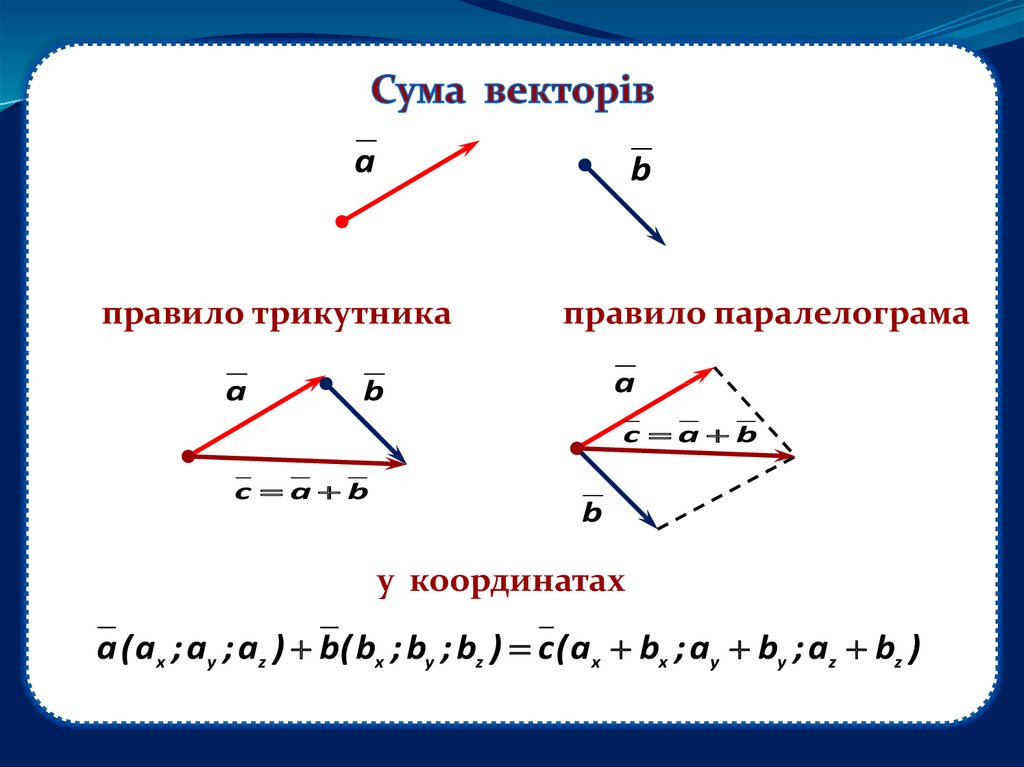
7.

a
b
правило трикутника
a
правило паралелограма
a
b
c a b
c a b
b
у координатах
a ( ax ; ay ; az ) b( bx ; by ; bz ) c ( ax bx ; ay by ; az bz )

8.

a
b
c
М
OB a b
BM c
c
В
a
О
b
OM OB BM
OM a b c

9.

a
b
a
c a b
b
у координатах
a ( ax ; ay ; az ) b( bx ; by ; bz ) c ( ax bx ; ay by ; az bz )

10.

№ 4. Дано вектори
Знайти:
a( 3 ;1; 2 ) і b( 5 ; 6 ;7 ) .
1) а b ;
3) a b ;
2) а b ;
4) a b .
Відповідь: 1) ( 2 ; 5 ; 9 ) ;
2 ) ( 8 ;7 ; 5 ) ;
3 ) 110 ;
4 ) 138 .

11.

a
2a
a ( a x ; ay ; a z )
λ a ( λax ; λay ; λaz )
2a
якщо 0, то а а
якщо 0, то а а

12.

№ 5. Побудувати вектори
2a ; 1,5 a ; 0 ,5a .
a
2a
1 ,5 a
0 ,5 a

13.

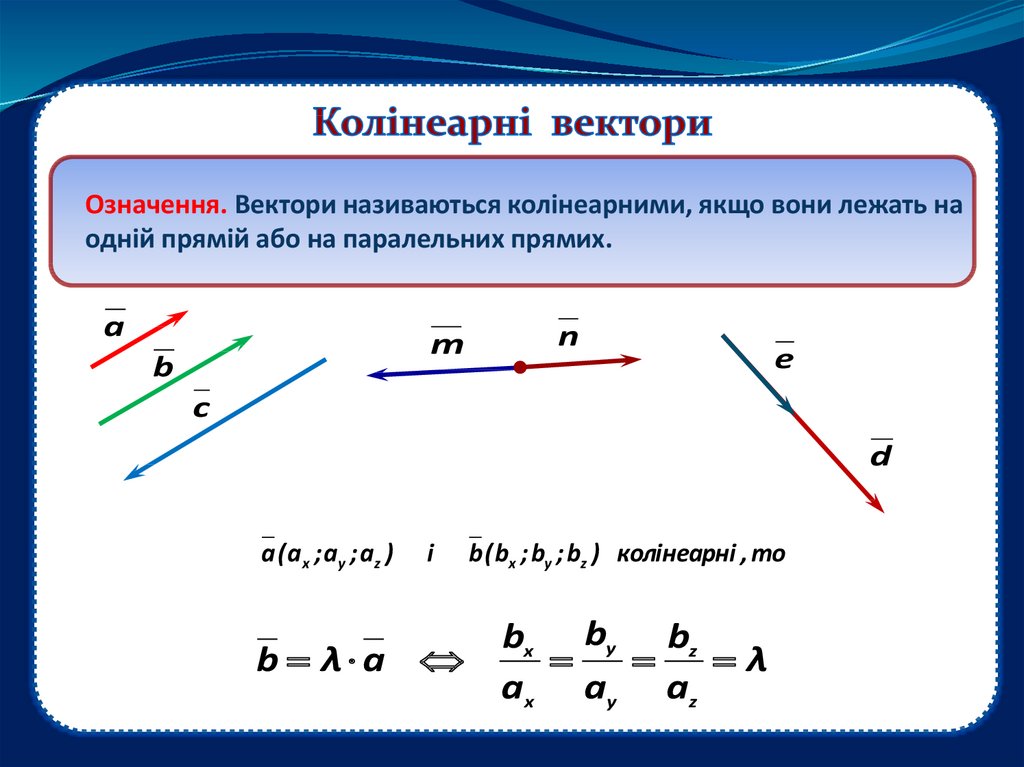
Означення. Вектори називаються колінеарними, якщо вони лежать на
одній прямій або на паралельних прямих.
a
m
b
n
e
c
d
a ( a x ; ay ; a z )
і
b λ a
b ( bx ; by ; bz ) колінеарні , то
bx by bz
λ
a x ay a z

14.

a
a b a b cos
b
у координатах
a ( ax ; ay ; az ), b ( bx ; by ; bz )
a b ax bx ay by az bz
умова перпендикулярності векторів
a b a b 0
a
b

15.

Розв’язування задач
№ 1. Модуль вектора a( x ; 10 ;8 ) дорівнює 13. Знайти х.
№ 2. Дано вектори a( 4 ; 7 ; 3 ) і
1) c 3 b 2 a ;
b( 3 ;6 ; 2 ). Знайти:
2) c .
№ 3. Чи колінеарні вектори AB і CD , якщо А(2; -5; 4),
В(1; 4; 6), С(-4; -6; 8), D(-2; 0; 12) ?
№ 4. Знайти значення х і у, при яких вектори a( x ; 8 ;12 )
і b( 24; y ; 36 ) колінеарні.
№ 5. Знайти скалярний добуток векторів a і
a( 1; 3 ; 8 ), b( 4 ; 2 ; 6 ).
b, якщо

16.

№ 6. Знайти скалярний добуток векторів a
a 8,
і b , якщо
b 7 , ( a , b ) 45 0 .
№ 7. Дано вектори a( 4 ; 2 ; p ) і b( 5 ; p ; 3 ). При якому
значенні р
a b 8?
№ 8. Дано вектори a( 4 ; 7 ; 2 ) і b( 3 ; ó ; 1) . При якому
значенні у вектори перпендикулярні.
№ 9. Довести, що чотирикутник АВСD з вершинами
А(6; -4; 2), В(3; 2; 3), С(0; 1; 0), D(3; -5; -1) - прямокутник.
№ 10. Знайти косинус кута між векторами a( 5 ; 1; 2 ) і
b( 2 ;6 ; 3 ).