Similar presentations:
Вектори у просторі
1.
ВЕКТОРИ УПРОСТОРІ
2. Зміст
1.Поняття вектора.2.Координати вектора.
3.Абсолютна величина вектора.
4.Рівні вектори.
5.Колінеарні вектори.
6.Компланарні вектори.
7.Дії над векторами.
8.Скалярний добуток векторів.
9.Приклади.
3. Поняття вектора
аа
АВ, АВ, а, а
АА
АА 0
•Вектор - це величина, яка
характеризується
числовим значенням і
напрямком.
•Вектор - напрямлений
відрізок.
•Під направленим
відрізком розуміють
впорядковану пару точок,
перша з яких - точка A називається
його початком, а друга B - його кінцем.
4. Координати вектора
AB( xB x A ; y B y A ; z B z A )•Координати вектораOA( x A ; y A ; z A )
дорівнюють різниці
координат його кінця та
початку
•Координати вектора, для
якого початком є початок
координат дорівнюють
координатам його кінця
5. Абсолютна величина вектора
AB x2
AB
y
2
AB
z
2
AB
a x y z
2
a
2
a
0 0
2
a
Абсолютна величина
вектора ( модуль
вектора, довжина
вектора) дорівнює
кореню квадратному із
суми квадратів його
координат
6. Напрямленість векторів
•Векториі
називають протилежно
напрямленими, якщо
протилежно напрямлені
півпрямі AB і CD .
•Вектори
і
називають
співнапрямленими,
якщо співнапрямлені
півпрямі AB і CD.
7.
Рівні векториb
d
a
• Рівні вектори – це
вектори, що
мають рівні
a b
абсолютні
a b
величини та
однаковий напрям.
• Рівні вектори – це
a b,
вектори, що
xa xb ,
мають рівні
координати.
y y ,
a
b
z a zb
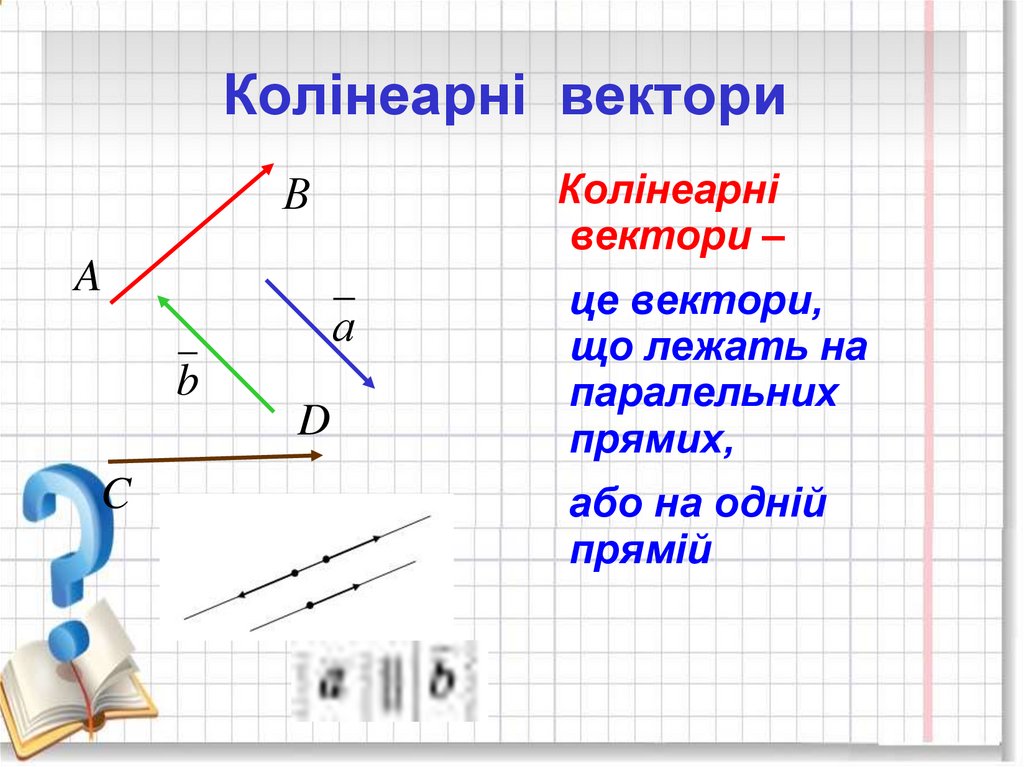
8. Колінеарні вектори
Колінеарнівектори –
В
A
а
b
C
D
це вектори,
що лежать на
паралельних
прямих,
або на одній
прямій
9. Компланарні вектори
Компланарнівектори це вектори, що
лежать
у одній площині,
або
паралельні одній
площині
с
b
a
d
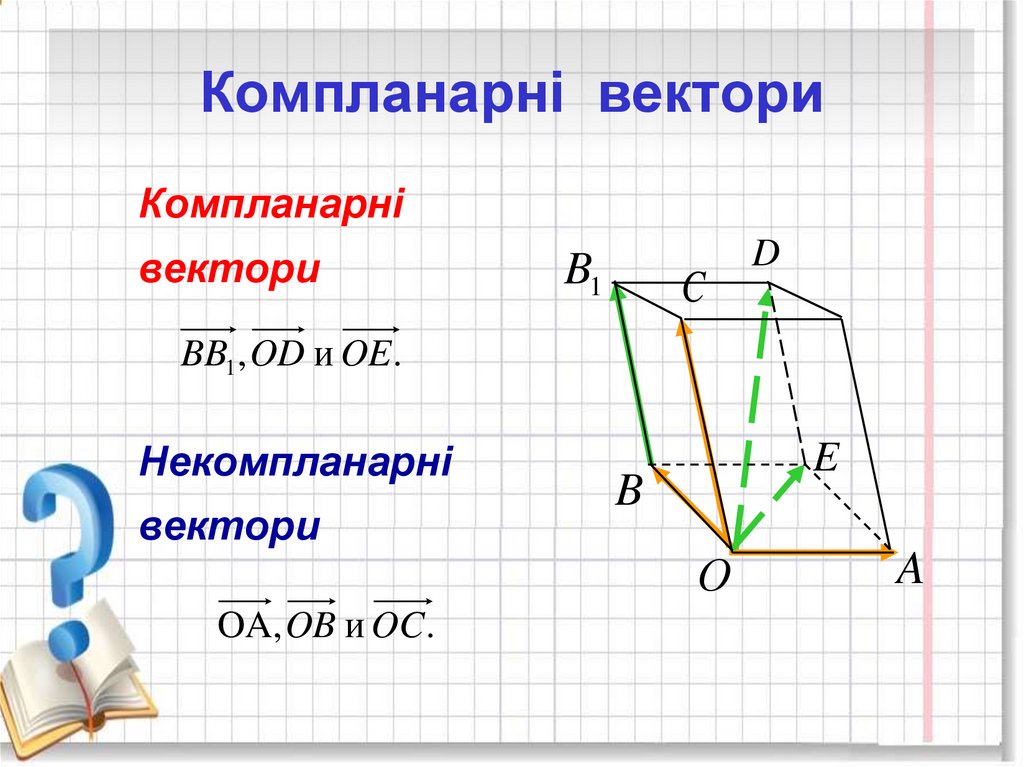
10. Компланарні вектори
Компланарнівектори
B1
C
D
BB1 , OD и OE .
Некомпланарні
вектори
E
B
О
OA, OB и OC.
A
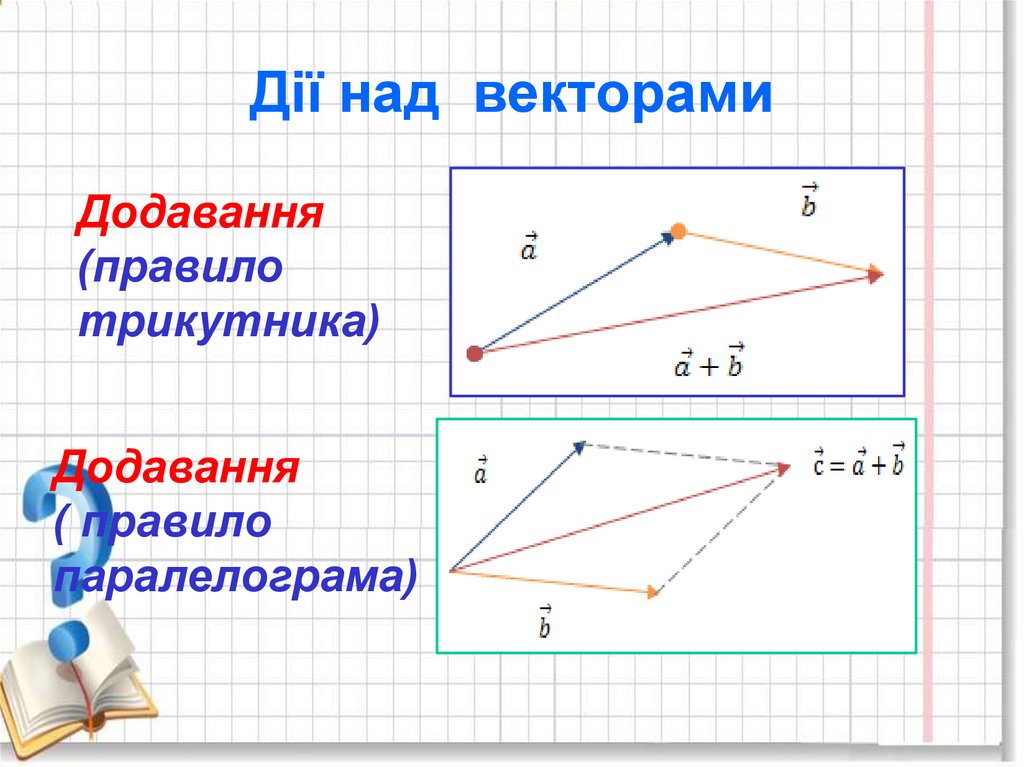
11. Дії над векторами
Додавання(правило
трикутника)
Додавання
( правило
паралелограма)
12. Дії над векторами
Додавання (правилотрикутника)
•За правилом трикутника
обидва вектора
переносяться паралельно
самим собі так, щоб
початок одного з них
збігався з кінцем іншого.
•Вектор суми задається
третьою стороною
трикутника, що утворився,
причому його початок
збігається з початком
першого вектора.
13. Дії над векторами
•За правиломпаралелограма обидва
вектора переносяться
паралельно самим собі
так, щоб їх початки
збігалися.
•Вектор суми задається
діагоналлю побудованого
на них паралелограма, яка
виходить з їх спільного
початку.
Додавання
( правило
паралелограма)
14.
Дії над векторамиДодавання (правило
паралелепіпеда)
C
D
OA OB OC
OD
B
О
A
15. Дії над векторами
Додаванняa xa ; ya ; za b xb ; yb ; zb
xa xb ; ya yb ; za zb
Закони додавання:
1) переставний
2) сполучний
a b b a
( a b) с a ( b c )
16. Дії над векторами
AВіднімання
С
B
AС AB BC
a x a ; y a ; z a b xb ; y b ; z b
x a xb ; y a y b ; z a z b
17. Дії над векторами
•Множення вектора начисло
a xa ; ya ; za
•Якщоa || b
, то
координати векторів
пропорційні.
І навпаки, якщо
координати векторів
пропорційні, то a || b
a
2a
3a
0,5a
xa y a z a
a || b
xb yb zb
18. Скалярний добуток векторів
Скалярним добуткомвекторів називається
сума добутків
відповідних координат
Властивості
скалярного добутку
a b a b cos
a b xa xb ya yb za zb
сos
a b
a b
a a
2
2
a b 0, a 0, b 0 a b

















 mathematics
mathematics








