Вектори у просторі. Дії над векторами

1. Вектори у просторі. Дії над векторами

2.

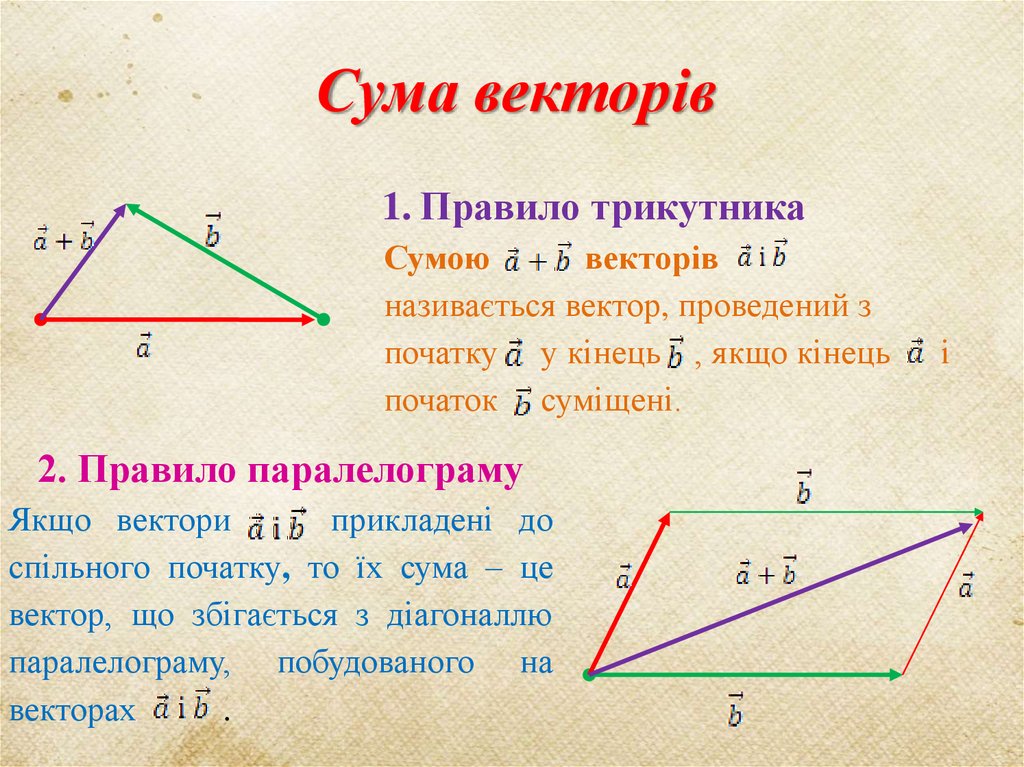
Сума векторів
1. Правило трикутника
Сумою
векторів
називається вектор, проведений з
початку у кінець , якщо кінець
початок суміщені.
2. Правило паралелограму
Якщо вектори
прикладені до
спільного початку, то їх сума – це
вектор, що збігається з діагоналлю
паралелограму, побудованого на
векторах
.
і

3.

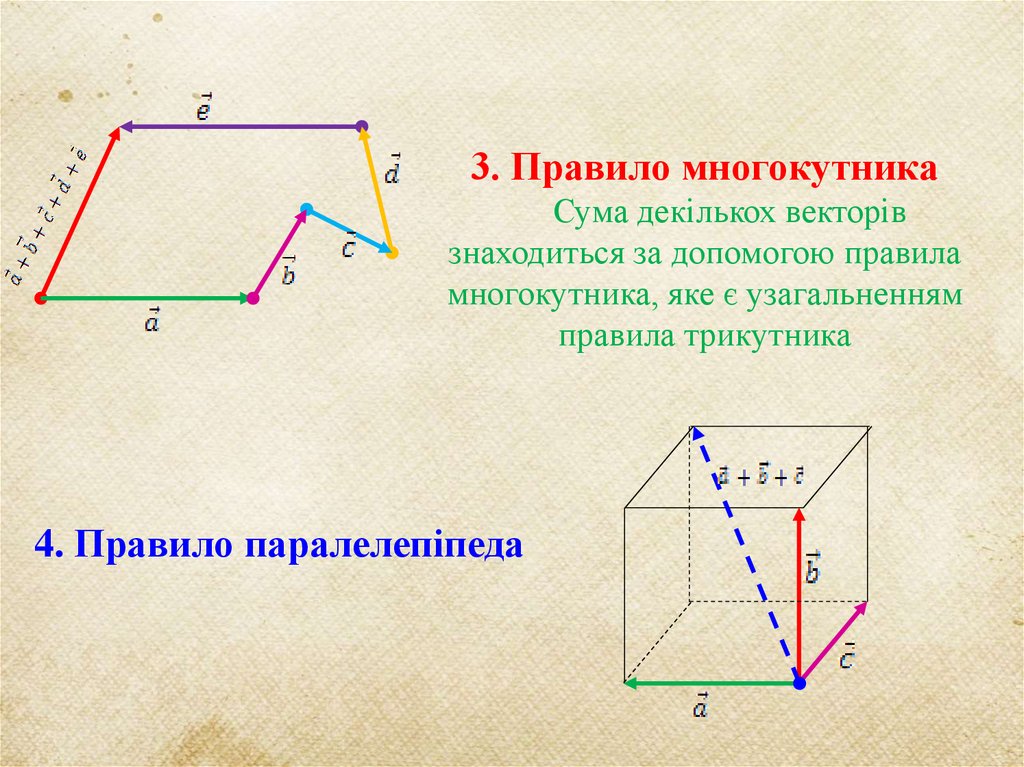
3. Правило многокутника
Сума декількох векторів
знаходиться за допомогою правила
многокутника, яке є узагальненням
правила трикутника
4. Правило паралелепіпеда

4.

Різниця векторів
Різницею
векторів
називається вектор такий, що
Множення вектора на число
Добуток вектора
на число k – це
колінеарний йому вектор
,
співнапрямлений з вектором
, якщо
k >0, і напрямлений протилежно до
нього, якщо k<0. Якщо k=0, то ka=0

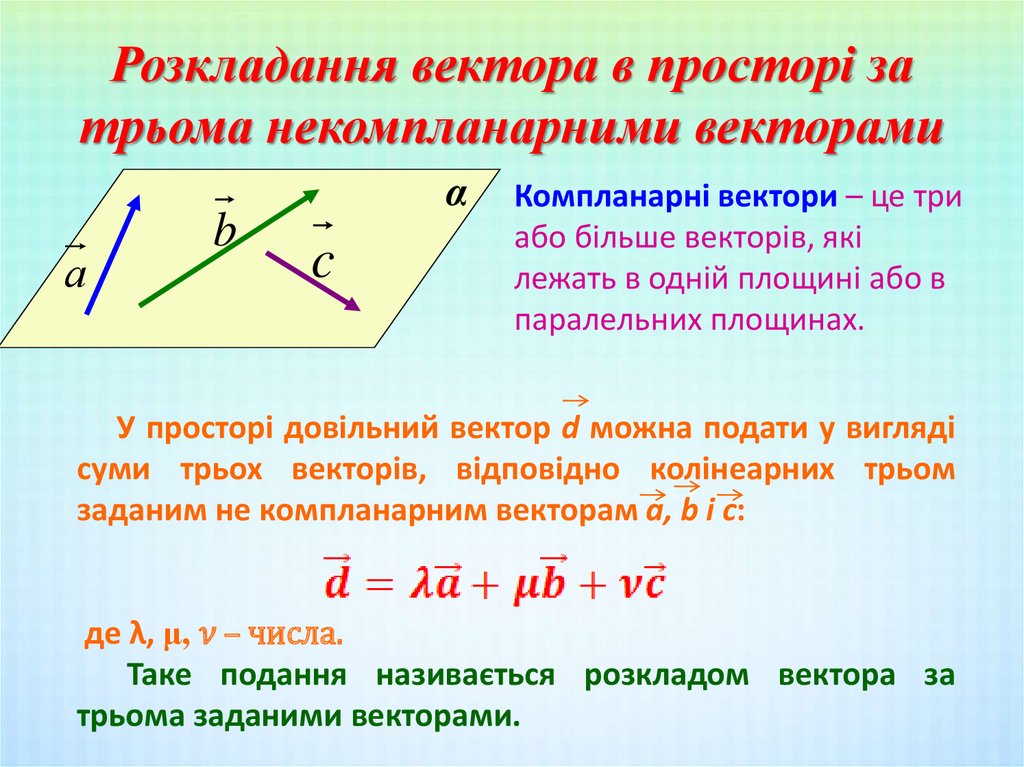
5. Розкладання вектора в просторі за трьома некомпланарними векторами

а
b
α
c
Компланарні вектори – це три
або більше векторів, які
лежать в одній площині або в
паралельних площинах.
У просторі довільний вектор d можна подати у вигляді
суми трьох векторів, відповідно колінеарних трьом
заданим не компланарним векторам a, b i c:
де λ, μ,