Координати та вектори в просторі

1. Координати та вектори в просторі

Серед рівних розумом – за
однакових інших умов переважає
той, хто знає геометрію.
Б.Паскаль

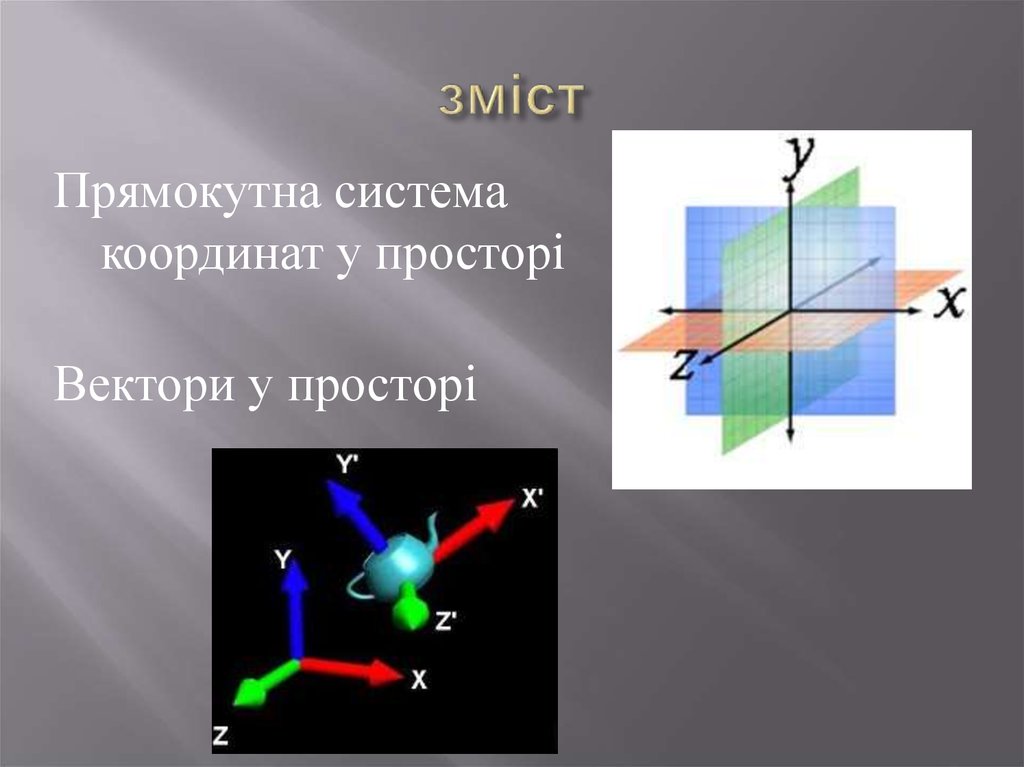
2. зміст

Прямокутна система
координат у просторі
Вектори у просторі

3. Прямокутна система координат у просторі

Декартові координати
у просторі
Відстань між точками
Координати середини
відрізка
Вправи

4. Рене Декарт (1596 – 1650)

Видатний французький
філософ,
математик,
Він числа
і фігури об’єднав,
фізик.
Декарт увів
А лініїфізіолог,
й рівняння
ототожнив,
метод координат, поняття
І людям надпотужний метод дав –
змінної і заклав основи
Такий, що знає нині кожний.
аналітичної геометрії, ввів
Він з геометрією
алгебрустепенів,
здружив,
сучасні позначення
Обох подвоївши
знак
“+”можливості
і
“-” і силу.
для
позначення
додатних
та
Достойно
геній шану
заслужив –
від’ємних
чисел. і стилю.
Творець
нового методу

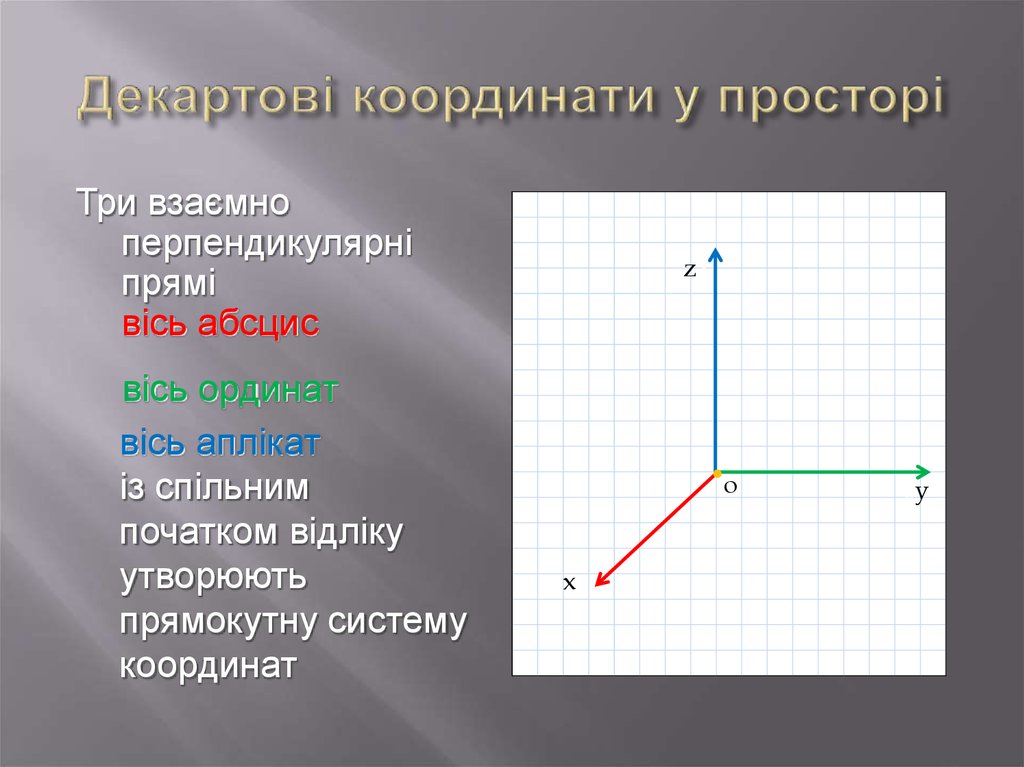
5. Декартові координати у просторі

Три взаємно
перпендикулярні
прямі
вісь абсцис
вісь ординат
вісь аплікат
із спільним
початком відліку
утворюють
прямокутну систему
координат
zz
o
x
ey

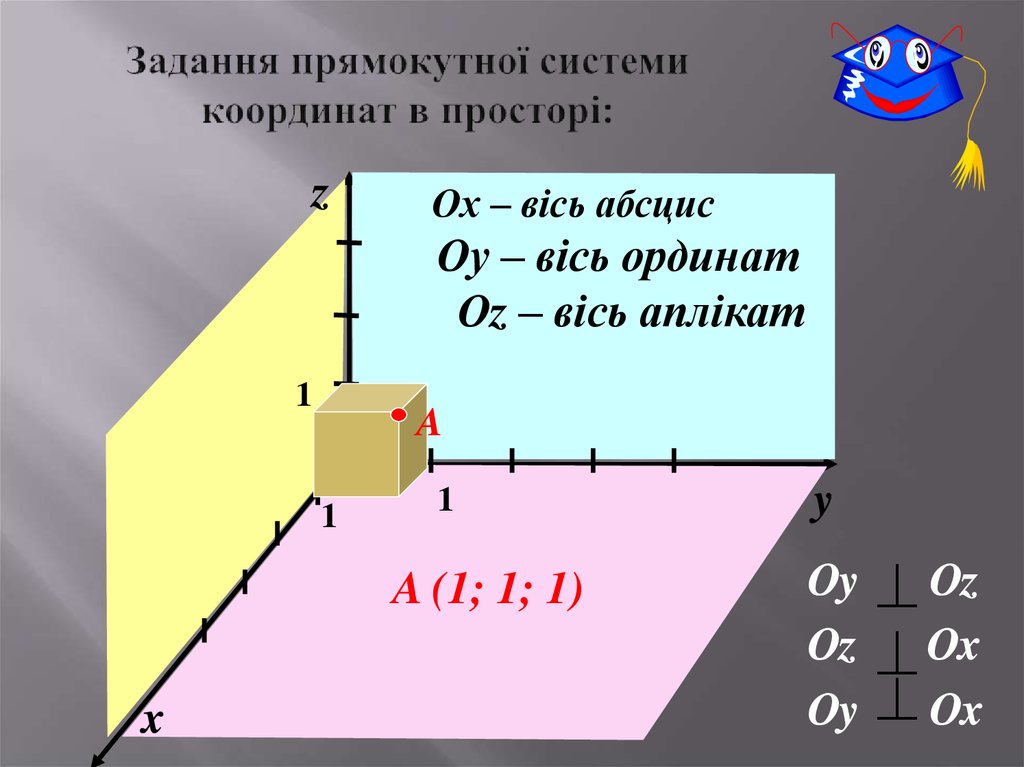
6. Задання прямокутної системи координат в просторі:

z
Ох – вісь абсцис
Оу – вісь ординат
Оz – вісь аплікат
1
A
1
О
1
A (1; 1; 1)
x
y
Оy
Оz
Оy
Оz
Оx
Оx

7.

Координатні площини – хОу, yOz, хОz –
поділяють простір на октанти. Знаки
координат залежать від октанта, у якому
міститься точка простору.

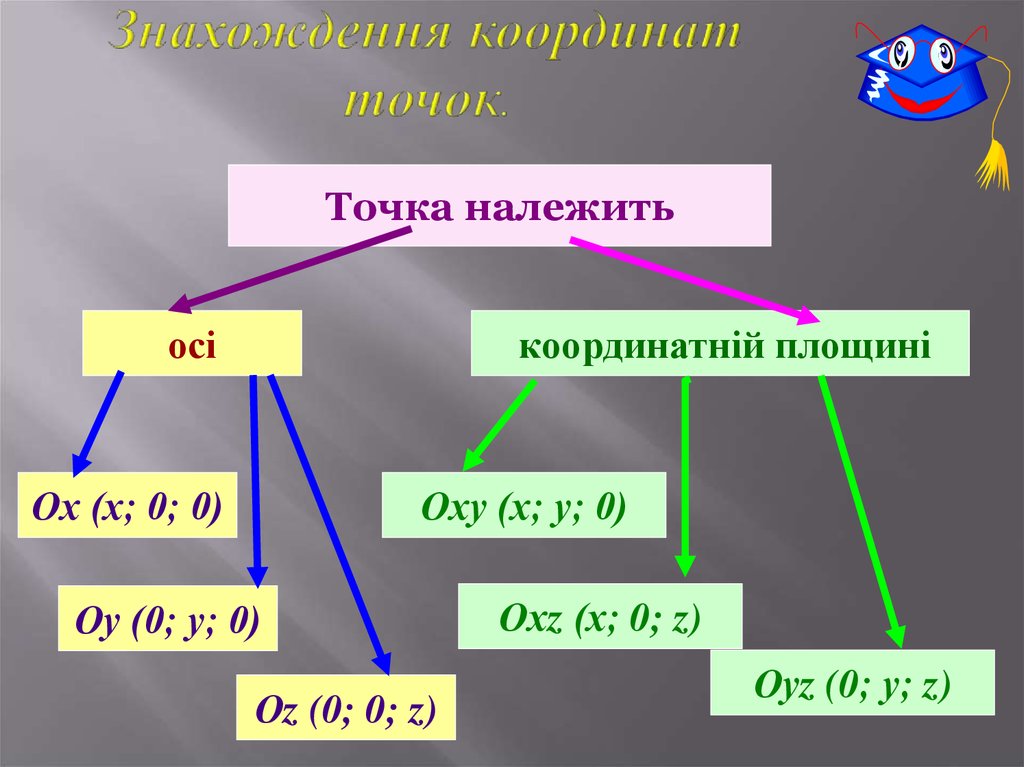
8. Знахождення координат точок.

Точка належить
осі
координатній площині
Ох (х; 0; 0)
Оху (х; у; 0)
Оу (0; у; 0)
Оz (0; 0; z)
Охz (х; 0; z)
Оуz (0; у; z)

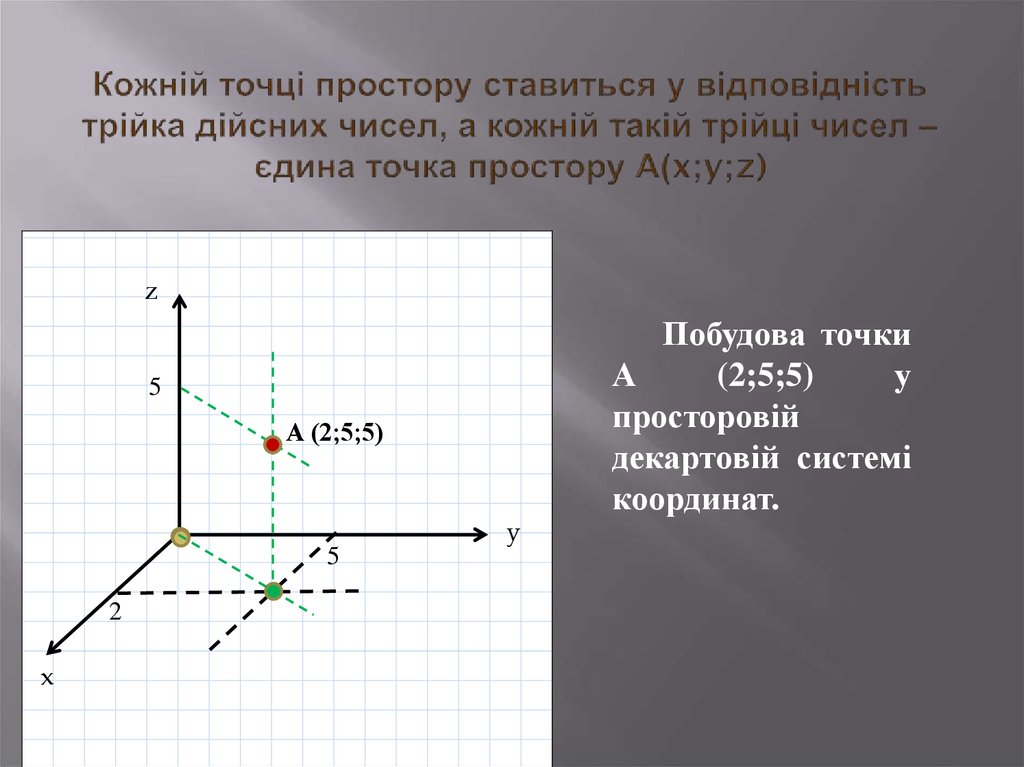
9. Кожній точці простору ставиться у відповідність трійка дійсних чисел, а кожній такій трійці чисел – єдина точка простору А(x;y;z)

z
5
А (2;5;5)
5
2
x
y
Побудова точки
А
(2;5;5)
у
просторовій
декартовій системі
координат.

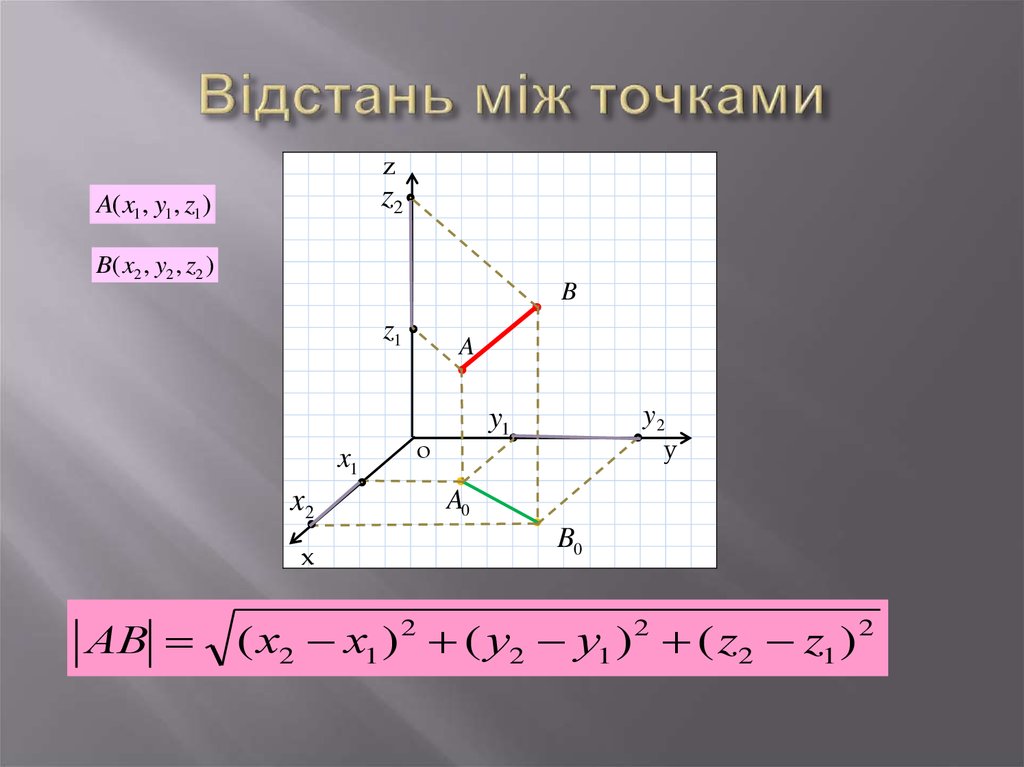
10. Відстань між точками

z
z2
A( x1, y1, z1 )
B( x2 , y2 , z2 )
B
z1
x1
x2
x
АВ
A
y2
y1
o
y
A0
B0
( х2 х1 ) 2 ( у2 у1 ) 2 ( z2 z1 ) 2

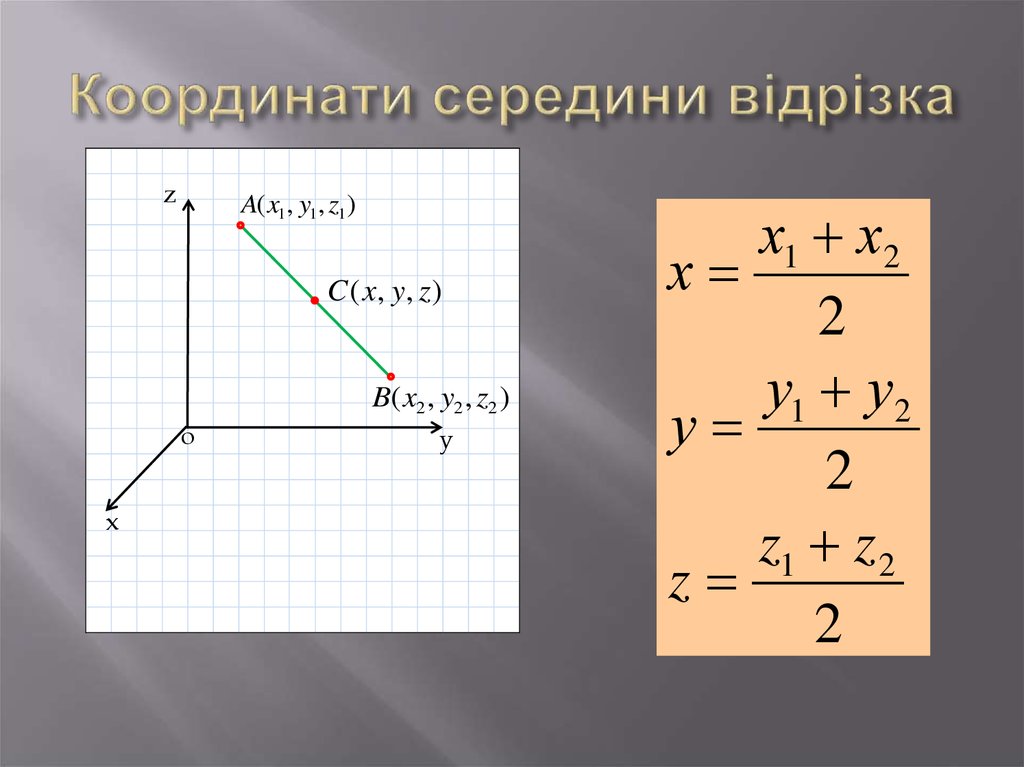
11. Координати середини відрізка

z
A( x1, y1, z1 )
C ( x, y , z )
B( x2 , y2 , z2 )
o
x
y
х1 х2
х
2
у1 у2
у
2
z1 z 2
z
2

12. Вектори у просторі

Дещо з історії вектора
Означення вектора
Координати вектора
Довжина вектора
Види векторів
Рівні вектори
Операції над векторами
Властивості операцій додавання векторів
Кут між векторами
Скалярний добуток
Вправи

13. Дещо з історії вектора

Вектор - відносно нове
математичне поняття. Термін
вектор
(від латинського
vector – «несучий») уперше
з’явився в 1845році у працях
із побудови числових систем,
які
узагальнювали
комплексні
числа,
ірландського математика й
астронома
Уільяма
Гамільтона (1805-1865). Саме
Гамільтону належать терміни
«скаляр»,
«скалярний
добуток»,
«векторний
добуток».

14. Дещо з історії вектора

Майже
одночасно
з
Гамільтоном дослідження
у цьому напрямі, але з
іншої
точки
зору,
проводив
німецький
математик
Герман
Грассман (1809 - 1887)

15. Дещо з історії вектора

Англійський математик
Уїльям Кліффорд (18451879) зумів об’єднати два
підходи в загальній теорії,
яка включала в себе і
звичайне
векторне
числення.

16. Дещо з історії вектора

Остаточного
вигляду
векторне числення набуло
в працях американського
фізика
і
математика
Джозайя Уілларда Гіббса
(1839-1903), який у 1901
році
опублікував
ґрунтовний підручник з
векторного аналізу.

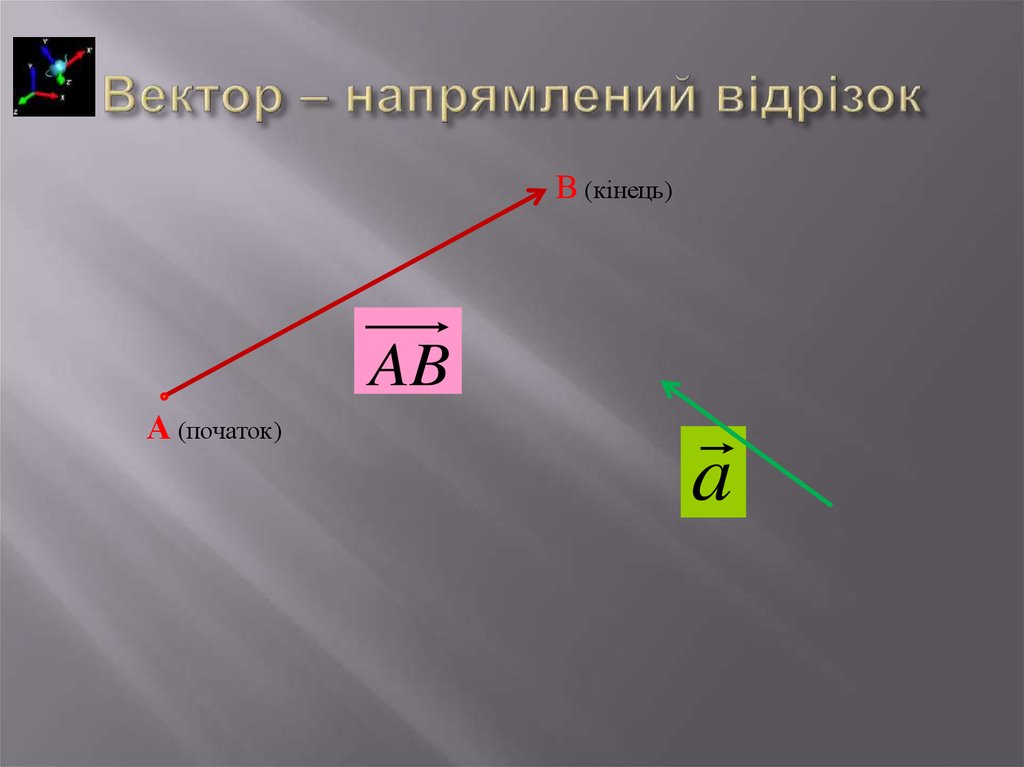
17. Вектор – напрямлений відрізок

В (кінець)
AB
А (початок)
a

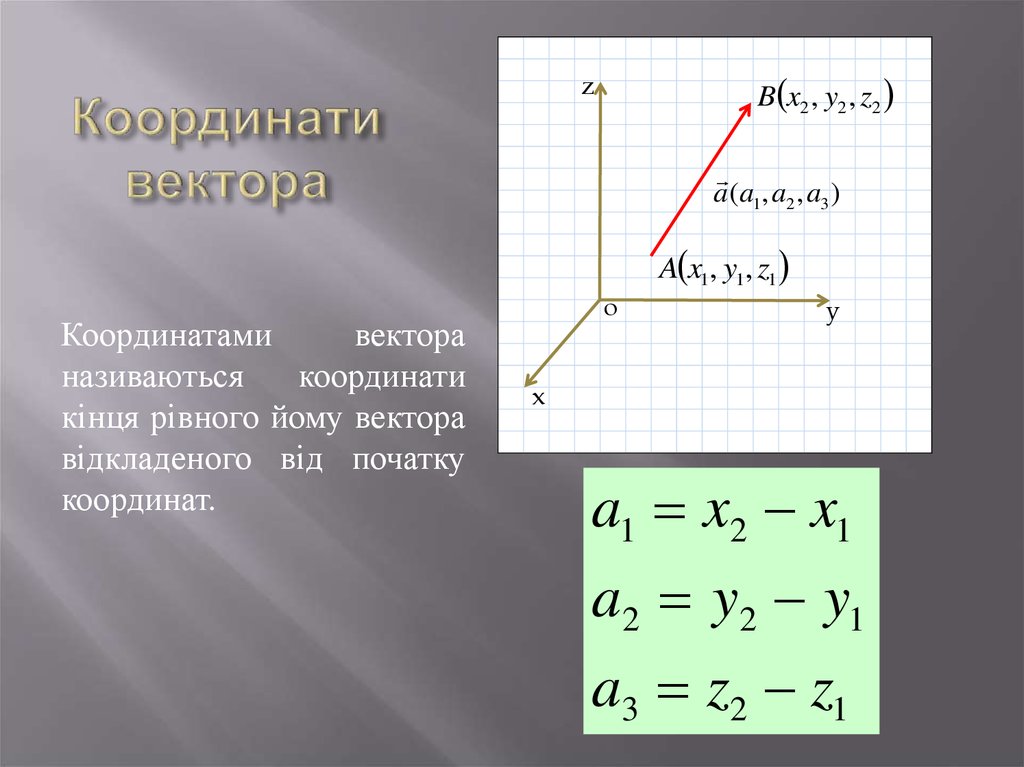
18. Координати вектора

B x2 , y2 , z2
z
a (a1, a2 , a3 )
A x1, y1, z1
Координатами
вектора
називаються
координати
кінця рівного йому вектора
відкладеного від початку
координат.
o
y
x
a1 x2 x1
a2 y2 y1
a3 z2 z1

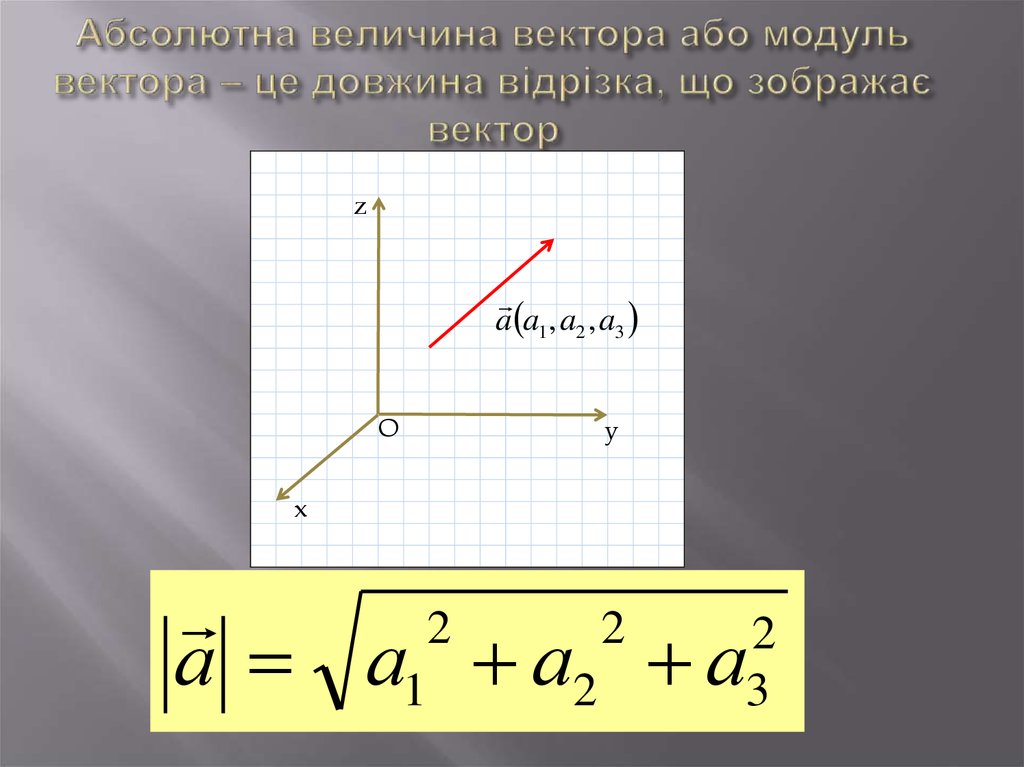
19. Абсолютна величина вектора або модуль вектора – це довжина відрізка, що зображає вектор

z
a a1, a2 , a3
O
y
x
2
2
2
а а1 а2 а3

20.

Протилежні вектори
Колінеарні вектори
Компланарні вектори
Види
векторів
Одиничний вектор
Вектори-орти
Нульовий вектор

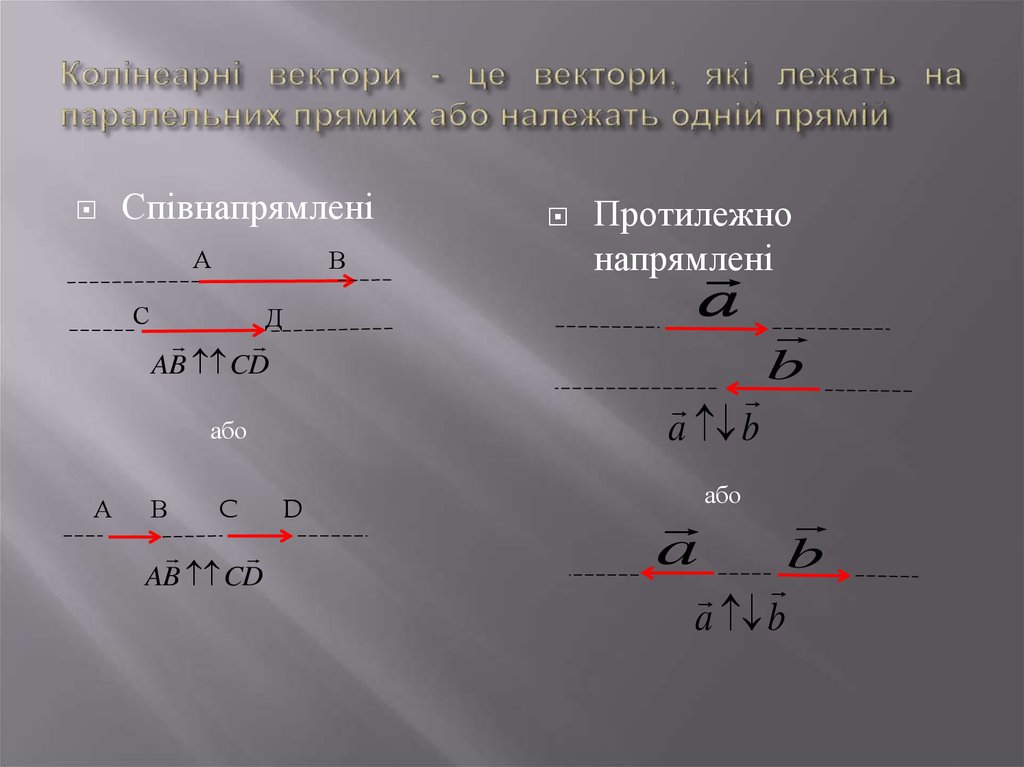
21. Колінеарні вектори - це вектори, які лежать на паралельних прямих або належать одній прямій

Співнапрямлені
А
С
В
AB CD
В
C
AB CD
Протилежно
напрямлені
a
Д
a b
або
А
D
a
b
або
a b
b

22. Умова колінеарності векторів

Вектори колінеарні b a
b1 b2 b3
a1 a2 a3
(відповідні координати пропорційні)
Вектори з координатами (2;4;-6) та (1;2;-3) колінеарні, тому що
2 4 6
1 2 3

23. Рівні вектори

Два вектори називаються рівними, якщо вони
мають рівні модулі і однаково напрямлені.
a
b
| a | | b |
Якщо вектори задані координатами, то
a1 b1
а (а1 , а2 , а3 ) b (b1 , b2 , b3 ) a2 b2
a b
3
3

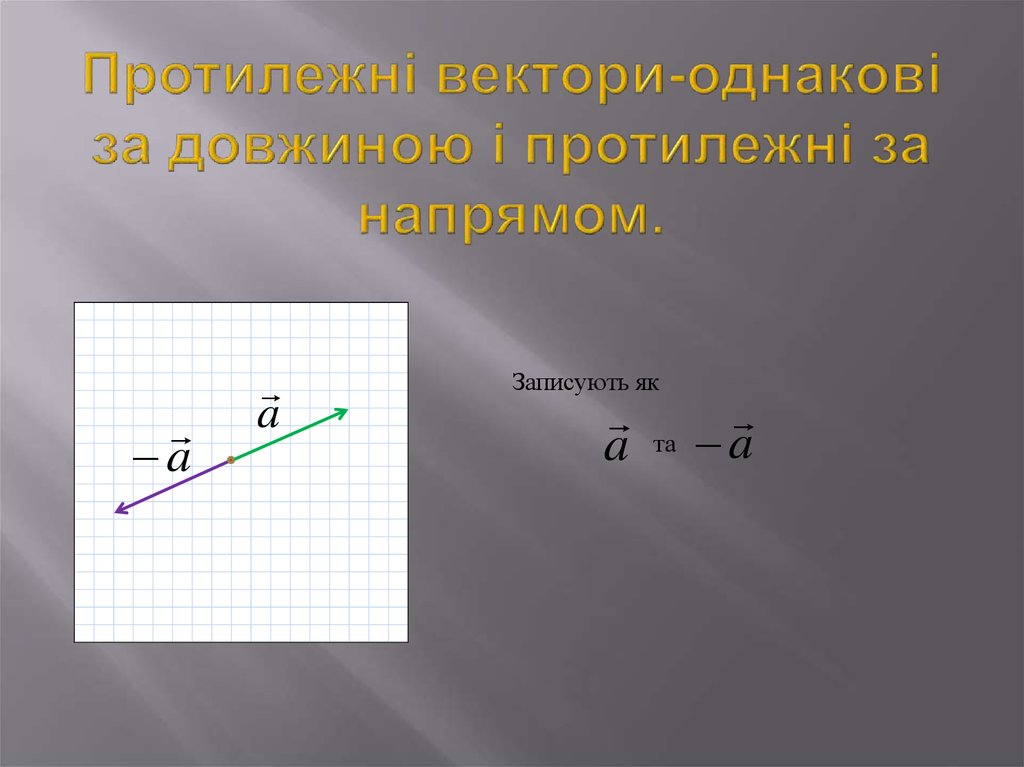
24. Протилежні вектори-однакові за довжиною і протилежні за напрямом.

a
a
Записують як
a
та
a

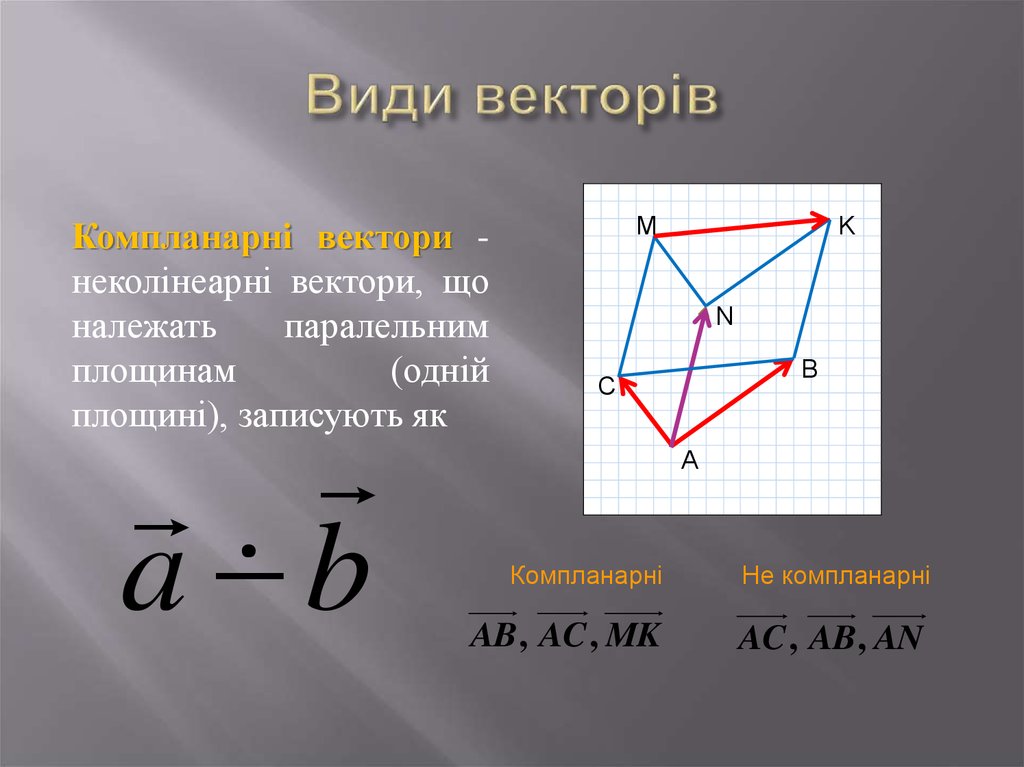
25. Види векторів

Компланарні вектори неколінеарні вектори, що
належать
паралельним
площинам
(одній
площині), записують як
a b
M
K
N
B
C
A
Компланарні
Не компланарні
AB, AC , MK
AC , AB, AN

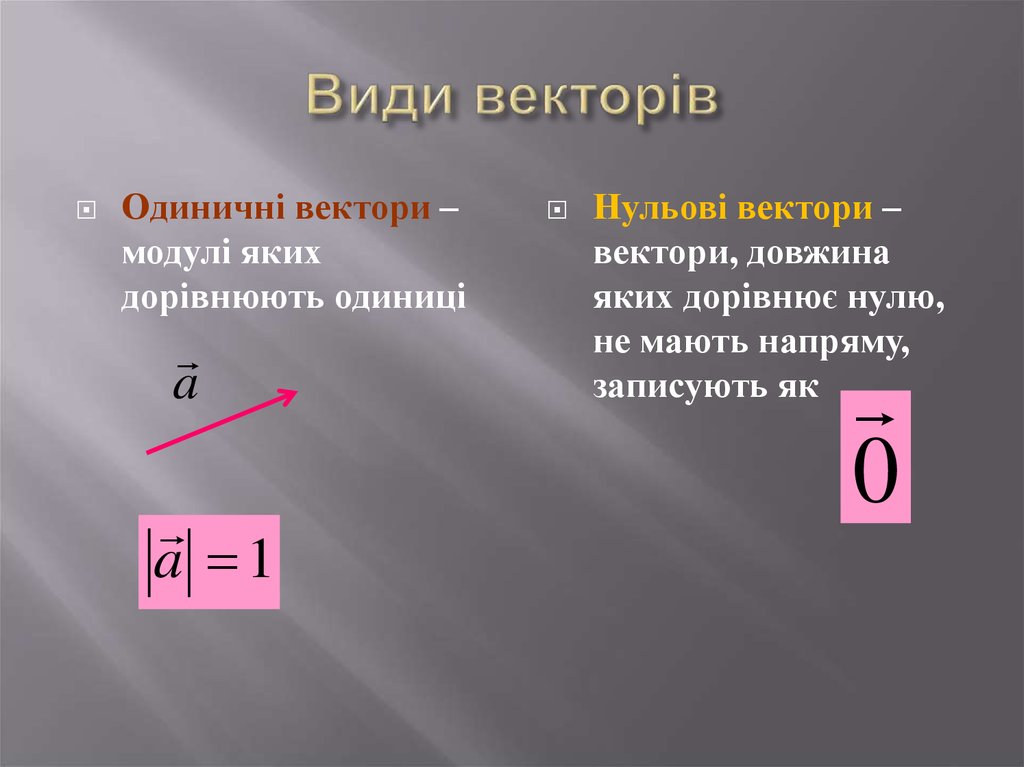
26. Види векторів

Одиничні вектори –
модулі яких
дорівнюють одиниці
a
a 1
Нульові вектори –
вектори, довжина
яких дорівнює нулю,
не мають напряму,
записують як
0

27. Види векторів

Координатні вектори, або орти, - одиничні
вектори,
напрями яких збігаються з напрямами осей координат.
Орти паралельні напряму осей ОХ, ОУ, OZ прямокутної
системи координат, зазвичай їх позначають як
e1 , e2 , e3
z
e3
e1
х
o
e2
у

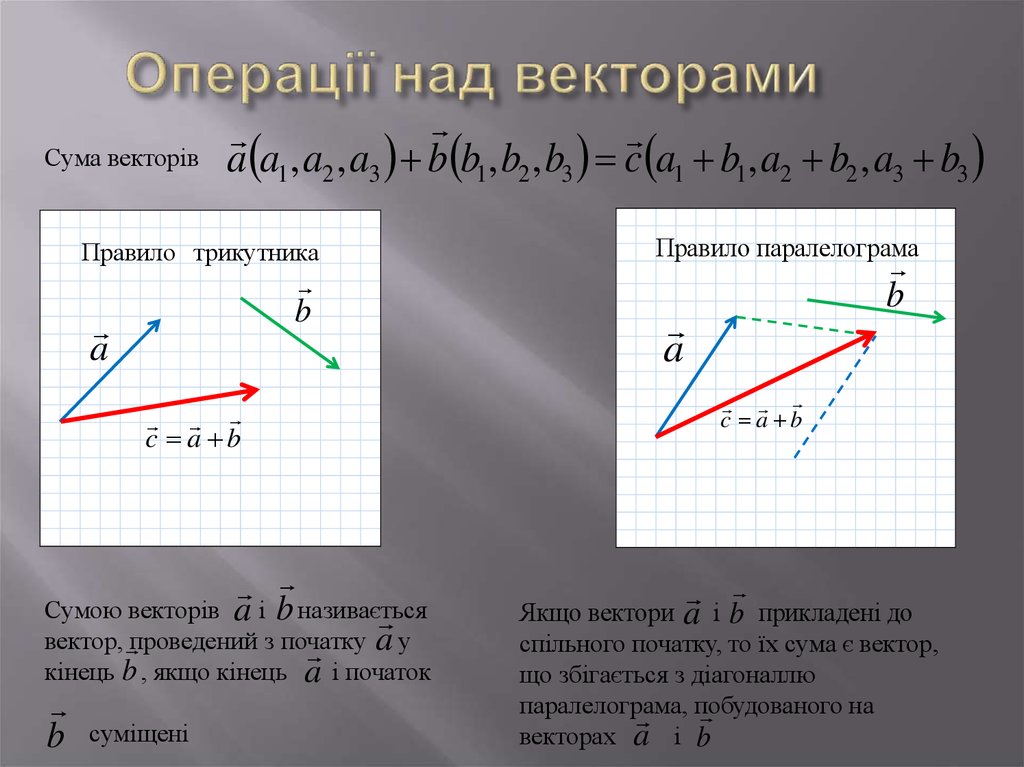
28. Операції над векторами

Сума векторів
a a1, a2 , a3 b b1, b2 , b3 c a1 b1, a2 b2 , a3 b3
Правило трикутника
b
a
c a b
Сумою векторів a і b називається
вектор, проведений з початку
aу
кінець b , якщо кінець a і початок
b
суміщені
Правило паралелограма
b
a
c a b
Якщо вектори a і b
прикладені до
спільного початку, то їх сума є вектор,
що збігається з діагоналлю
паралелограма,
на
побудованого
векторах a і b

29. Операції над векторами

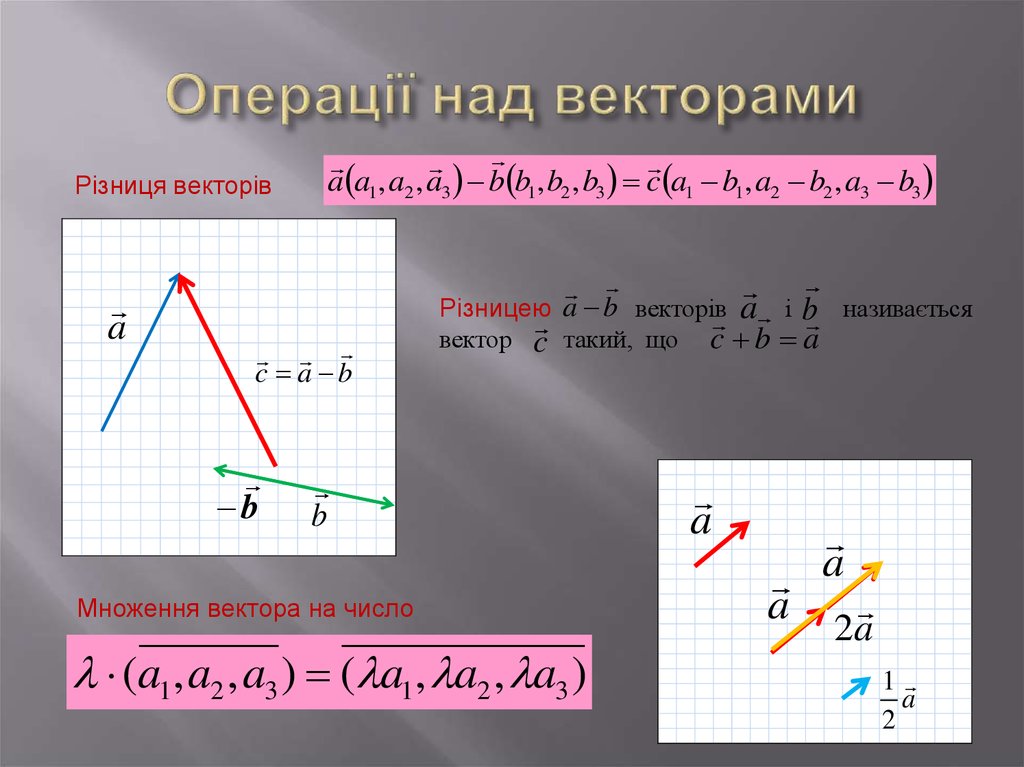
Різниця векторів
a
a a1, a2 , a3 b b1, b2 , b3 c a1 b1, a2 b2 , a3 b3
c a b
b
Різницею a b векторів
вектор
c
такий, що
b
Множення вектора на число
(a1, a2 , a3 ) ( a1, a2 , a3 )
a і b
c b a
a
називається
a
a
2a
1
a
2

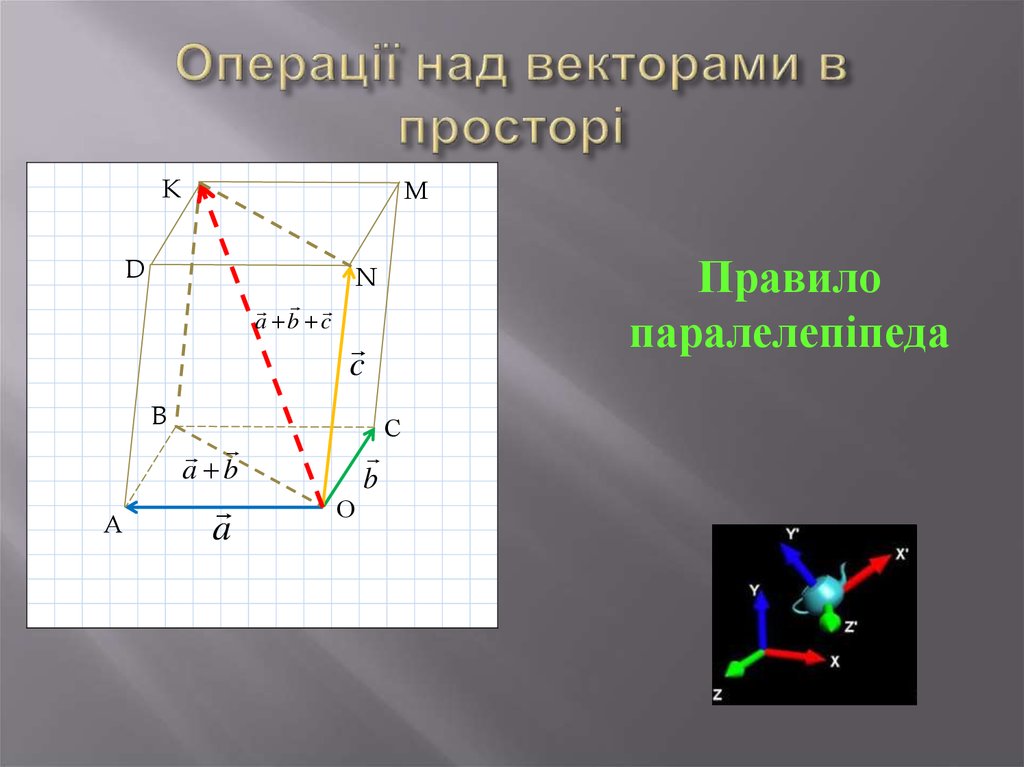
30. Операції над векторами в просторі

K
М
D
a b c
B
А
c
a b
a
Правило
паралелепіпеда
N
О
b
С

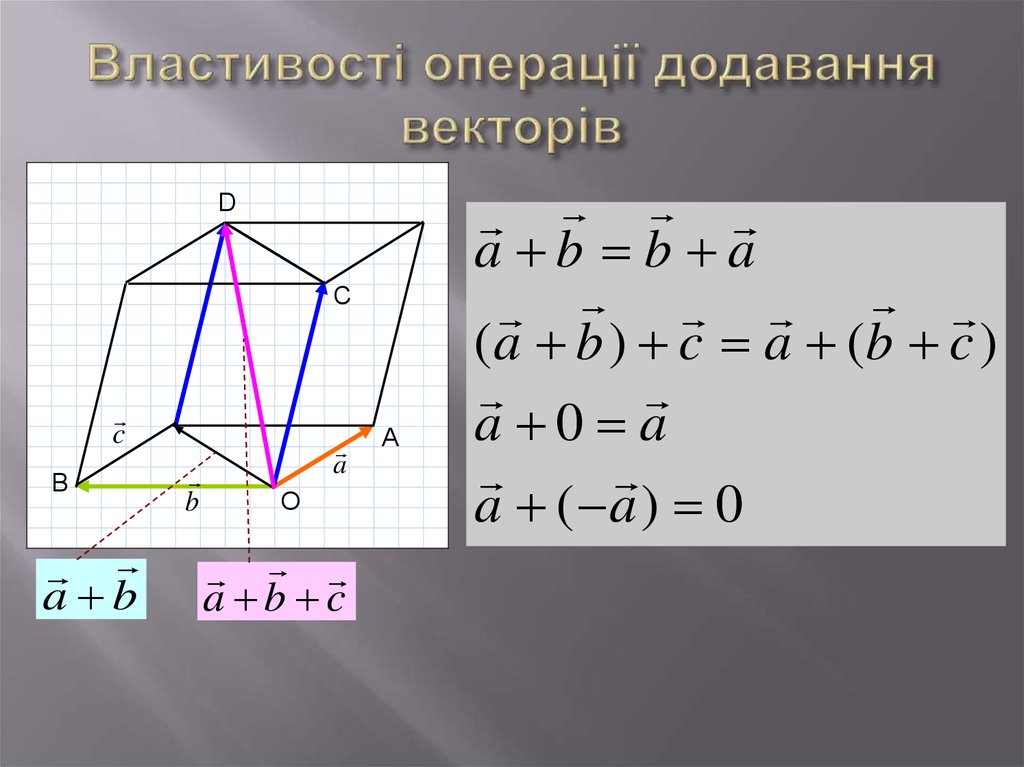
31. Властивості операції додавання векторів

D
С
c
В
a b
b
a
О
a b c
А
a b b a
( a b ) c a (b c )
a 0 a
a ( a ) 0

32. Кут між векторами

Кутом між векторами називається кут між
векторами, рівними даним і такими, що мають
спільний початок.
a, b
a
a
b
b

33. Скалярний добуток

a
Скалярним добутком ненульових векторів
і
називається число, що дорівнює добутку довжин
цих векторів на косинус кута між ними
Якщо a b 0, то
Якщо a b 0, то
a
a b a b cos
– гострий
– тупий
a a1, a2 , a3 , b b1, b2 , b3
b
b
Якщо
добуток
векторів
дорівнює
однойменних координат
, то скалярний
сумі
добутків
a b a1b1 a2b2 a3b3
Умова перпендикулярності векторів:
при
a 0, b 0
a b 0 a b

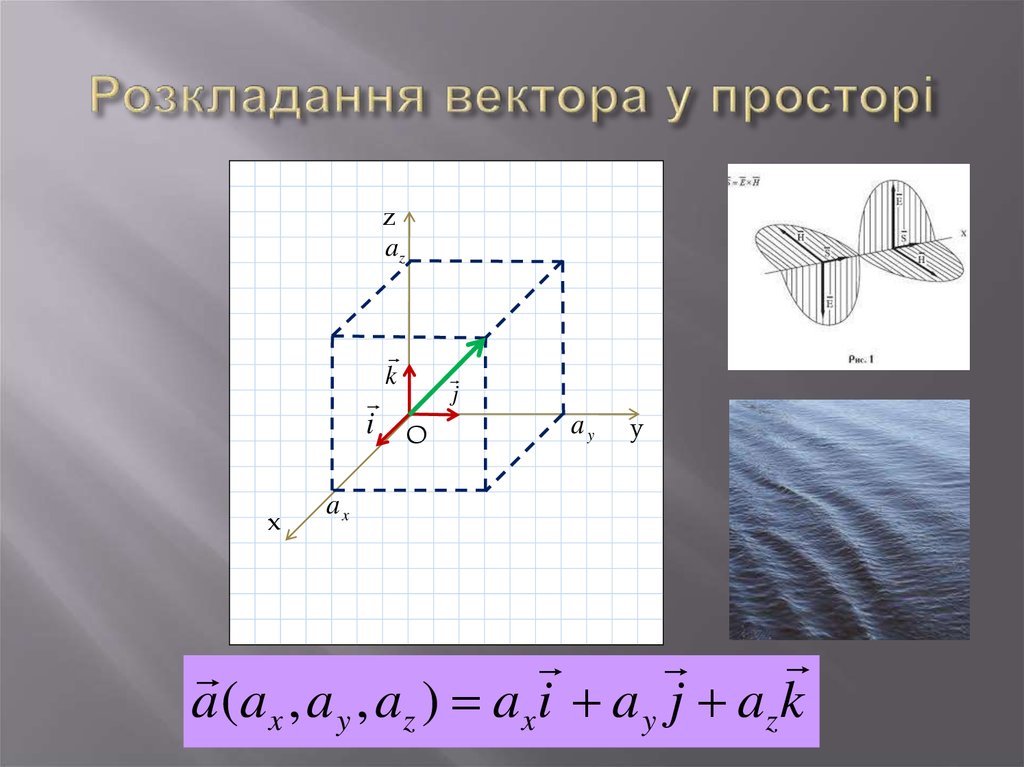
34. Розкладання вектора у просторі

z
az
k
i O
x
j
ay
y
ax
a (a x , a y , az ) a x i a y j az k

35.

Якщо хочеш досягнути
У житті своїм вершин,
математику збагнути
Мусиш тонко до глибин.
Якщо хочеш бізнесменом
після школи,друже, стать,
Аксіоми й теореми
мусиш добре пам’ятать.
Не махай на все рукою,
не лінуйся, а учись.
Бо чого навчишся в школі,
Знадобиться ще колись.

36.

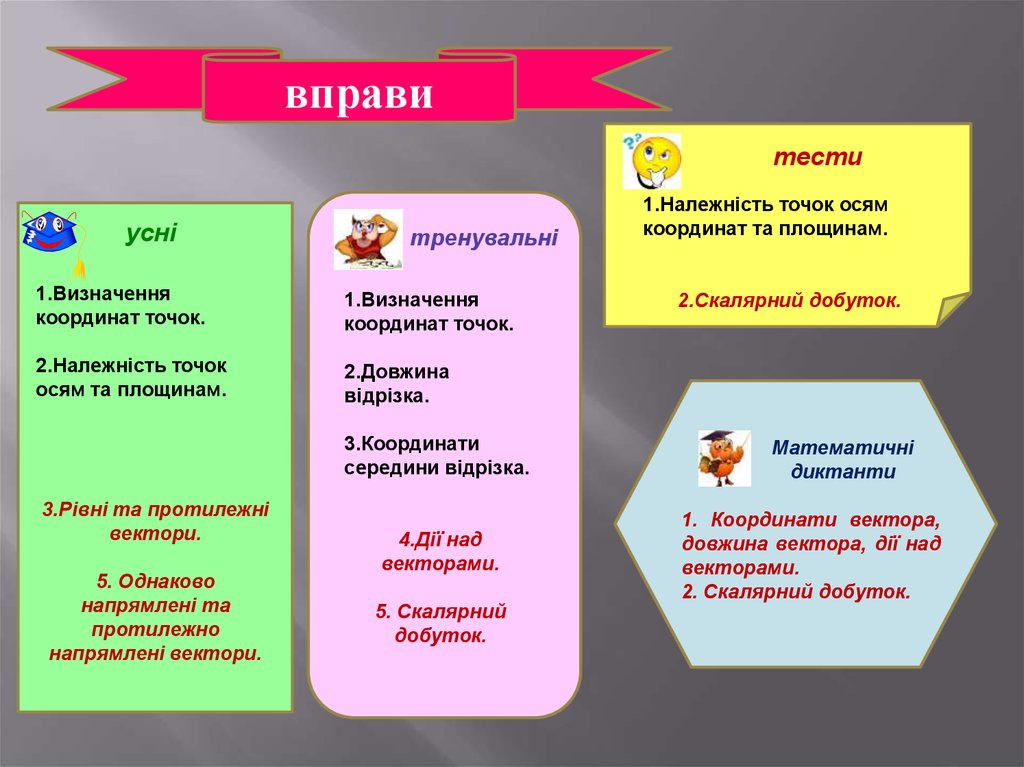
вправи
тести
усні
тренувальні
1.Визначення
координат точок.
1.Визначення
координат точок.
2.Належність точок
осям та площинам.
2.Довжина
відрізка.
3.Координати
середини відрізка.
3.Рівні та протилежні
вектори.
5. Однаково
напрямлені та
протилежно
напрямлені вектори.
4.Дії над
векторами.
5. Скалярний
добуток.
1.Належність точок осям
координат та площинам.
2.Скалярний добуток.
Математичні
диктанти
1. Координати вектора,
довжина вектора, дії над
векторами.
2. Скалярний добуток.

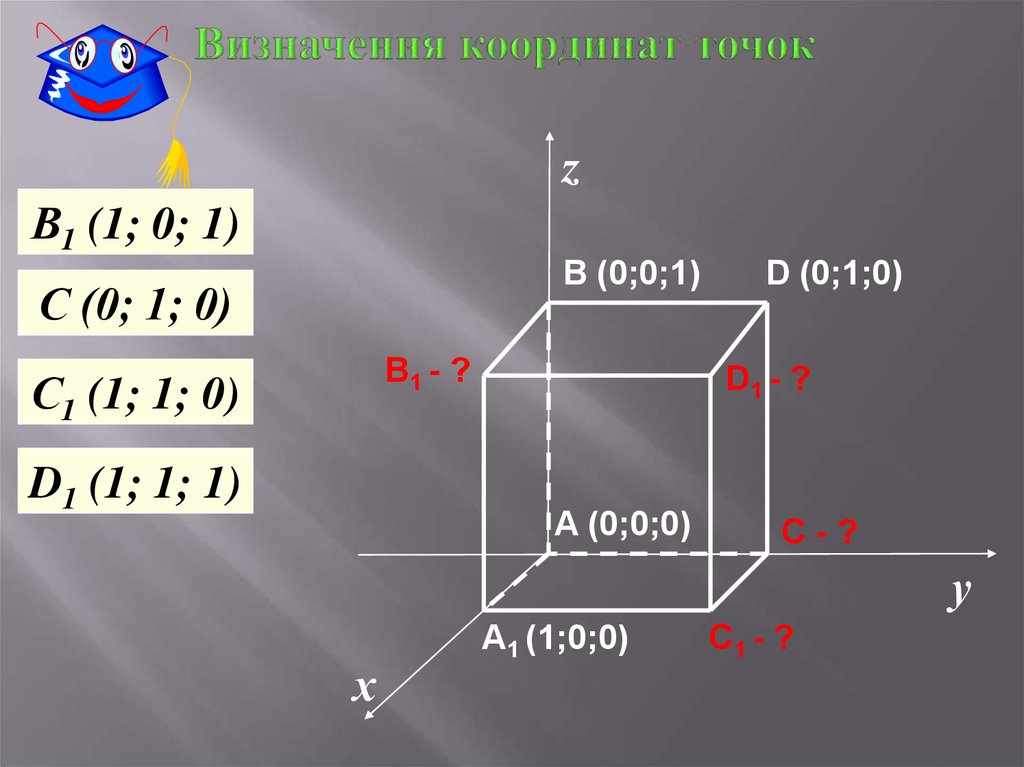
37. Визначення координат точок

z
В1 (1; 0; 1)
B (0;0;1)
С (0; 1; 0)
B1 - ?
С1 (1; 1; 0)
D1 (1; 1; 1)
D (0;1;0)
D1 - ?
A (0;0;0)
C-?
у
х
A1 (1;0;0)
C1 - ?

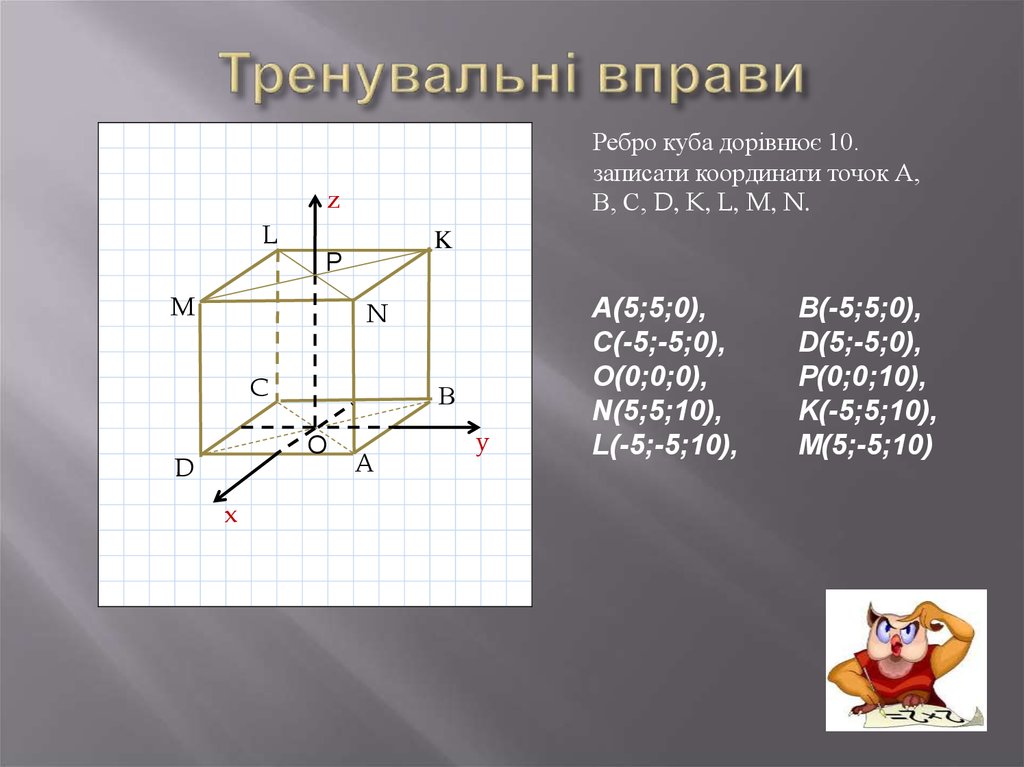
38. Тренувальні вправи

Ребро куба дорівнює 10.
записати координати точок А,
В, С, D, K, L, M, N.
z
L
K
P
M
N
C
В
O
D
x
A
y
А(5;5;0),
C(-5;-5;0),
O(0;0;0),
N(5;5;10),
L(-5;-5;10),
B(-5;5;0),
D(5;-5;0),
P(0;0;10),
K(-5;5;10),
M(5;-5;10)

39. Усні вправи

З-поміж точок А(2;0;-4), В(3;0;0),
С(0;5;0), D(-2;9;0), Е(0;0;13)
1.Виберіть ту,
яка належить
- осі аплікат;
- осі ординат.
2.Виберіть ту,
яка не належить
жодній із
координатних
площин.

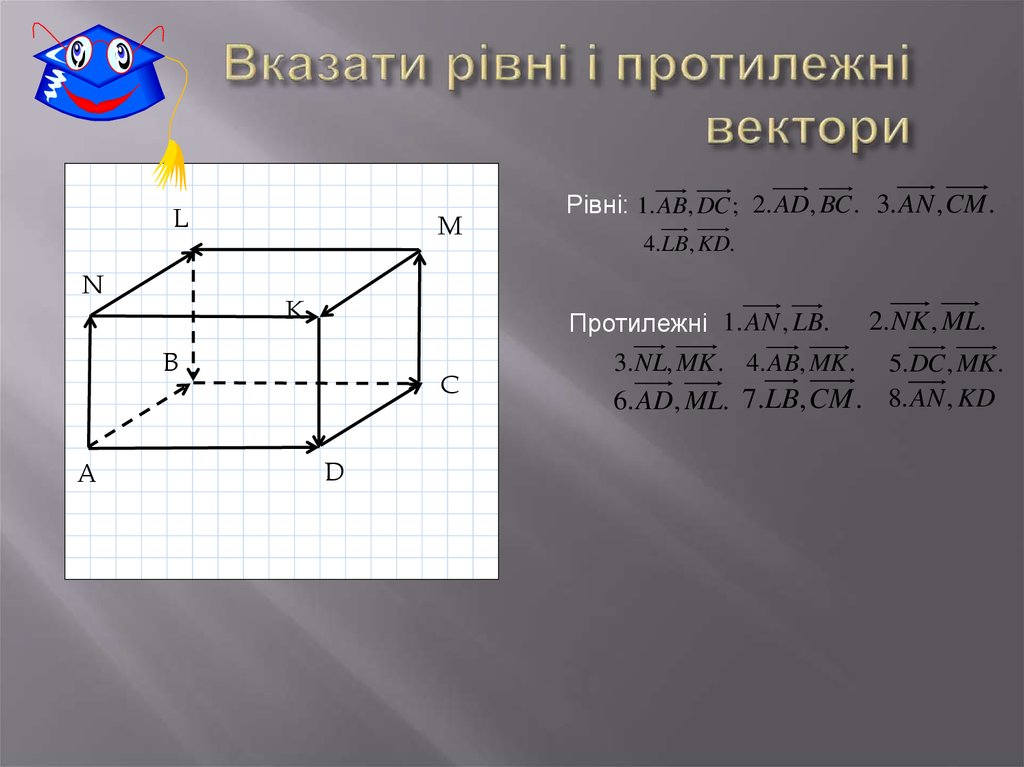
40. Вказати рівні і протилежні вектори

L
N
M
K
4.LB, KD.
Протилежні 1. AN , LB.
B
A
Рівні: 1. AB, DC ; 2. AD, BC . 3. AN , CM .
C
D
3. NL, MK . 4. AB, MK .
2. NK , ML.
5.DC , MK .
6. AD, ML. 7.LB, CM . 8. AN, KD

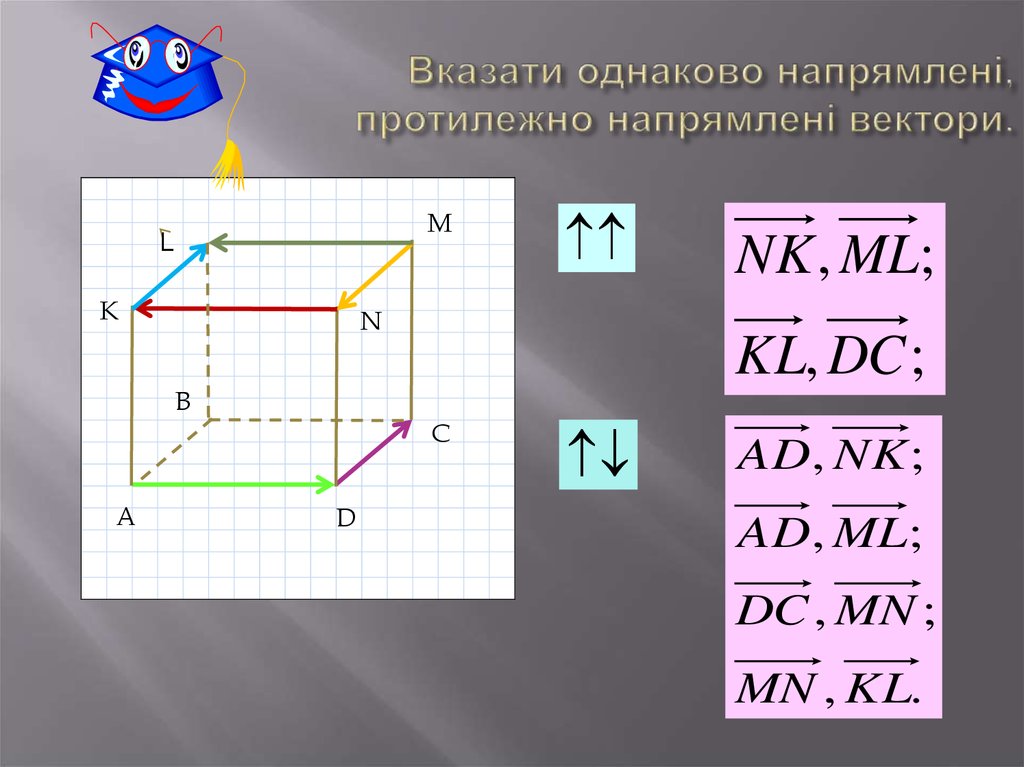
41. Вказати однаково напрямлені, протилежно напрямлені вектори.

M
L
K
N
NK , ML;
KL, DC ;
B
C
A
D
AD, NK ;
AD, ML;
DC , MN ;
MN , KL.

42. Тренувальні вправи

1. Знайдіть відстань АВ, якщо А(-1;3;-1), В(-1;0;5)
2. Знайдіть відстань від точки А(-1;2;-2) до
початку координат.
3. Знайдіть периметр трикутника АВС, якщо
А(7;1;-5), В(4; - 3; - 4), С(1; 3; - 2)
Відповіді: 1.АВ=5, 2. ОА=3, 3. P 14
26

43. Тренувальні вправи

1.Які координати середини С відрізка АВ, якщо А(0;2;11), В(2;0;-1).
С(1;1;-6)
2.Дано С(2;6;3),А(4;2;1). Знайдіть координати точки В,
якщо відомо, що АС=ВС і точки А, В, С лежать на одній
прямій.
В(0;10;5)
3. Знайдіть координати середин сторін трикутника АВС,
якщо А(2;0;2), В(2;2;0), С(2;2;2).
(2;2;1),(2;1;),(2;1;1)
Знайдіть довжину медіани АМ трикутника АВС, якщо
А(2;1;3), В(2;1;5), С(0;1;1)
АМ=1

44. Тренувальні вправи “дії з векторами”

a
Знайти
(4;-5;6), b (-1;2;5).
1) a b
2) a b
2. Дано
a (1;-2;3), b (-2;1;-3).
1.Дано
Знайти координати
векторів
1) 2 a ,
2) 3b ,
1) (3;-3;11);
2) (5;-7;1).
3) 2 a +3 b
1) (2;-4;5);
2) (-6;3;-9);
3) (-4;-1;-3).

45. Тренувальні вправи “скалярний добуток”

1.Знайдіть скалярний добуток двох векторів, якщо |a |=5, | b |=4, а кут
між векторами дорівнює 120
10
a (2;3;6), b (3;2;-1).
2. Чи перпендикулярні вектори
ні
3. При якому значенні m вектори
перпендикулярні ?
4. Знайдіть кут між векторами
a (6;0;12), b (-8;13;m)
a (1;1;0),
4
b (1;0;1)
60

46. Математичний диктант по темі: “Координати вектора, Довжина вектора, Дії над векторами”

Дано вектори:
варіант 1 - a (3;0;4); b (7;0;2)
варіант 2 - a (2; 2;0); b (3;0; 3)
Запишіть: 1)координати вектора с, якщо
c a b
2) координати вектора d , якщо d 2a b ,
3) довжину вектора a b ,
4) координати вектора m, якщо відомо, що
довжина вектора m втричі більша довжини
вектора a
5) при якому значенні k вектор n (k ;0;6)
колінеарний вектору b ,
6) чи компланарні вектори a , b , j (0;0;1)

47. відповідь

Варіант 1: 1) c (10;0;6) ; 2) d ( 1;0;6) ; 3) 2 34 ;
4) m( 9;0; 12), m(9;0;12) ; 5) k 21; 6) так.
Варіант 2: 1) c (5; 2; 3) ; 2)d (1; 4;3) ; 3) 38;
4) m(6; 6;0), m( 6;6;0) ; 5) k 6 ; 6) ні.

48. Математичний диктант по темі: “скалярний добуток”

У просторі дано вектори a (1;1;0), b (0;1;1).
Укажіть, які з вказаних тверджень правильні, а
які – неправильні.
А) довжини векторів a і b рівні;
б) скалярний добуток векторів
і b дорівнює 2;
a
;
в) кут між
векторами
і
дорівнює
120
b
a
г) ( a b )( a b ) 0 ;
д) (a b )і (a b ) перпендикулярні
a) “+”; б) “-”;
в) “-”;
г) “+”;
д) “+”.

49. Тестові вправи належність точок осям координат та площинам

1.Яка з наведених точок належить координатній осі Ох ?
А) А(1;-5;0), Б) В(5;0;-4), В) С(-9;0;0), Г) D(0;-8;0)
2.Яка з наведених точок належить координатній площині хz ?
A) A(0;-7;0), Б) В(4;0;-1), В) С(3;-4;3), Г) D(0;9;1)
3.Яка з наведених точок належить координатній осі Оу ?
А.(2;0;-3)
Б.В(0;-4;0)
В.С(3;1;-1)
Г. D(0;9;1)
4.Яка з наведених точок належить координатній площині yz?
A. A(0;3;1) Б. В(2;0;0)
В.(1;1;6)
Г. D(5;-3;-3)
В
Б
Б
А

50. Тестові завдання Скалярний добуток

a
1. Знайти скалярний добуток векторів
А. 0
Б. 12
В. 10
Г. -6
(1;-2;4), b (2;-3;1)
2. Ребро правильного тетраедра DABC дорівнює 2. Чому дорівнює
скалярний добуток векторів DA і DB ?
А. 0
Б. 1
В. 4
Г. 2
3.Чому дорівнює кут між векторами
А. 45o
Б. 60o
В. 120o
a (-1;0;1) і b (-1;1;0) ?
Г. 135o
4. Який наведених векторів перпендикулярний вектору a (-1;1;-1) ?
А. k (0;-1;1)
Б
Б. i (2;1;-1)
Г
m
В. (1;-1;1)
Б
Б
n
Г. (1;0;1)

51.

52.

Використана література
1. Геометрія 11- підручник (Г.В.Апостолова)
2. Геометрія 11- підручник (Г.П.Бевз)
3. Геометрія – 10 плани-конспекти уроків (О.М. Роганін)
4. Всі уроки геометрії 11 книга для вчителя( С.Бабенко)
5. Геометрія в таблицях (Є.П.Нелін)
6. Геометрія у визначеннях, таблицях і схемах 7-11
(В.А.Дергачов)