Применение тригонометрических формул для решения уравнений (часть 1)

1.

НОЧУ «Британская международная школа»
Применение
тригонометрических
формул для решения
уравнений
Часть I
Пестова Ю.В.

2.

Решим уравнение:
sin2x – cosx = 0
2sinxcosx – cosx = 0
cosx (2sinx – 1) = 0
cosx = 0,
sinx = ½;…
Найдите x
sin2x = 2sinxcosx

3.

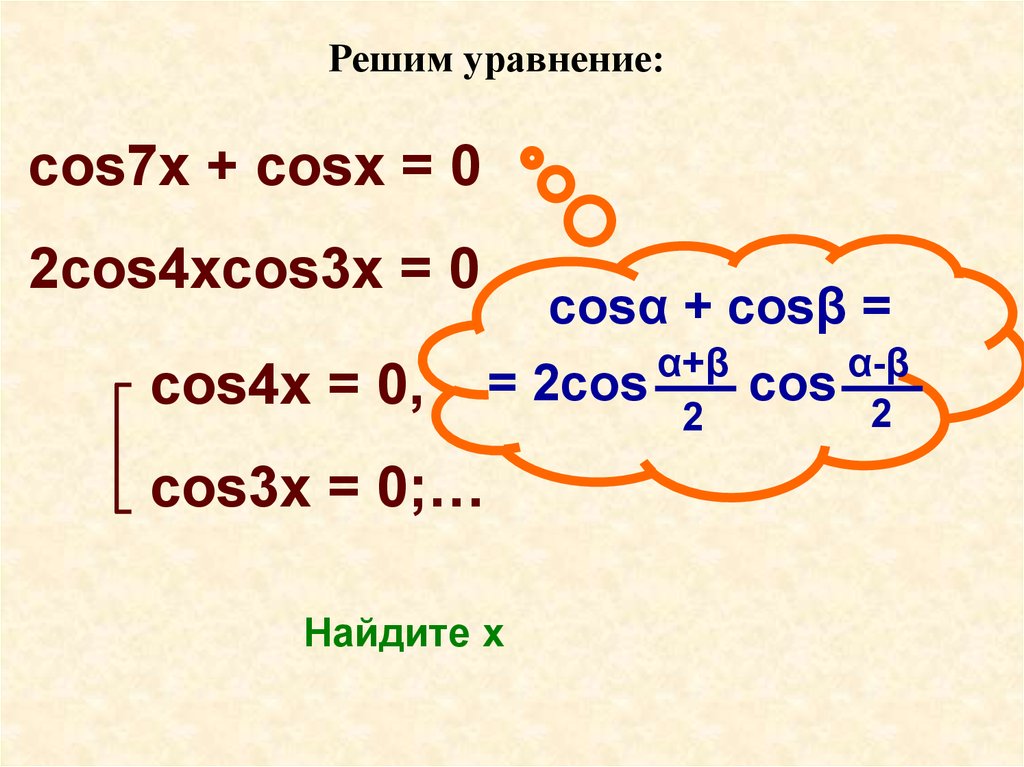
Решим уравнение:
cos7x + cosx = 0
2cos4xcos3x = 0
cos4x = 0,
cosα + cosβ =
=
cos3x = 0;…
Найдите x
α+β
2cos
2
α-β
cos
2

4.

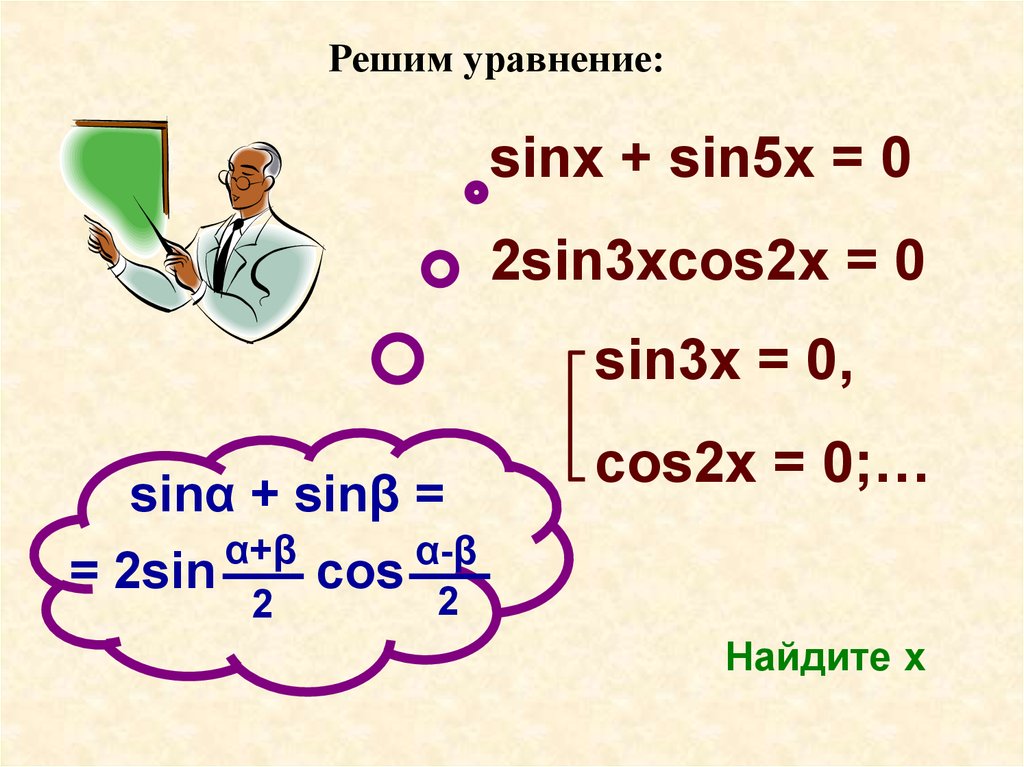
Решим уравнение:
sinx + sin5x = 0
2sin3xcos2x = 0
sin3x = 0,
sinα + sinβ =
α+β
α-β
= 2sin
cos
2
cos2x = 0;…
2
Найдите x

5.

Решим уравнение:
√2
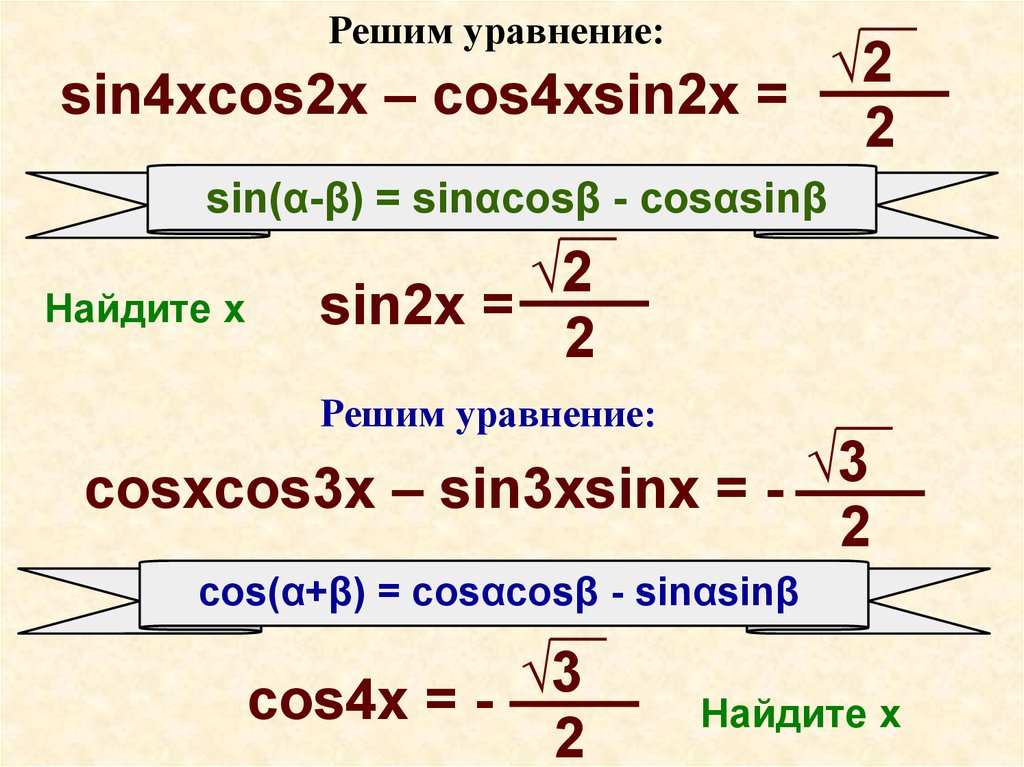
sin4xcos2x – cos4xsin2x =
2
sin(α-β) = sinαcosβ - cosαsinβ
Найдите x
√2
sin2x =
2
Решим уравнение:
√3
cosxcos3x – sin3xsinx = 2
cos(α+β) = cosαcosβ - sinαsinβ
√3
cos4x = 2
Найдите x

6.

Решим уравнение:
sin23x + cox23x + sin3x = 2
sin2x + cos2x = 1
1 + sin3x = 2
1
=
5
cos2x
sin3x = 1
Найдите x
1+
Решим уравнение:
tg2x
1
=
cos2x
tg2x = 4
tgx = ±2
Найдите x

7.

Решим уравнение:
√2
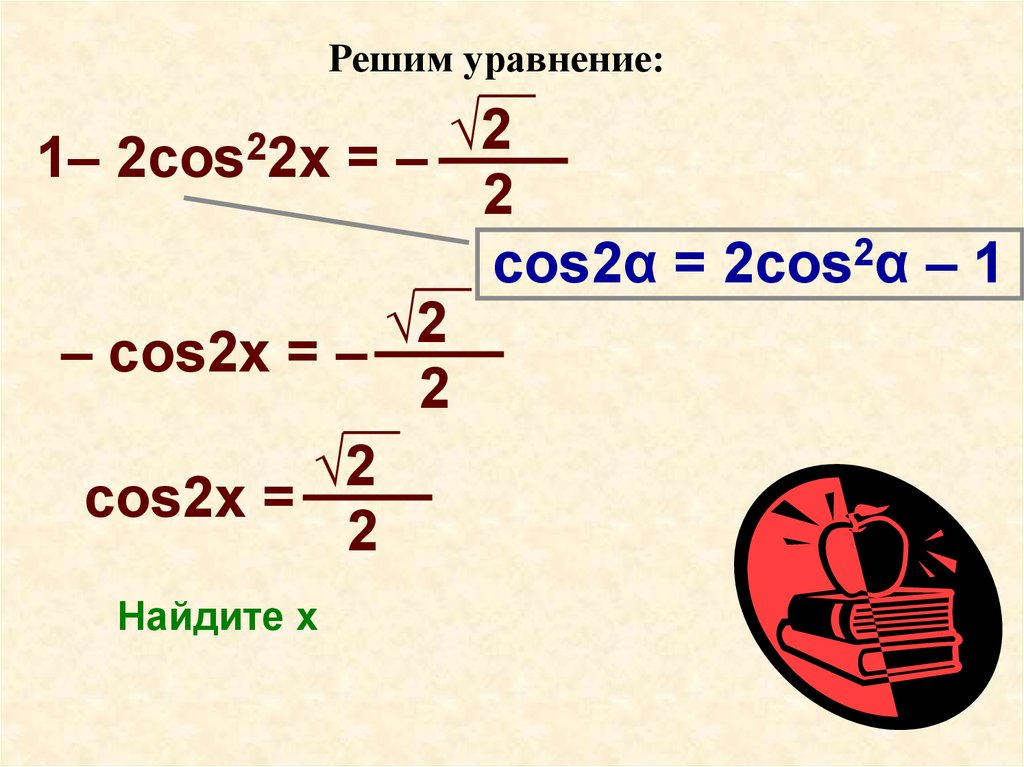
1–
=–
2
cos2α = 2cos2α – 1
√2
– cos2x = –
2
√2
cos2x =
2
2cos22x
Найдите x

8.

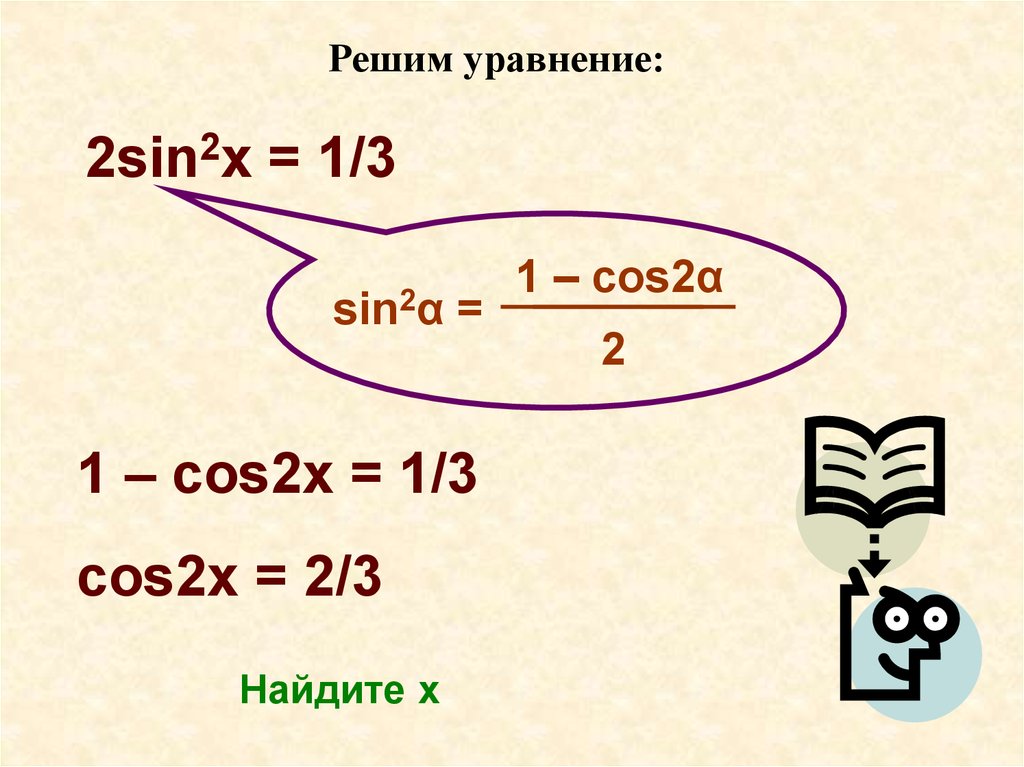
Решим уравнение:
2sin2x = 1/3
sin2α
=
1 – cos2x = 1/3
cos2x = 2/3
Найдите x
1 – cos2α
2