Similar presentations:
Степень с рациональным показателем. Степенная функция
1. Степень с рациональным показателем. Степенная функция.
2. Цели урока:
обобщить и систематизировать знанияпо данной теме;
проверить умения применять свойства
степеней с рациональным показателем
на практике;
развитие мыслительной деятельности –
умения анализировать, обобщать;
формирование интереса к предмету;
3. Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь.
Ломоносов М. В.4. Кодификатор требований к уровню подготовки выпускников по математике демоверсии 2010г.
5. Требования к уровню подготовки выпускников по математике демоверсии 2010 г. по теме «Степень с рациональным показателем.
Находить значение степени с рациональнымпоказателем;
проводить по известным формулам и правилам
преобразования буквенных выражений,
включая степени;
строить графики изученных функций;
находить производные элементарных функций;
исследовать в простейших случаях функции на
монотонность, находить наибольшее и
наименьшее значения функций.
6. Определение степени с рациональным показателем
Если- обыкновенная
Если
дробь (q ≠ 1) и a ≥ 0,то
под
т.е.
понимают
,
- обыкновенная
дробь (q ≠ 1) и a > 0,то
под
понимают
=
=
:
7. Вычислите:
а)д)
б)
е)
в)
ж)
г)
з)
:
8. Свойства степени
Если а>0, b>0, s и t – произвольныерациональные числа, то:
9. Назовите корень уравнения:
а) х⁶ = 729;б)
= 5;
в) 2х³ + 5 = 49;
г)
д)
= 3;
= 3.
10. Теорема
Если х > 0 и r – любое рациональноечисло, то производная степенной
функции y=
вычисляется по
формуле:
11. Найдите производную функции:
а)б)
у=
х⁶ ;
у=
в) у =
;
;
г) у = х² ·
.
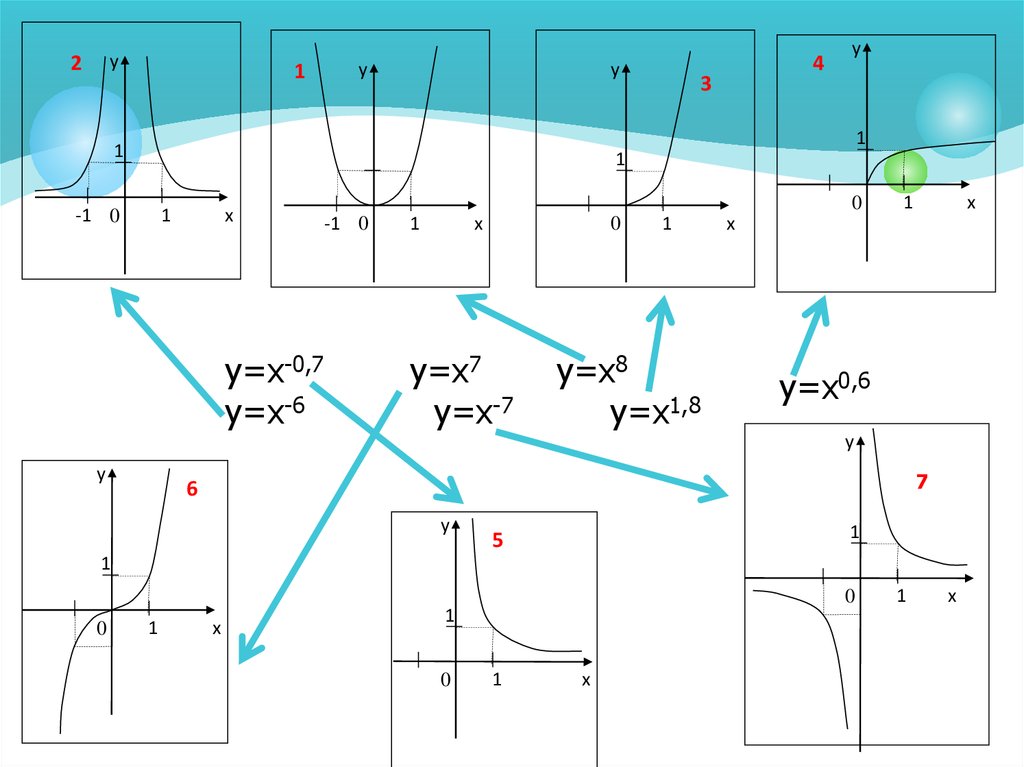
12.
у2
1
у
у
4
3
у
1
1
1
-1 0
1
х
у=х-0,7
у=х-6
0
-1 0
1
х
0
у=х7
у=х-7
1
у=х8
у=х1,8
1
х
х
у=х0,6
у
у
7
6
у
1
5
1
0
1
х
0
1
0
1
х
1
х
13. Группа А
1.Вычислите:5¹¹ ·
:
;
2.Найдите производную функции
у=
в точке х₀ = 16.
14. Группы В и С
1.Решить уравнение:x
x
2
sin cos 16 x 0 .
2
2
2. Найдите наименьшее значение
функции
на промежутке
.
(2х + 1)














 mathematics
mathematics








