Similar presentations:
Решение логарифмических неравенств
1. Решение логарифмических неравенств
(Рекомендации по выполнению задания С3).
2.
При решении логарифмических неравенствможно использовать условия
равносильности. Преимущество
использования условий равносильности по
сравнению с обычным способом решения
состоит в том, что не надо думать о том,
большим или меньшим единицы является
основание. Это особенно важно при
решении заданий ЕГЭ, когда время для их
решения ограничено.
3. Для неравенств вида loga f(x)> 0(< 0); loga f(x) ≥ 0 (≤ 0) существует
Для неравенств видаloga f(x)> 0(< 0);
loga f(x) ≥ 0 (≤ 0)
существует
Правило 1: Знак loga f(x) совпадает со
знаком произведения
(a 1)( f ( x ) 1)
в ОДЗ.
4.
Используя это правило, можно записатьусловие равносильности, включающее
ОДЗ
•для строгих логарифмических
неравенств:
f ( x ) 0,
loga f(x)> 0(< 0)
(a 1)( f ( x ) 1) 0( 0).
5.
•для нестрогих логарифмическихнеравенств:
f ( x ) 0,
log a f(x) 0 ( 0)
(a 1)( f ( x ) 1) 0( 0).
6.
Для логарифмических неравенств видаloga f(x) > loga g(x) и более сложных
существует
Правило 2. Знак
loga f (x ) - loga g (x )
разности
совпадает со
знаком произведения (a 1)( f ( x ) g ( x ))
в ОДЗ.
7.
Используя Правило 2, можно записатьусловие равносильности, включающее
ОДЗ для неравенств вида:
f(x) 0,
log a f(x) > (<) log a g(x) g ( x ) 0,
( a 1)( f ( x ) g ( x )) 0( 0).
8.
Также можно очень просто решитьболее сложные неравенства, используя
Правило 2, например:
log a f ( x ) log a g ( x )
(a 1)( f ( x ) g ( x ))
0( 0)
) 0( 0)
h( x )
h( x )
в ОДЗ.
9.
Очень важно, что освобождение отвсех логарифмов происходит за один
шаг. Использование данных правил
сводит решение логарифмических
неравенств к рациональным (дробнорациональным) неравенствам,
которые решаются методом
интервалов.
10. Рассмотрим применение Правила 1 на примере.
Решим логарифмическое неравенство:11.
4log 3 ( x )
5
7
log 7 ( x 2 x )
16
2
0
12.
Найдем ОДЗ:4
x ,
5
4
4
x 5 0,
x 5 ,
1
x ,
4
x 2 2 x 7 0; ( x 7 )( x 1 ) 0;
7
16
4
4
x
.
4
Применяя метод интервалов, найдем общее
решение данной системы:
4 1
7
(
; ) ( ; )
5 4
4
13.
По Правилу 1знак
4
log 3 ( x )
5
4
совпадает со знаком произведения (3 1)( x 1)
5
а знак
со знаком
7
log 7 ( x 2 x )
16
2
7
(7 1)( x 2 x 1)
16
2
Поэтому в ОДЗ имеем:
14.
4log 3 ( x )
5
7
log 7 ( x 2 x )
16
2
1
x
5
0
4
(3 1)( x 1)
5
0;
7
2
(7 1)( x 2 x 1)
16
1
x
5
0;
0
9
1
9
2
x 2x
( x )( x )
16
4
4
15.
Применяя метод интервалов, получим решениеданного неравенства:
1
1 9
( ; ) ( ; )
4
5 4
Найдем общее решение исходного неравенства с
учетом ОДЗ.
Ответ:
4
1
1 1
7 9
( ; ) ( ; ) ( ; )
5
4
5 4
4 4
16.
Таким образом,использование данных
правил, позволяет
просто справиться с
логарифмическими
неравенствами,
решение которых
обычным способом
потребует гораздо
больше вычислений.










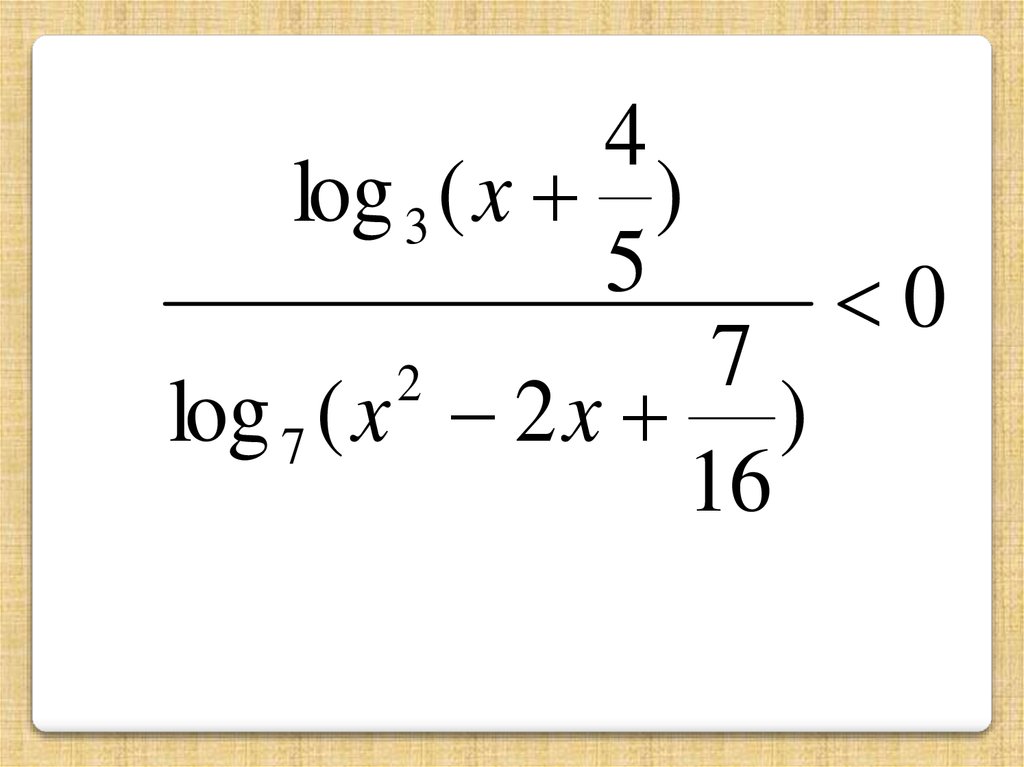






 mathematics
mathematics








