Similar presentations:
Решение логарифмических неравенств
1.
Решениелогарифмических
неравенств
11
2.
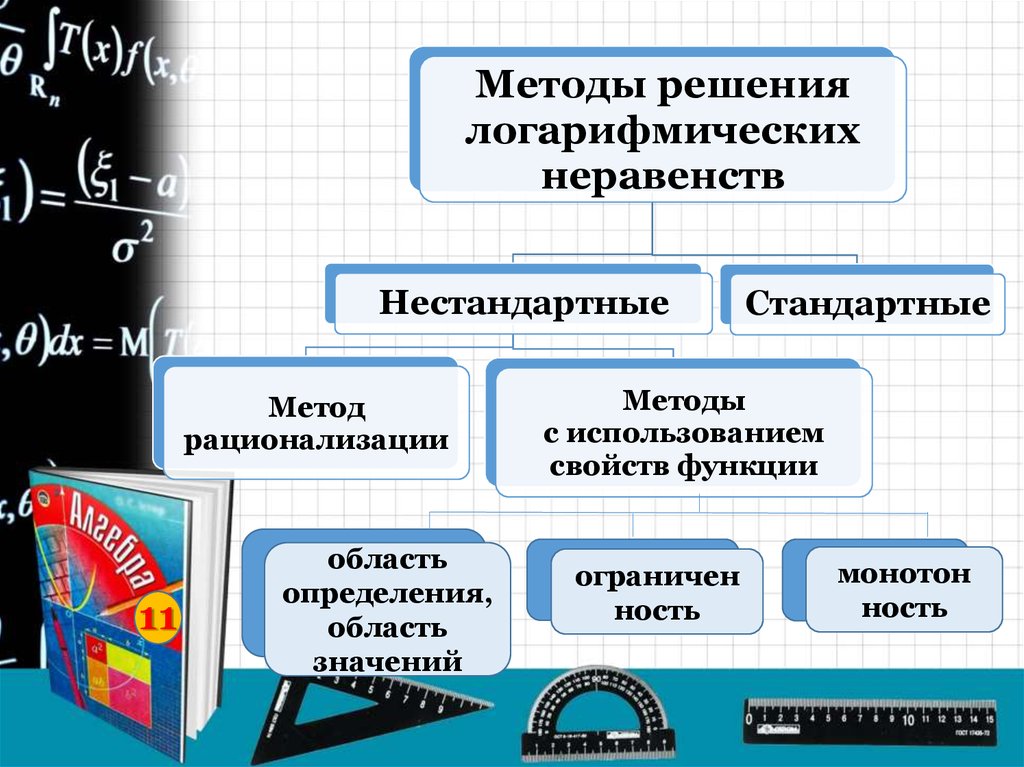
Методы решениялогарифмических
неравенств
Нестандартные
Метод
рационализации
11
область
определения,
область
значений
Стандартные
Методы
с использованием
свойств функции
ограничен
ность
монотон
ность
3.
Метод рационализацииСуть метода рационализации для решения
логарифмических неравенств (метода замены
множителя) состоит в том, что в ходе решения
осуществляется переход от неравенства,
содержащего логарифмические выражения,
к равносильному рациональному неравенству
(или равносильной системе рациональных
неравенств)
4.
Рассмотрим неравенства:loga f ( x) 0;
число
loga f ( x) loga g ( x) 0;
log a ( x ) f ( x) 0;
log a ( x ) f ( x) log a ( x ) g ( x) 0
функция
5.
1) loga f ( x) 0, a 0, a 1.log a f ( x) log a 1.
Если а 1, то f ( x) 1, значит,
log a t возрастает на R
(a 1) ( f ( x) 1) 0; Знак
Имеем
: a 1 0; f ( x) 1 0.
«сохраняется».
Если 0 a 1, то 0 f ( x) 1, значит,
(a 1) ( f ( x) 1) 0. log a t убывает на R
Следовательно :
Имеем : a 1 0; f(x) 1 0.
(a 1) ( f ( x) 1) 0,
log a f ( x) 0
f ( x) 0.
6.
loga f ( x) loga g ( x) 0, a 0, a 1.loga f ( x) loga g ( x),
Если a 1, то f ( x) g ( x) 0, тогда
(a 1)( f ( x) g ( x)) 0,
Знак
Если 0 a 1, то 0 f ( x) g ( x), значит,
«сохраняется».
(a 1)( f ( x) g ( x)) 0.
log a f ( x) log a g ( x) 0
Имеем :
(a 1)( f ( x) g ( x)) 0,
f ( x) 0,
g ( x ) 0.
7.
(a 1) ( f ( x) 1)loga f ( x) 0;
loga f ( x) 0;
(a 1)( f ( x) g ( x))
loga f ( x) loga g ( x) 0;
loga f ( x) loga g ( x) 0;
При решении учитываем ОДЗ!
8.
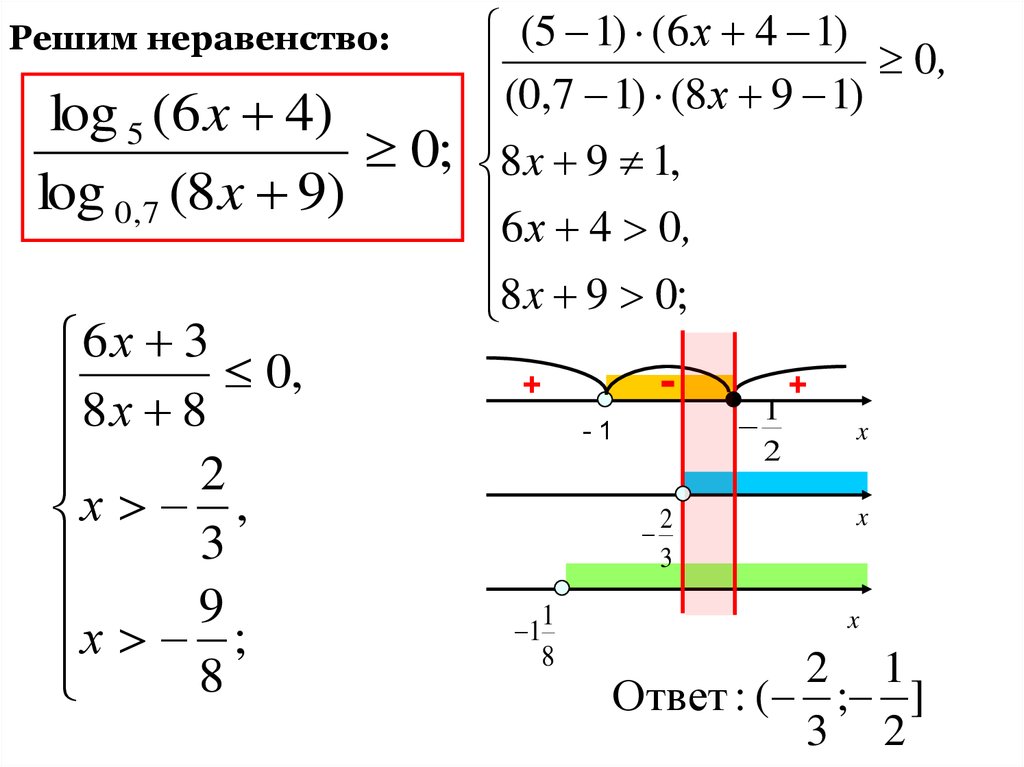
Решим неравенство:log 5 (6 x 4)
0;
log 0,7 (8 x 9)
6х 3
8 х 8 0,
2
х ,
3
9
х 8 ;
(5 1) (6 х 4 1)
(0,7 1) (8 х 9 1) 0,
8 x 9 1,
6 х 4 0,
8 x 9 0;
-
+
-1
1
1
8
2
3
1
2
+
x
x
x
2 1
Ответ : ( ; ]
3 2
9.
log a ( x ) f ( x) 0.Если a( x) 1, то f ( x) 1,
тогда (a( x) 1) ( f ( x) 1) 0.
Если 0 a( x) 1, то 0 f ( x) 1,
тогда (a( x) 1) ( f ( x) 1) 0;
log a(x) f(x) 0
Имеем:
(а( х) 1) (
a( x) 0,
a( x) 1,
f ( x) 0;
f ( x) 1) 0,
10.
log a ( x ) f ( x) log a ( x ) g ( x) 0,log a ( x ) f ( x) log a ( x ) g ( x)
Если a( x) 1, то f ( x) g ( x) 0,
тогда (a( x) 1) ( f ( x) g ( x)) 0.
Если 0 a( x) 1, то 0 f ( x) g ( x),
тогда (a( x) 1) ( f ( x) g ( x)) 0;
log a ( x ) f ( x ) log a ( x ) g ( x ) 0
Имеем:
( a ( x ) 1)( f ( x ) g ( x )) 0,
a ( x ) 0,
a ( x ) 1,
f ( x) 0,
g ( x ) 0.
11.
Решим неравенство:ОДЗ:
2 х 3 0,
2 х 3 1,
x 2 0;
log 2 x 3 x 1;
2
log 2 x 3 x 1
2
3
х 2 ,
х 1,
x 0.
log 2 x 3 x 1 0;
2
log 2 x 3 x log 2 x 3 (2 x 3) 0;
2
12.
log 2 x 3 x log 2 x 3 (2 x 3) 0;2
-1
(2 x 3 1) ( x
х 3 ;
2
х 1;
x 0;
2
2 x 3) 0,
(2 x 2)( х 1)( x 3) 0,
3
х ;
2
х 1;
x 0.
13.
2( x 1)( х 1)( x 3) 0,3
х ;
2
х 1;
x 0.
-1
-
+
3
( x 1) 2 ( x 3) 0,
х 3 ;
3
-1 0
2
2
х 1;
3
x 0. Ответ : ( 2 ; 1) ( 1;0) (0;3).
х
х
14.
x 21;
2x 1
4
Решим неравенство:
log 2 x 1
ОДЗ:
х 2
0,
2
x
1
2 х 1 0,
2 x 1 1;
4
1
x
,
2
1
х ,
2
x 1;
1
х ,
2
x 1;
15.
x 21;
2x 1
4
log 2 x 1
x 2
log 2 x 1 (2 x 1) 0;
2x 1
4
log 2 x 1
-1
x 2
2 x 1 1
(2 x 1) 0;
2x 1
4
2
x 2 4x 1
0;
2 x 2
2x 1
4
2
x 4x 3
0;
x 1
2x 1
4
16.
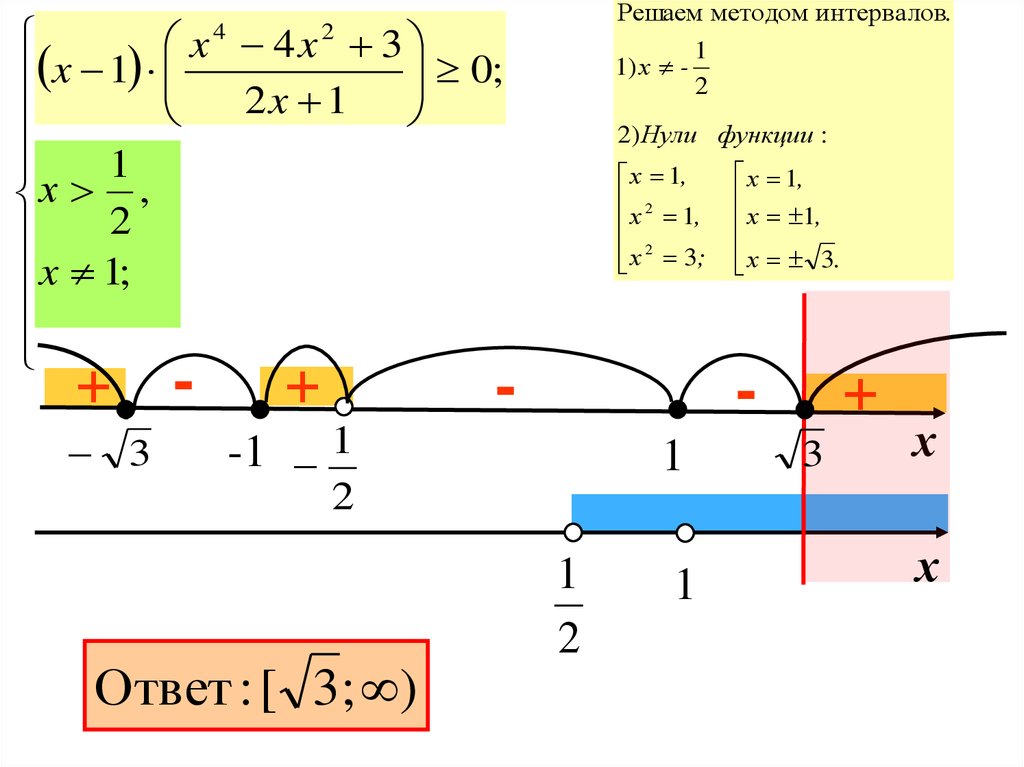
Решаем методом интервалов.x 4x 3
0;
x 1
2x 1
1
х ,
2
x 1;
4
+
3
-
2
+
1) х -
1
2
2) Нули функции :
х 1,
2
х 1,
х 2 3;
-
х 1,
х 1,
х 3.
+
-
-1 1
1
3
х
2
Ответ : [ 3; )
1
2
1
х
17.
Решить неравенство :log
1
49
(26 5 x) log 6 x
1
1
7
ОДЗ:
26
х
,
26 5 х 0,
5
6 x 0, x 6,
6 x 1; x 5;
26
,
х
5
x 5.
18.
log 1 (26 5 x) log 6 x49
1
1;
7
1
log 7 2 (26 5x) log 6 x 7 1;
1
log 7 (26 5 x) ( log 6 x 7) 1, ;
2
2 log (6 x)
log 7 (26 5x)
1
1 0;
2
log 7 (6 x)
log 7 (26 5 x) 2 log 7 (6 x)
0;
2 log 7 (6 x)
7
log 7 (26 5 x) log 7 (6 x)
0;
2 log 7 (6 x)
2
19.
log 7 (26 5 x) log 7 (6 x)0,
2 log 7 (6 x)
2
26 5 x (6 x) 2
0,
6 x 1
7-1>0
26 5 x 36 12 x x
0,
5 x
2
x 7 x 10
0,
x 5
2
( x 2)( x 5)
0,
x 5
20.
( x 2)( x 5)0
,
x 5
ОДЗ
26
,
х
5
x 5.
2
+
+
5
x
5 26
x
5
26
Ответ : 2;5 5; .
5
21.
Решите неравенства:1) log x 2 x 1 1;
2
6 x
2) log 0 ,25 x 2
1;
4
1
3) log 3 x
log 3 27 x 9 0;
27
4
x
3 x
4) log x 5
3;
log x 5
x 3
x
2
x 1
7 x
5) log x 8
;
1 log x 8
x 7
x 1
6) log 6 x
x4
0;
2
x 12 x 36
Практикум
22.
log x 2 x 1 1;2
x 1 x 1 x 2 0,
х 0,
x 1,
x 1 .
2
2
1
Ответ : - 1;0 0; 1; .
2
23.
6 xlog 0 ,25 x 2
1
4
2
6
х
x
2
(
0
,
25
x
1) (
) 0,
4
x 6,
х 0,
x 2,
x 2.
Ответ : - ; 3 - 2;0 0;2 2;6 .
24.
log 3 x1
log 3 27 x 9 0
27
3 log 3 x 3 2 log 3 3x 9 0,
х 0,
1
x ;
3
log 3 x 3 1 0,
х 0,
1
x ;
3
3x 1 3 3x 0,
х 0,
1
x ;
3
1
Ответ : 0; 1; .
3
25.
4x
3 x
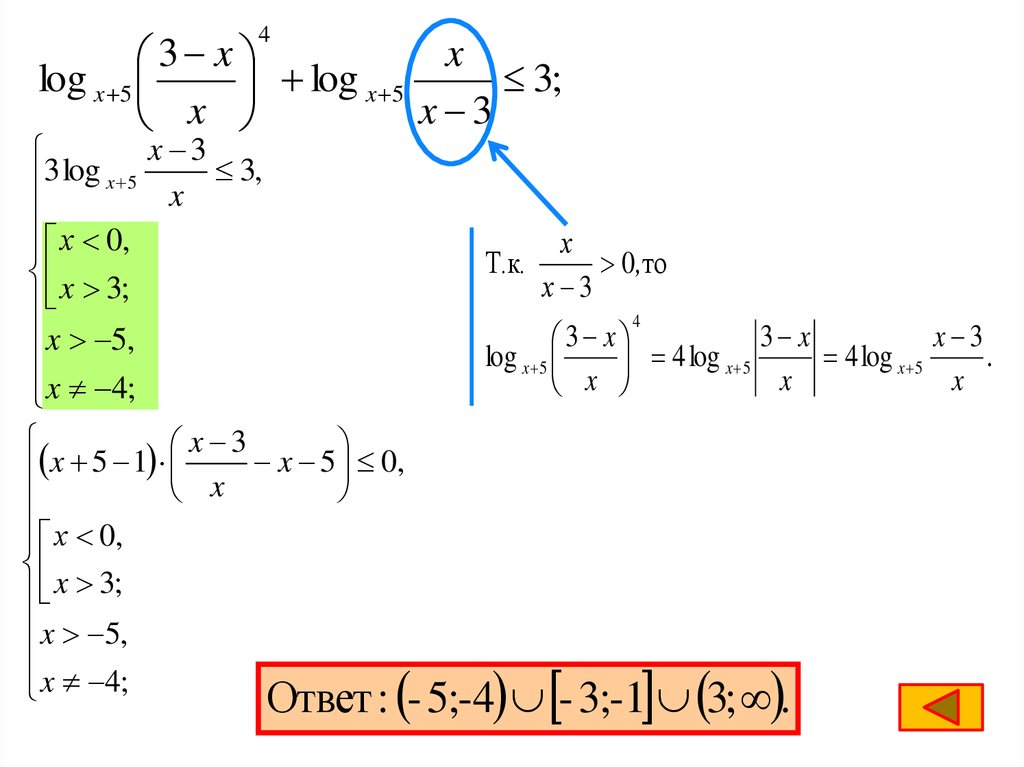
log x 5
3;
log x 5
x 3
x
x 3
3
log
3,
x 5
x
х
х 0,
Т.к.
0,то
x 3;
х 3
4
3
x
3 x
x 3
x 5,
log x 5
4 log x 5
.
4 log x 5
x
x
x
x 4;
x 3
x
5
1
x
5
0,
x
х 0,
x 3;
x 5,
x 4;
Ответ : - 5;-4 - 3;-1 3; .
26.
2x 1
7 x
log x 8
;
1 log x 8
x 7
x 1
x 7
x 7
2 log x 8
1 log x 8
;
x 1
x 1
x 7
log x 8
1 0;
x 1
x 2 8 х 15
0,
x 7
x 1
х 1,
x 7;
x 8,
Ответ : - 8;-7 - 5;-3 7; .
x 7;
27.
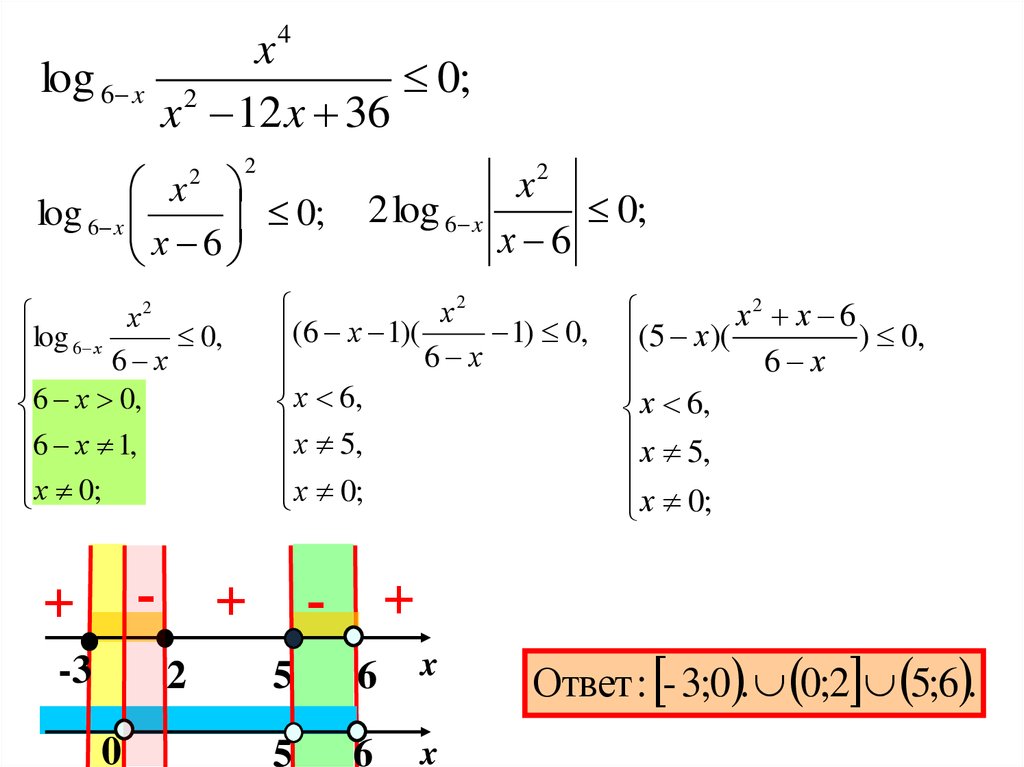
4log 6 x
x
0;
2
x 12 x 36
2
x
0;
log 6 x
х 6
2
х2
0,
log 6 х
6 х
6 х 0,
6 х 1,
х 0;
-
+
-3
0
х2
1) 0,
(6 х 1)(
6 х
х 6,
х 5,
х 0;
+
2
2 log 6 x
x2
0;
х 6
х2 х 6
) 0,
(5 х)(
6 х
х 6,
х 5,
х 0;
+
5
6
x
5
6
x
Ответ : - 3;0 . 0;2 5;6 .
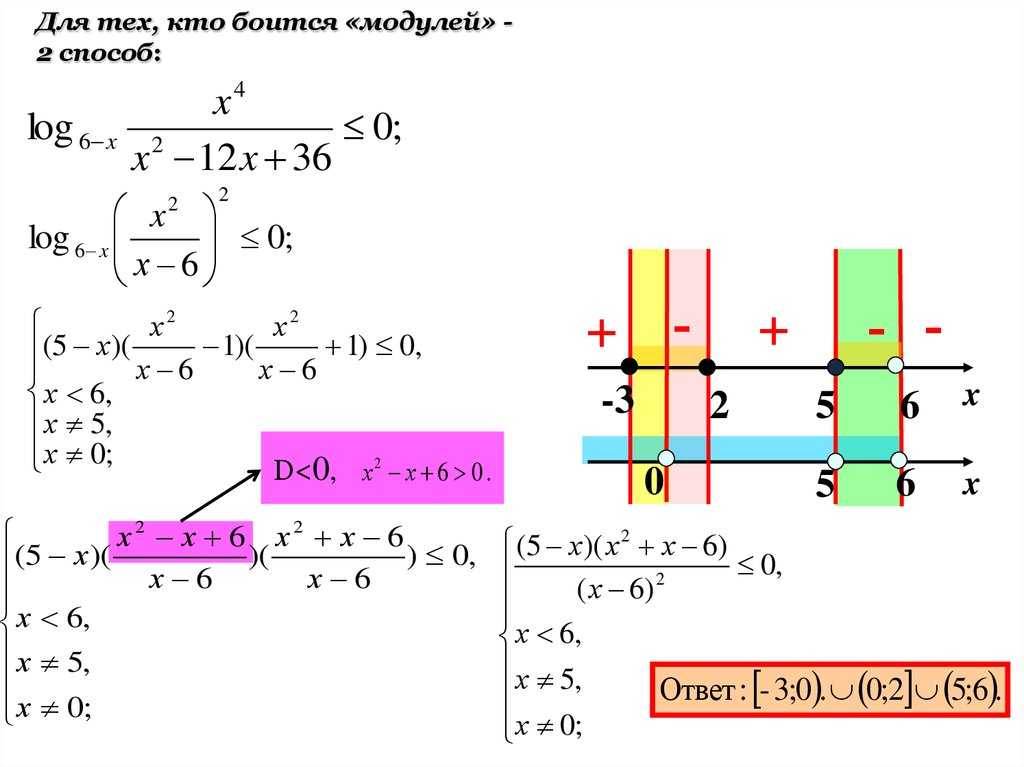
28.
Для тех, кто боится «модулей» 2 способ:log 6 x
x4
0;
2
x 12 x 36
2
x
0;
log 6 x
х 6
2
х2
х2
1)(
1) 0,
(5 х)(
х 6
х 6
х 6,
х 5,
х 0;
D<0, х 2 х 6 0 .
х2 х 6 х2 х 6
)(
) 0,
(5 х)(
х 6
х 6
х 6,
х 5,
х 0;
-
+
-3
2
0
- -
+
5
6
x
5
6
x
(5 х)( х 2 х 6)
0,
2
( х 6)
х 6,
х 5,
Ответ : - 3;0 . 0;2 5;6 .
х 0;
29.
Методы с использованиемсвойств функции
1) Использование неотрицательности
функций
11
30.
1131.
32.
Методы с использованиемсвойств функции
2) Метод мини-максов (метод оценки)
11
33.
34.
35.
Методы с использованиемсвойств функции
3) Использование монотонности функций
11









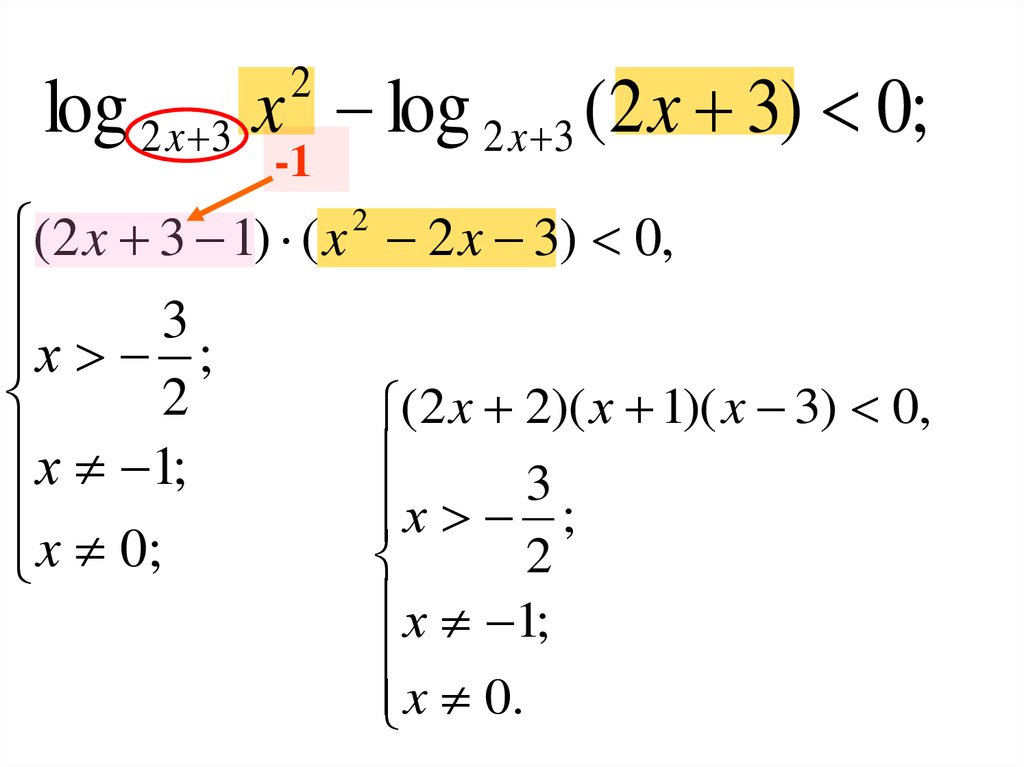


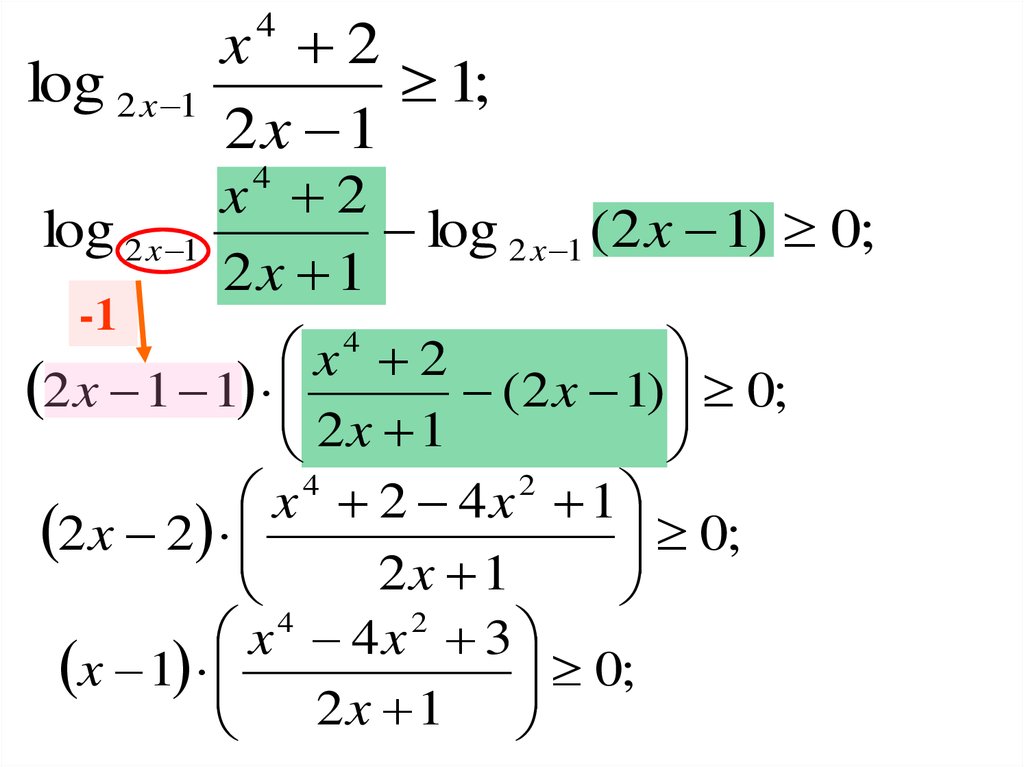


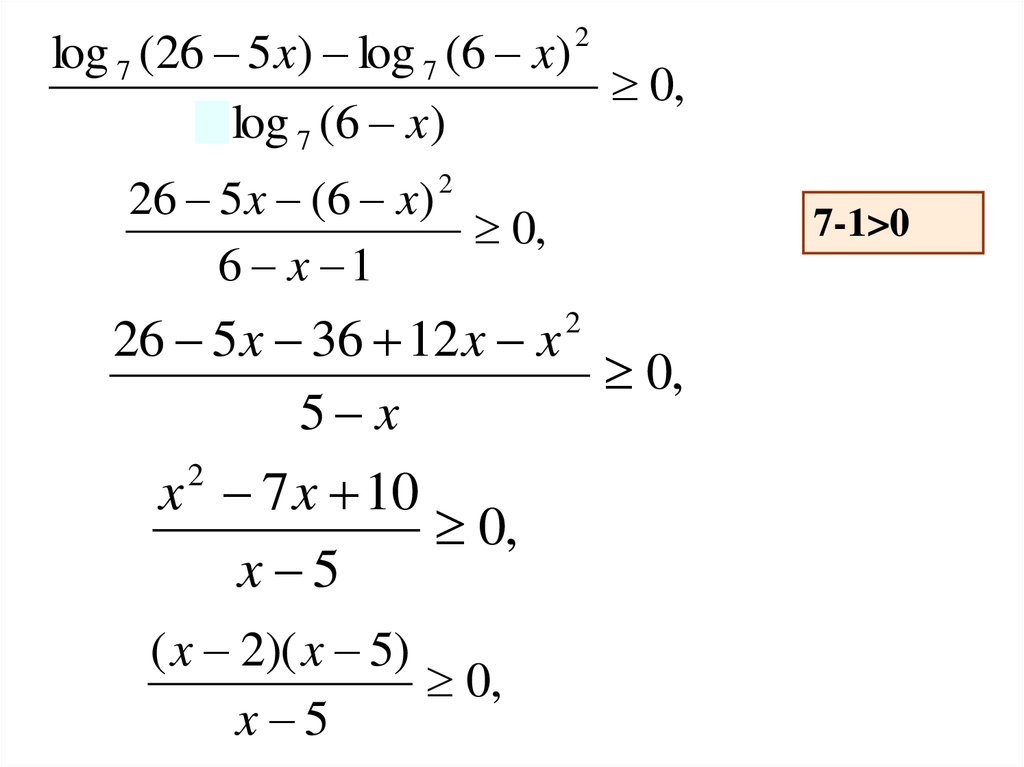
















 mathematics
mathematics