Логарифмические уравнения и неравенства

1. Понятие логарифма

Логарифмом положительного числа b по
положительному и отличному от 1
основанию а называют показатель
степени, в которую нужно возвести
число а, чтобы получить число b
logab = c, ac = b; а ≠ 1, a > 0, b > 0
a
logab
=b
- основное логарифмическое тождество

2. Примеры

1. log2 8 = 3, 23 = 8;
2. log3 729 = 6, 36 = 729;
3. log0,2 25 = -2, (0,2)-2 = 25;
4. log4 8 = 1,5, 41,5 = 8;
5. log2 2 = 1, 21 = 2;
6. log10 1 = 0, 100 = 1;
7. log49 1/7 = -0,5, 49-0,5 = 1/7;
8. log0,1 10000 = -4, 0,1-4 = 10000.

3. Основные свойства логарифмов

1. loga 1 = 0;
10. loga bm = m logab;
m
m
logab;
11. loga b =
k
logс b
;
12. loga b =
logс а
1
;
13. loga b =
logb а
14. loga b ∙ logc d =
2. loga a = 1;
1
3. loga a = -1;
1
;
4. logak a =
k
5. loga am = m;
m
m
6. logak a = ;
k
= logc b ∙ loga d
7. loga bc = logab + logac;
15. alog b = blog a
b
8. loga
= logab − logaс;
c
1
9. loga b = logab;
k
k
c
k
c

4. Логарифмические уравнения

Уравнения вида loga f(x) = logа h(х), где а ≠ 1, a > 0
называют логарифмическими уравнениями
⟺
loga f(x) = loga h(х)
f(x) = h(х)
f(x) > 0
h(х) > 0
Методы решения логарифмических уравнений:
1. Функционально-графический метод.
2. Метод потенцирования.
3. Метод введения новой переменной.

5. Логарифмические уравнения. Примеры

Пример 1
log3 x 2 3x 5 log3 7 2x
x 2 3x 5 7 2x
7 2x 0
x 2 x 12 0
x 3,5
x1 3
x 2 4
x 3,5
x 3
Ответ: -3.
Пример 2
log2 x 4 log2 2x 3 log2 1 2x
log2 x 4 2x 3 log2 1 2x
x 4 2x 3 1 2x
x 4 0
2x 3 0
1 2x 0
2x 2 13x 11 0
x 4
x 1,5
x 0,5
x 1 1
x 2 5,5
1,5 x 0,5
Ответ : 1.

6.

Логарифмические уравнения. Примеры
Пример 3
log x 4 x 2 1 log x 4 5 x
x 2 1 5 x ,
2
x 1 0,
5 x 0,
x 4 0,
x 4 1;
x 2 x 6 0,
x 1,
x 1;
4 x 5,
x 3;
x1 3
x 2 2
x 3
4 x 1,
1 x 5;
Ответ: 2.
x=2

7.

Логарифмические уравнения. Примеры
Пример 4
7
x
lg
10
7
2
lg x lg x 1
lg x 1
lg 2 x lg x 1
x
lg x lg 10 lg x 1,
10
где x 0, x 10
lg
пусть lg x t , где t 1, тогда
7
t t 1
t 1
t 1 t 2 t 1 7
2
Вернемся к исходной переменной
t3 1 7
lg x 2
t3 8
x 102
t 2
x 100
Ответ: 100.

8. Логарифмические неравенства

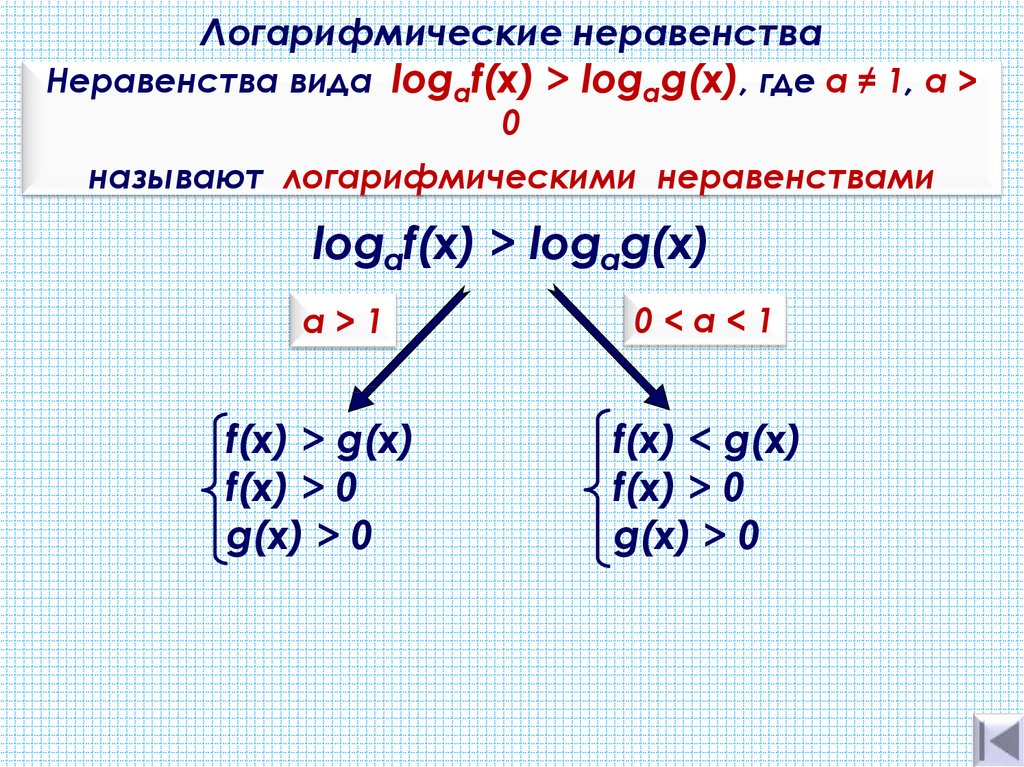
Неравенства вида logaf(x) > logаg(х), где а ≠ 1, a >
0
называют логарифмическими неравенствами
logaf(x) > logаg(х)
а>1
f(x) > g(х)
f(x) > 0
g(x) > 0
0<а<1
f(x) < g(х)
f(x) > 0
g(x) > 0

9. Логарифмические неравенства. Примеры

Пример 1
log3 2x 4 log3 14 x
Пример 2
log 1 16 4x x 2 4
2
т.к . а 3 1, то
log 1 16 4x x 2
2x 4 14 x ,
2x 4 0,
14 x 0;
2
4
log 1 16 4x x 2 log 1 16
2
2
1
1, то
2
16 4x x 2 16,
16 4x x 2 0; лишнее условие
4x x 2 0
x 2 4х 0
т.к . а
3x 18,
x 2,
x 14;
x 6,
x 2,
x 14;
x x 4 0
2
1
log 1
2 2
6
Ответ: (6; 14).
14
х
+
0
−
Ответ: [0; 4].
4
+
х

10.

Логарифмические неравенства. Примеры
Пример 3
lg x lg 45 x 2 lg 2
lg x 45 x lg100 lg 2
lg 45x x 2 lg 200
т.к . а 10 1, то
45x x 200,
45 x 0,
x 0;
2
Пример 4
log22 x 2 5log2 x 1 0 ОДЗ : x 0
2log x
2
2
2
2
5 log2 x 1 0
4log x 5log2 x 1 0
пусть log 2 x t , тогда
4t 2 5t 1 0
н .ф. : 4t 2 5t 1 0
1
t
1 4,
+
+
−
2
x 45x 200 0,
t 2 1;
t
1
1
2
x 45, н .ф. : х 45х 200 0 1
4
t
1
x 0;
х1 5,
4
х 40;
Вернемся к исходной переменной
2
+
−
+
1
х
log 2 x 1, т.к . а 2, то
0 5
40 45
4
4
Ответ: (0; 5) ∪ (40; 45).
2 х 2
Ответ : [4 2 ; 2].

11.

Логарифмические неравенства. Примеры
Пример 5
logx 2 2x 3 logx 2 24 6x
Возможны два случая :
x 2 1,
2x 3 24 6x ,
1
2x 3 0,
24 6x 0;
x 3,
x 27 ,
8
x 1,5,
x 4;
1,5 3 3,375 4
x ∈ (3,375; 4)
0 x 2 1,
2x 3 24 6x ,
2
2x 3 0,
24 6x 0;
2 x 3,
x 27 ,
8
x 1,5,
x 4;
х
1,5 2 3
Ответ: (2; 3)∪(3,375; 4) .
х
3,375 4
x ∈ (2; 3)