Логарифмические неравенства и методы их решения

1. Логарифмические неравенства и методы их решения

2. Логарифмические неравенства

Определение: неравенства, содержащие
неизвестное под знаком логарифма (и) или в
основании логарифма называются
логарифмическими.

3. Простейшее логарифмическое неравенство имеет вид

log a x b
Знак неравенства может быть любым ( , , ), где
a > 0, a ≠ 1

4. Решение логарифмических неравенств основано на строгой монотонности логарифмической функции. Известно, что

1. При основании, большем единицы,
логарифмическая функция возрастает;
2. При
положительном
основании,
меньшем единицы, логарифмическая
функция убывает.

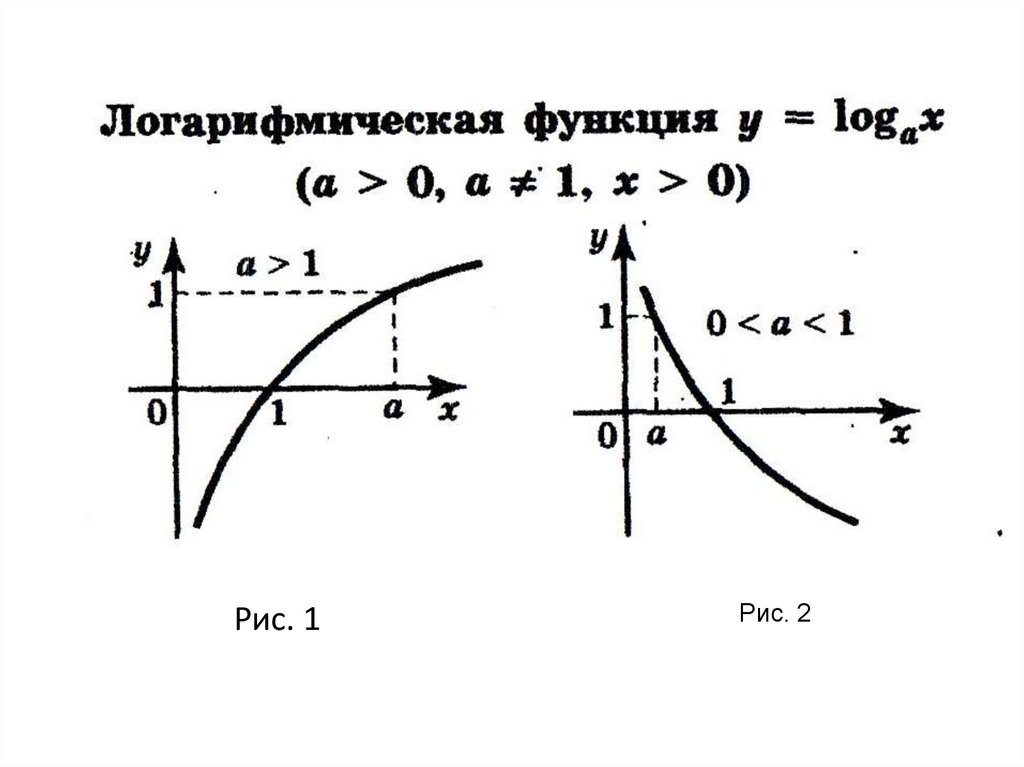
5.

Рис. 1
Рис. 2

6.

Логарифмическое неравенство вида
log a x b
(1)
эквивалентно следующим системам неравенств:
а 1
0 а 1

7.

Решить неравенство:
Решение:
Ответ:
log 2,5 x 2.
x 2,52 x 6,25
x 0
x 0
x 0; 6,25 .

8.

Логарифмическое неравенство вида
log a x b
(2)
эквивалентно следующим системам неравенств:
а 1
0 а 1

9.

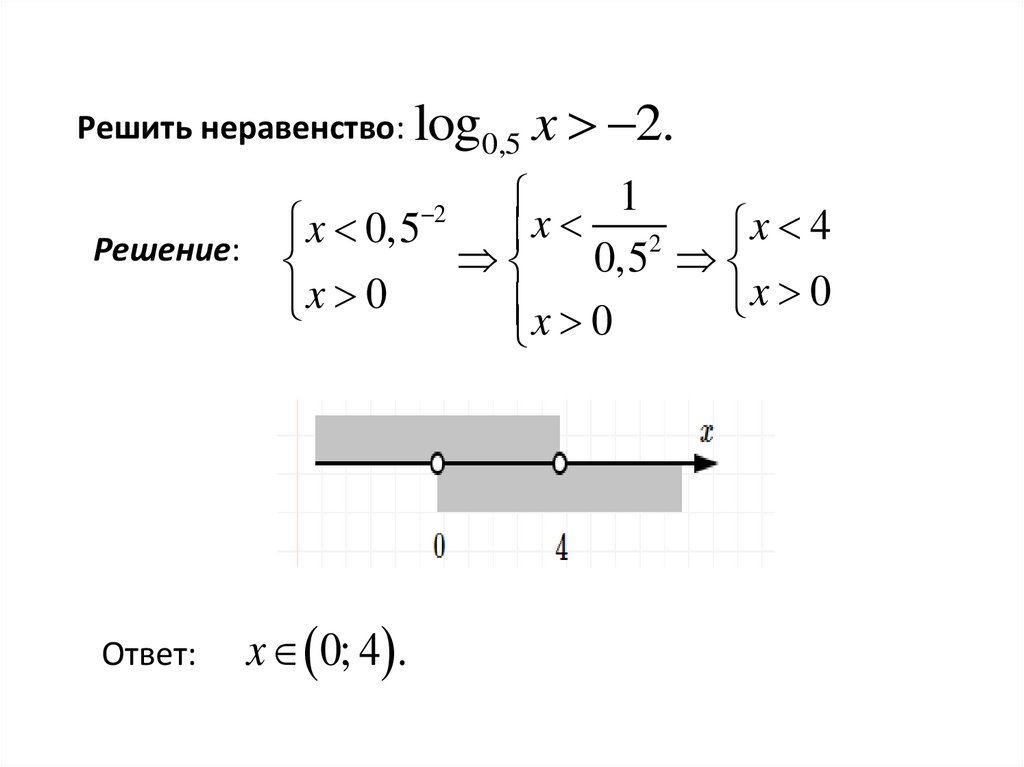
Решить неравенство: log0,5
x 2.
1
x
x
0,5
x 4
2
Решение:
0,5
x 0
x 0
x 0
2
Ответ:
x 0; 4 .

10. Методы решения логарифмических неравенств

1.
2.
3.
4.
Метод использования определения логарифма.
Метод потенцирования.
Метод введения новой переменной.
Графический метод.

11. 1. Метод использования определения логарифма

Логарифмическое неравенство вида
log a f ( x ) c
(3)
f ( x ) 0, a 0, a 1.
Равносильно системам неравенств:
а 1
0 а 1

12. Решить неравенство:

Решение:
Ответ:
log5 3x 1 2
2
x 8
3
x
1
5
3
x
25
1
1
3
x
1
0
3
x
1
x
3
x 8; .

13. Решить неравенство:

log 1 4 x 1 2
7
1
4
x
1
Решение:
7
4 x 1 0
Ответ:
x 12; .
2
x 12
4 x 1 7
1
x
4
x
1
4
2

14. 2. Метод потенцирования

Определение: под потенцированием
понимается переход от равенства,
содержащего логарифмы, к равенству, не
содержащему их.

15. Логарифмическое неравенство вида

loga f ( x ) loga g( x )
f ( x ) 0 , g( x ) 0 ,a 0 ,a 1.
Равносильно системе неравенств:
а 1
f (x) g(x),
g(x) 0
0 а 1
f (x) g(x),
f (x) 0
(5)

16. Решить неравенство:

lg
2 x 3 lg x 1
2 x 3 x 1 2 x x 1 3
x 4
Решение:
x 1 0
Ответ:
x 4; .
x 1
x 1

17. Логарифмическое неравенство вида

loga f ( x ) loga g( x )
f ( x ) 0 , g( x ) 0 ,a 0 ,a 1.
Равносильно системе неравенств:
а 1
f (x) g(x),
f (x) 0
0 а 1
f (x) g(x),
g(x) 0
(6)

18. Решить неравенство:

log0,5 4 x 7 log 0,5 x 2
4x 7 x 2
4 x x 2 7
x 3
Решение:
x 2 0
Ответ:
x 3; .
x 2
x 2

19.

3. Метод введения новой переменной
2
log
Решить неравенство:
2 x 4log 2 x 3

20. 4. Графический метод

В одной системе координат строят графики двух функций.
В зависимости от знака неравенства выбирается
интервал.

21. Решить неравенство:

log 2 x 6 x
Решение:
y log 2 x
y 6 x

22.

y log 2 x
y 6 x
Ответ:
x 0; 4

23. СПАСИБО ЗА ВНИМАНИЕ!