Similar presentations:
Повторение. Решение логарифмических уравнений
1. Тема урока: «Повторение. Решение логарифмических уравнений»
2.
Джон Непер (1550-1617)-шотландскийбарон, математик, один из
изобретателей логарифмов. В 1550-х
годах пришел к идее логарифмических
вычислений и составил первые
таблицы логарифмов, однако свой
знаменитый труд «Описание
удивительных таблиц логарифмов»
опубликовал лишь в 1614 году. Ему
принадлежит определение
логарифмов, объяснение их свойств,
таблицы логарифмов, синусов,
косинусов, тангенсов и приложения
логарифмов в сферической
тригонометрии.
3.
• Вы видите равенства, содержащиепеременную:
log 2 x 3
log 2 ( x 12) 2
lg( x 2) lg 2 x
1
log x
3
27
• Как называются эти равенства?
Что общего у них?
4. Понятие логарифма
Логарифмом положительного числа b поположительному и отличительному от 1
основанию a называют показатель степени, в
которую нужно возвести число а , чтобы
получить число b.
a
Пример:
loga b
b
log 2 8 3 , т.к. 23 =8
1
log 3 (
) 3, т.к. 3-3 =1/27
27
5. Вычислить : (устно)
1log 5
25
…
• log 416=…
• log 1 9 …
3
log 2=…
log6 1=…
log3 3=…
6.
• Десятичными называют логарифмыпо основанию 10 и обозначают lg.
Например:
lg 1000= 3
, т.к. 103 =1000
1
=-1
lg
10
, т.к.
10-1
1
=
10
7. Решить уравнение:
Log3 (2x-1) =3Решение:
О.Д.З.
2x-1>0
2x>1
x>1/2
2x-1=33
2x-1=28
2x=28
x=14
Ответ: x=14
Самостоятельно:
log2 (1-2x)=0
8.
Основные свойства логарифмовlog a 1 0
log
Например:
3
1 0
0
, т.к. 3 1
log6 1=0 , т.к. 60 =1
log 3 1 0
0
, т.к. 3 1
9.
log a a 1Например:
log5 5=1 , т.к. 51=5
10.
log a ( xy) log a x log a yНапример:
log 15 3+ log 15 5= log 15 (3*5) = log 15 15=1
11. Вычислить (устно):
log 12 4+ log 12 3=log 4 8+ log 4 2=
lg 25+ lg 4 =
12.
log 0,6 ( x 3) log 0,6 ( x 3) log 0,6 (2 x 1)13.
xlog ( ) log x log y,
a y
a
a
где y 0
Например:
15
log 5 15- log 5 3= log 5 ( 3 ) = log 5 5=1
14. Вычислить (устно):
log 2 15- log 2 30=log 28- log 7=
1
2
1
2
15. Решить уравнение:
log 7 4 log 7 x log 7 9О. Д .З.x 0
x
log 7 4 log 7 ( )
9
x
4 ; x 36
9
Ответ : х 36
Самостоятельно :
log 0, 4 9 log 0, 4 x log 0, 4 3
16. Вычислить (устно):
log a x p log a xp
Например: 2
2 log2 5
2
log2 52
Вычислить (устно):
8
2 log8 3
3
4 log3 2
25
17. Решить уравнение:
lg( 2 x) 2 lg 4 lg 2Каким методом решались эти уравнения?
18. Решить уравнение:
Какие ещё методы решения уравнения вызнаете?
log 2 x 4 log 2 x 3 0
2
19. Ответы к самостоятельной работе
III
a) x 8
a) х 6
б)x 0
б ) x 13
в) х 5
1
в ) х 4; x
8
20. Домашняя работа
Повторить§50,51
№1549, 1558 (г)









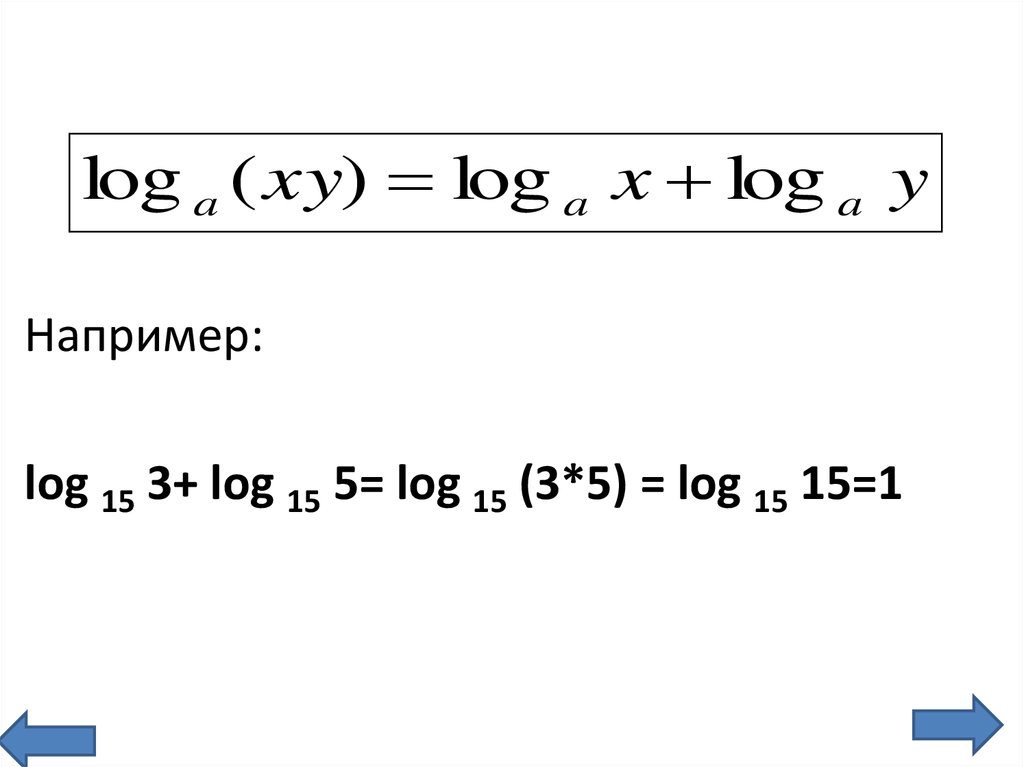










 mathematics
mathematics








