Similar presentations:
Решение логарифмических уравнений (10 класс)
1.
Решение логарифмическихуравнений
2.
loga b=Хх
а =b
3. Основное логарифмическое тождество:
aloga b
b
4.
log a a 1 log a 1 0log a a c
c
5. Свойства логарифмов:
a>0,b>0,c>0, c≠1,n≠1log c a log c b log c ( ab)
a
log c a log c b logc
b
n log c a log a
c
n
6. Перепишите равенства в виде логарифмических равенств:
Ответ :3
а)2 8
а)3 log 2 8
б )3 1
б )0 log 3 1
1
2
в )4
16
1
в) 2 log 4
16
0
7. Запишите числа в виде логарифмов с основанием 2:
Ответ:а) 4 = a )4 log 2 16
б) - 2 = б ) 2 log 1
2
4
в) 0 =
в
)
0
log
1
2
г) 1 =
г )1 log 2 2
8.
Вычислите:log 6 8 log 6 2 log 6 9
Ответ: 2
9.
Определение:Уравнение, содержащее
переменную под знаком
логарифма, называется
логарифмическим
log x b
a
a 0 , a 1
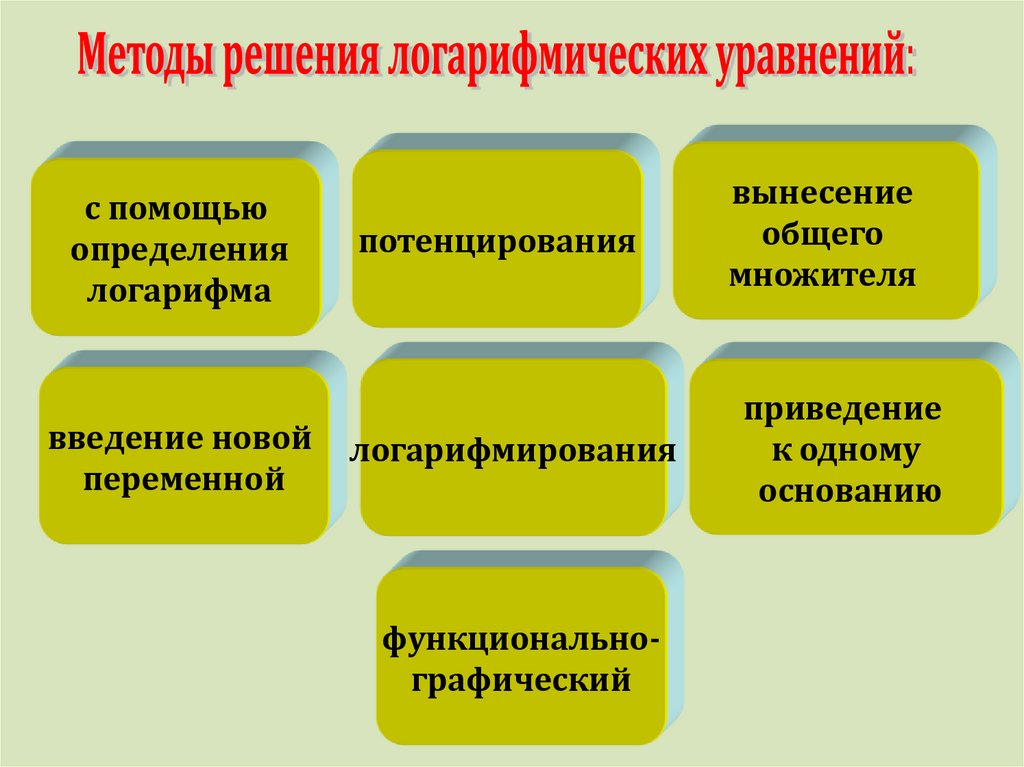
10.
Основные методы решениялогарифмических уравнений:
11.
с помощьюопределения
логарифма
введение новой
переменной
потенцирования
вынесение
общего
множителя
логарифмирования
приведение
к одному
основанию
функциональнографический
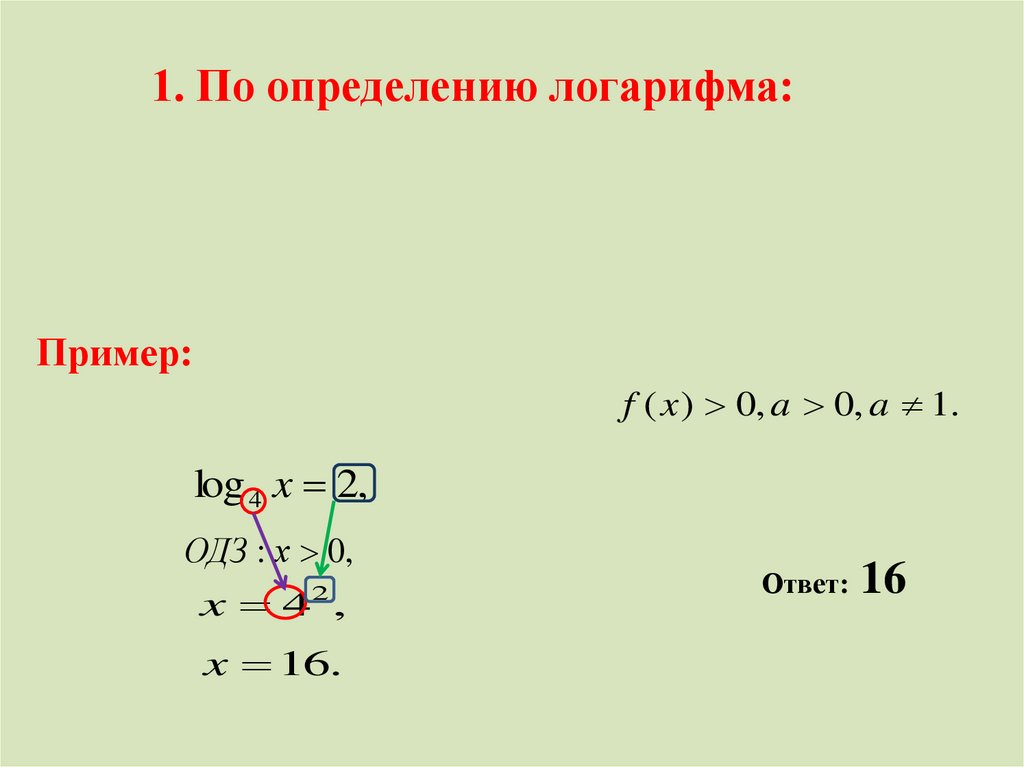
12.
1. По определению логарифма:Пример:
f ( x ) 0, a 0, a 1.
log 4 x 2,
ОДЗ : х 0,
x 4 ,
2
x 16.
Ответ: 16
13.
Пример :log 3 (2 x 1) 2,
2x 1 3 ,
2
2 x 1 9,
x 4.
Проверка:
log 3 (2 4 1) 2,
log 3 9 2,
2 2
Ответ: 4
14.
log 2 x 1Ответ: х=2
15. Решите логарифмические уравнения:
log x 5 2x 5
2
x 5 , т.к. 5 0
Ответ : x 5
log 4 x 0,5
0 .5
x 4
х 4
x 2
Ответ : x 2
16.
2. Метод потенцирования:Под потенцированием понимается переход от
равенства, содержащего логарифмы, к равенству,
не содержащему их:
если , loga f(х) = loga g(х),
то f(х) = g(х), f(х)>0, g(х)>0, а > 0, а≠ 1
Метод потенцирования применяется в том случае,
если все логарифмы, входящие в уравнение, имеют
одинаковое основание
17.
Пример:log 2 ( x 2 7 x 5) log 2 (4 x 1),
x 2 7 x 5 4 x 1,
x 2 3x 4 0,
x1 1, x2 4.
переходим от равенства, содержащего
логарифмы, к равенству,
не содержащему их
Проверка:
x 1 log 2 (12 7 1 5) log 2 (4 1 1) log 2 3 log 2 3 - верно
2
x 4 log 2 (( 4) 7 ( 4) 5) log 2 (4 ( 4) 1) log 2 ( 17) log 2 ( 17)
- не верно
Ответ: 1
18. решить
14
lg 2 x lg x 15
4
Ответ: корней нет
19. Решите уравнения потенцированием:
а) log2 (3x – 6) = log2 (2x – 3);20. Метод потенцирования:
Признак:1. Пропотенцировать обе
части уравнения по
уравнение должно
основанию равному
быть представлено в виде
основанию логарифма;
равенства двух логарифмов
2. Перейти к равенству
по одному основанию
подлогарифмических
выражений, применив
log a f x log a g x
свойство логарифма;
3. Решить уравнение и
проверить
полученные корни;
4. Записать
удовлетворяющие
корни в ответ.
21. 3. Метод вынесения общего множителя:
Стр.258, задача 522.
4. Метод введения новой переменной:Пример:
log 32 x log 3 x 2
ОДЗ:
Пусть
log 3 x t ,
x 0.
тогда
t 2 t 2,
t 2 t 2 0.
t1 1, t2 2.
Значит,
log 3 x 1
или
log 3 x 2
x 3 1
x 32
1
x .
3
x 9.
1
Ответ: , 9.
3
23. Стр. 258, задача 6
24.
Решите уравнения:lg x 2 lg x 1 0
2
3 log 0 , 5 x 5 log0 , 5 x 2 0
2
25. Метод введения новой переменной:
Признак:Все логарифмы
в уравнении могут быть
сведены к одному и тому же
логарифму, содержащему
переменную
1. Определить ОДЗ уравнения
(подлогарифмические
выражения положительны);
2. Произвести замену
переменной;
3. Решить полученное
уравнение;
4. Составить простейшие
логарифмические уравнения,
возвращаясь к
первоначальной переменной;
5. Проверить полученные корни
по ОДЗ;
6. Записать удовлетворяющие
ОДЗ корни в ответ.
26. 5. Метод логарифмирования обеих частей уравнения:
1.Признак:
переменная
содержится и в основании
степени, и в показателе
2.
степени под знаком
логарифма
Xlgx+2 = 1000
3.
4.
Определить ОДЗ
уравнения
(подлогарифмические
выражения
положительны);
Прологарифмировать
обе части уравнения по
основанию равному
основанию логарифма в
показателе степени;
Вынести показатель
степени за знак
логарифма, пользуясь
свойством логарифма;
Решить полученное
уравнение, пользуясь
методом замены
переменной.
27.
Xlgx+2 = 10001)ОДЗ: Х>0
2) Т. к. обе части уравнения положительны, то
прологарифмируем обе части уравнения по основанию 10:
lgxlgx+2 = lg1000
28.
Xlgx+2 = 10001)ОДЗ: Х>0
2) Т. к. обе части уравнения положительны, то
прологарифмируем обе части уравнения по основанию 10:
lgxlgx+2 = lg1000
( lgx+2)·lgx=lg1000
lg2x+ 2lgx- 3=0
lgx=а
а2 + 2а- 3=0
29.
Xlgx+2 = 10001)ОДЗ: Х>0
2) Т. к. обе части уравнения положительны, то
прологарифмируем обе части уравнения по основанию 10:
lgxlgx+2 = lg1000
( lgx+2)·lgx=lg1000
lg2x+ 2lgx- 3=0
lgx=а
а2 + 2а- 3=0
а=- 3 а=1.
lgx=1,
x=10
lgx=- 3,
x=10-3=0,001
Ответ: 0,001; 10.
30.
6. Метод приведения логарифмов кодному и тому же основанию:
Стр.258 задача 8
31.
32.
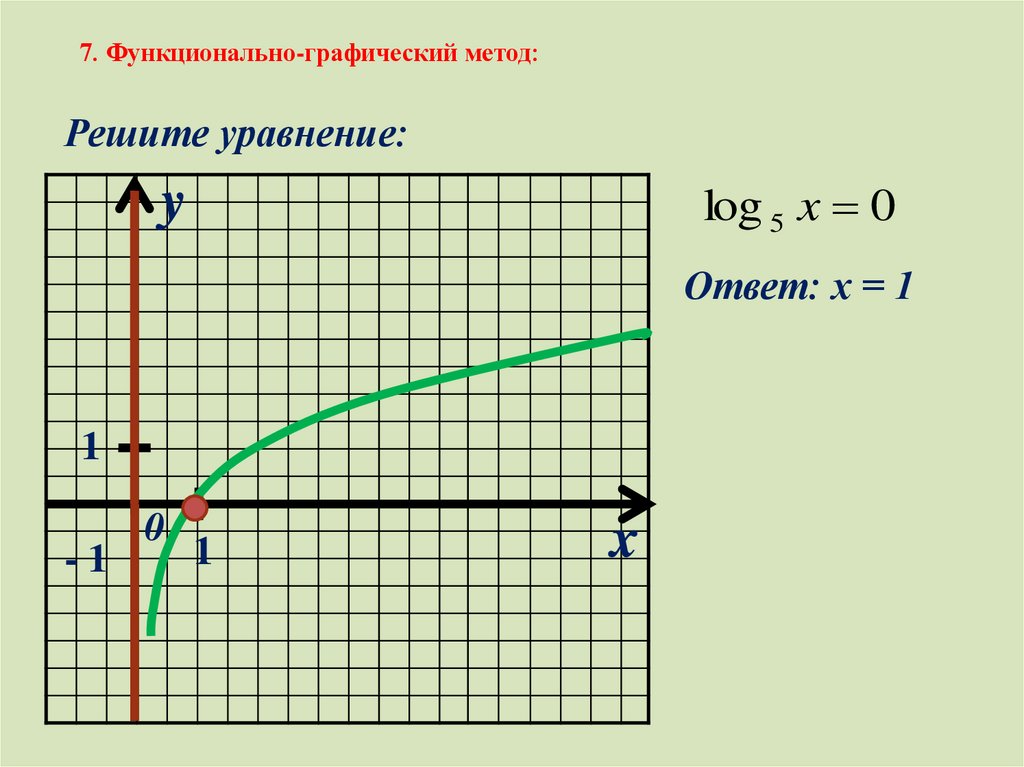
7. Функционально-графический метод:Решите уравнение:
log 5 x 0
y
Ответ: х = 1
1
-1
0
1
x
33.
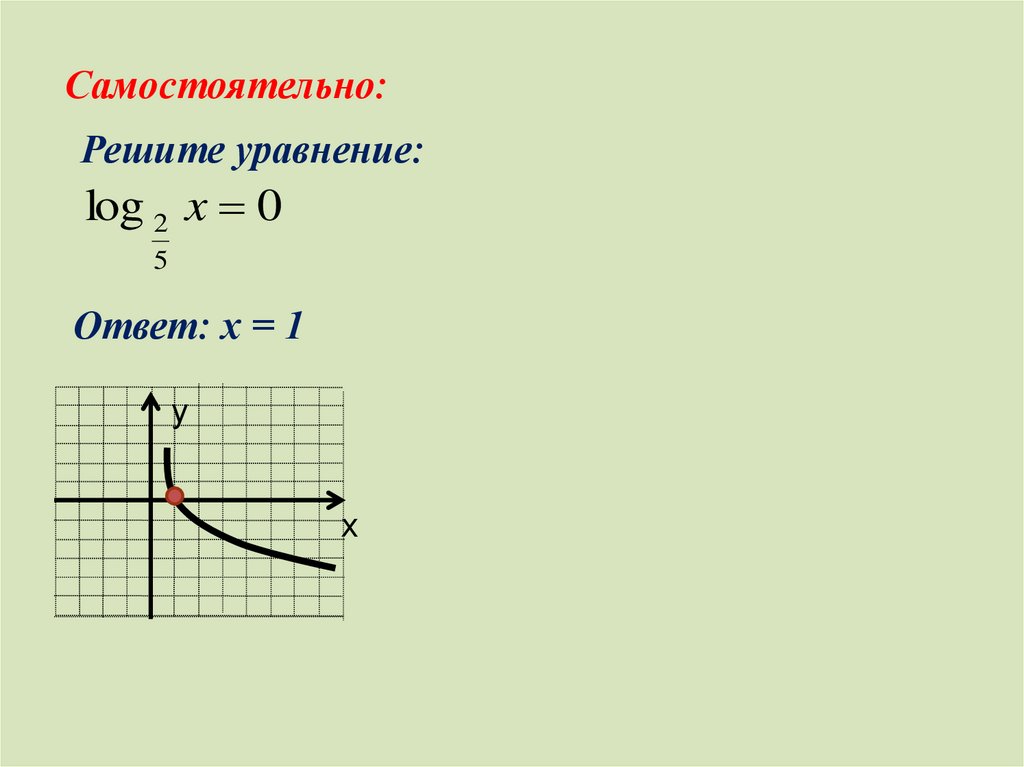
Самостоятельно:Решите уравнение:
log 2 x 0
5
Ответ: х = 1
у
х
34.
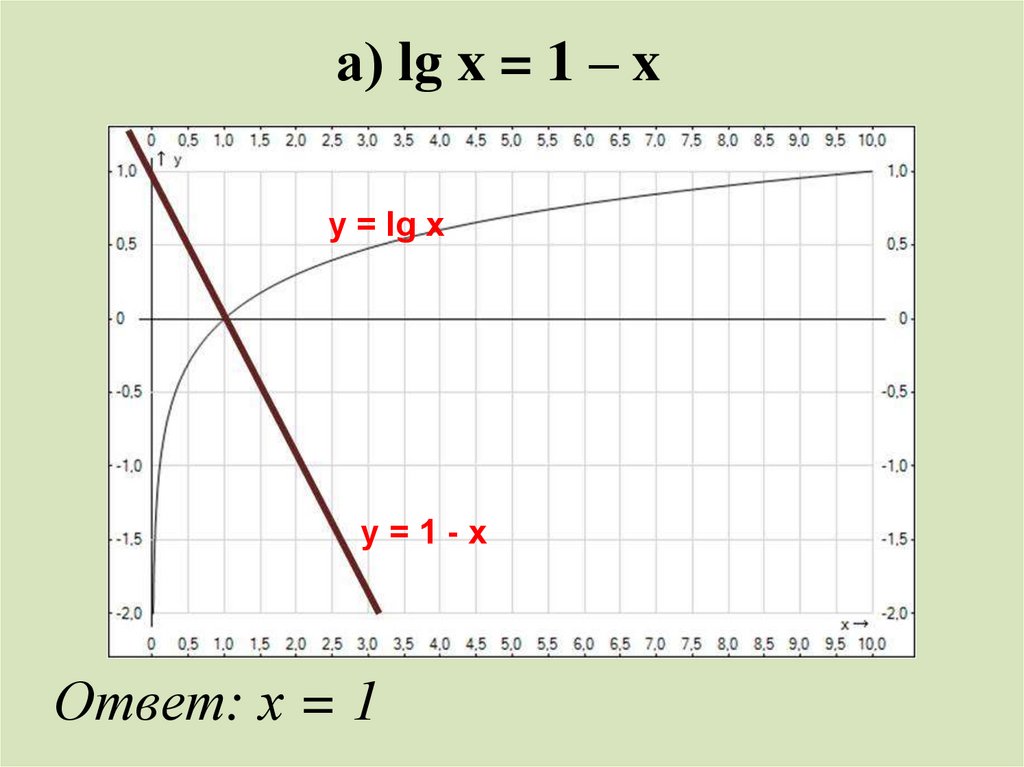
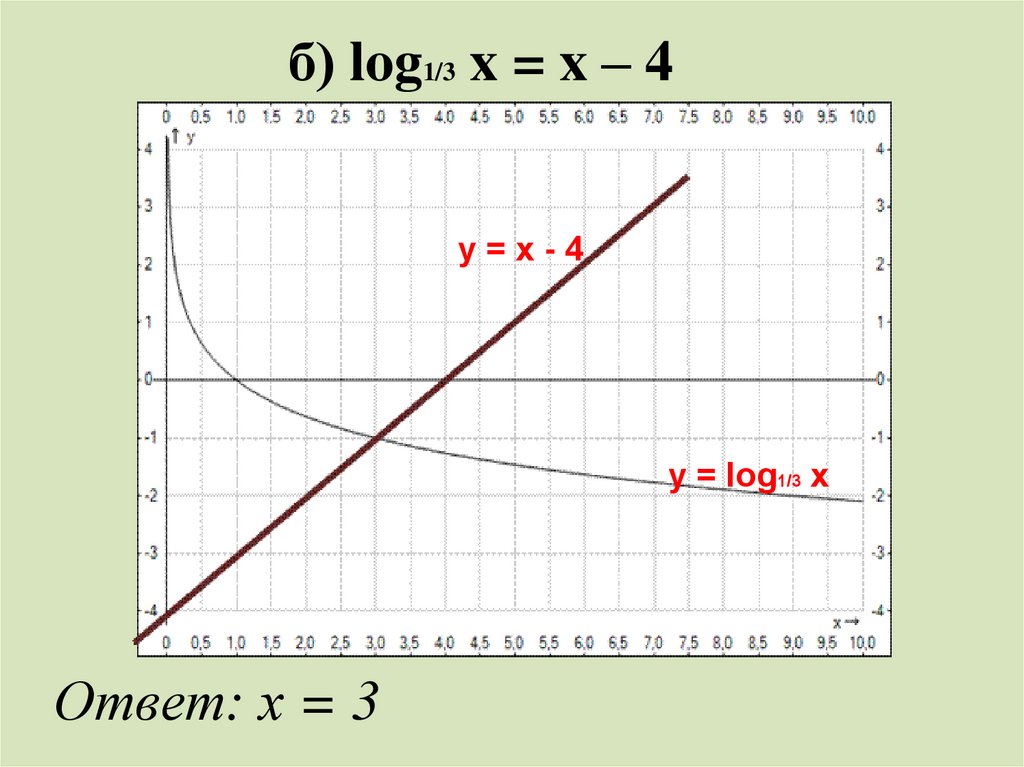
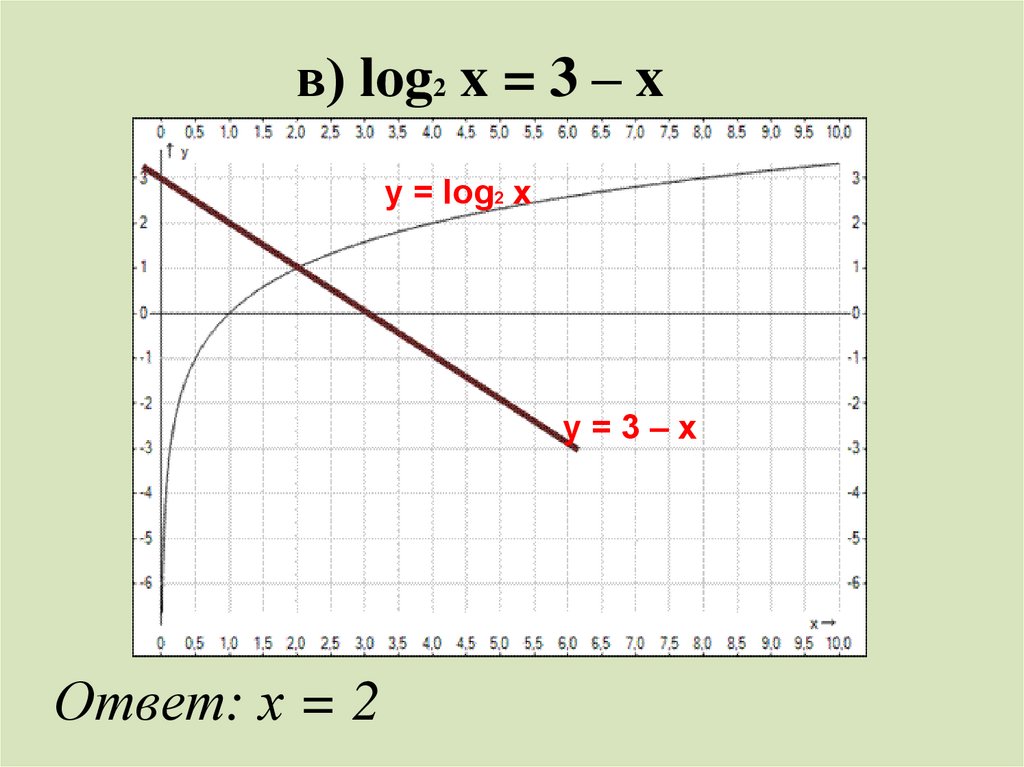
Решите графически уравнения:а) lg x = 1 – x;
б) log1/3 x = x – 4;
в) log2 x = 3 – x.
35.
а) lg x = 1 – xy = lg x
y=1-x
Ответ: х = 1
36.
б) log1/3 x = x – 4y=x-4
y = log1/3 x
Ответ: х = 3
37.
в) log2 x = 3 – xy = log2 x
y=3–x
Ответ: х = 2
38.
Этапы решения уравнения:1. Найти область допустимых
значений (ОДЗ) переменной
2. Решить уравнение, выбрав метод
решения
3. Проверить найденные корни
непосредственной
подстановкой
в исходное уравнение или выяснить,
удовлетворяют ли они условиям ОДЗ



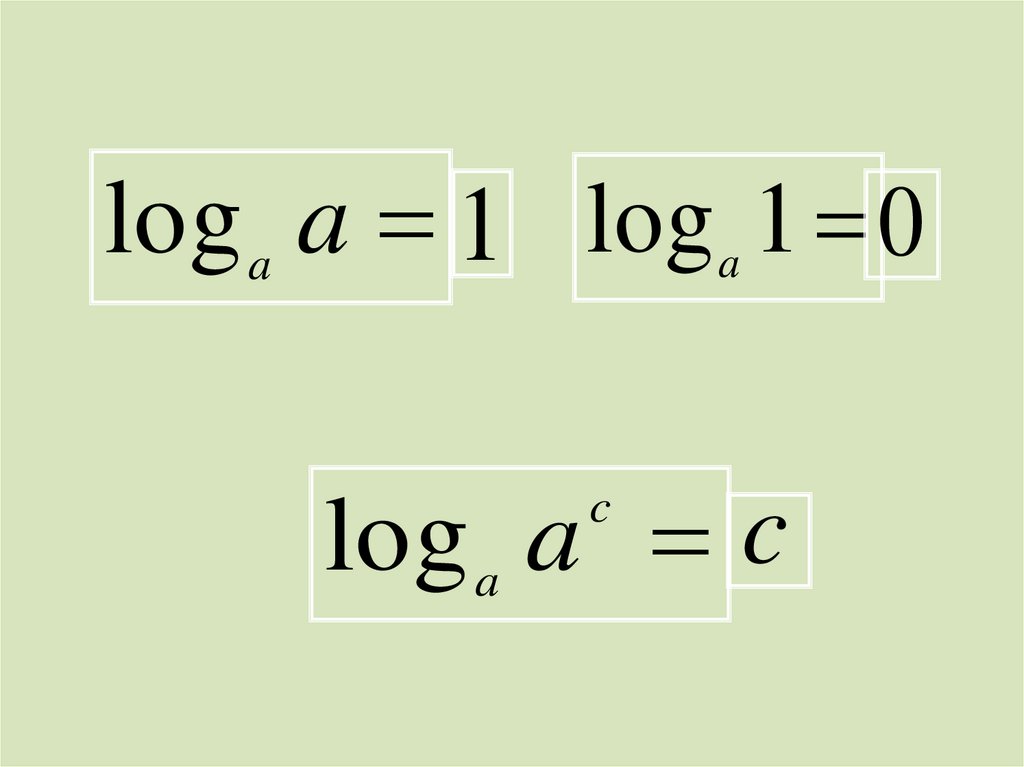



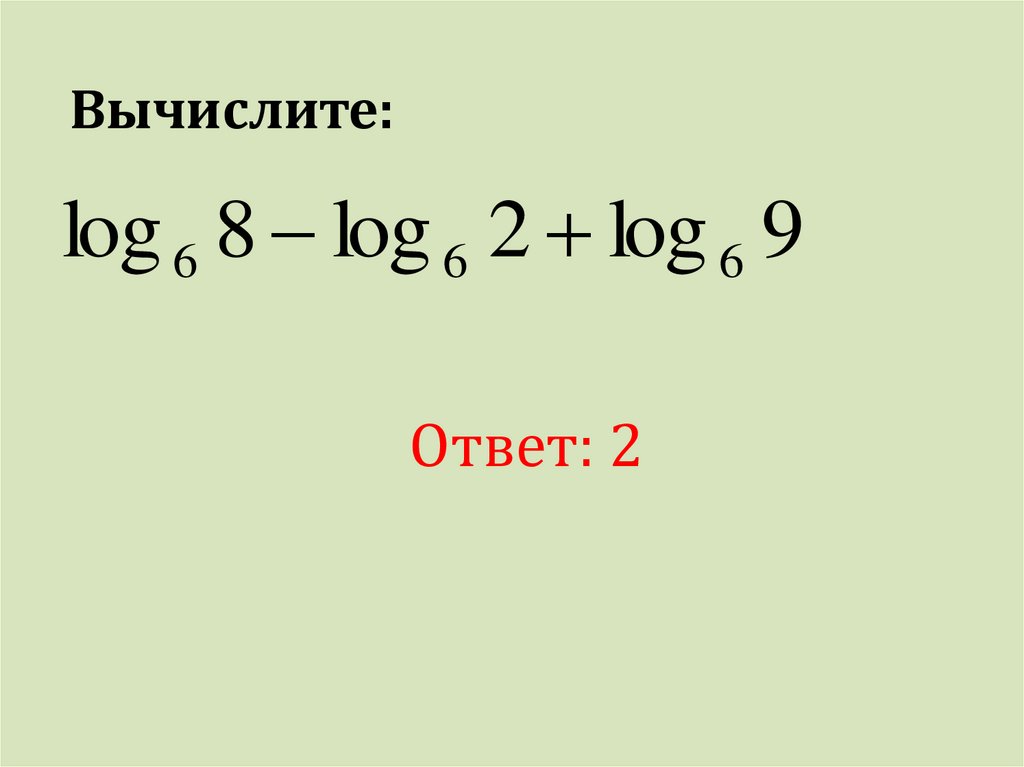



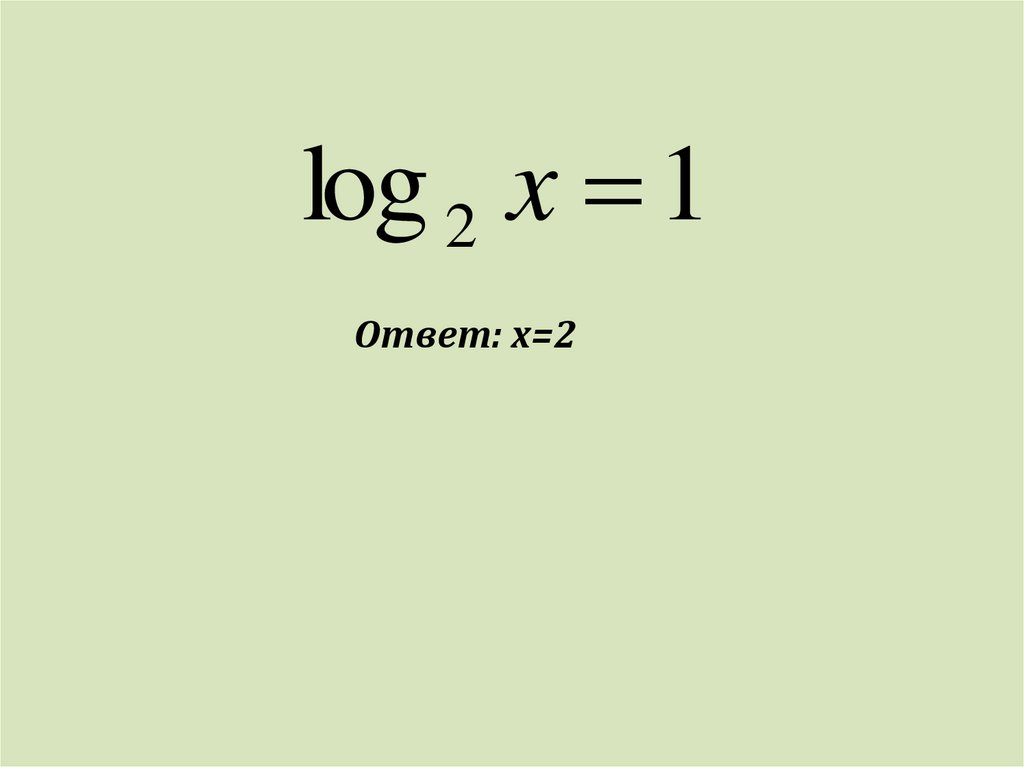



















 mathematics
mathematics








