Similar presentations:
Логарифмические уравнения
1. Логарифмические уравнения.
Муниципальноеобщеобразовательное бюджетное
учреждение «Средняя
общеобразовательная
школа с. Иннокентьевка»»
Логарифмические уравнения.
«Уравнение – это золотой ключ, открывающий все
математические сезамы»
Учитель математики Кокряцкая Т.В..
2. Цели урока:
•образовательная: формирование знаний о разных способахрешения логарифмических уравнений, умений применять их в
каждой конкретной ситуации и выбирать для решения любой способ;
•развивающая: развитие умений наблюдать, сравнивать, применять
знания в новой ситуации, выявлять закономерности, обобщать;
формирование навыков взаимоконтроля и самоконтроля;
•воспитательная: воспитание ответственного отношения к учебному
труду, внимательного восприятия материала на уроке, аккуратности
ведения записей.
3.
Вычислить:log 2 8 3
log 416 2
lg 0,01 2
log 1
log 3 81 1
1
log 3
4
81
1
log 5
2
25
lg 1000 3
4.
Вычислить:1
log 3
5
243
1
log 1
2
9
3
log 6 1
0
log 1 49 2
7
log 3 27 6
log 2 8 6
log
1
3
log 3
27 6
1
3
2
5. Найти логарифмы чисел:
log a 55
1
log a a 1
2
log a a 2
4
log a a 4
log a a
4
log a4 a 1
a
1
log a
a
1
1
log a a
2
1
log a 3 3
2
a
6. Вычислить с помощью тождества:
2log2 4
log2 32
4
loga b
b
log3 3
1
3
a
3
1
2
log1 1
32
2
lg100
10
100
log2 5
log5 3
2
5
3
2
2
1
25
7.
Вычислить с помощью тождества:a
loga b
b
2 log2 5
20
2
log5 3
25
9
log2 3
9
4
27
log3 2
8
25
log5 10
1
100
2
5
5
log2 , 5 10 1
2,5
25
log5 10 2
8.
Найти значение выражения( считая что a>0, a≠1)
2 log3 10
3
5
8
2 log5 10
2 log8 5
2,5
1 24
log3 10
5 3
90
50
a
a
3 loga 2
a
2
loga 2
8
4 log 2 5
a
a
log
4
a
25
16
9. Методы 1. По определению логарифма.
.Ответ: 4.
2х – 4 = 4;
х = 4.
10. 2. Потенцирование (переход от логарифма данного выражения к самому этому выражению).
2. Потенцирование(
переход от логарифма данного выражения к самому этому выражению).
Решение 1. ОДЗ:
Потенцируем исходное уравнение
получим уравнение 2x + 3 = х + 1. Решаем его: х = -2. Это решение не
подходит ОДЗ, значит, данное уравнение корней не имеет.
,
11. 3. Введение новой переменной.
..
3. Введение новой переменной.
;
Решение. ОДЗ: х > 0.
Пусть
. Дискриминант
D > 0. Корни по теореме Виета:
Ответ: 27;
12. 4. Логарифмирование обеих частей уравнения.
.4. Логарифмирование обеих
частей уравнения.
Решить уравнение:
Решение: ОДЗ: х>0, прологарифмируем обе части уравнения по основанию 10:
Применим свойство логарифма степени:
(lgx + 3) lgx =
(lgx + 3) lgx = 4
Пусть lgx = y
у1 = -4 и у2 = 1.
.
Ответ: 0,0001; 10.





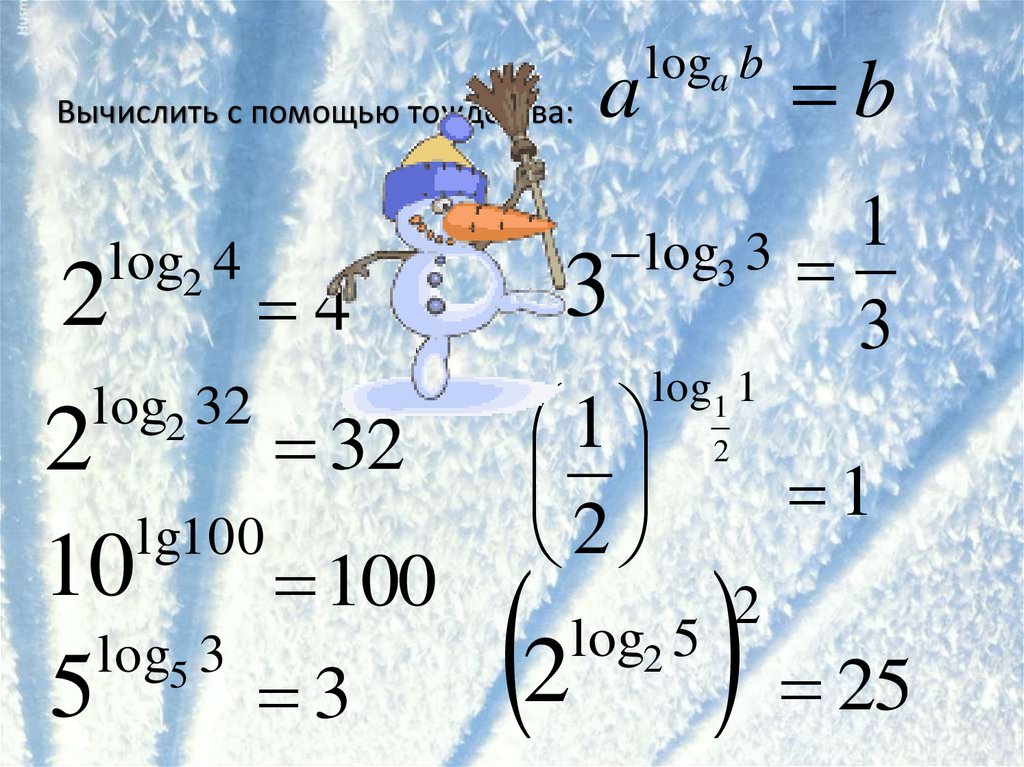
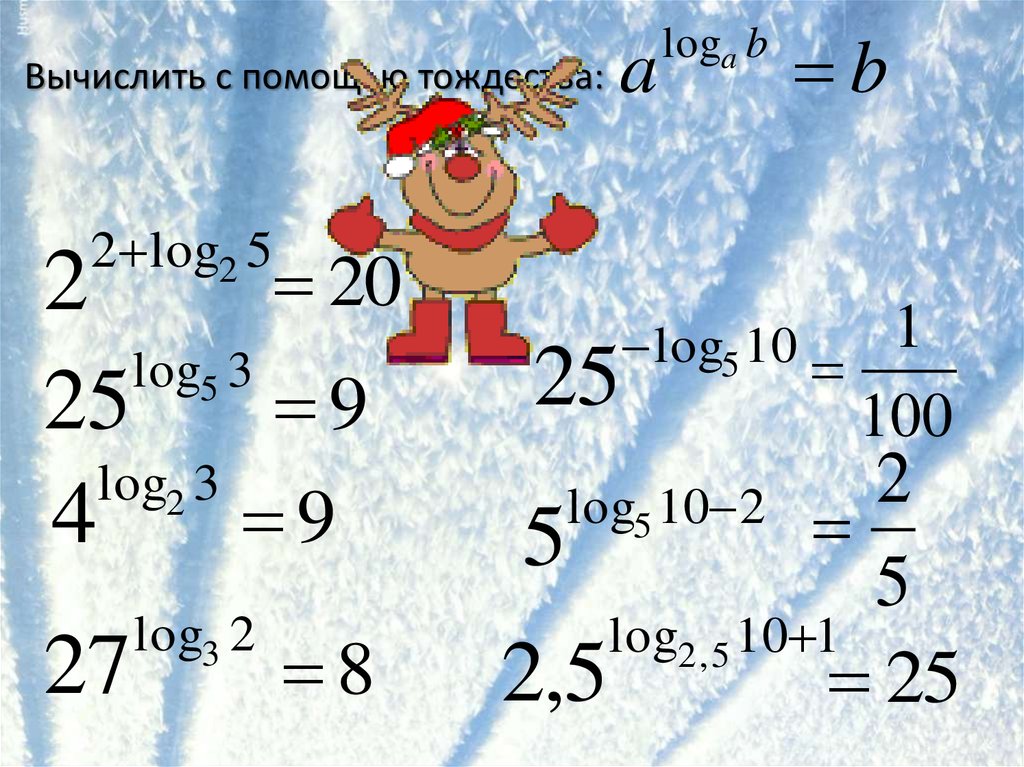








 mathematics
mathematics








