Similar presentations:
Решение логарифмических уравнений к занятию
1. Решение логарифмических уравнений
2. Цель урока:
обобщить материал по свойствамлогарифмов, логарифмической функции;
рассмотреть основные методы решения
логарифмических уравнений;
развивать навыки устной работы.
3. Свойства логарифмов
log a (bc) log a b log a cb
log a
c
log a b log a c
log a b r log a b
r
log a r b
1
log a b
r
log c b
log a b
log c a
4. Основное логарифмическое тождество
aloga b
b
5. Вычислите значения выражения
log 2 8log 5 5
lg 100
log 7 1
log 5 125
lg 0,01
log 4 64
1
log 3
27
log 0,5 32
log 1 9
3
log 2
2
log 3 81
2
log2 5
10
lg15
6. Вычислить значение выражения
log 8 16 log 8 4lg 34 lg 3,4
log 3 log 3 27
3
2 log3 18
log 5 49
log 5 7
7. Вычислить значение выражения
log 3 33 log 3 11lg 25 lg 4
log 2 log 2 16
5
log5 2 1
log 3 64
log 3 4
8. Определение:
Уравнения, содержащие неизвестноепод знаком логарифма или в
основании логарифма называются
логарифмическими.
log a f ( x) b
log f ( x ) b a
9.
Методы решения ЛУ:1.Применение определения
логарифма
Вид уравнения
log a f ( x) b
2.Введение
новой переменной
log 2a f ( x) b log a f ( x) c 0
3. Приведение к одному и
тому же основанию
log a f ( x) log a g ( x)
4. Метод потенцирования
log a f ( x) log a g ( x)
5. Функциональнографический метод
log a f ( x) g ( x)
10.
Решение простейшего логарифмического уравненияlog a f ( x) b,
где a 0, a 1
основано на применении определения логарифма и решении
равносильного уравнения
b
f ( x) a
log 2 3 x 5 4
Пример:
3x 5 2
4
3 x 16 5
3 x 21
Ответ : 7.
11. Метод потенцирования
Под потенцированием понимается переходот равенства, содержащего логарифмы, к
равенству,
не
содержащему
их:
если
log a f ( x) log a g ( x)
то
f ( x) g ( x)
решив полученное равенство, следует
сделать проверку корней.
12.
Пример :log 7 (3 x 4) log 7 (5 x 8)
3x 4 5 x 8
3x 5 x 8 4
2x 4
x 2
Проверка : при x 2
левая и правая части уравнения не имеют смысла
Ответ : нет решений
13.
Уравненияlog a f ( x) b,
f ( x) a
где a 0, a 1
b
равносильные
Уравнения
log a f ( x) log a g ( x)
f ( x) g ( x)
не равносильные, необходима
проверка
14.
log 3 (2 x 1) 2log 3 (2 x 1) log 3 9
2x 1 9
2 x 10
x 5
Проверка : log 3 9 2
Ответ : х 5
15.
log 5 ( x 10) 2 log 5 2log 5 ( x 10) log 5 25 log 5 2
log 5 ( x 10) log 5 50
x 10 50
x 60
Проверка : log 5 50 log 5 50
Ответ : х 60
16.
log 2 ( x 1) log 2 ( x 3) 3log 2 ( x 1) ( x 3) log 2 8
( x 1) ( x 3) 8
x 4x 3 8
2
x 4x 5 0
2
x1 1
x 2 5
Проверка : log 2 2 log 2 4 1 2 3
log 2 ( 4) не существует
Ответ : х 1
17.
log 2 ( x 5) log 2 ( x 2) 3log 2 ( x 5) ( x 2) log 2 8
( x 5) ( x 2) 8
x 3 x 10 8
2
x 3 x 18 0
2
x1 6
x 2 3
Проверка : log 2 1 log 2 8 0 3 3
log 2 ( 8) не существует
Ответ : х 6
18. Если в уравнении содержатся логарифмы с разными основаниями, то прежде всего следует свести все логарифмы к одному основанию,
используя формулы переходаlog a b
log c b
1
1
; log a b
; log a r b log a b
log c a
log b a
r
Пример :
log 2 x 2 log 1 x 9;
2
ОДЗ : x 0
log 2 x 2 log 2 1 x 9;
log 2 x 2 log 2 x 9;
3 log 2 x 9;
log 2 x 3;
x 8 ОДЗ
Ответ : x 8
19.
1) log 2 (2 x 1) 32) log 4 (7 x) 3
3) log 2 (1 2 x) 0
4) lg( x 3) 3 2 lg 5
5) lg( x 2 х) lg 30 1
2















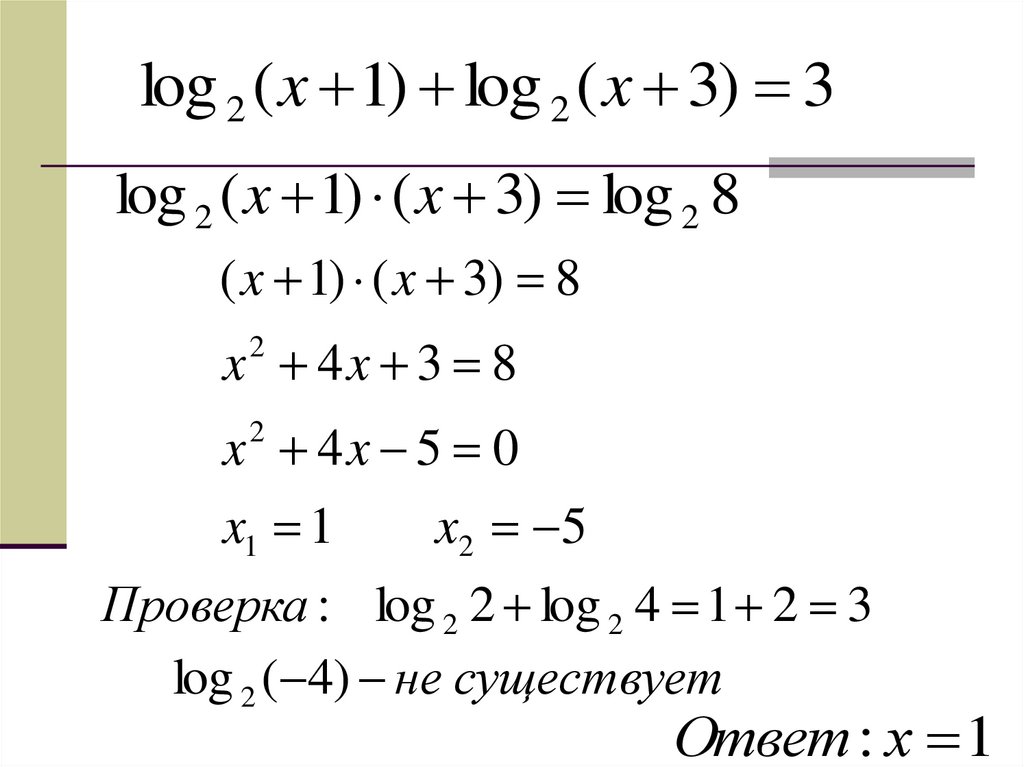



 mathematics
mathematics








