Средняя линия треугольника

1. Презентация к уроку геометрии в 8 классе по теме «Средняя линия треугольника»

Половинкина Т.Н.,
учитель математики «МБОУ Майнский
многопрофильный лицей» Майнского
района Ульяновской области

2. Верно ли?

1. Два треугольника подобны, если их углы
соответственно равны и сходственные стороны
пропорциональны.
2. Два равносторонних треугольника иногда подобны.
3. Если три стороны одного треугольника
соответственно пропорциональны трем сторонам
другого треугольника, то такие треугольники подобны.
4. Если два угла одного треугольника равны 60 и 50 , а два
угла другого треугольника равны 50 и 70 , то такие
треугольники подобны
5. Если две стороны одного треугольника пропорциональны
двум сторонам другого треугольника, то такие
треугольники подобны

3.

Задача 1
А
Д
8
4
10
5
6
К
С
Найти: КВ
В

4.

Задача
В
К
4
А
Е
С
18
15
5
6
12
М
Р
Д
Доказать:
АКР~
СМЕ

5.

«Я могу ошибаться, и ты
можешь ошибаться, но
совместными
усилиями
мы можем постепенно
приближаться к истине».
К.Поппер

6.

• обозначьте треугольник АВС;
• отметить середины стон АВ и ВС
обозначить их М и N;
• соединить полученные точки отрезками.

7.

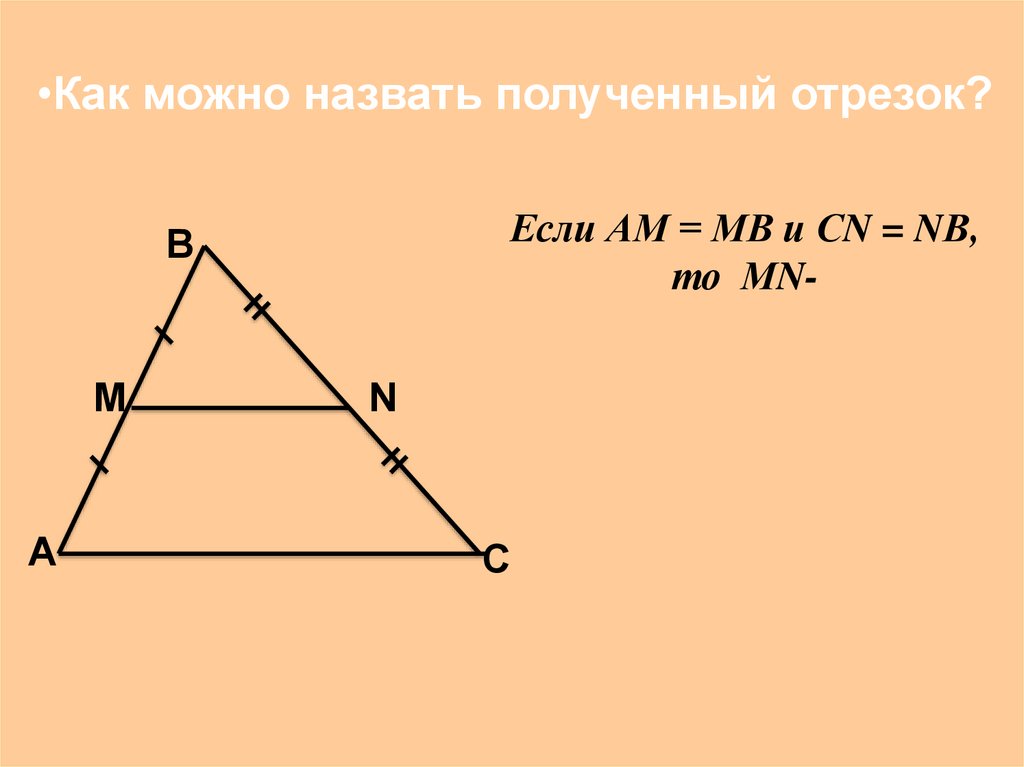
•Как можно назвать полученный отрезок?
Если АМ = МВ и СN = NВ,
то МN-
В
М
А
N
С

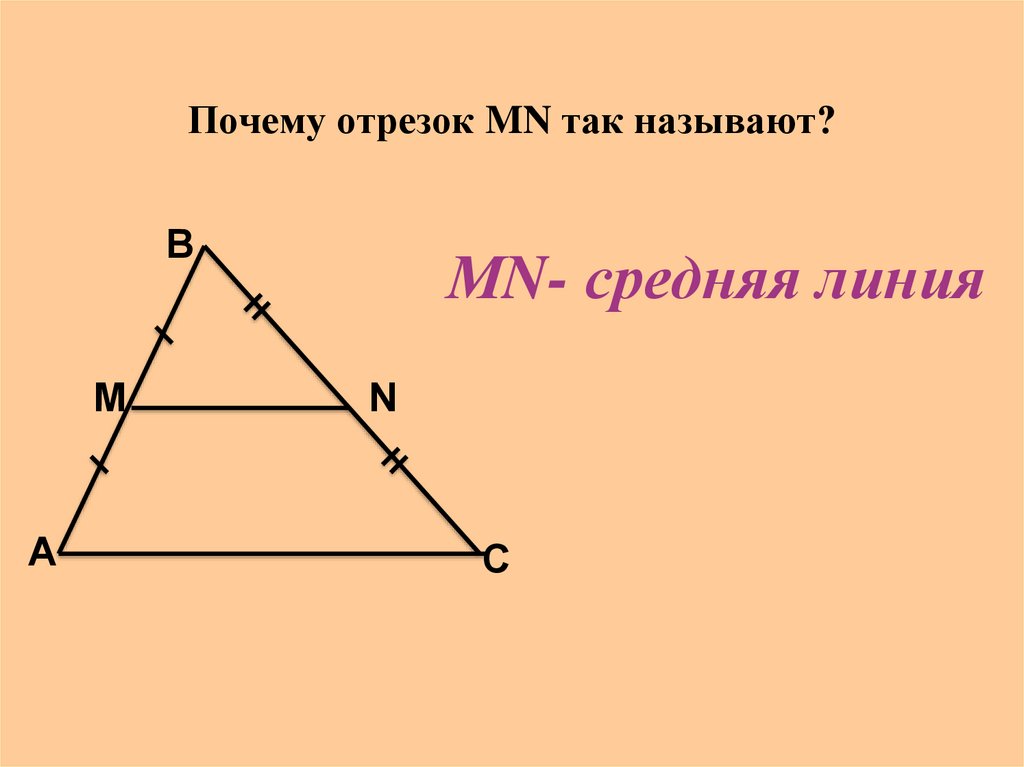
8. Почему отрезок MN так называют?

В
М
А
МN- средняя линия
N
С

9. Средняя линия треугольника

08.02.17
Классная работа.
Средняя линия
треугольника

10. Используя принцип построения, попробуйте сформулировать определение средней линии.

В
М
А
N
С

11. Средней линией треугольника называется …

В
М
А
N
С

12. Средней линией треугольника называется отрезок, соединяющий середины двух сторон треугольника

В
М
А
N
С

13.

В
М
А
Если АМ = МВ и СN = NВ,
то МN- средняя линия
треугольника
N
С

14.

Является ли отрезок КL средней линией
треугольника АВС
С
5
K
5
А
6
L
6
В

15.

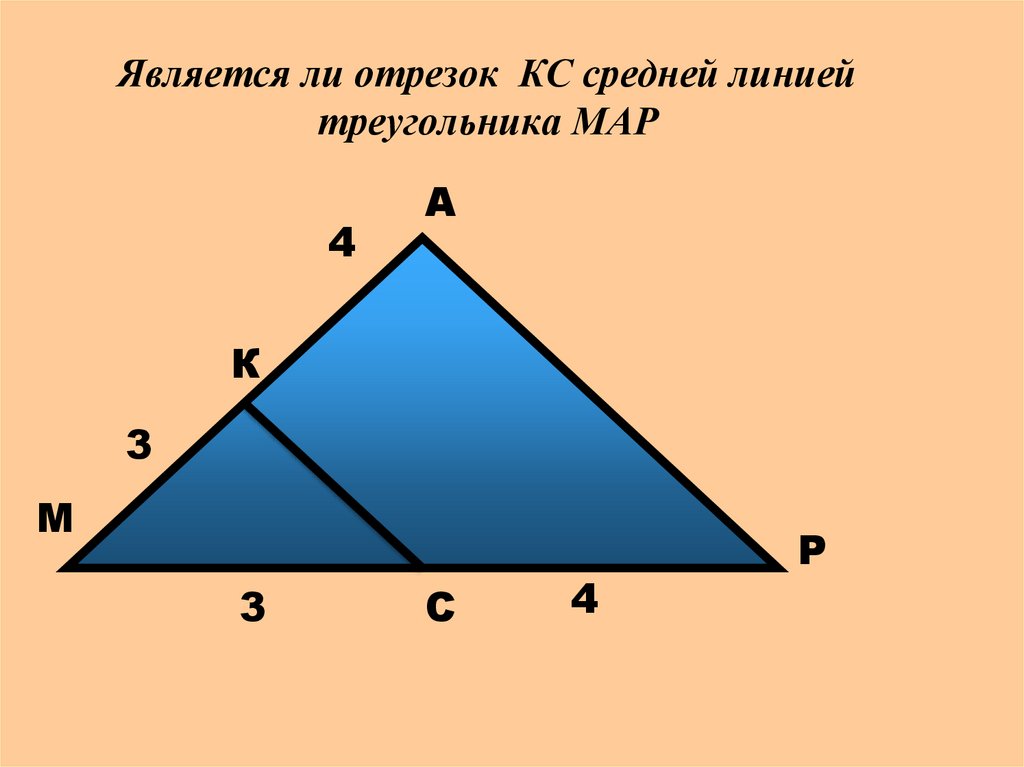
Является ли отрезок КС средней линией
треугольника МАР
4
А
К
3
М
3
С
4
Р

16.

KL – средняя линия треугольника ДFE,
ДF = 10 см, FЕ = 12 см.
Чему равны отрезки ДК, КF, FL, LЕ ?
F
K
Д
L
Е

17. ТВОРЧЕСКОЕ ЗАДАНИЕ

18.

• исследовать, какими свойствами обладает средняя
линия треугольника;
• найдите отношение длин отрезков СВ и МN;
• сформулируйте свойства средней линии
треугольника.

19. Свойства средней линии треугольника.

20. Свойства средней линии треугольника.

• средняя линия треугольника параллельна третьей
стороне и равна её половине ;

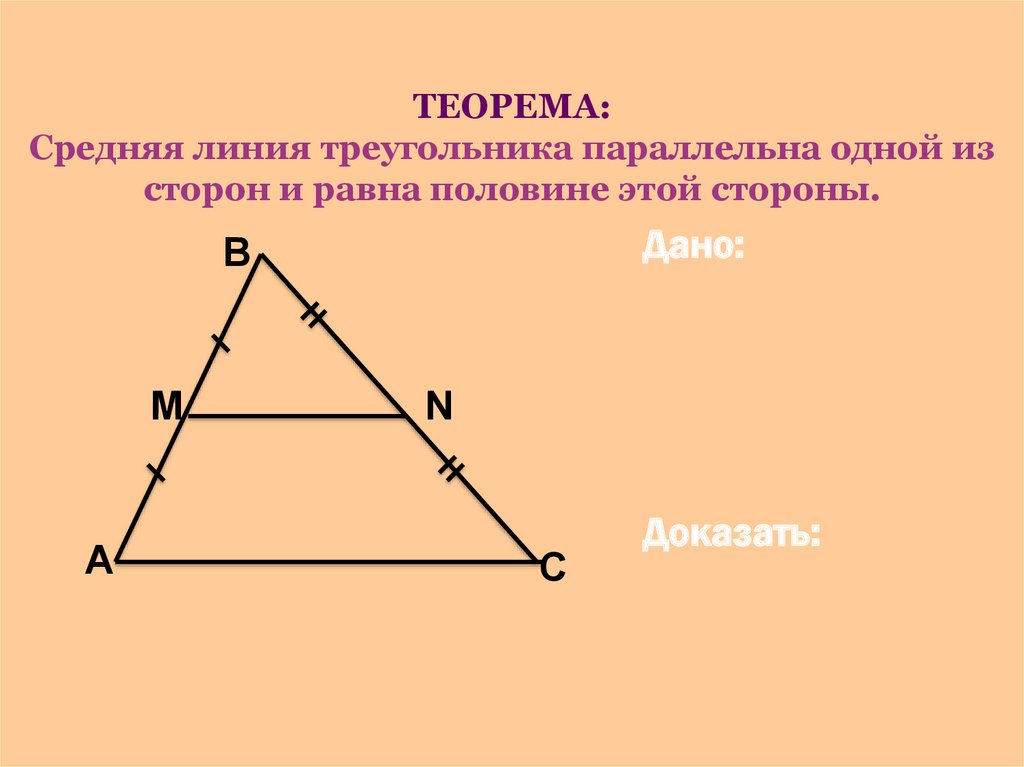
21. ТЕОРЕМА: Средняя линия треугольника параллельна одной из сторон и равна половине этой стороны.

Дано:
В
М
А
N
С
Доказать:

22. Доказательство:

В
М
А
N
С

23. Свойства средней линии треугольника.

средняя линия отсекает треугольник, который подобен
данному, а его площадь равна одной четверти
площади исходного треугольника.

24.

Сколько средних линий можно построить в треугольнике?
С
А
В

25.

С
А
В

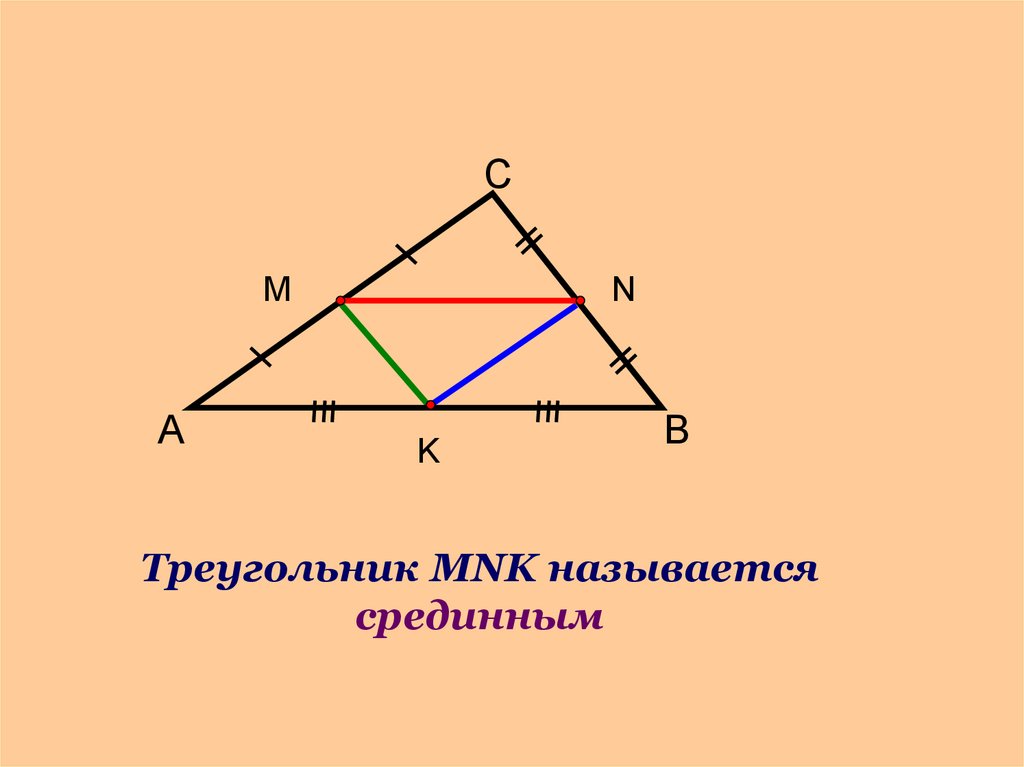
26.

С
М
А
N
K
В
Треугольник MNK называется
срединным

27.

С
А
В
При проведении всех трёх средних линий
образуются 4 равных треугольника, площадь
каждого равна ¼ площади треугольника АВС

28.

№ 564. Дан треугольник со сторонами 8 см, 5 см и 7 см.
Найдите периметр треугольника, вершинами, которого
являются середины сторон данного треугольника.
С
2,55 см
7 см
3,5
N
F
В
А
O
84см

29. Вывод

Периметр срединного треугольника равен ½ площади
самого треугольника

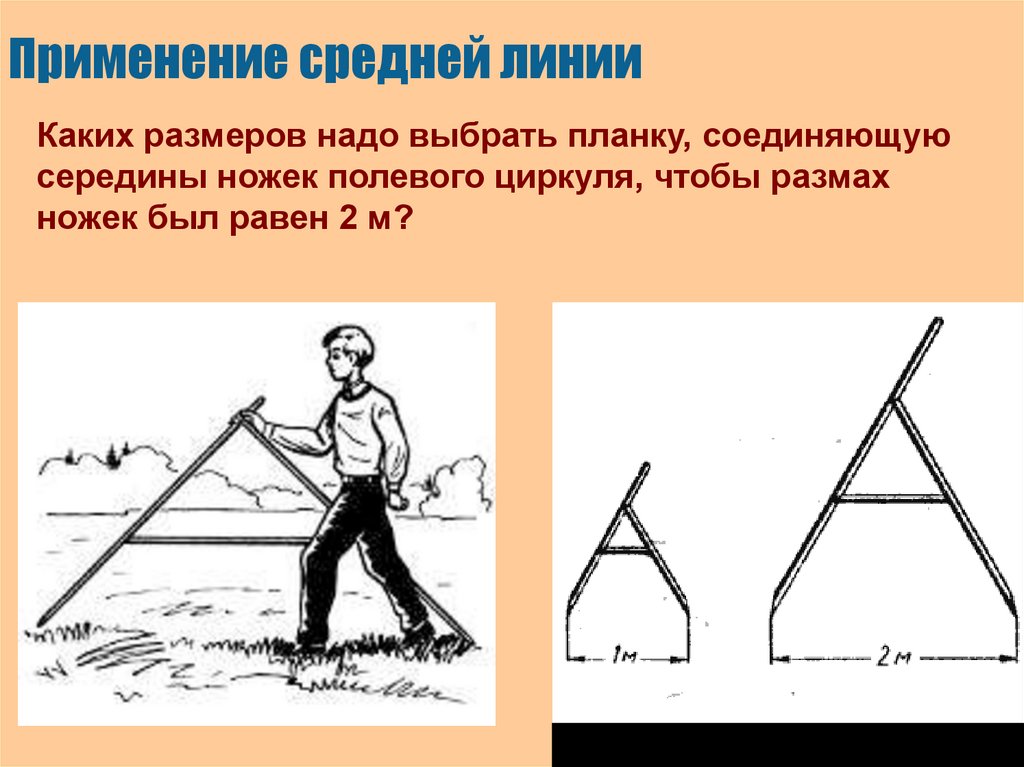
30. Применение средней линии

Для измерения размеров земельных участков
пользуются полевым циркулем.

31. Применение средней линии

Каких размеров надо выбрать планку, соединяющую
середины ножек полевого циркуля, чтобы размах
ножек был равен 2 м?

32. Применение средней линии

Каких размеров надо выбрать планку, соединяющую
середины ножек полевого циркуля, чтобы размах
ножек был равен 2 м?

33.

34.

35. Знания о средней линии можно применять и в строительстве.

• Какой длины надо взять рейки
для перемычек, если ширина
одного пролета 2 м?
• Какой длины надо взять рейки
для перемычек, если ширина
одного пролета 3 м?

36. Итог урока:

Что называется средней линией треугольника
Свойство средней линии треугольника
Домашнее задание :
П 62, вопрос № 8 страница 160 № 565, 567
Дополнительная задача: Доказать что медианы
треугольника пересекаются в одной точке, которая
делит каждую медиану в отношении 2 : 1, считая от
вершины.

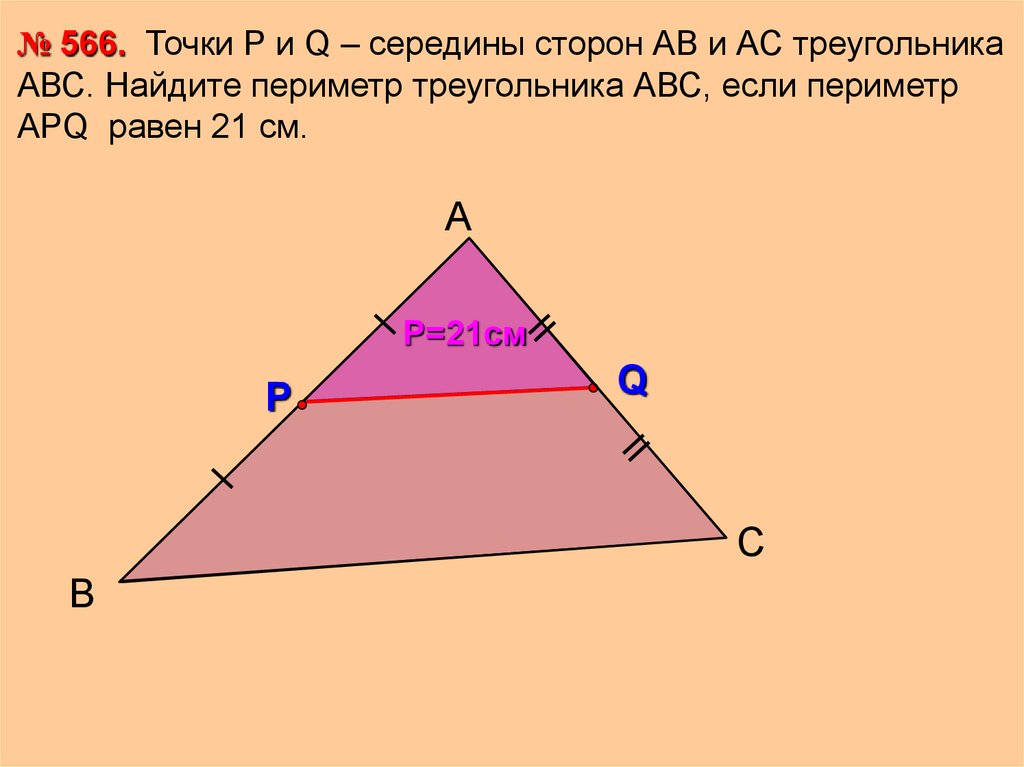
37.

№ 566. Точки Р и Q – середины сторон АВ и АС треугольника
АВС. Найдите периметр треугольника АВС, если периметр
АРQ равен 21 см.
А
Р=21см
Р
Q
С
В

38.

• Рефлексия