Similar presentations:
Средняя линия треугольника и её свойства
1.
Тема урока:«Средняя линия треугольника и её свойства»
2. Определение
Средняя линия треугольника – это отрезок,соединяющий середины двух его сторон.
B
AM=MB, BN=NC
M
N
MN – средняя линия
треугольника
A
C
3. Теорема о средней линии треугольника
Теорема: Средняя линия треугольникапараллельна одной из его сторон и равна
половине этой стороны.
Дано:
АВС
MN – средняя линия
Доказать: MN AC,
B
M
A
N
C
MN= 12 AC
Доказательство:
4.
Теорема: Средняя линия треугольникапараллельна одной из его сторон и равна
половине этой стороны.
Дано: ΔАВС, МN – средняя линия.
В
М
А
Доказать: МN || АС, МN =½ АС
Доказательство:
1. ΔАВС ~ ΔВМN,
т.к. ВМ:ВА = ВN:ВС=1:2
и угол В – общий.
N
2. Угол ВМN равен углу ВАС,
а они соответственные при
прямых МN и АС и секущей АВ.
Значит, МN || АС.
С
3. Т.к. ВМ:ВА =1:2,
то и МN:АС=1:2.
Теорема доказана.
5.
Решаем устноЗадача №1
Является ли отрезок EF средней линией
треугольника АВС?
В
4
Е
4
А
3
F
3
С
6.
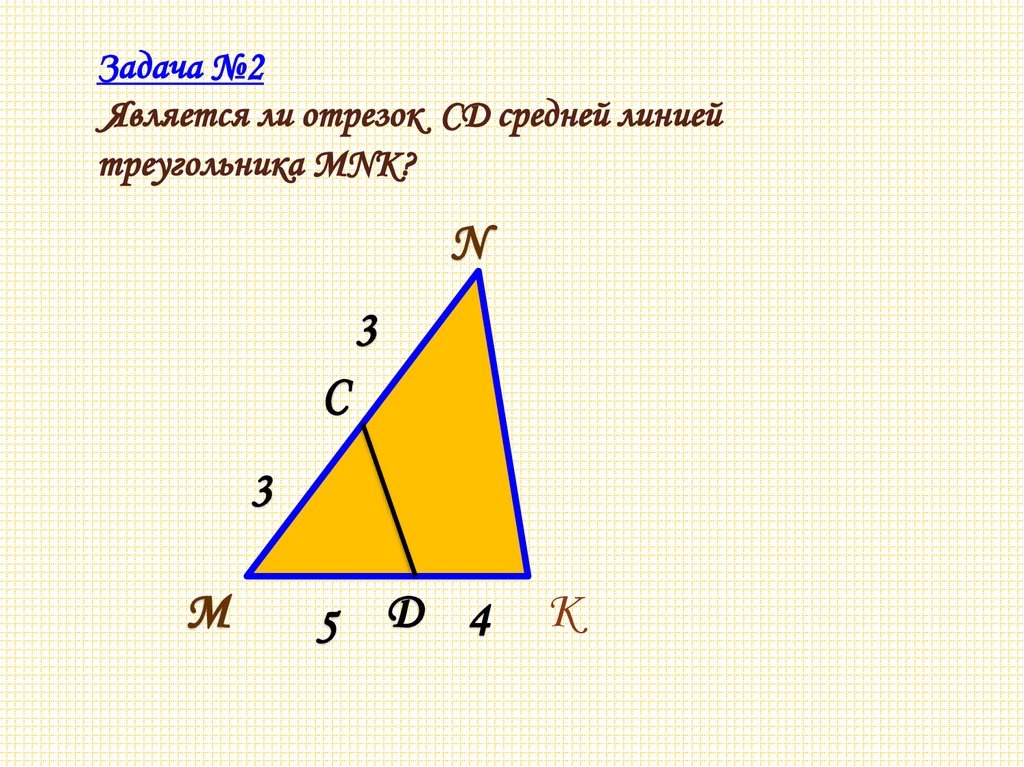
Задача №2Является ли отрезок CD средней линией
треугольника MNK?
N
3
C
3
М
5 D 4
К
7.
Задача №3KL – средняя линия треугольника
DFE, DF =10см, FE= 12 см. Чему равны отрезки DK,
KF, FL, LE?
D
?
10
K
?
F
?
?
12
L
?
E
8.
Задача №4 MK и PK – средние линии треугольникаАВС. Является ли отрезок МР средней линией этого
треугольника?
В
М
А
Р
K
С
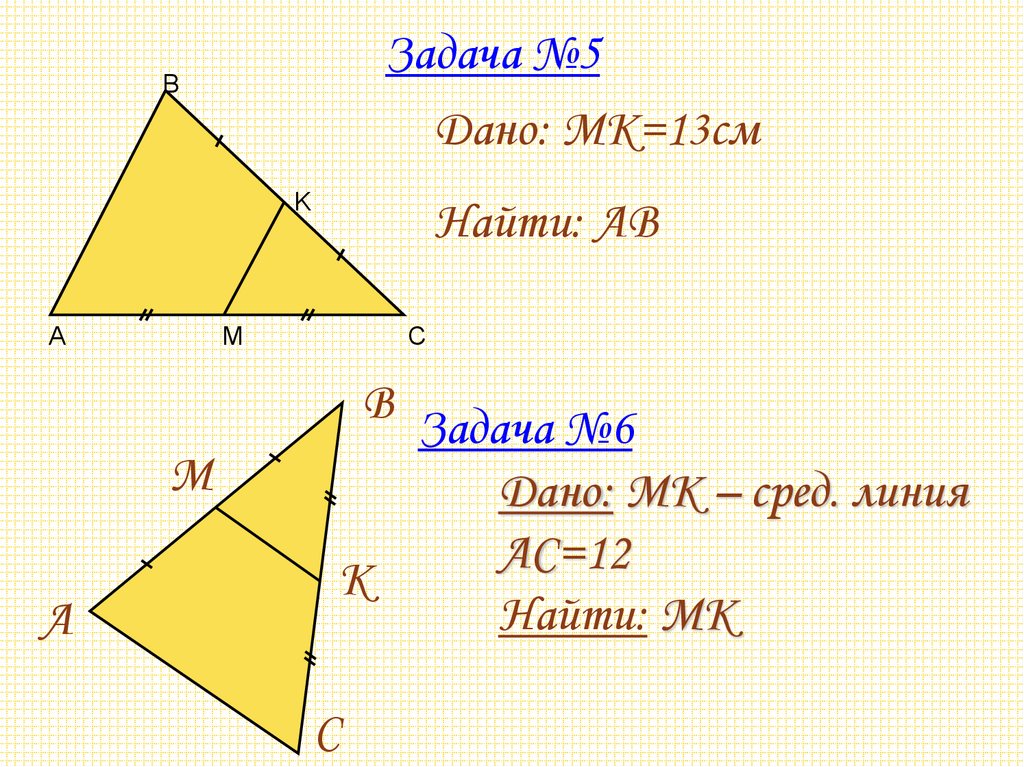
9. Задача №5
Дано: MK=13смB
K
A
Найти: AB
M
C
В Задача №6
М
А
К
С
Дано: MК – сред. линия
АС=12
Найти: MК
10. Задача №7
BM
A
N
K
Дано: AB=10cм, ВС=14см, АС=16см
Найти: периметр MNK
C








 mathematics
mathematics








