Similar presentations:
Средняя линия (8 класс)
1. Средняя линия
(8 класс)2.
Средняя линиятреугольника
3. Средняя линия треугольника.
Определение:Отрезок, соединяющий середины двух сторон треугольника,
называют
СРЕДНЕЙ ЛИНИЕЙ ТРЕУГОЛЬНИКА.
4. Теорема
Средняя линия треугольникапараллельна одной из его сторон и
равна половине этой стороны.
т.е.:
B
K
A
КМ ║АС
M
C
КМ = ½ АС
5.
Дано:MК – сред. линия
АС=12
K
Найти: MК
B
?
M
A
12 см
C
6.
№K
Найти: КС
B
7 см
A
M
2
C
7. Решим задачу :
Дано:MN – сред. линия
Найти: P∆АВС
B
4
3,5
M
3
N
A
C
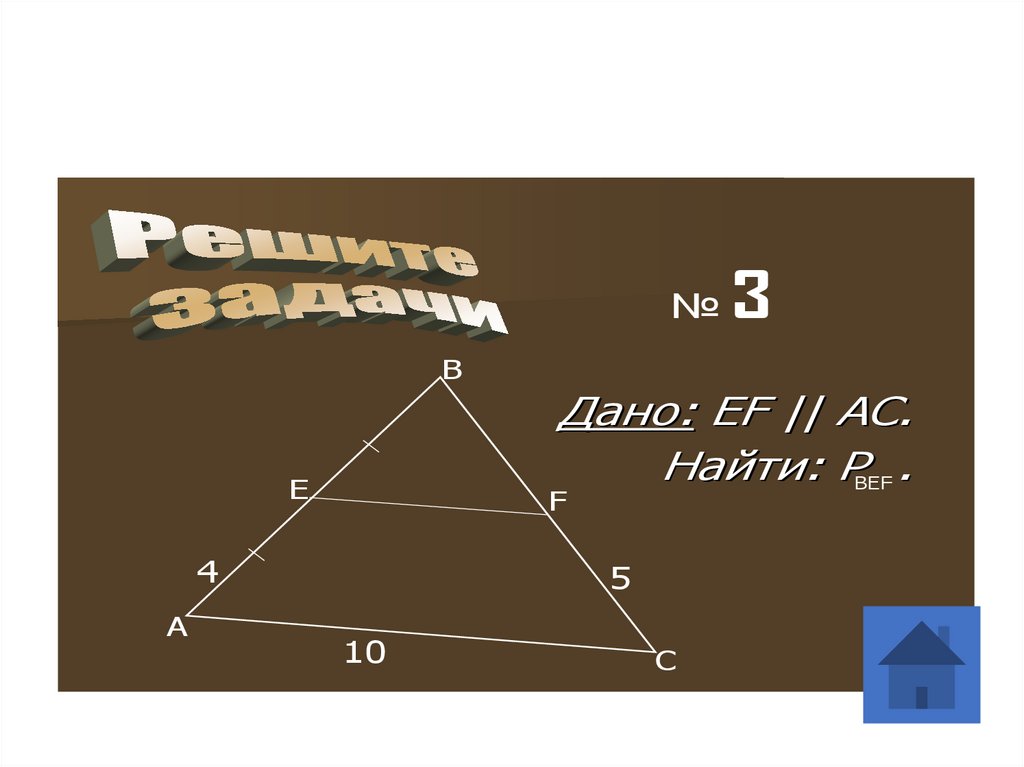
8.
№B
Е
A
Дано: EF || AC.
Найти: РВЕF .
F
4
5
10
3
C
9. Самостоятельная работа
Дано: AC║EF; EB =4; EF =12; FC =5Найти: PABC
В
E
А
F
С
10. Решим задачу
Дано: СD║BE║MK; AD =16; CD =10;MB=4Найти: PAMK
B
C
M
D
А
K
E
11.
Средняя линиятрапеции
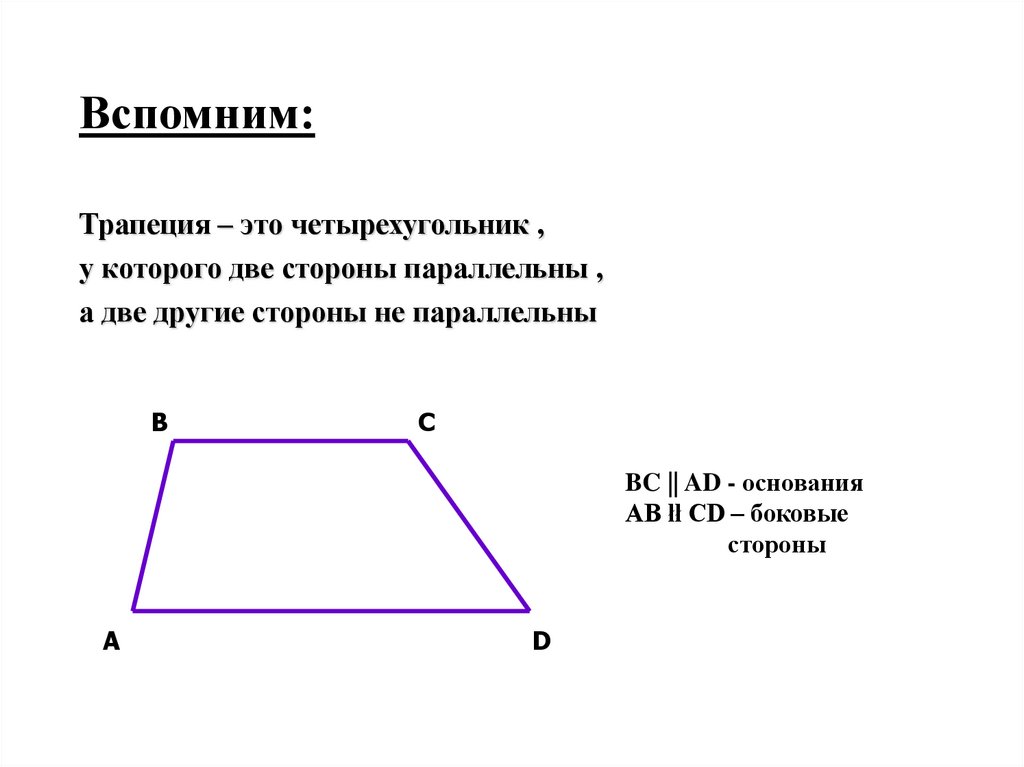
12. Вспомним:
Трапеция – это четырехугольник ,у которого две стороны параллельны ,
а две другие стороны не параллельны
B
C
BC || AD - основания
AB łł CD – боковые
стороны
A
D
13. Средняя линия трапеции.
Определение: Средней линией трапеции называется отрезок,соединяющий середины её боковых сторон.
B
C
MN – средняя линия
M
A
трапеции ABCD
N
D
14. Теорема о средней линии трапеции
Средняя линия трапециипараллельна её основаниям и равна
их полусумме.
B
C
т.е.:
МN║ВС║АD
M
A
N
МN=½(ВС+АD)
D
15. Решить устно:
B6,3 см
M
?
A
18,7 см
C
N
D
16. Решить устно в парах:
Дано: AB = 16 см; CD = 18 см; МN = 15 смНайти: P ABCD = ?
B
M
A
C
N
D
17.
Задача: Средняя линия трапеции равна 5 см. Найтиоснования трапеции, если известно, что нижнее
основание больше верхнего основания в 1,5 раз.
B
х
C
5 см
A
1,5х
D
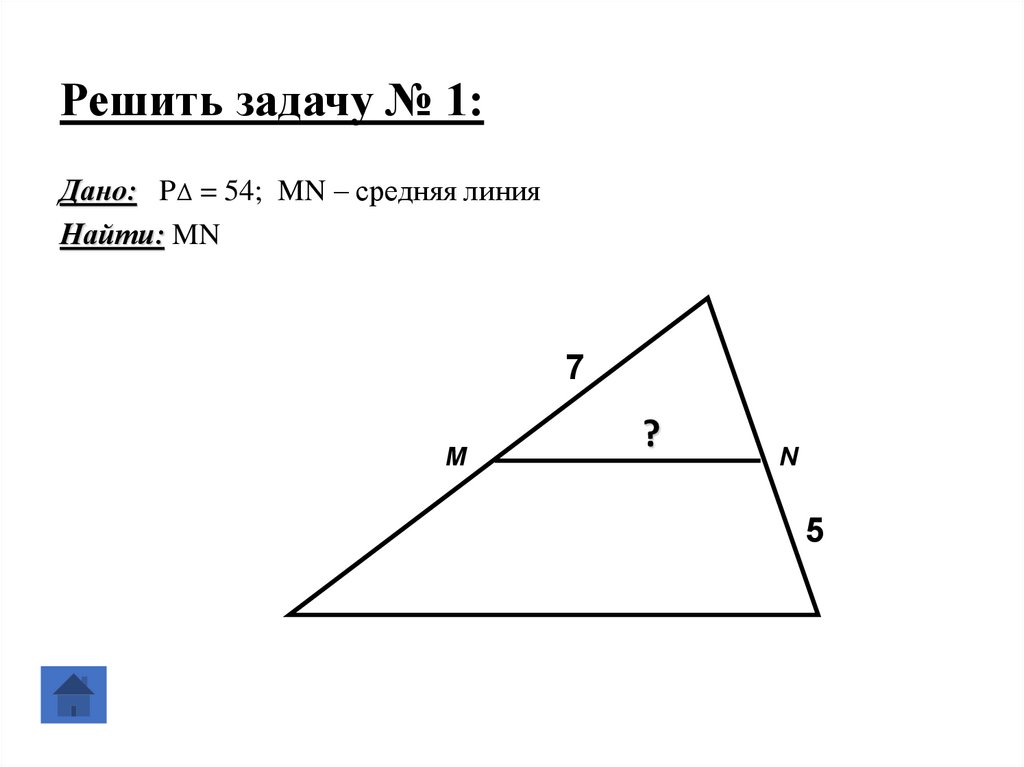
18. Решить задачу № 1:
Дано: PΔ = 54; MN – средняя линияНайти: MN
7
M
?
N
5
19. Решить задачу № 2
Дано: АВСD-трапеция; MN - средняя линияАD=2ВС; ВС=6см
Найти: PQ
B
P
A
C
M
N
K
Q
D
20. Решить задачу № 3
Дано: MN - средняя линия ΔАВС; АС =100ммM1N1 - средняя линия ΔMВN
Найти: M1N1
B
M₁
M
A
?
N₁
N
С
21. Решить задачу № 4:
Дано: АВСD- прямоугольная трапеция; ВС=3СD=4; MN - средняя линия ΔАВD
Найти: MN
В
С
M
?
А
N
D
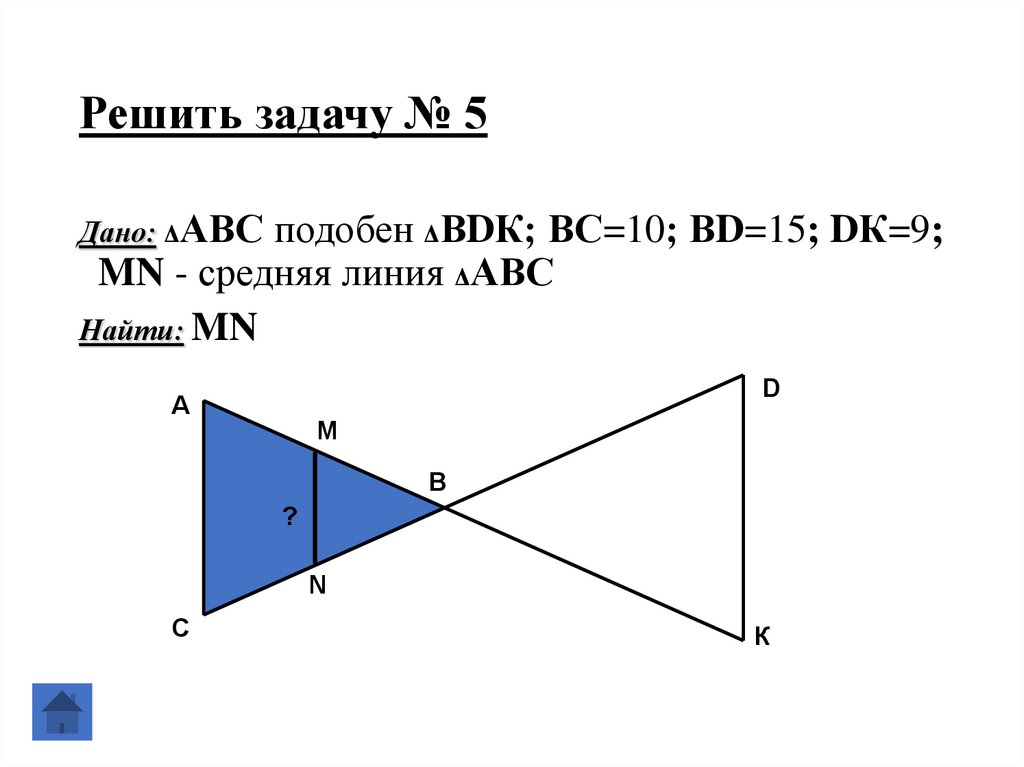
22. Решить задачу № 5
Дано: ΔАВС подобен ΔВDК; ВС=10; ВD=15; DК=9;MN - средняя линия ΔАВС
Найти: MN
D
А
M
В
?
N
С
К
23. Решить задачу № 6
Дано: АВСD-трапеция;ВD =25; СD =10; АВ=12MN-средняя линия ΔАВD
Найти: MN
В
M
A
?
С
N
D
24. Решить задачу № 7
Дано: АВСD-прямоугольник; ВС=17см;О- точка пересечения диагоналей; ОК┴ВС; ОК=4см
Найти: PАВСD
В
K
С
O
А
D
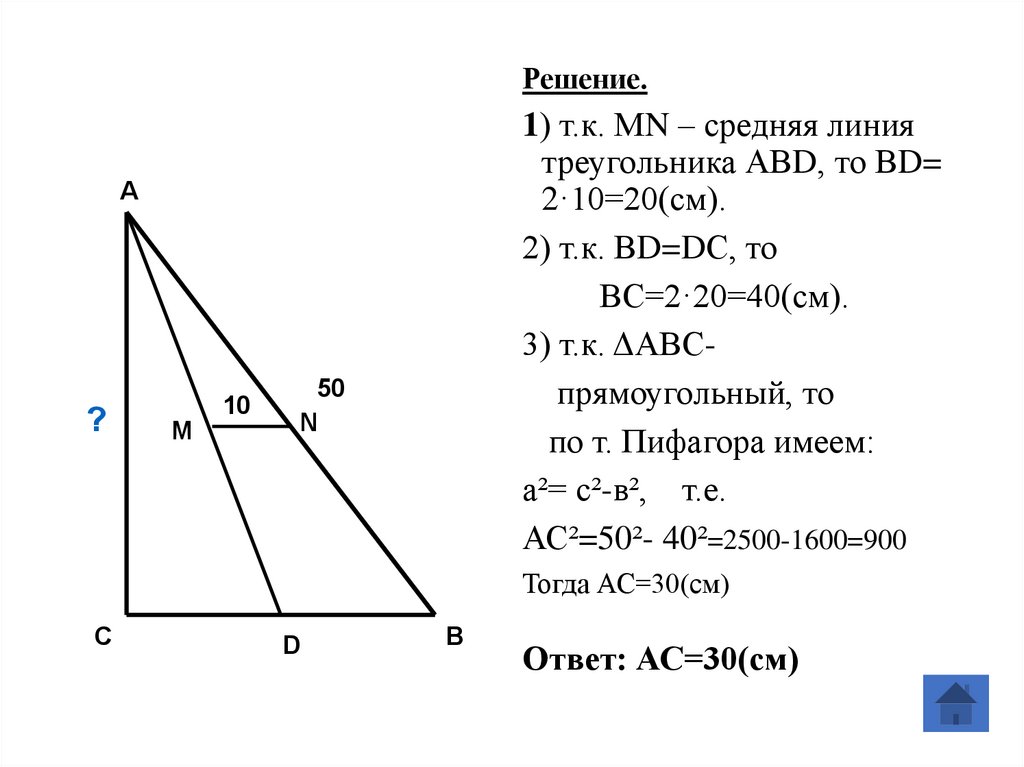
25. Задача № 8.
Дан прямоугольный треугольник АВС.Гипотенуза АВ равна 50 см. Прямая АD
делит сторону СВ пополам. МN –
средняя линия треугольника АВD и
равна 10 см. Найти катет АС.
26.
Решение.1) т.к. МN – средняя линия
треугольника АВD, то ВD=
2·10=20(см).
2) т.к. ВD=DС, то
ВС=2·20=40(см).
3) т.к. ΔАВСпрямоугольный, то
по т. Пифагора имеем:
а²= с²-в², т.е.
АС²=50²- 40²=2500-1600=900
A
?
10
M
50
N
Тогда АС=30(см)
С
D
В
Ответ: АС=30(см)
27. Задача № 9.
Дано:СЕ║ВМ║АК; СЕ+ВМ+АК =21смАВ=4 см; ВС =2см; СD =2см
Найти: АК;СЕ;ВМ
D
C
B
А
Е
M
K
28. Самостоятельная работа
Дано: АВСD – трапеция; MN=8S АВСD = 56; MN- средняя линия
Найти: высоту
В
M
A
С
N
К
D























 mathematics
mathematics








