Similar presentations:
Признаки параллельности прямых
1.
МБОУ СОШ №2г.Югорск
Учитель: Демьянович Е.В.
2.
Задачи урока:•Повторить название углов при
пересечении двух прямых секущей
•Сформулировать признаки
параллельности прямых
•Научиться применять признаки
параллельности прямых при решении задач
3.
Назовите пары углов:а) соответственные
б) внутренние накрест лежащие
в) внутренние односторонние
г) внешние накрест лежащие
д) внешние односторонние
а
b
2
1
3
4
6
5
8
7
c
4.
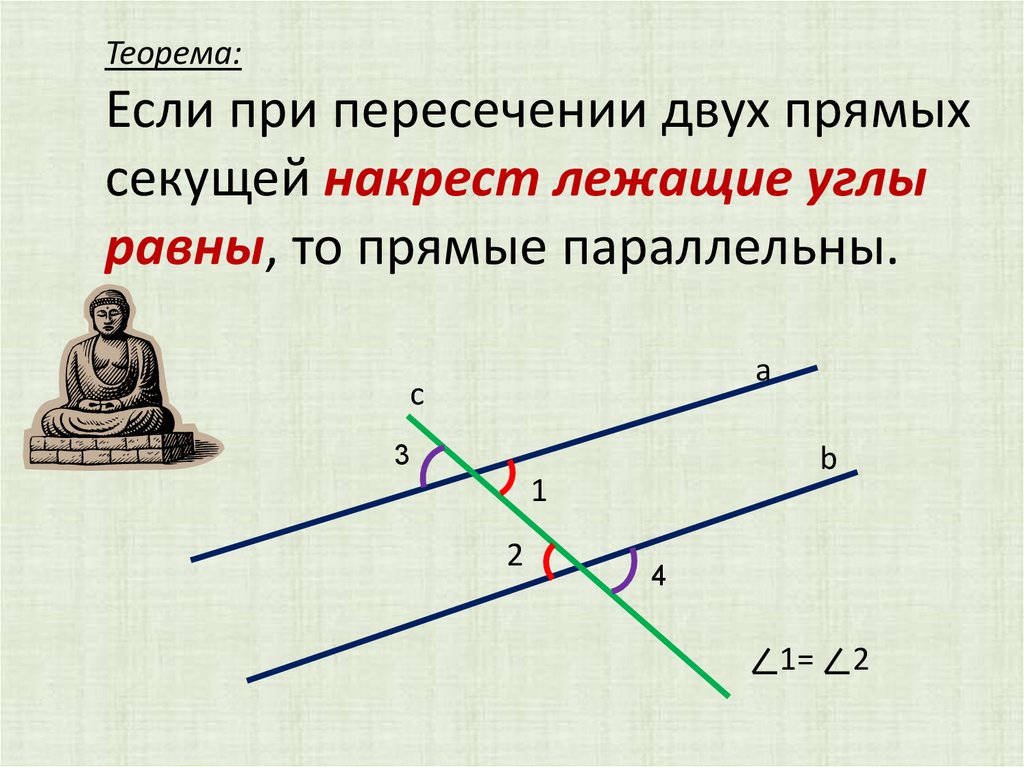
5. Теорема: Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
ас
b
3
1
2
4
1=
2
6.
110⁰1
110⁰
3
45⁰
2
125⁰
123⁰
54⁰
35⁰
4
35⁰
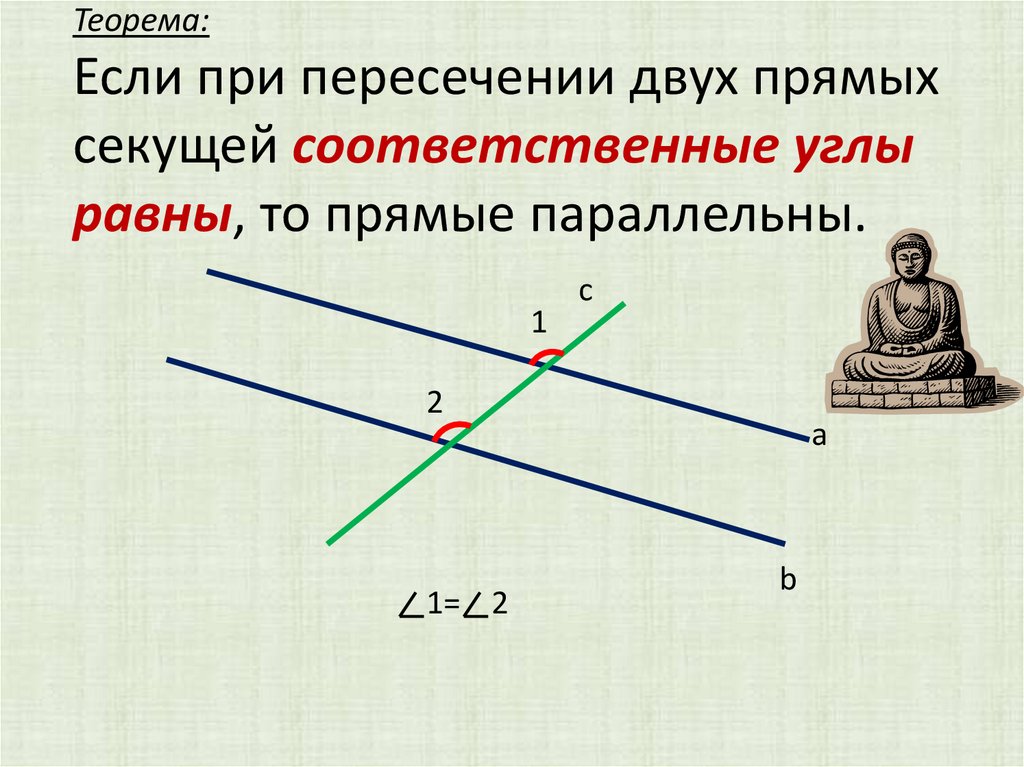
7. Теорема: Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
1с
2
1= 2
а
b
8.
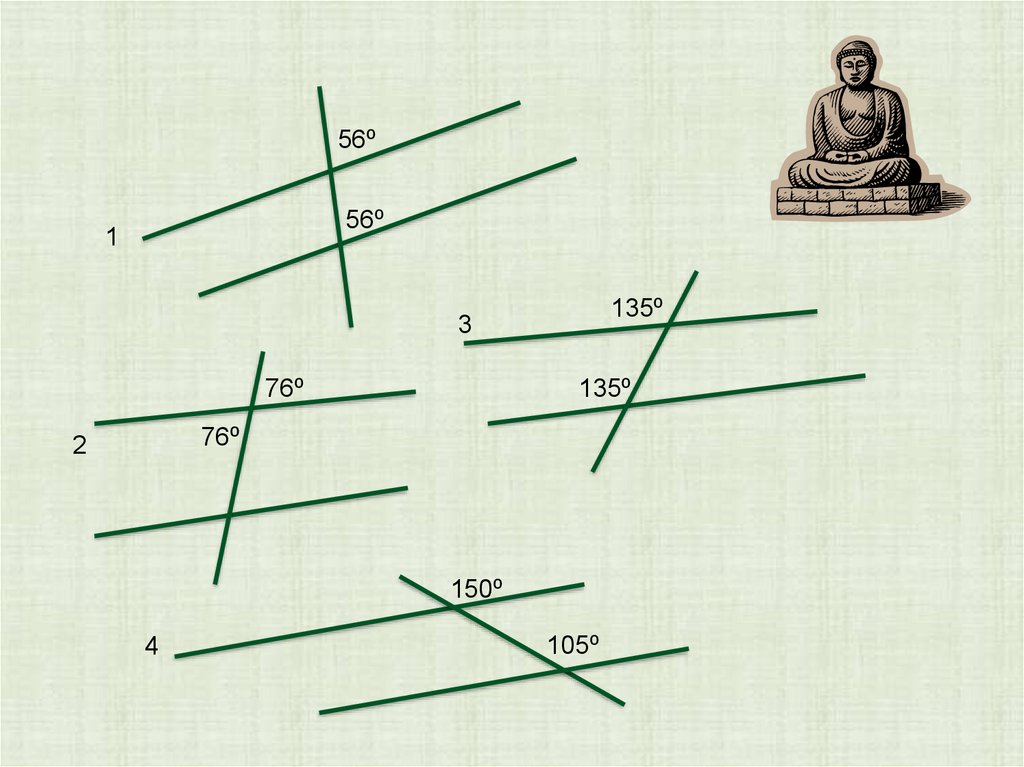
56⁰56⁰
1
135⁰
3
76⁰
135⁰
76⁰
2
150⁰
4
105⁰
9. Теорема: Если при пересечении двух прямых секущей сумма односторонних углов равна 180 , то прямые параллельны.
са
3
1
2
4
1+ 2=180⁰
b
10.
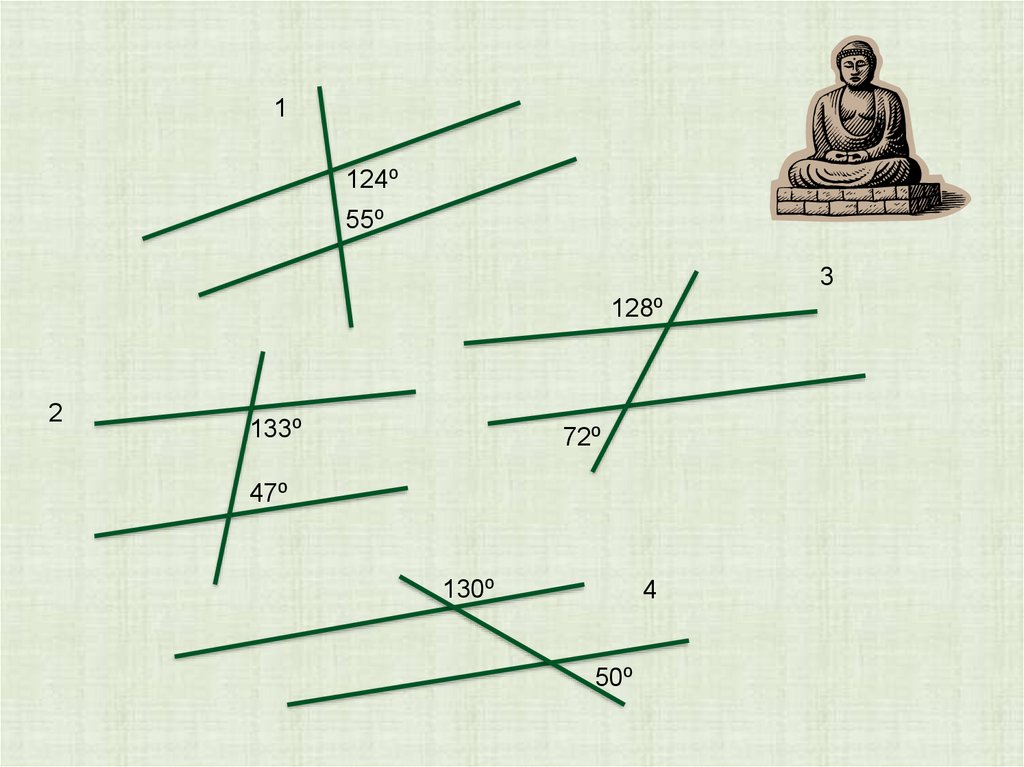
1124⁰
55⁰
3
128⁰
2
133⁰
72⁰
47⁰
130⁰
4
50⁰
11. Вывод: Прямые параллельны, если выполняется одно из следующих условий:
•Накрест лежащие углы равны.•Соответственные углы равны.
•Сумма односторонних углов
равна 180 градусам.
12.
Задачаа
с
2
1
4
b
3
5
8
7
6
Дано: а) 1=37⁰, 7=143⁰; б) 1= 6;
в) 1=45⁰, 7 в три раза больше 3.
Доказать: аІІ b.
Доказательство:








 mathematics
mathematics








