Прямоугольный параллелепипед

1. Прямоугольный параллелепипед

1

2. Цели урока

• Ввести понятие прямоугольного
параллелепипеда;
• Рассмотреть свойства его граней,
двугранных углов и диагоналей;
• Сформировать навык решения
задач о диагонали прямоугольного
параллелепипеда.
2

3. Параллелепипед -

• Призма, основания которой являются
параллелограммы. (параллелограмм –
четырехугольник, у которого
противоположные стороны
параллельны и равны).
• Он имеет 6 граней, каждая из которых
является параллелограммом.
3

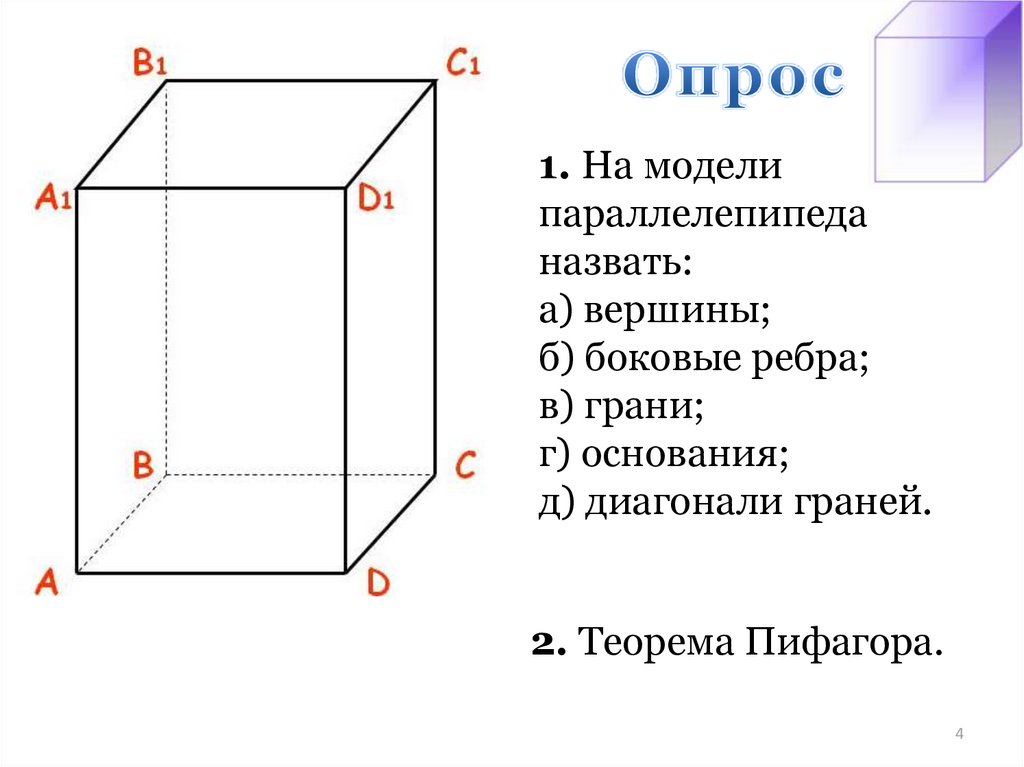
4. Опрос

1. На модели
параллелепипеда
назвать:
а) вершины;
б) боковые ребра;
в) грани;
г) основания;
д) диагонали граней.
2. Теорема Пифагора.
4

5.

–
– все
грани которого
произвольные
параллелограммы
у которого
боковые грани
являются
прямоугольниками
все
грани которого
прямоугольники.
5

6. Примеры параллелепипеда

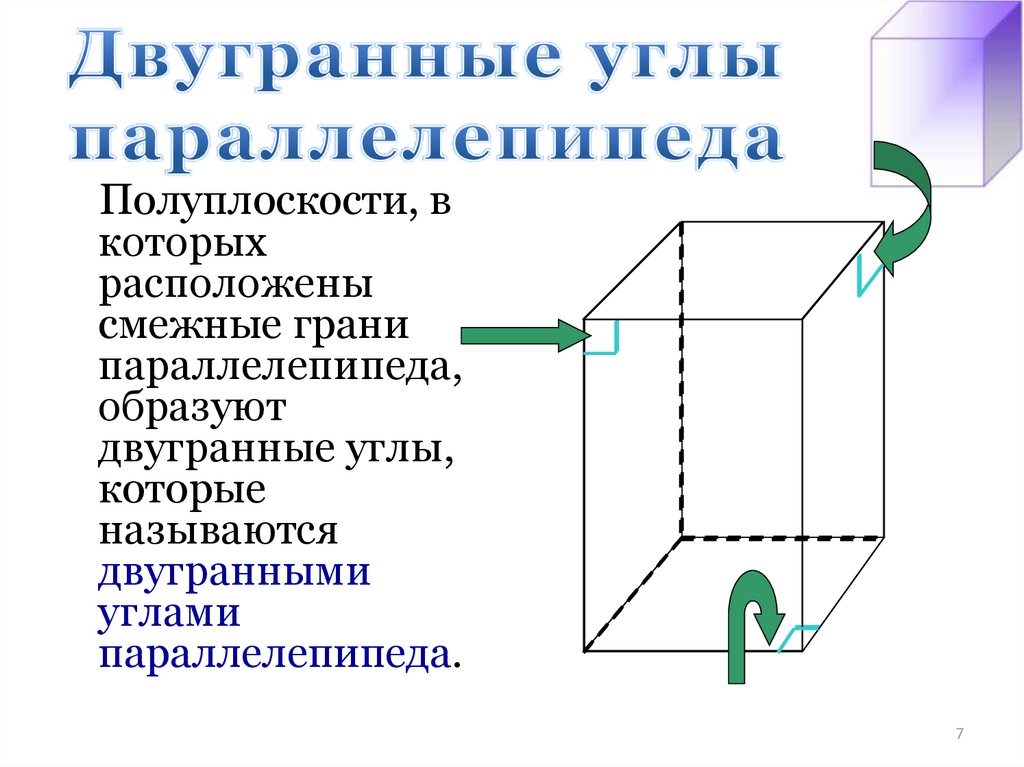
6

7. Двугранные углы параллелепипеда

Полуплоскости, в
которых
расположены
смежные грани
параллелепипеда,
образуют
двугранные углы,
которые
называются
двугранными
углами
параллелепипеда.
7

8. Свойства параллелепипеда

В прямоугольном параллелепипеде
все шесть граней – прямоугольники.
Все двугранные углы прямоугольного
параллелепипеда – прямые.
8

9. Что такое измерения?

Длины трёх рёбер,
имеющих общую
вершину, назовём
измерениями
прямоугольного
параллелепипеда.
У параллелепипеда
ABCDA1B1C1D1 в
качестве измерений
можно взять рёбра
AB, AD и AA1.
B1
A1
C1
D1
B
A
C
D
9

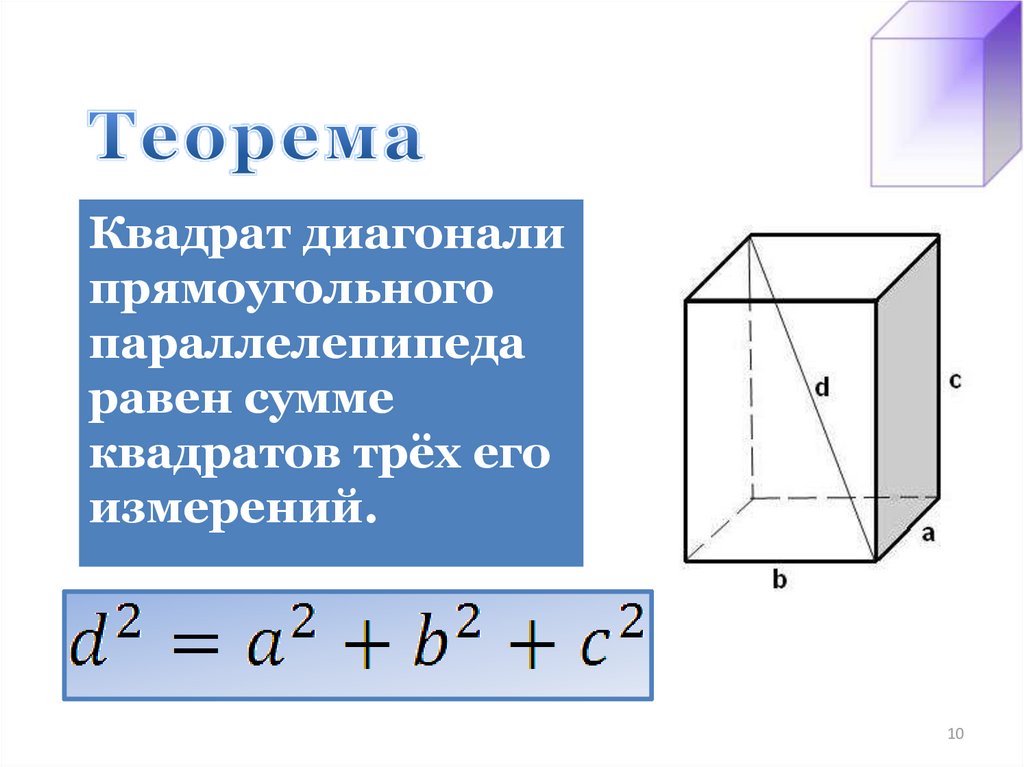
10. Теорема

Квадрат диагонали
прямоугольного
параллелепипеда
равен сумме
квадратов трёх его
измерений.
10

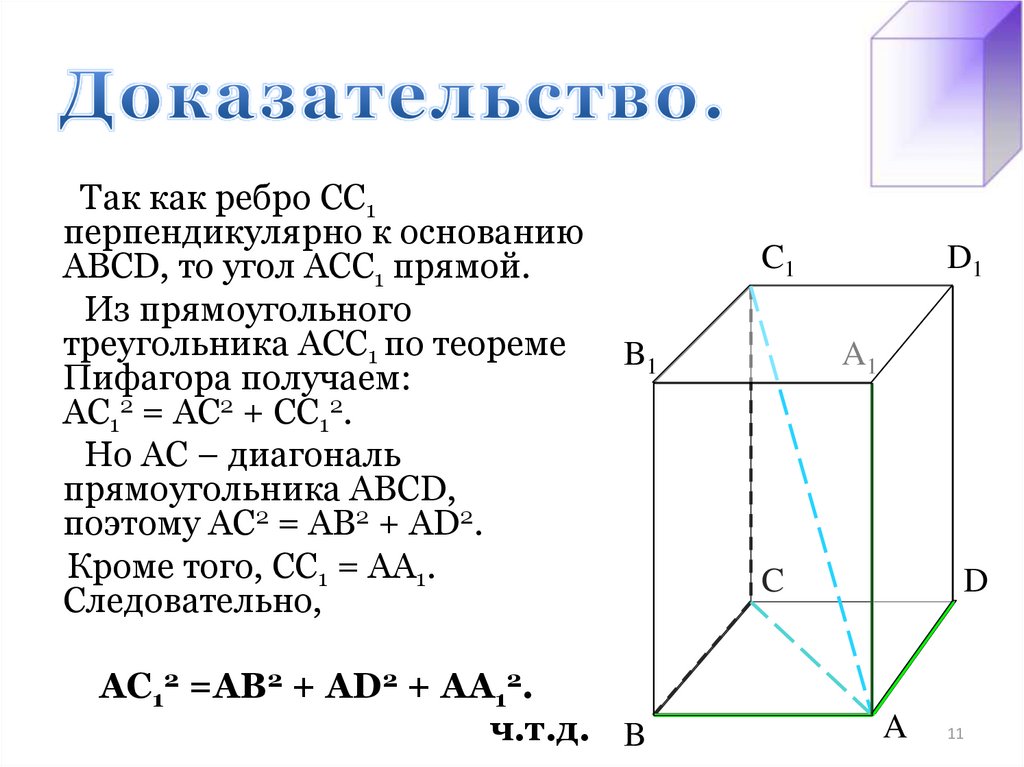
11. Доказательство.

Так как ребро СС1
перпендикулярно к основанию
ABCD, то угол АСС1 прямой.
Из прямоугольного
треугольника АСС1 по теореме
Пифагора получаем:
АС12 = АС2 + СС12.
Но АС – диагональ
прямоугольника ABCD,
поэтому АС2 = АВ2 + AD2.
Кроме того, СС1 = АА1.
Следовательно,
C1
B1
АС12 =АВ2 + AD2 + АА12.
ч.т.д. B
D1
A1
C
D
A
11

12. Следствие

Диагонали
прямоугольного
параллелепипеда
равны.
C1
B1
АС1 = BD1
D1
A1
C
B
D
A
12

13. Куб

Прямоугольный
параллелепипед, у
которого все три
измерения равны,
называется кубом.
Все грани куба –
равные друг другу
квадраты.
B1
A1
C1
D1
B
A
C
D
DA = DC = DD1
13

14.

Задачи на закрепление
Задача № 1. Сколько ушло
проволоки на каркас модели
прямоугольного параллелепипеда,
если его измерения 10 см, 7см и 5 см?
(88 см)
Задача № 2. Высота прямоугольного
параллелепипеда равна 2,4 дм. Длина его
в 3 раза меньше высоты, а ширина в 6 раз
меньше высоты. Найдите площадь
основания прямоугольного
параллелепипеда.
(0,32 дм2)
14

15.

15
Задачи на закрепление

16. Домашнее задание:

• Повторить изученный материал;
• № 187; 188
16

17. д

17

18.

18