Similar presentations:
Прямоугольный параллелепипед
1.
2.
ВИДЫ ПАРАЛЛЕЛЕПИПЕДА3.
D1C1
А1
B1
С
D
А
Наклонный параллелепипед
В
Геометрическое тело или
многогранник, состоящий из
трёх пар равных
параллелограммов лежащих
в параллельных плоскостях,
называется
параллелепипедом
(Назвать вершины, рёбра, грани и их количество.)
4.
ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕДПараллелепипед,
у которого боковые
стороны перпендикулярны основанию,
называется прямым.
5.
ПРЯМОУГОЛЬНЫЙПАРАЛЛЕЛЕПИПЕД
Параллелепипед называется прямоугольным, если его боковые рёбра перпендикулярны к основанию, а основания являются прямоугольниками.
6.
ПРАВИЛЬНЫЙПАРАЛЛЕЛЕПИПЕД
Прямоугольный
параллелепипед,
у которого все
ребра равны,
называется
правильным
7.
C1D1
B1
A1
D
А
С
В
1. В прямоугольном параллелепипеде
все шесть граней – прямоугольники
8.
C1D1
B1
A1
D
А
С
В
2. Все двугранные углы прямоугольного параллелепипеда – прямые.
9.
C1D1
B1
A1
D
А
С
В
3. Диагонали прямоугольного
параллелепипеда равны.
10.
C1D1
B1
A1
D
А
Квадрат
диагонали
равен сумме
квадратов
трех
измерений
С
В
AC1 2=AB2+AD2+AA12
11.
C1D1
B1
A1
D
А
С
В
Sб.п. = Р(осн)∙АА1
12.
C1D1
B1
A1
D
А
С
В
Sп.п. = Sб.п. + 2S(осн)
Sп.п. = Р(осн)∙АА1 + 2S(осн)
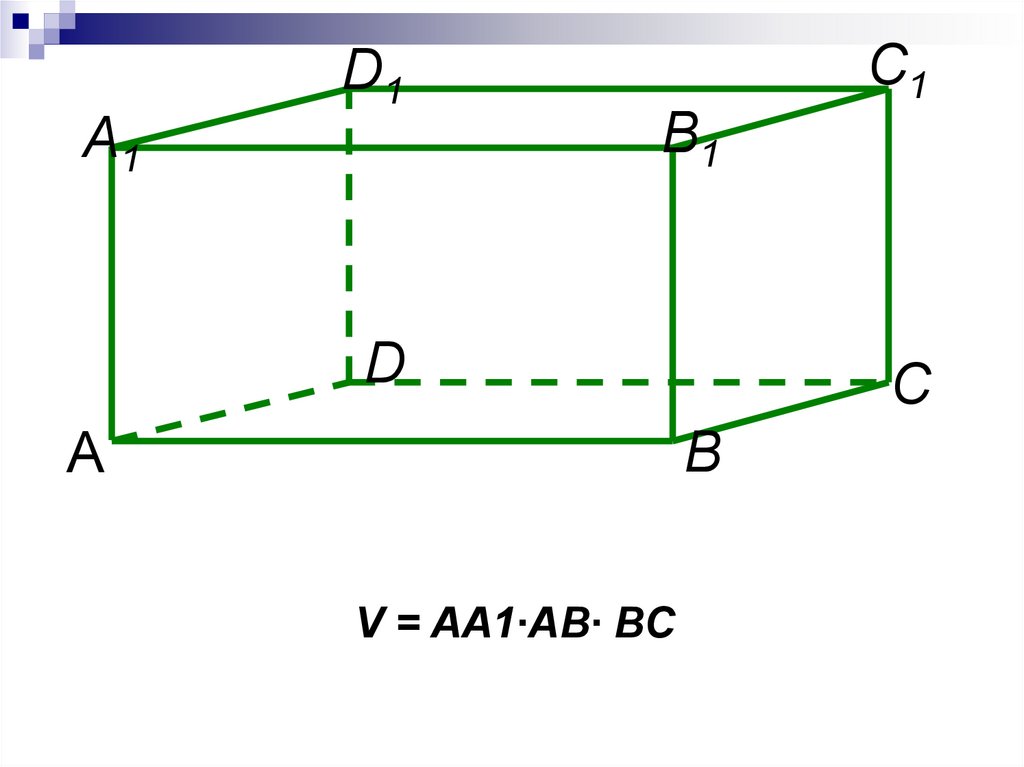
13.
C1D1
B1
A1
D
С
В
А
V = AA1∙AB∙ BC
14.
ЗадачаИзмерения прямоугольного параллелепипеда равны 14, 5 и 10 см.
Вычислить площадь боковой
поверхности параллелепипеда.
15.
Д1А1
Д
А
С1
Дано : АВСДА1В1С1Д1 –прямоугольный
параллелепипед
В1
АА1 ┴ (АВС)
АВ = 14 см
ВС = 5 см
С АА1 = 10 см
Найти: Sб.п.
В
Решение
Sб.п. = Р(осн)∙ АА1
Sб.п. = (14+5+14+5)∙10 = 380 см2
Ответ: Sб.п. = 380 см2
16.
ЗадачаИзмерения прямоугольного параллелепипеда равны 4, 5 и 7 см.
Вычислить площадь полной поверхности параллелепипеда.
17.
Д1А1
Д
А
С1
Дано : АВСДА1В1С1Д1 –прямоугольный
параллелепипед
В1
АА1 ┴ (АВС)
АВ = 4 см
ВС = 5 см
С АА1 = 7 см
Найти: Sп.п.
В
Решение
Sп.п. = S б.п. + 2 S(осн)
Sп.п. = (4+5+4+5)∙7 + 2∙4∙5 = 18∙7 + 40 =
=126 + 40 = 166 см2
Ответ: Sп.п. = 166 см2
18.
Даны измерения параллелепипеда:4 см, 5 см, 13 см
32 м, 18 м, 52 м
3,7 дм, 6,9 дм, 4,8 дм
2,42 см, 4,06 см, 7,32 см
0,542 мм, 2,864 мм, 6,071 мм
Найдите площади поверхностей параллелепипедов

















 mathematics
mathematics