Прямоугольный параллелепипед

1.

Кто ничего не замечает
Тот ничего не изучает
Кто ничего не изучает
Тот вечно хнычет и скучает.

2.

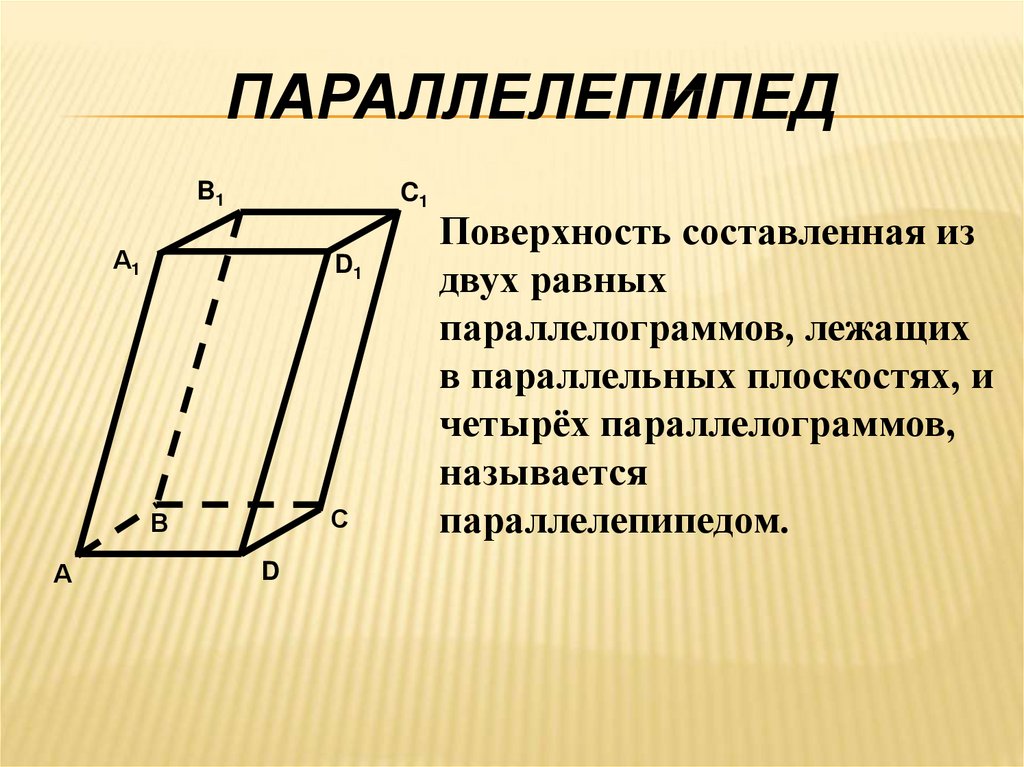
ПАРАЛЛЕЛЕПИПЕД
B1
C1
А1
D1
С
В
А
D
Поверхность составленная из
двух равных
параллелограммов, лежащих
в параллельных плоскостях, и
четырёх параллелограммов,
называется
параллелепипедом.

3.

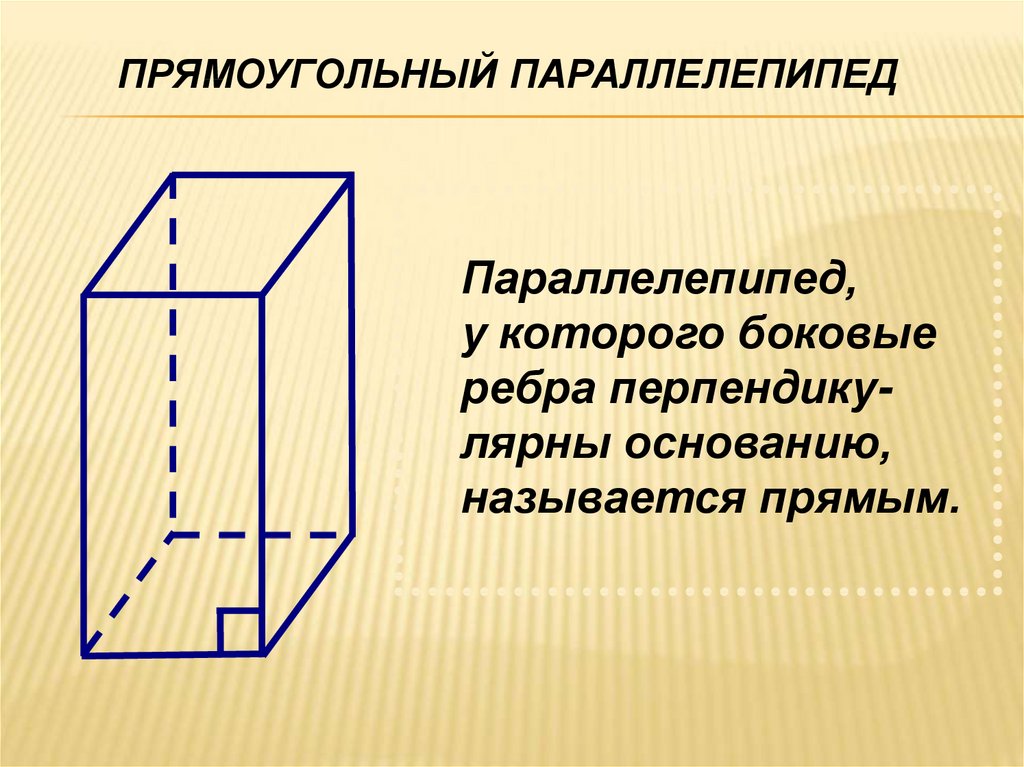
ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
Параллелепипед,
у которого боковые
ребра перпендикулярны основанию,
называется прямым.

4.

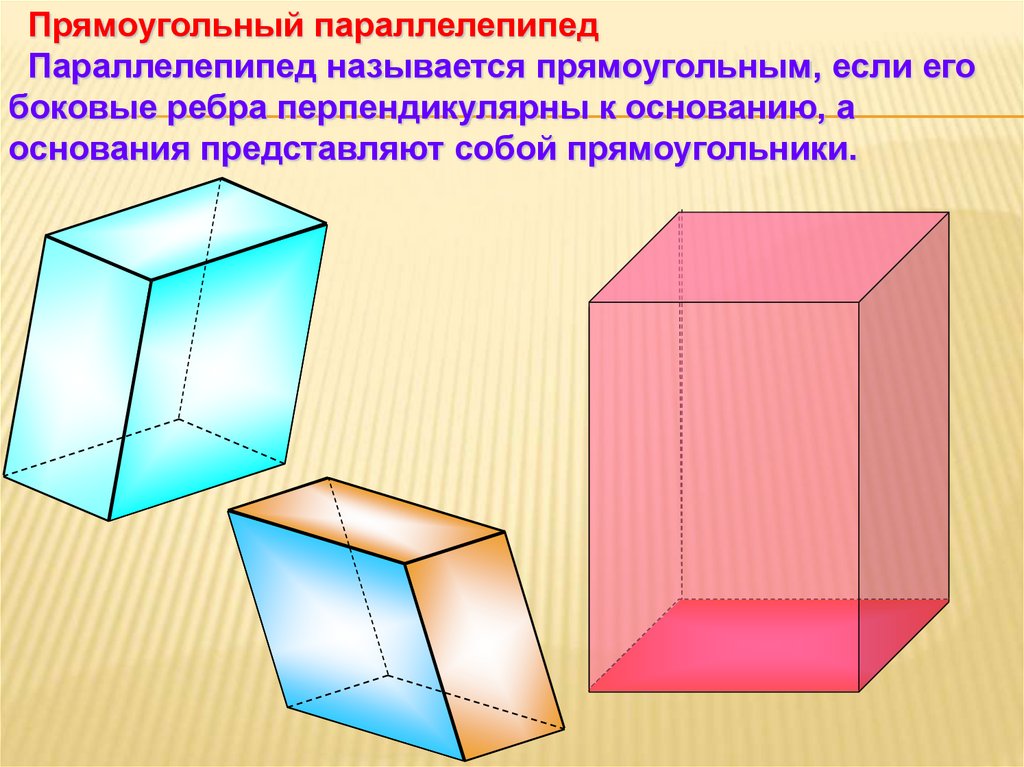
Прямоугольный параллелепипед
Параллелепипед называется прямоугольным, если его
боковые ребра перпендикулярны к основанию, а
основания представляют собой прямоугольники.

5.

Д1
С1
А1
В1
Д
А
С
В
10. В прямоугольном
параллелепипеде
все шесть граней –
прямоугольники.
20. Все двугранные углы
прямоугольного
параллелепипеда –
прямые.

6.

Длины трех ребер, имеющих
общую вершину, называются
измерениями прямоугольного
параллелепипеда
с
в
а

7.

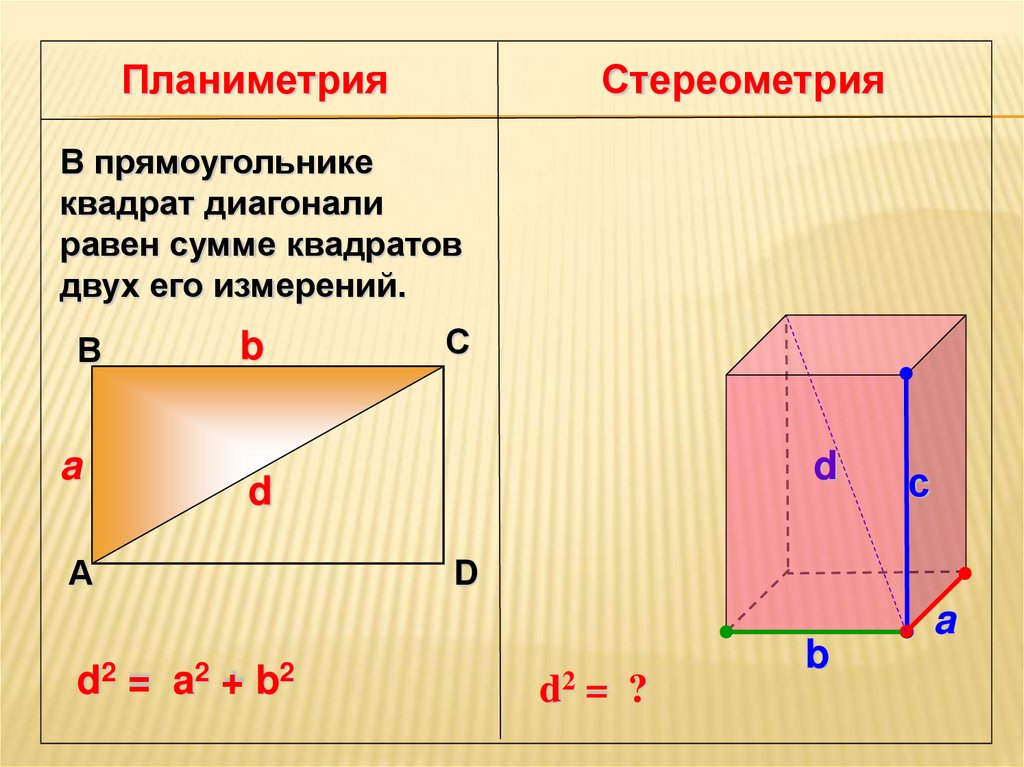
Планиметрия
Стереометрия
В прямоугольнике
квадрат диагонали
равен сумме квадратов
двух его измерений.
b
В
a
d
d
А
d2
С
с
D
=
a2
+
b2
d2 = ?
b
a

8.

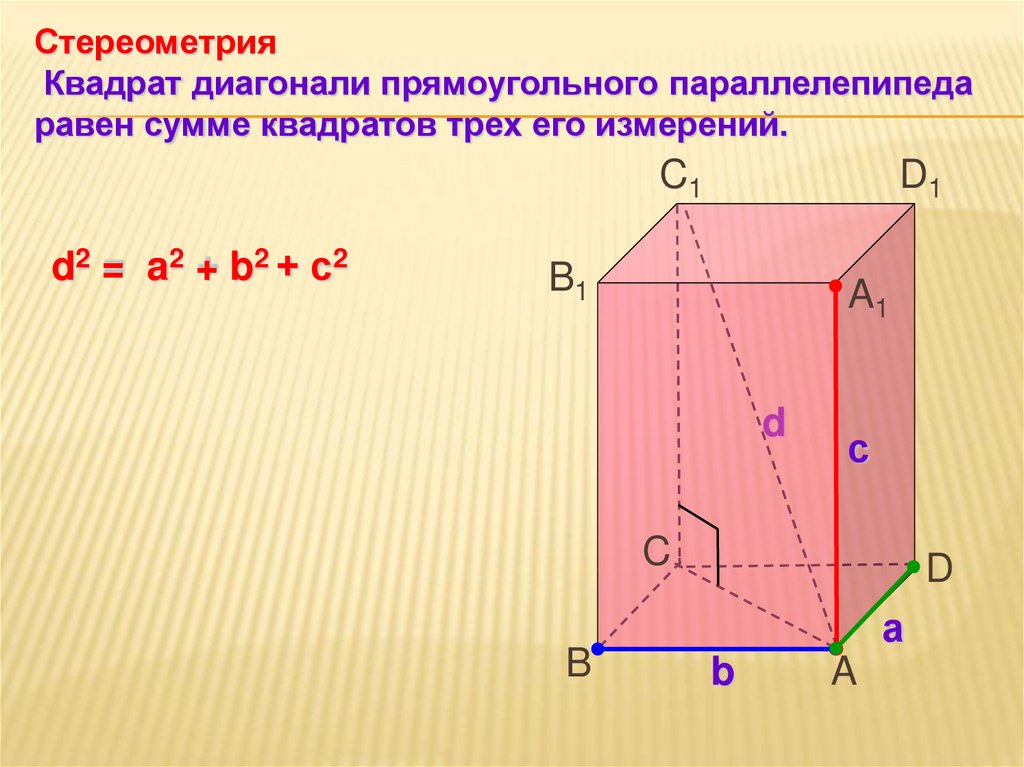
Стереометрия
Квадрат диагонали прямоугольного параллелепипеда
равен сумме квадратов трех его измерений.
C1
d2 = a2 + b2 + с2
D1
B1
A1
d
с
C
B
D
а
b
A

9.

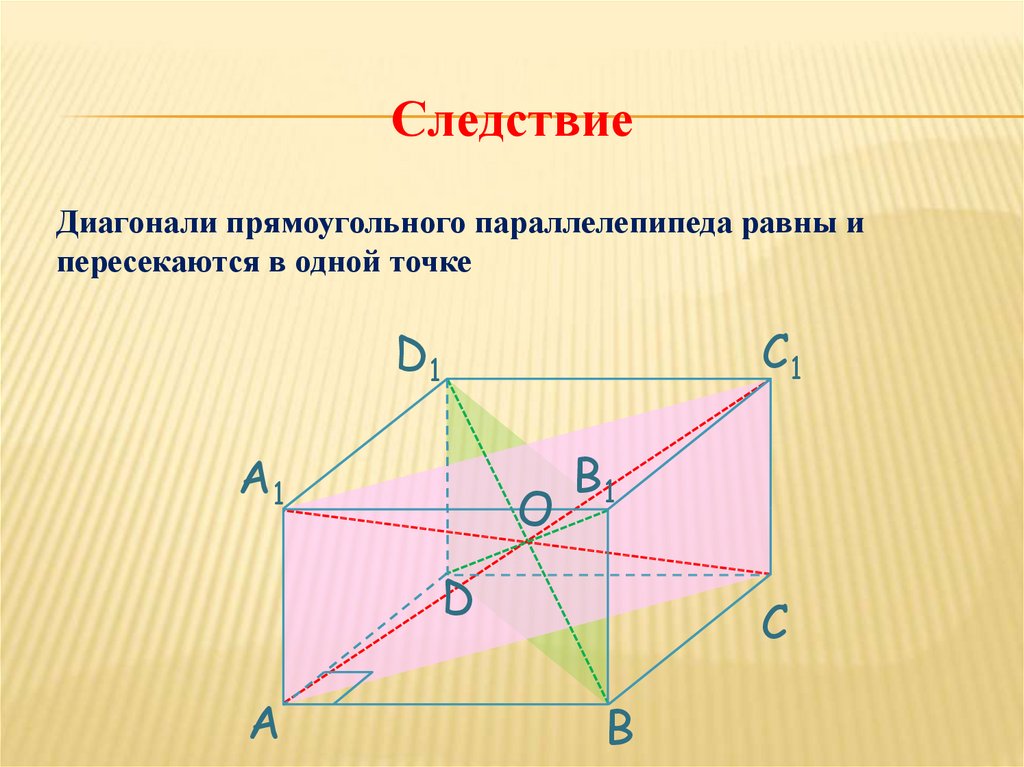
Следствие
Диагонали прямоугольного параллелепипеда равны и
пересекаются в одной точке
C1
D1
А1
О
B1
D
А
C
B

10.

Задача.
Найти диагональ прямоугольного параллелепипеда:
1.
a=2, b=4, c=4, d=?
2. a=7, b=6, c=5, d= ?
d
c
b
a
3. a=3, b=7, c=4, d=?

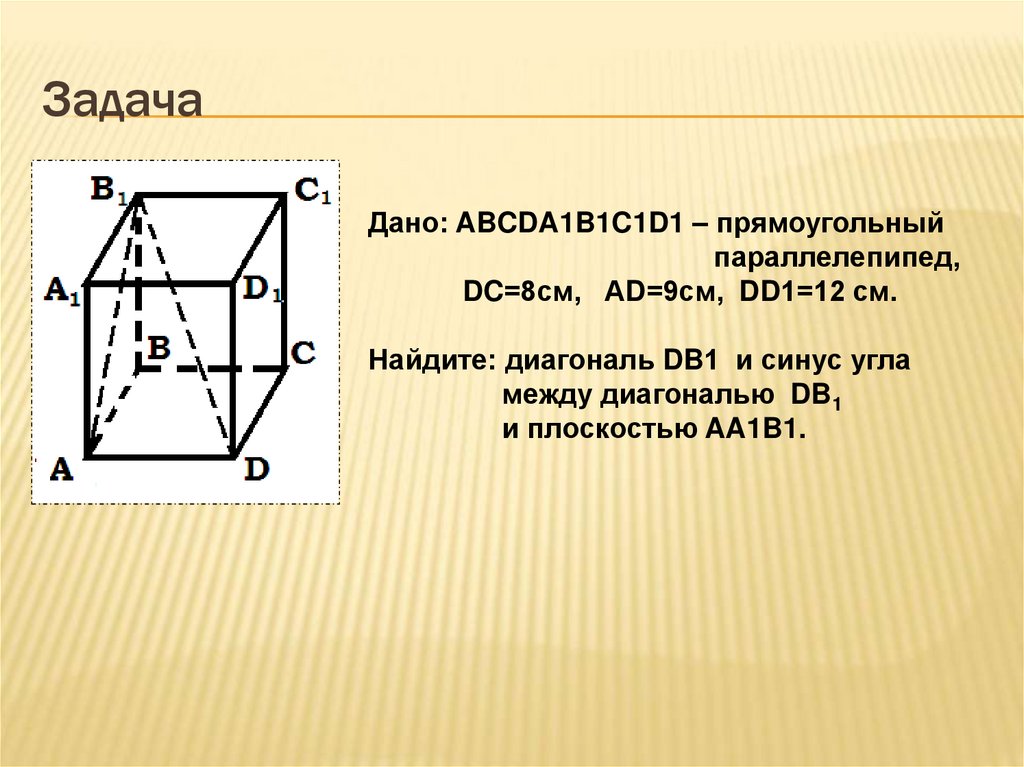
11. Задача

Дано: ABCDA1B1C1D1 – прямоугольный
параллелепипед,
DC=8см, АD=9см, DD1=12 см.
Найдите: диагональ DB1 и синус угла
между диагональю DB1
и плоскостью AA1B1.

12.

ПРАВИЛЬНЫЙ
ПАРАЛЛЕЛЕПИПЕД
КУБ

13.

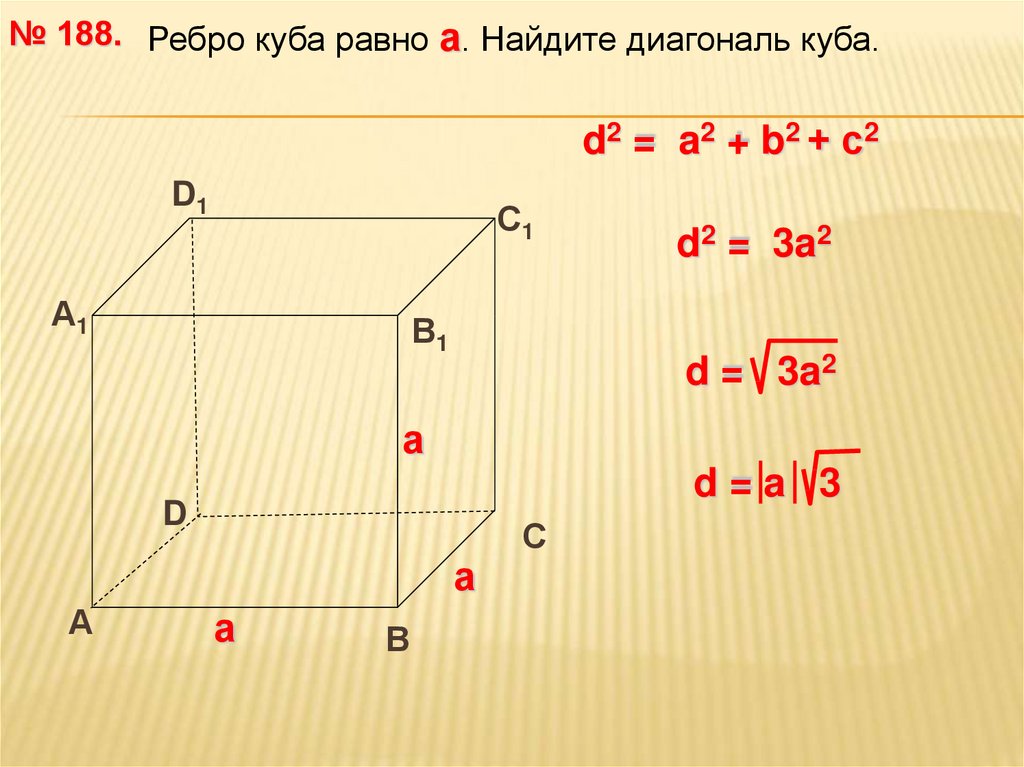
№ 188. Ребро куба равно а. Найдите диагональ куба.
d2 = a2 + b2 + с2
D1
С1
А1
В1
d2 = 3a2
d = 3a2
а
d=a 3
D
а
А
а
В
С

14.

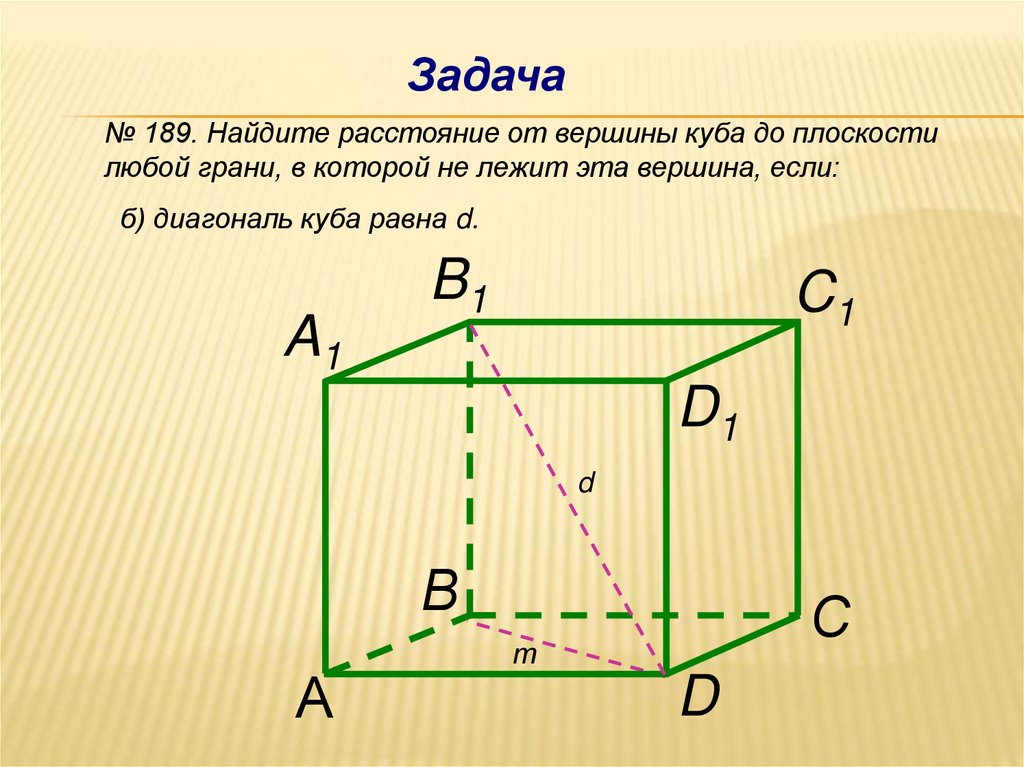
Задача
№ 189. Найдите расстояние от вершины куба до плоскости
любой грани, в которой не лежит эта вершина, если:
б) диагональ куба равна d.
A1
B1
C1
D1
d
В
А
С
т
D

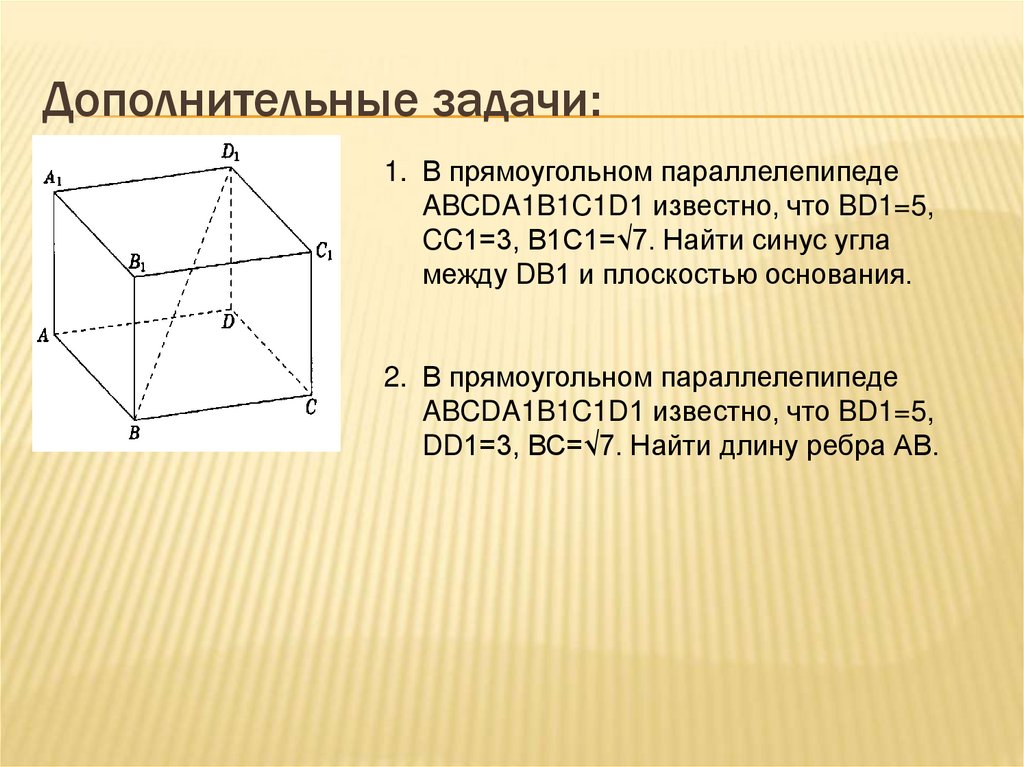
15. Дополнительные задачи:

1. В прямоугольном параллелепипеде
ABCDA1B1C1D1 известно, что BD1=5,
CC1=3, В1С1=√7. Найти синус угла
между DB1 и плоскостью основания.
2. В прямоугольном параллелепипеде
ABCDA1B1C1D1 известно, что BD1=5,
DD1=3, ВС=√7. Найти длину ребра АВ.