Similar presentations:
Прямоугольный параллелепипед
1. 13. 01. ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
2.
3. Определение:
Двугранным углом называетсяфигура, образованная …
4.
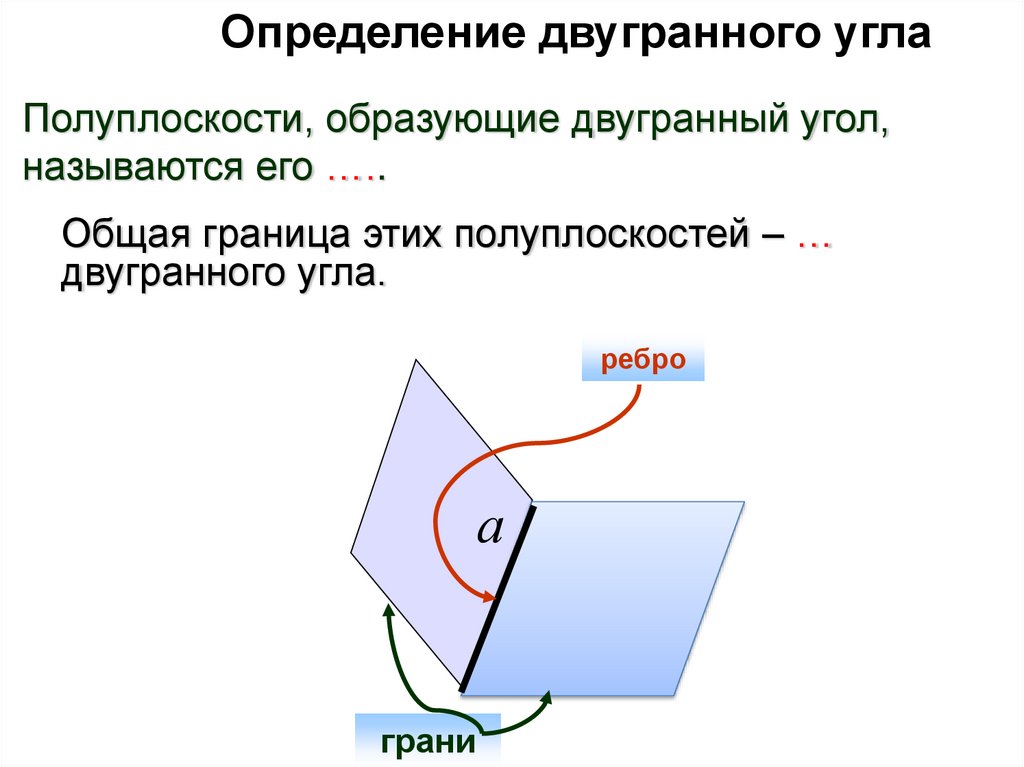
Определение двугранного угла.
Полуплоскости,
образующие двугранный угол,
называются его …..
Общая граница этих полуплоскостей – …
двугранного угла.
ребро
а
грани
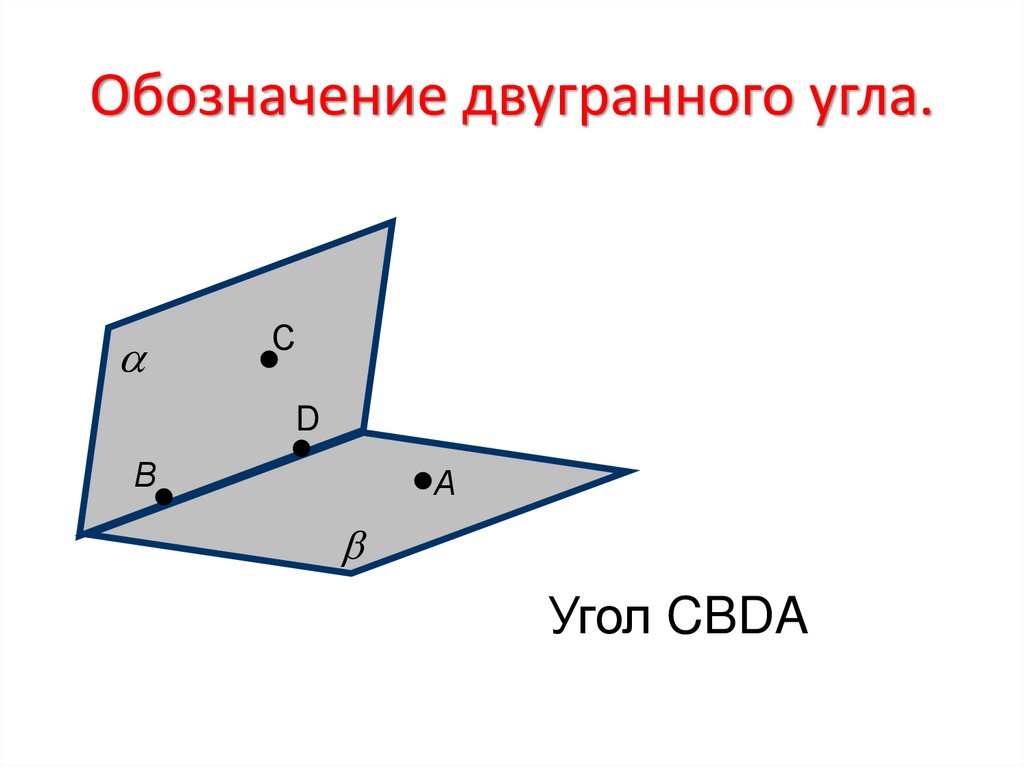
5. Обозначение двугранного угла.
СD
В
А
Угол CBDA
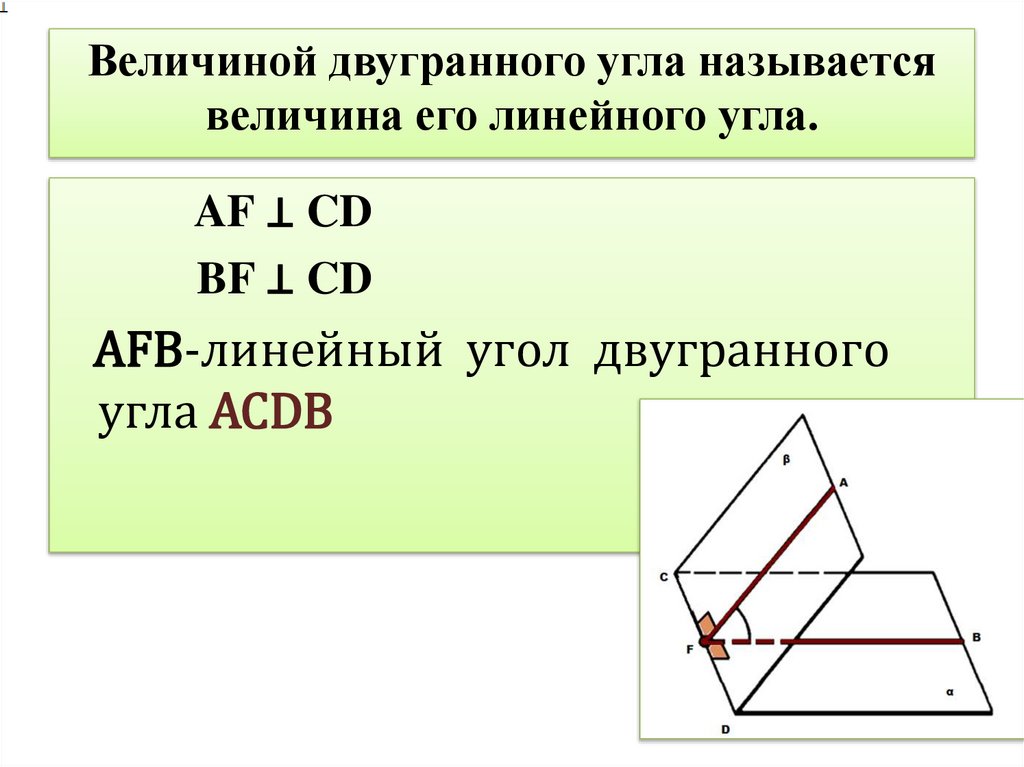
6. Величиной двугранного угла называется величина его линейного угла.
AF ⊥ CDBF ⊥ CD
AFB-линейный угол двугранного
угла ACDВ
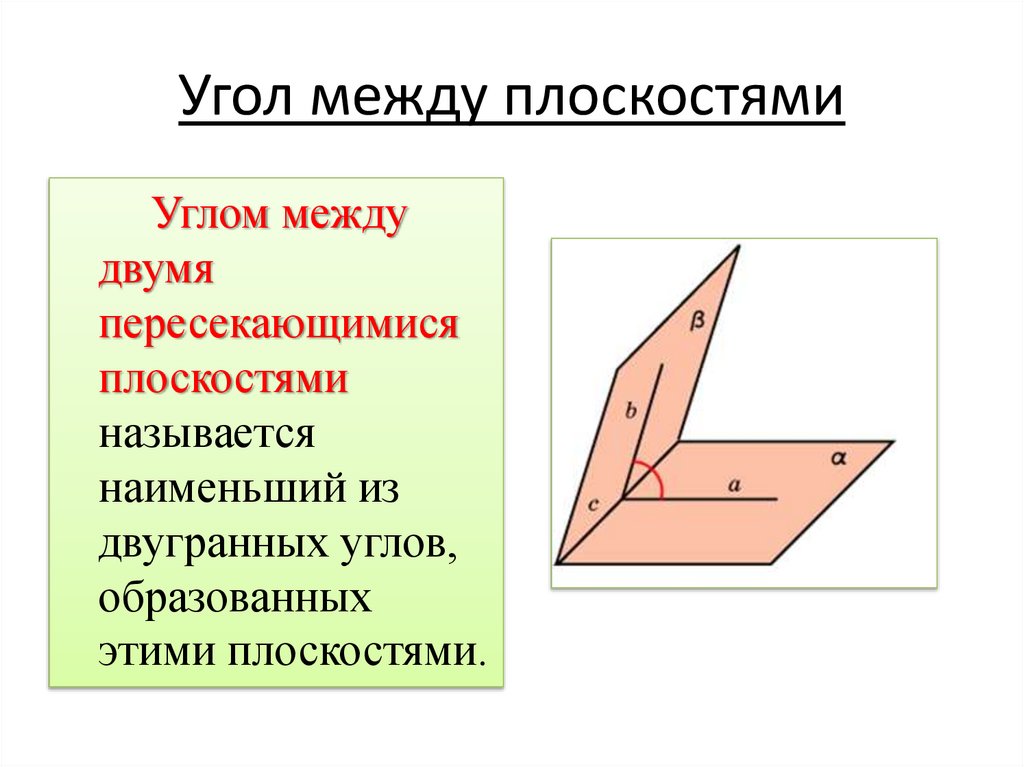
7. Угол между плоскостями
Углом междудвумя
пересекающимися
плоскостями
называется
наименьший из
двугранных углов,
образованных
этими плоскостями.
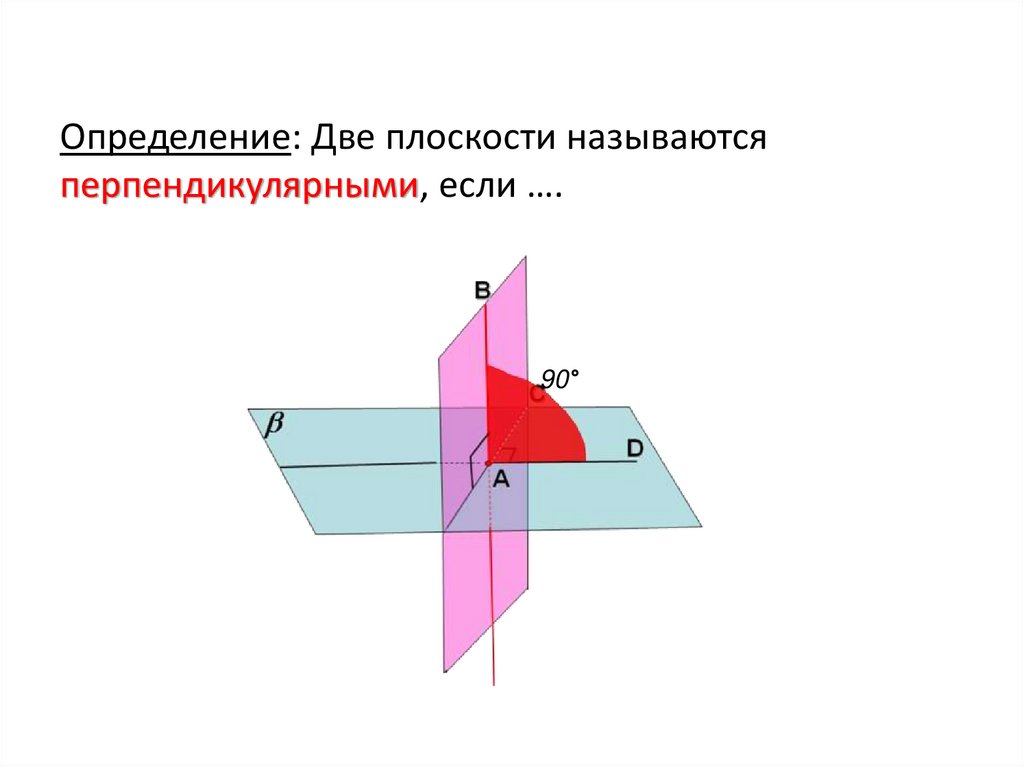
8. Определение: Две плоскости называются перпендикулярными, если ….
90°9.
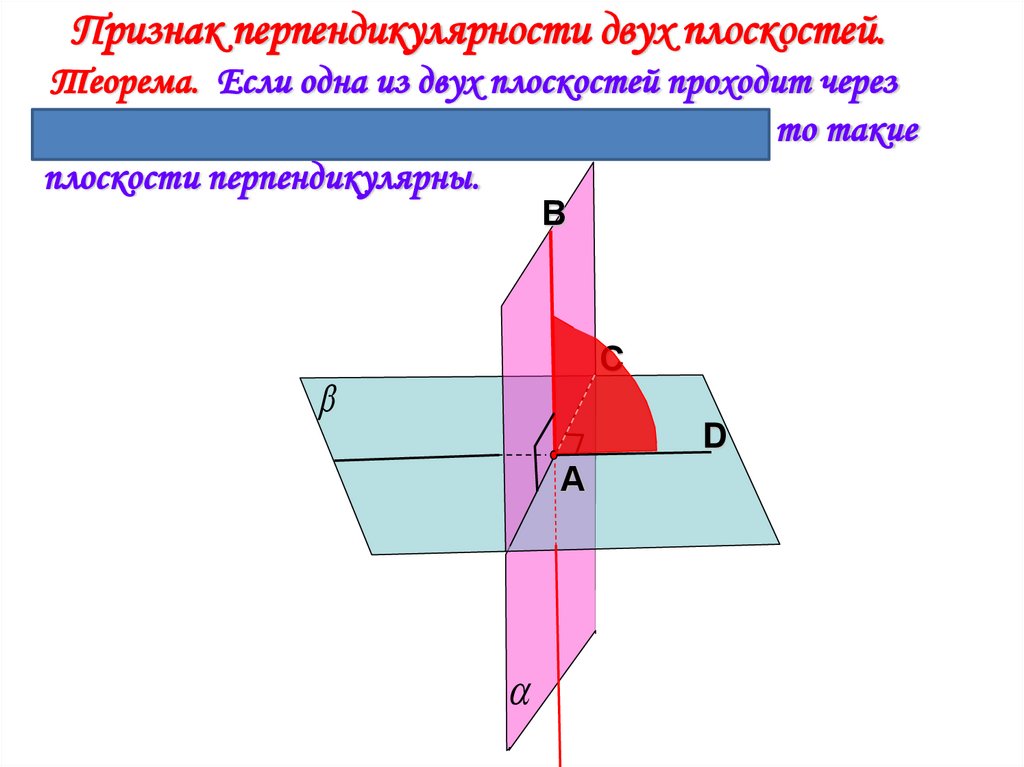
Признак перпендикулярности двух плоскостей.Теорема. Если одна из двух плоскостей проходит через
прямую, перпендикулярную к другой плоскости, то такие
плоскости перпендикулярны.
В
С
D
А
10.
11.
№ 174.Дано:
Найти:
Признак перпендикулярности двух плоскостей.
Теорема. Если одна из двух плоскостей проходит через
прямую, перпендикулярную к другой плоскости, то такие
плоскости перпендикулярны.
12.
13.
14.
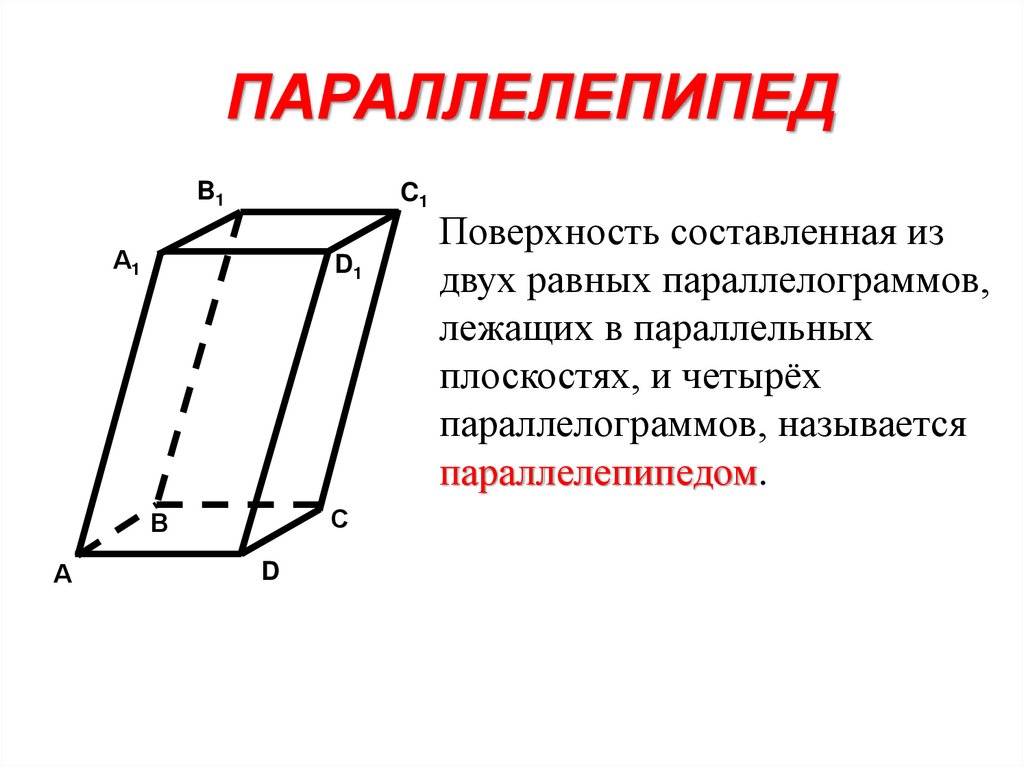
ПАРАЛЛЕЛЕПИПЕДB1
C1
А1
D1
С
В
А
D
Поверхность составленная из
двух равных параллелограммов,
лежащих в параллельных
плоскостях, и четырёх
параллелограммов, называется
параллелепипедом.
15.
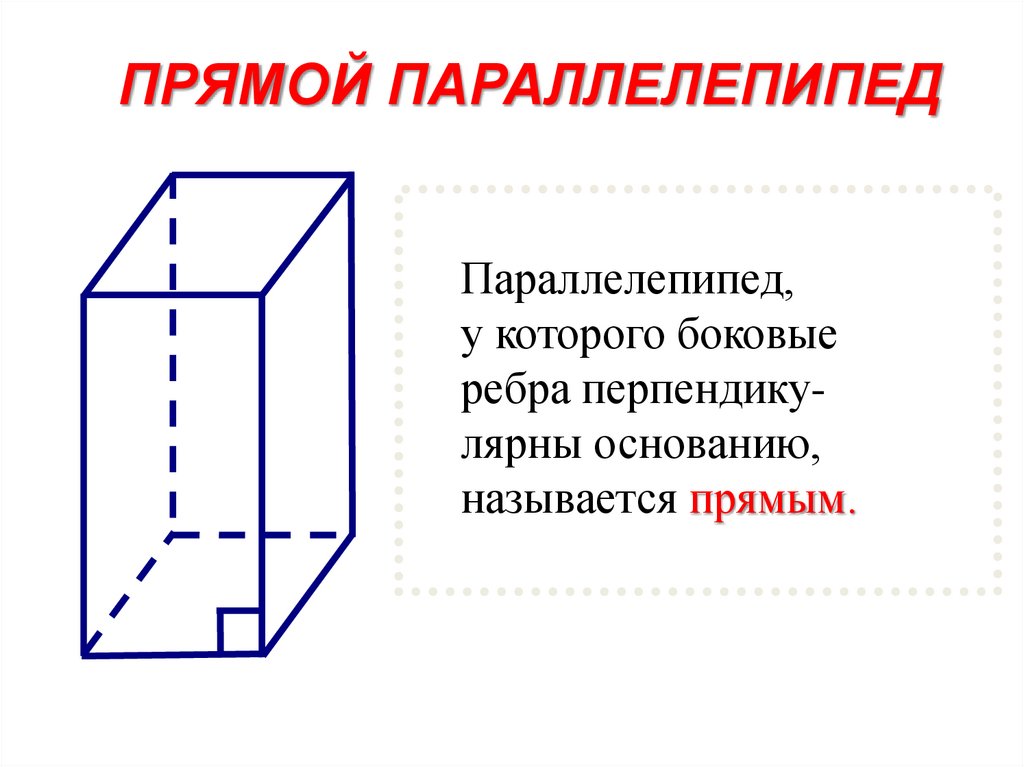
ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕДПараллелепипед,
у которого боковые
ребра перпендикулярны основанию,
называется прямым.
16.
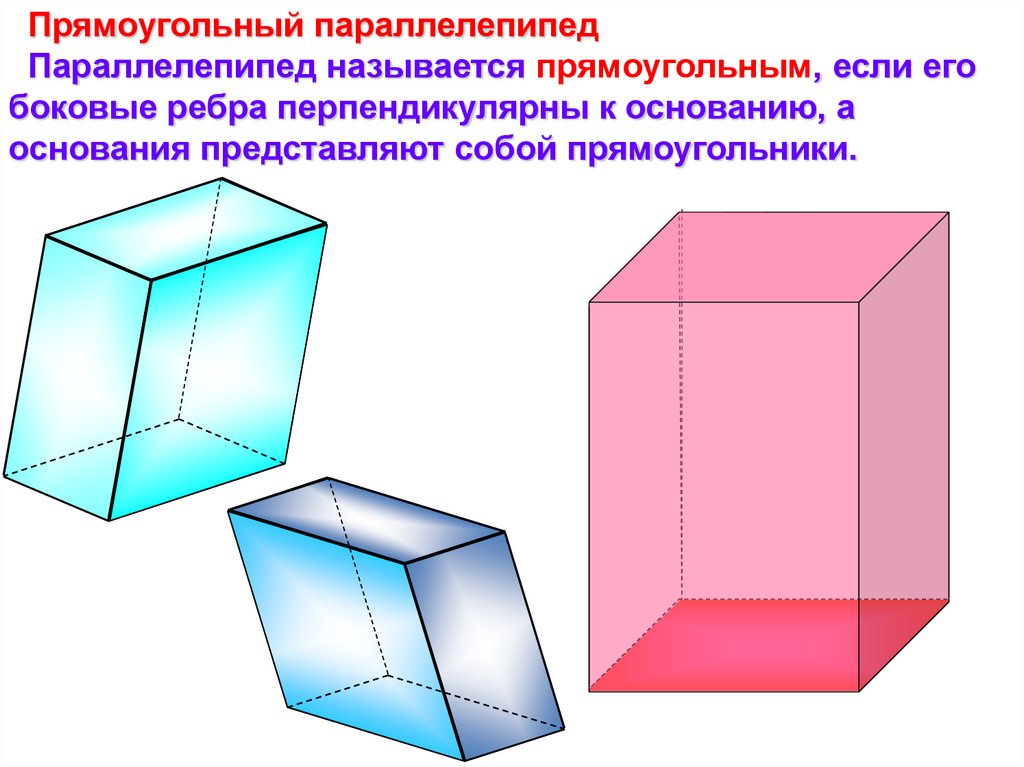
Прямоугольный параллелепипедПараллелепипед называется прямоугольным, если его
боковые ребра перпендикулярны к основанию, а
основания представляют собой прямоугольники.
17.
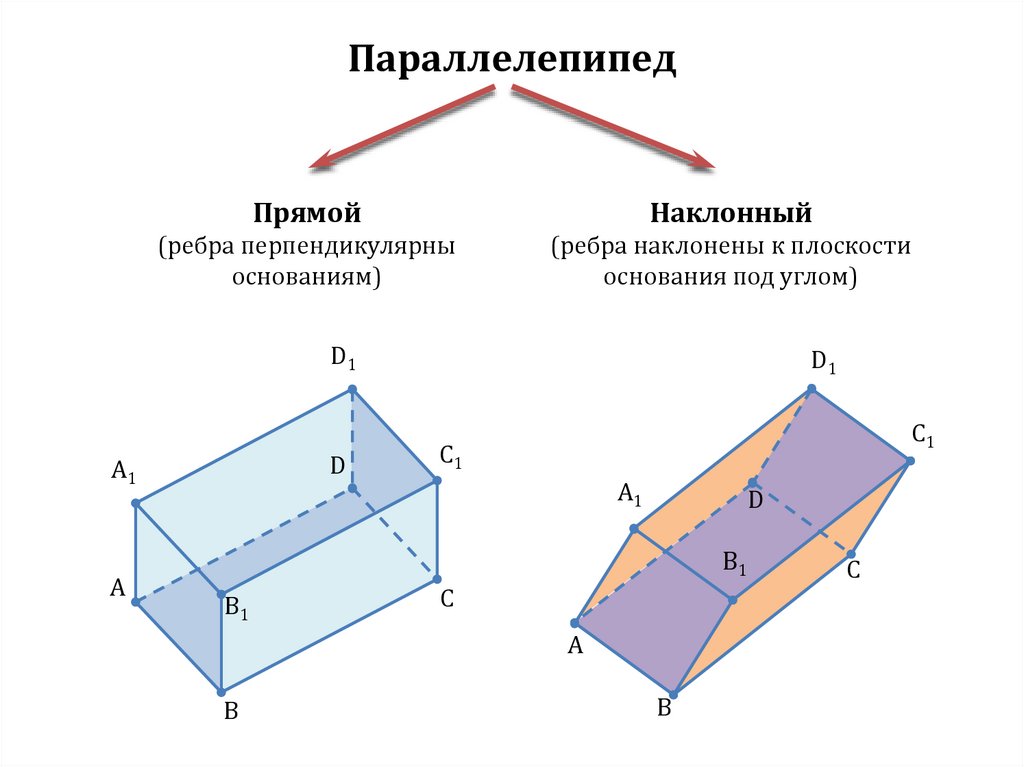
ПараллелепипедПрямой
Наклонный
(ребра перпендикулярны
основаниям)
(ребра наклонены к плоскости
основания под углом)
D1
D
A1
A
D1
C1
C1
A1
D
B1
B1
C
A
B
B
C
18.
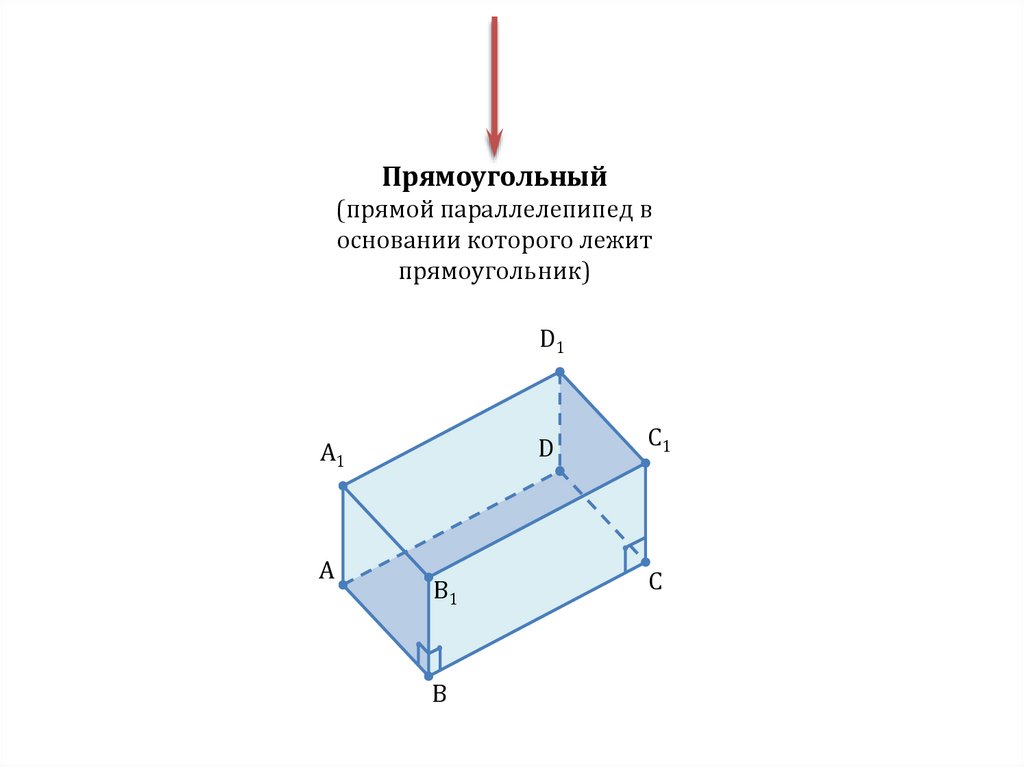
Прямоугольный(прямой параллелепипед в
основании которого лежит
прямоугольник)
D1
D
A1
A
B1
B
C1
C
19.
Системный блокКниги
Микроволновая печь
20.
Прямоугольныйпараллелепипед
21.
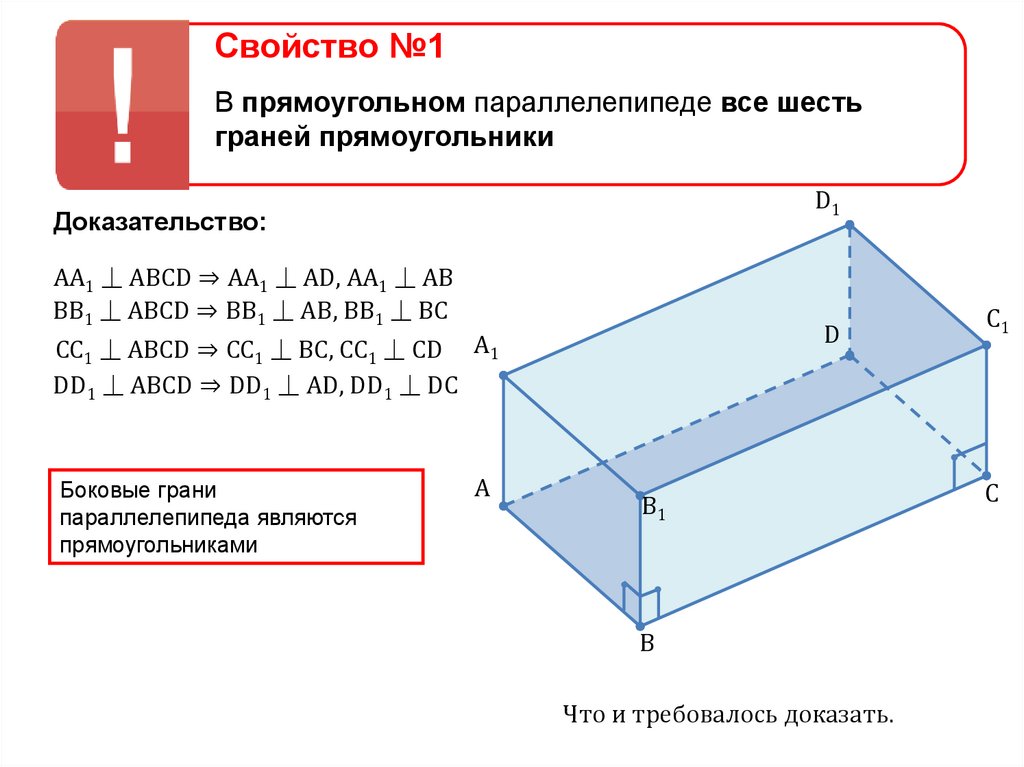
Свойство №1В прямоугольном параллелепипеде все шесть
граней прямоугольники
D1
Доказательство:
AA1 ⏊ ABCD ⇒ AA1 ⏊ AD, AA1 ⏊ AB
BB1 ⏊ ABCD ⇒ BB1 ⏊ AB, BB1 ⏊ BC
D
CC1 ⏊ ABCD ⇒ CC1 ⏊ BC, CC1 ⏊ CD A1
DD1 ⏊ ABCD ⇒ DD1 ⏊ AD, DD1 ⏊ DC
Боковые грани
параллелепипеда являются
прямоугольниками
A
B1
B
Что и требовалось доказать.
C1
C
22.
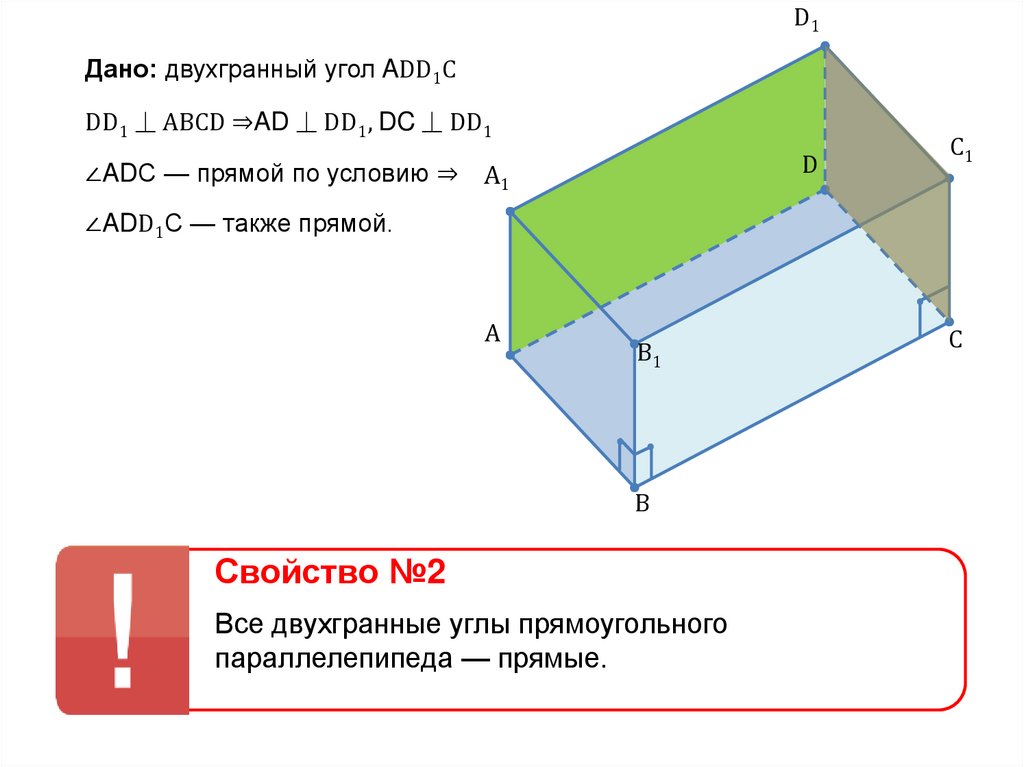
D1Дано: двухгранный угол ADD1C
DD1 ⏊ ABCD ⇒AD ⏊ DD1, DC ⏊ DD1
D
∠ADС — прямой по условию ⇒ A1
C1
∠ADD1С — также прямой.
A
B1
B
Свойство №2
Все двухгранные углы прямоугольного
параллелепипеда — прямые.
C
23.
Д1С1
А1
В1
Д
А
С
В
10. В прямоугольном
параллелепипеде
все шесть граней –
прямоугольники.
20. Все двугранные углы
прямоугольного
параллелепипеда –
прямые.
24.
C1D1
B1
A1
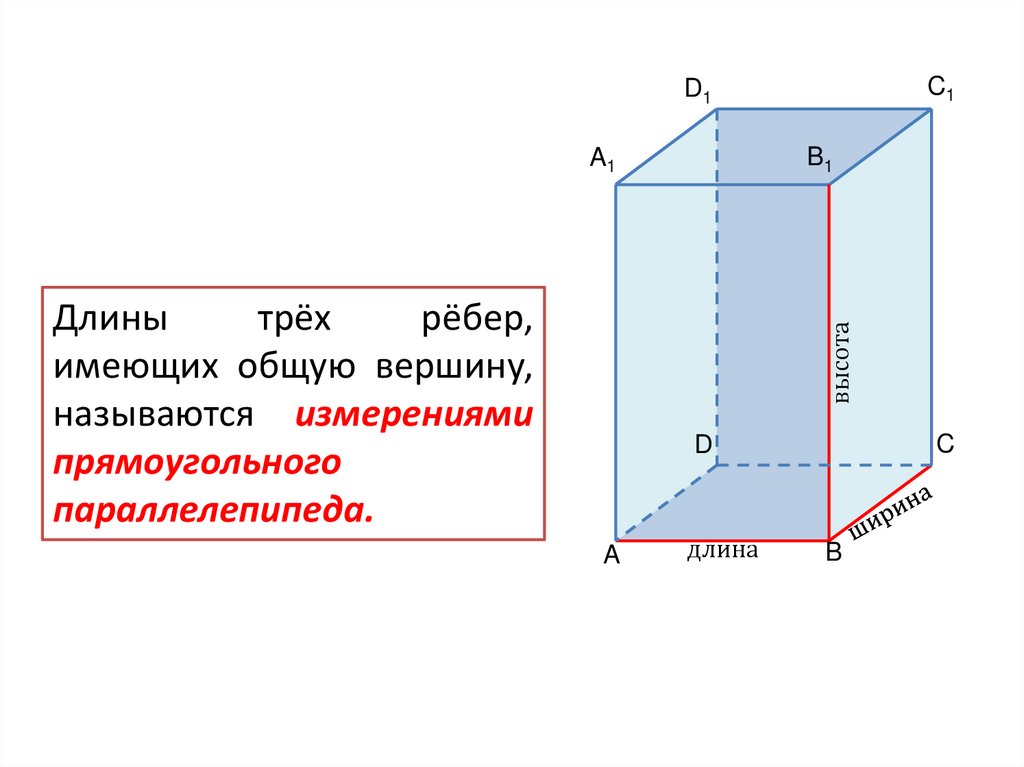
высота
Длины
трёх
рёбер,
имеющих общую вершину,
называются измерениями
прямоугольного
параллелепипеда.
C
D
A
длина
B
25.
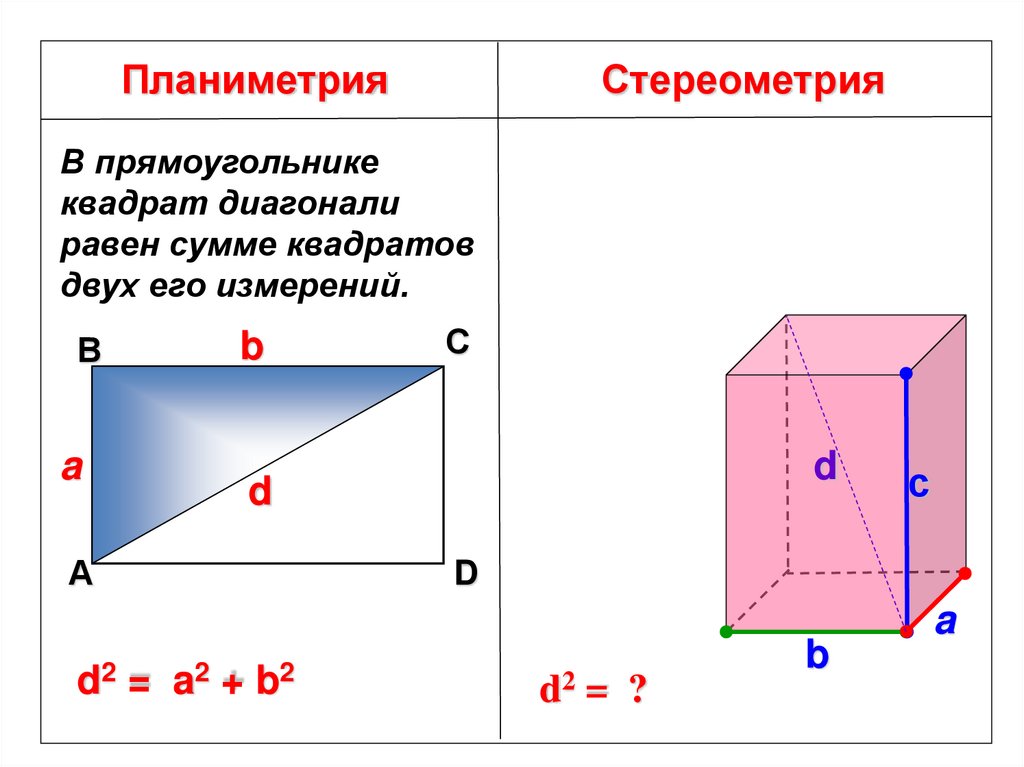
ПланиметрияСтереометрия
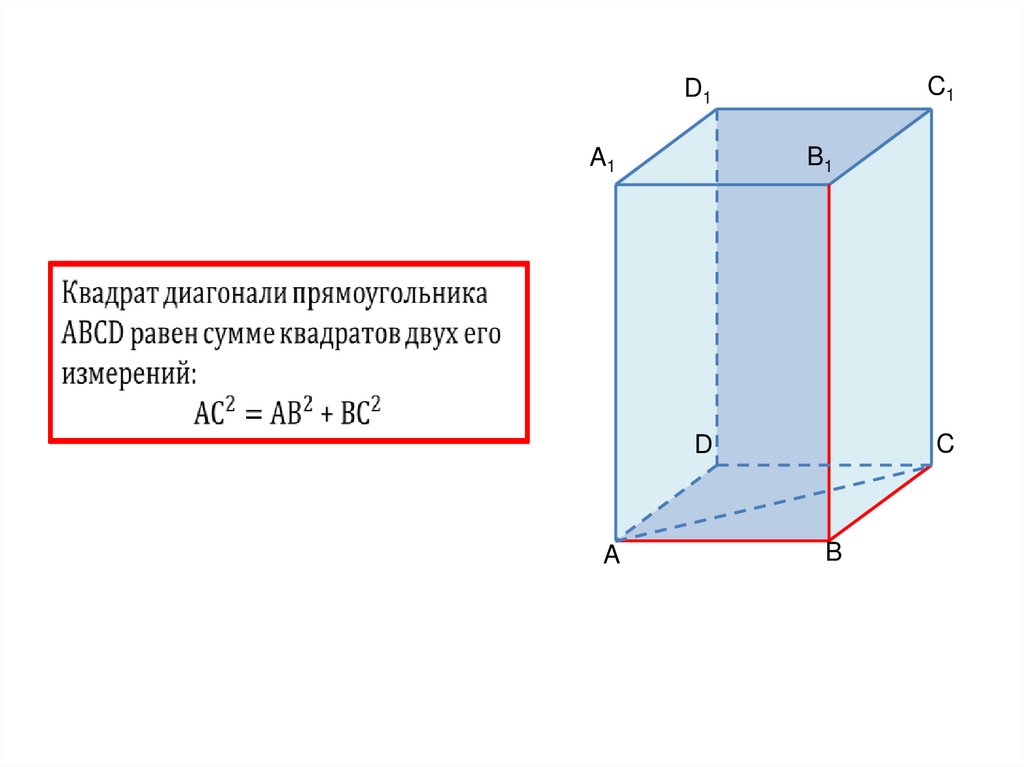
В прямоугольнике
квадрат диагонали
равен сумме квадратов
двух его измерений.
В
a
b
d
d
А
d2 =
С
с
D
a2 + b2
d2 = ?
b
a
26.
C1D1
B1
A1
C
D
A
B
27.
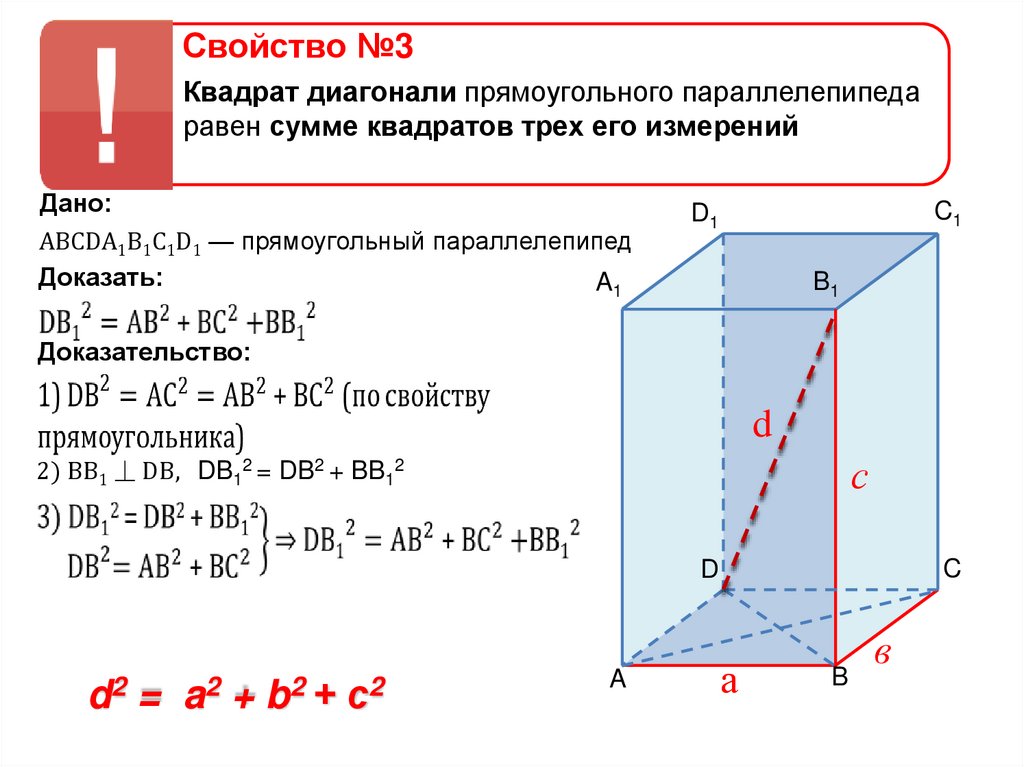
Свойство №3Квадрат диагонали прямоугольного параллелепипеда
равен сумме квадратов трех его измерений
Дано:
ABCDA1B1C1D1 — прямоугольный параллелепипед
Доказать:
A1
C1
D1
B1
Доказательство:
d
с
2) BB1 ⏊ DB, DB12 = DB2 + BB12
C
D
d2 =
a2 + b2 + с2
A
а
B
в
28.
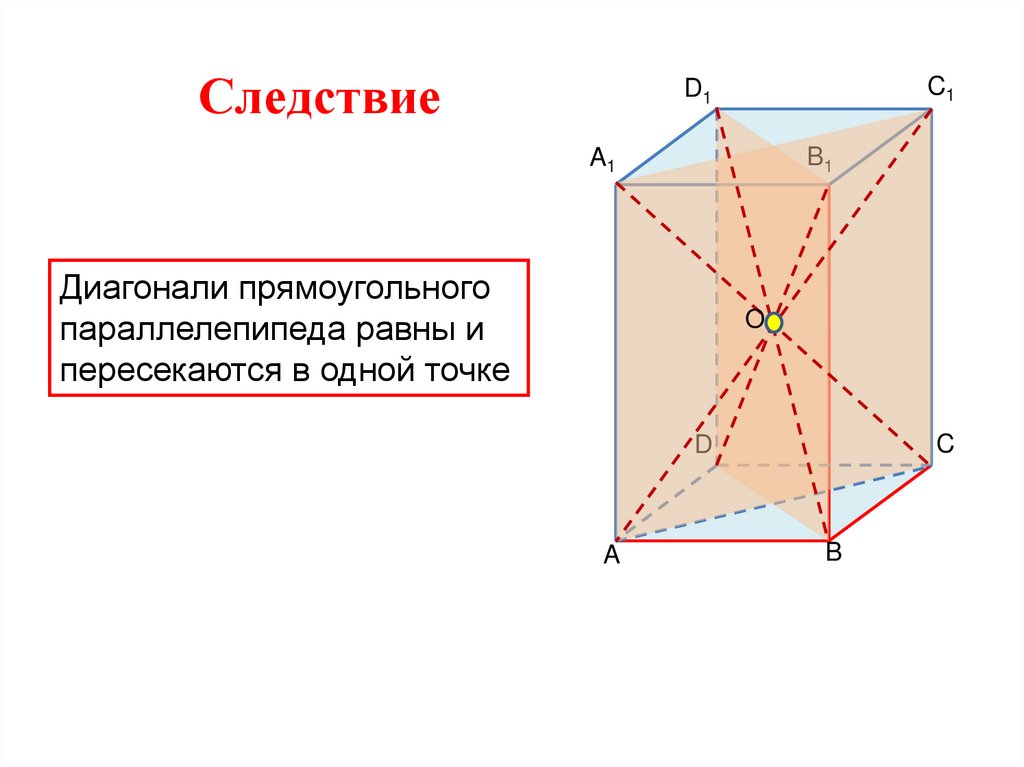
СледствиеC1
D1
B1
A1
Диагонали прямоугольного
параллелепипеда равны и
пересекаются в одной точке
O
C
D
A
B
29.
30.
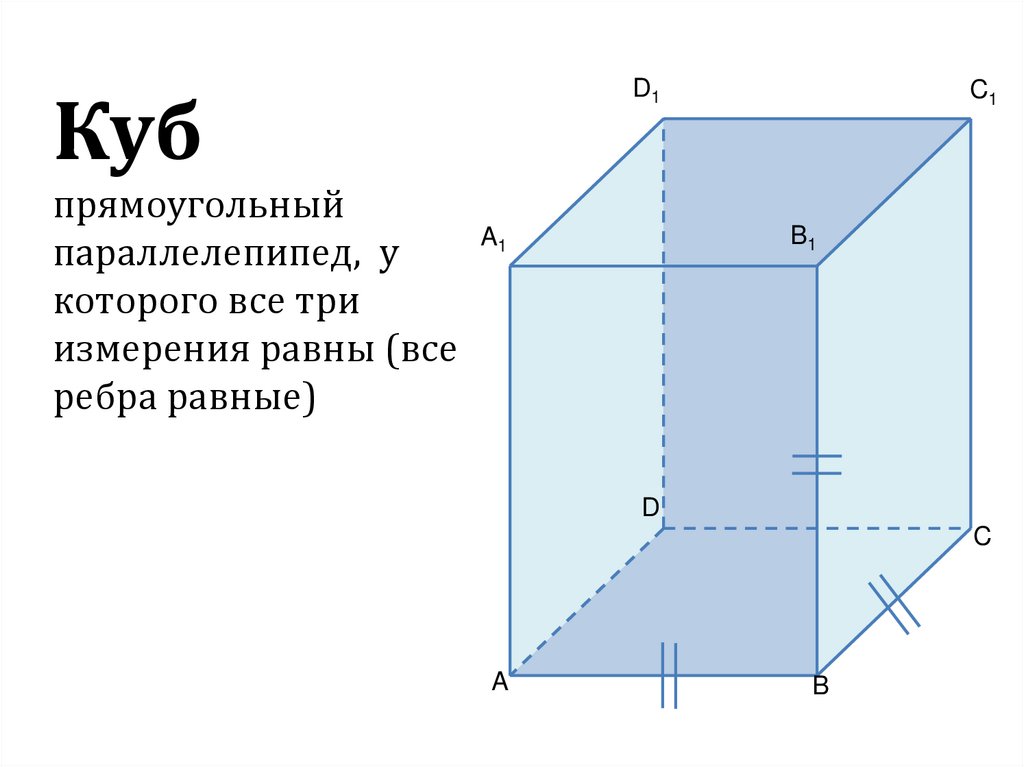
КубD1
прямоугольный
A1
параллелепипед, у
которого все три
измерения равны (все
ребра равные)
C1
B1
D
C
A
B
31.
ПРАВИЛЬНЫЙПАРАЛЛЕЛЕПИПЕД
КУБ
32.
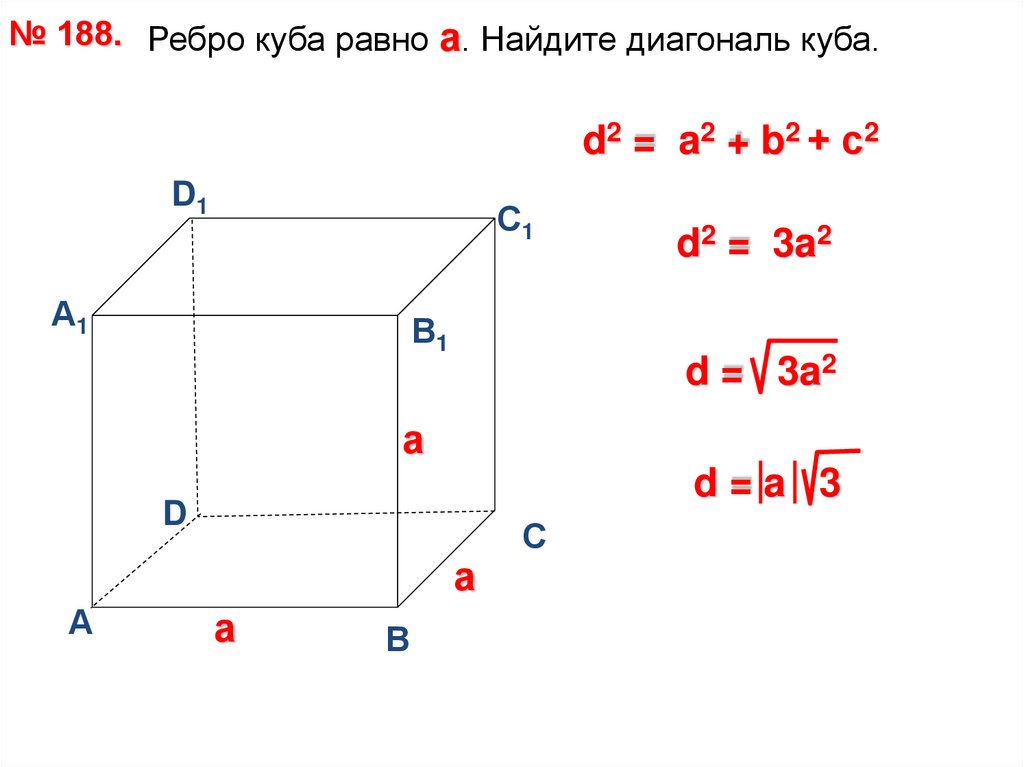
№ 188. Ребро куба равно а. Найдите диагональ куба.d2 = a2 + b2 + с2
D1
С1
А1
В1
d2 = 3a2
d = 3a2
а
d=a 3
D
а
А
а
В
С
33.
A1B1
C1
D1
d
В
А
С
т
D
34.
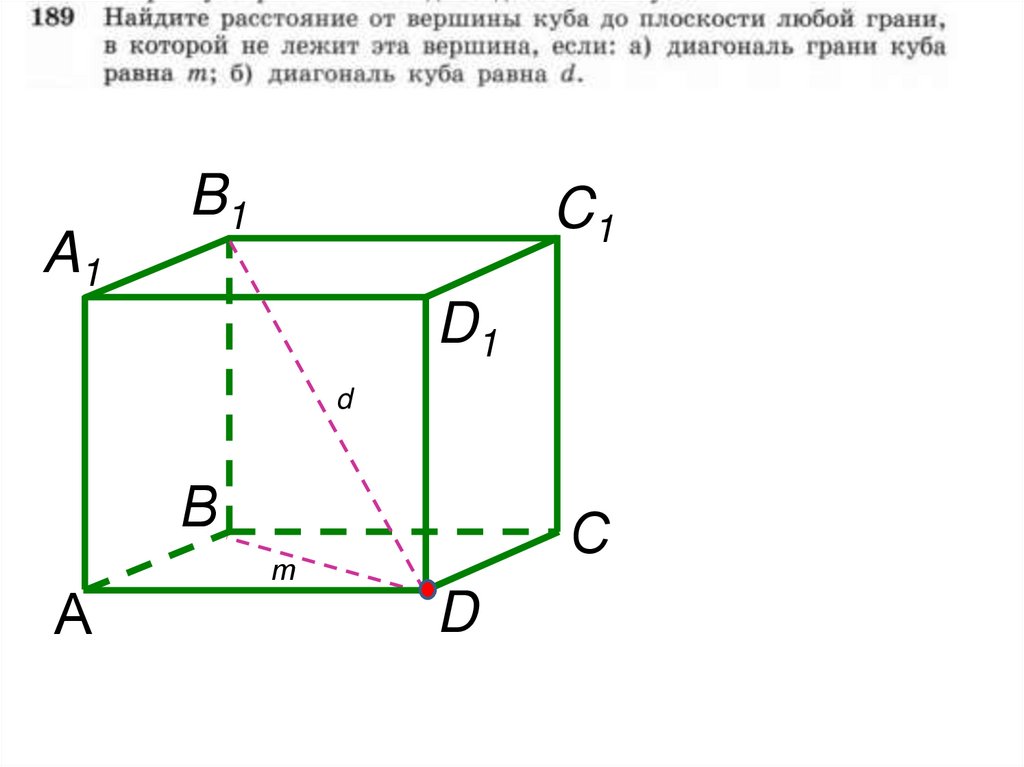
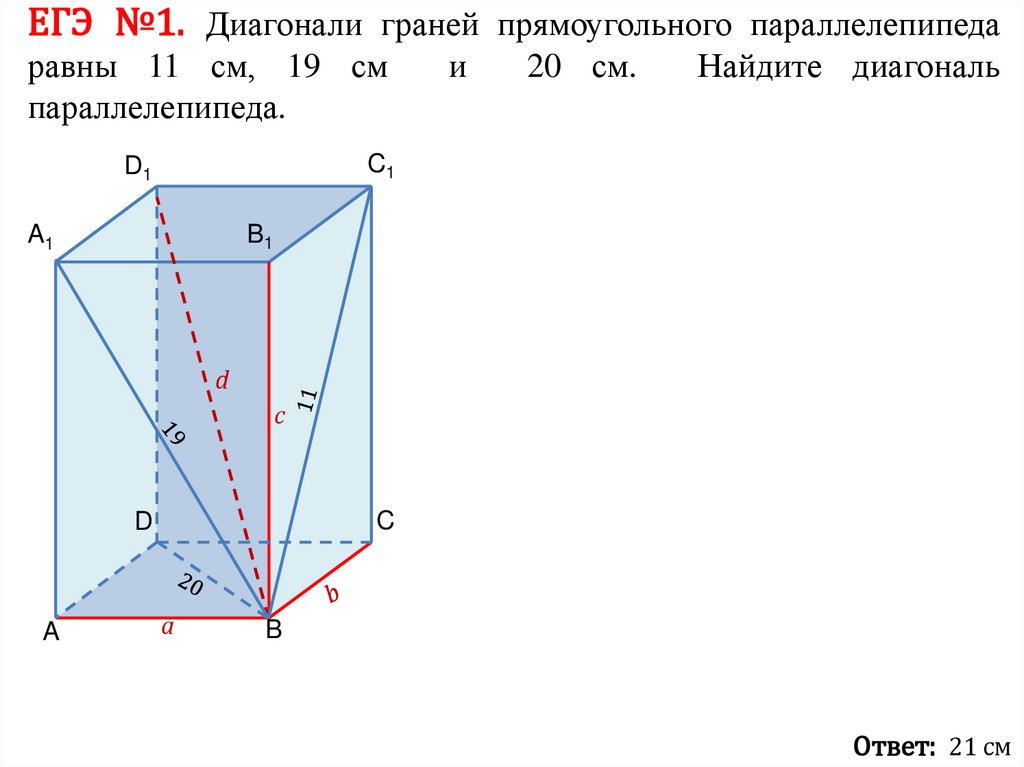
ЕГЭ №1. Диагонали граней прямоугольного параллелепипедаравны 11 см, 19 см
параллелепипеда.
и
20 см.
Найдите диагональ
C1
D1
B1
A1
d
c
C
D
A
a
B
Ответ: 21 см









 mathematics
mathematics








