Тетраэдр и параллелепипед

1. ТЕТРАЭДР И ПАРАЛЛЕЛЕПИПЕД

2. ТЕТРАЭДР

3. Одна из глав нашего курса будет посвящена многогранникам - поверхностям геометрических тел, составленным из многоугольников.

4. ВСПОМНИМ !!!

Какую фигуру в планиметрии мы
называли многоугольником?

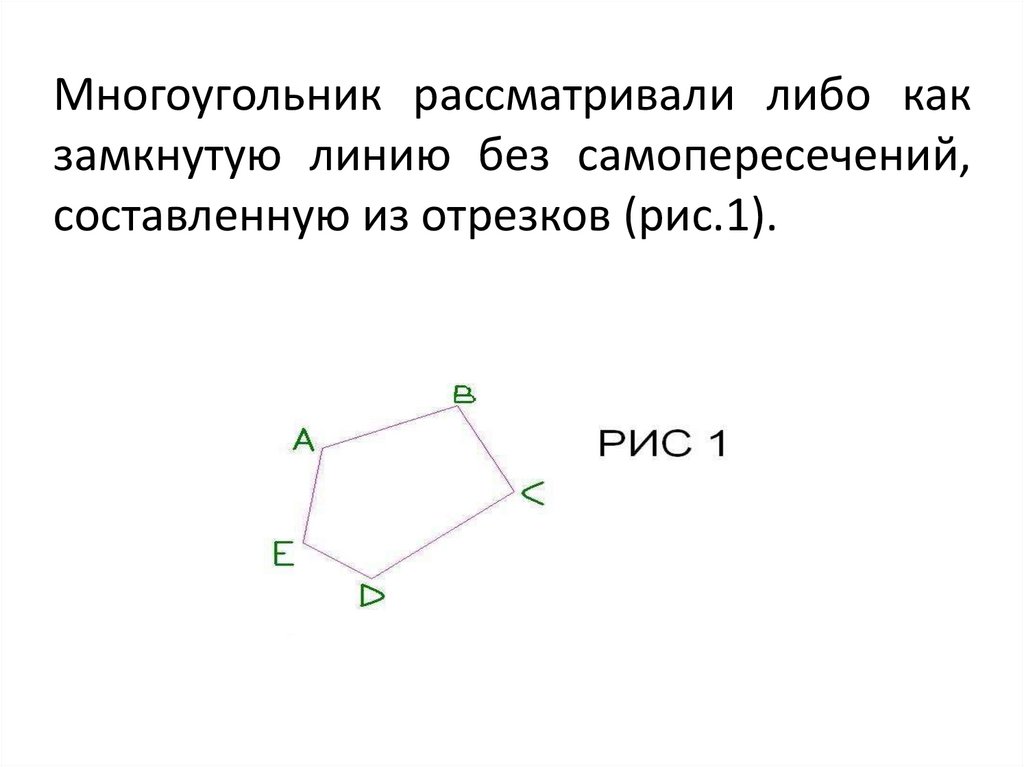
5. Многоугольник рассматривали либо как замкнутую линию без самопересечений, составленную из отрезков (рис.1).

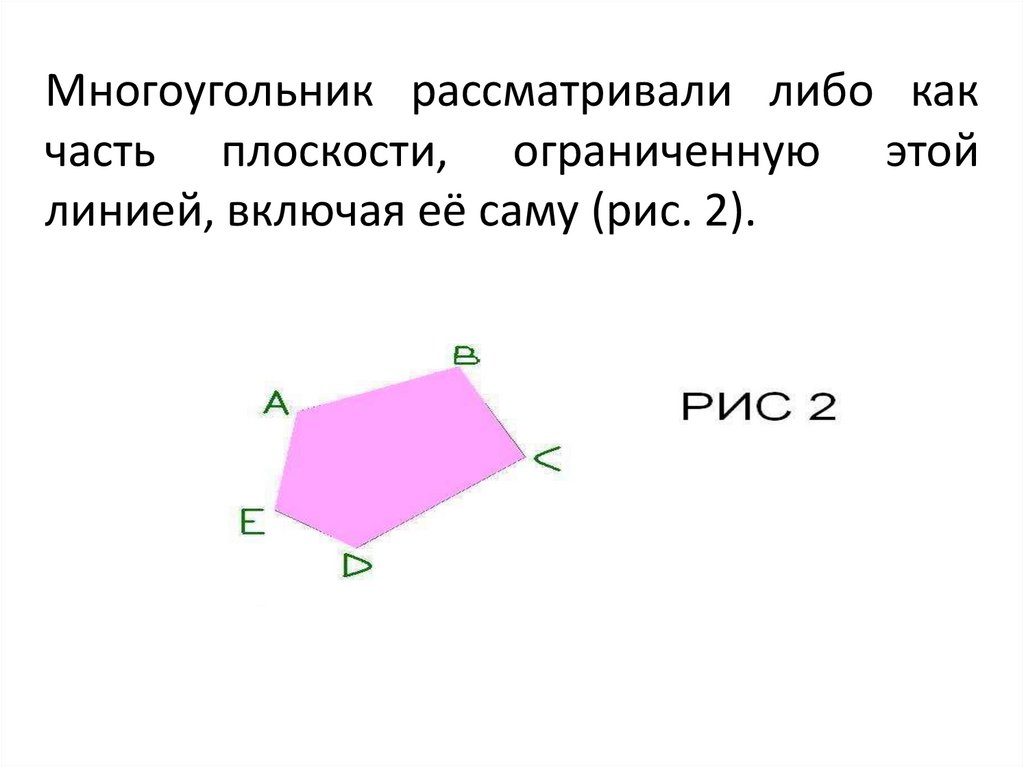
6. Многоугольник рассматривали либо как часть плоскости, ограниченную этой линией, включая её саму (рис. 2).

7.

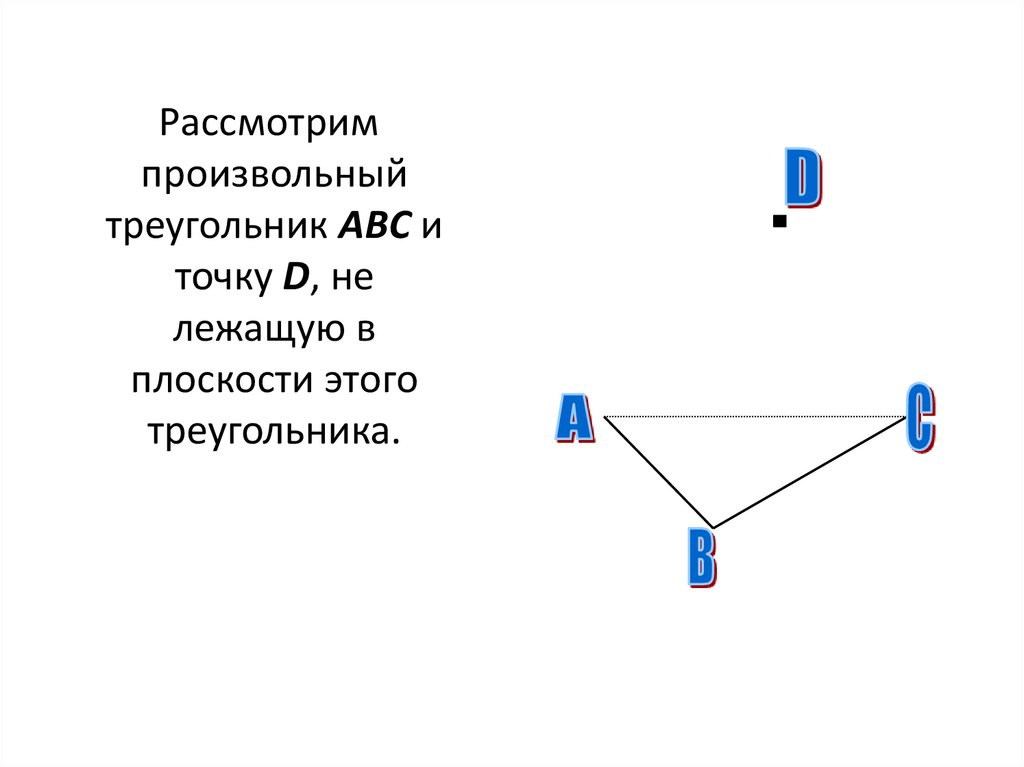
Рассмотрим
произвольный
треугольник АВС и
точку D, не
лежащую в
плоскости этого
треугольника.

8.

Соединив точку D отрезками с вершинами
треугольника АВС, получим треугольники DАВ,
DВС и DСА.

9.

Определение: поверхность, составленная из
четырёх треугольников АВС, DAB, DBC и DCA,
называется тетраэдром.
Обозначение: DАBC.
!!!! Первая буква в обозначении эта вершина, которая не
лежит в основании.

10.

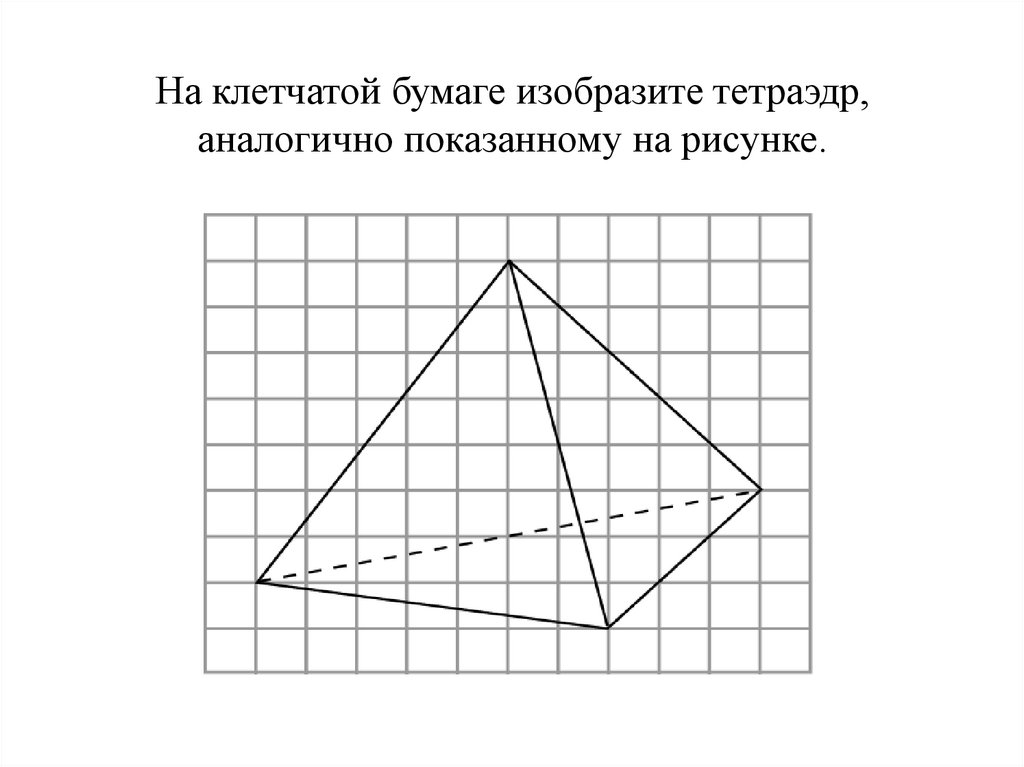
На клетчатой бумаге изобразите тетраэдр,
аналогично показанному на рисунке.

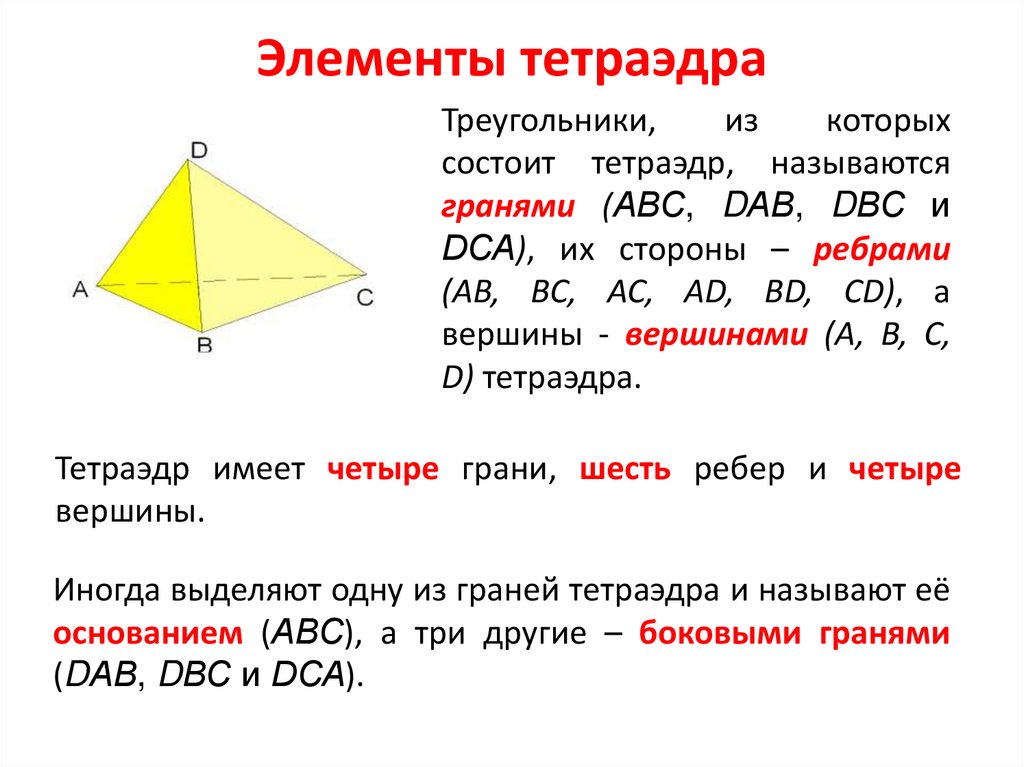
11. Элементы тетраэдра

Треугольники,
из
которых
состоит тетраэдр, называются
гранями (АВС, DАВ, DВС и
DСА), их стороны – ребрами
(AB, BC, AC, AD, BD, CD), а
вершины - вершинами (A, B, C,
D) тетраэдра.
Тетраэдр имеет четыре грани, шесть ребер и четыре
вершины.
Иногда выделяют одну из граней тетраэдра и называют её
основанием (АВС), а три другие – боковыми гранями
(DАВ, DВС и DСА).

12.

Примером применения в
архитектуре тетраэдра может
служить Великая пирамида в Гизе.
Она имеет форму правильного
тетраэдра и является древнейшим
из Семи чудес света.

13.

Разработанное для Нового
Орлеана «здание-город» NOAH
(New Orleans Arcology Habitat)
возвышается на 365 метров. В
тетраэдре помещаются
коммерческие организации,
три отеля, культурные
объекты, школа, больницы и
казино.

14. Тетраэдры в ювелирной промышленности

15. ПАРАЛЛЕЛЕПИПЕД

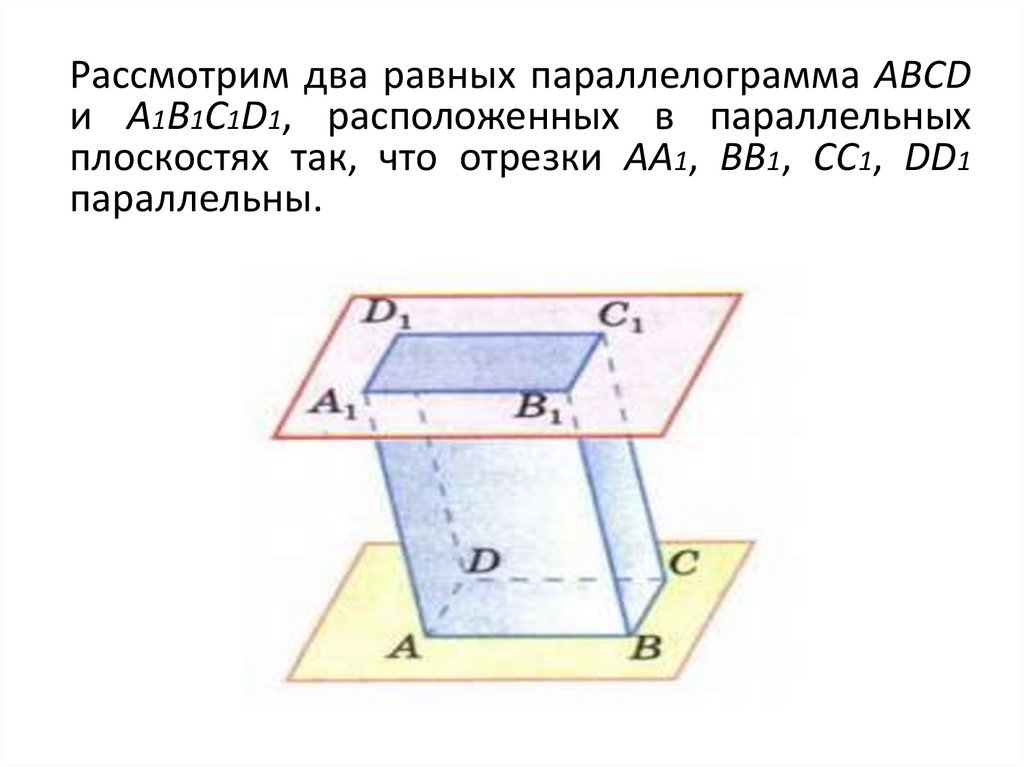
16.

Рассмотрим два равных параллелограмма ABCD
и A1B1C1D1, расположенных в параллельных
плоскостях так, что отрезки AA1, BB1, CC1, DD1
параллельны.

17.

Четырёхугольники
ABB1A1, BCC1B1, CDD1C1, DAA1D1 (1)
параллелограммы, т. к. каждый из них имеет
попарно параллельные противоположные
стороны.

18.

Определение: поверхность, составленная из двух
равных параллелограммов ABCD и A1B1C1D1 и четырёх
параллелограммов ABB1A1, BCC1B1, CDD1C1, DAA1D1
называется параллелепипедом.
Обозначается: ABCDA1B1C1D1.

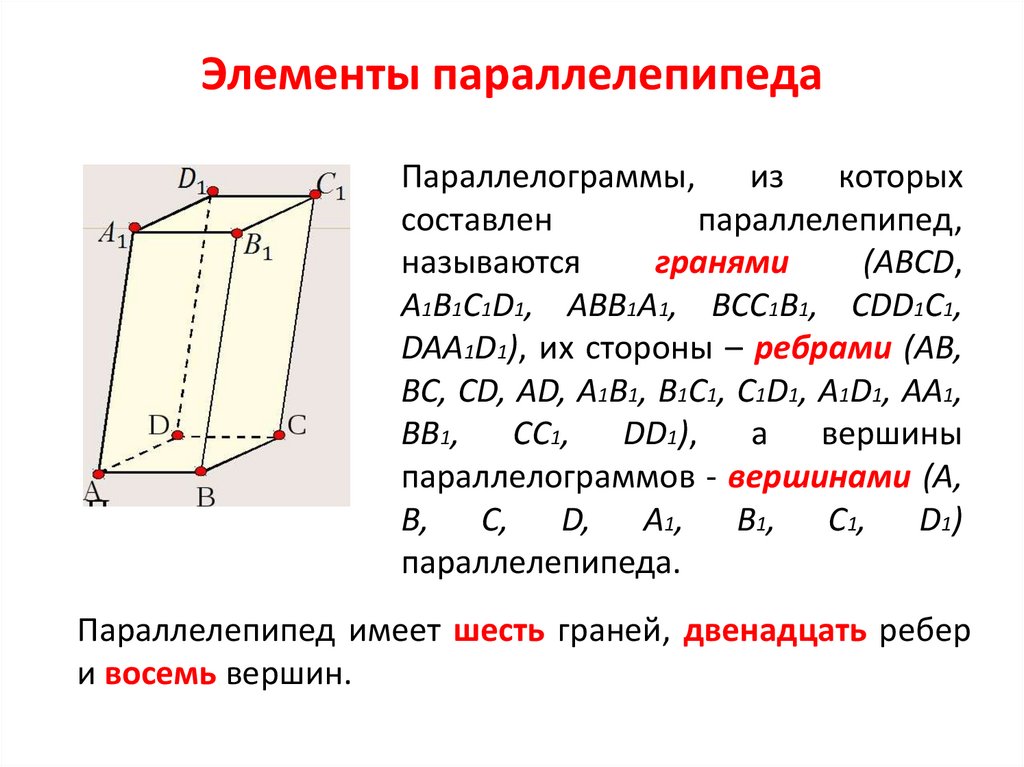
19. Элементы параллелепипеда

Параллелограммы,
из
которых
составлен
параллелепипед,
называются
гранями
(ABCD,
A1B1C1D1, ABB1A1, BCC1B1, CDD1C1,
DAA1D1), их стороны – ребрами (AB,
BC, CD, AD, A1B1, B1C1, C1D1, A1D1, AA1,
BB1, CC1, DD1), а вершины
параллелограммов - вершинами (A,
B, C, D, A1, B1, C1, D1)
параллелепипеда.
Параллелепипед имеет шесть граней, двенадцать ребер
и восемь вершин.

20.

Примеры использования формы
параллелепипеда

21.

22. ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД

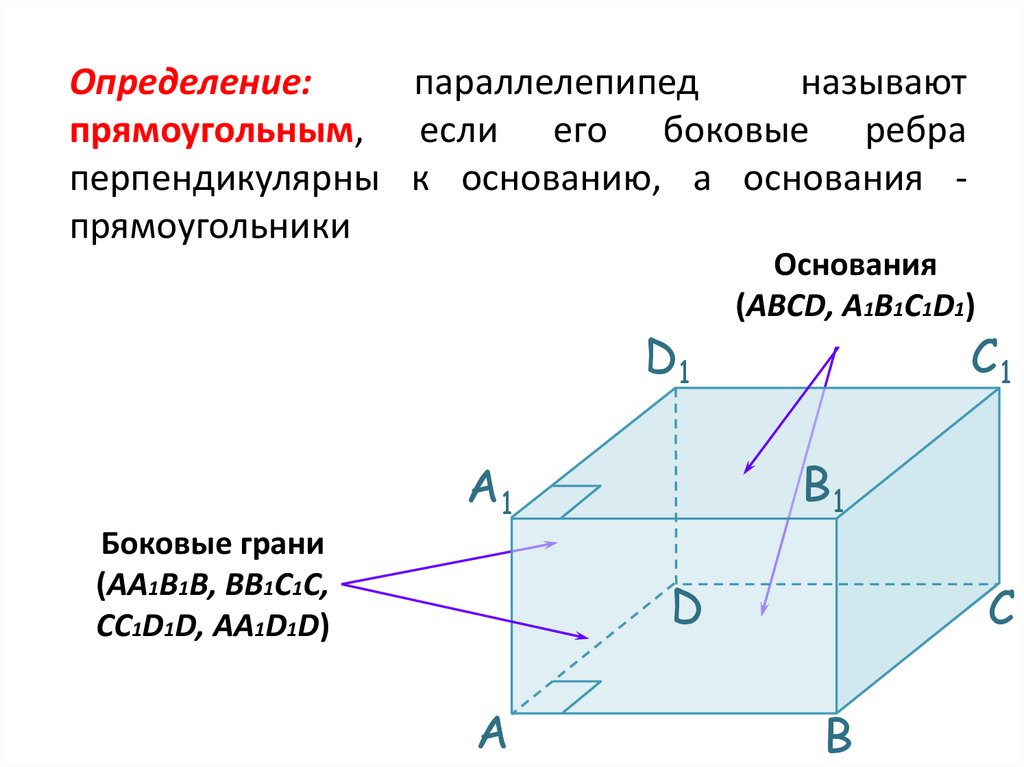
23.

Определение:
параллелепипед
называют
прямоугольным, если его боковые ребра
перпендикулярны к основанию, а основания прямоугольники
D1
C1
B1
А1
Боковые грани
(AA1B1B, BB1C1C,
CC1D1D, AA1D1D)
Основания
(ABCD, A1B1C1D1)
D
А
C
B

24.

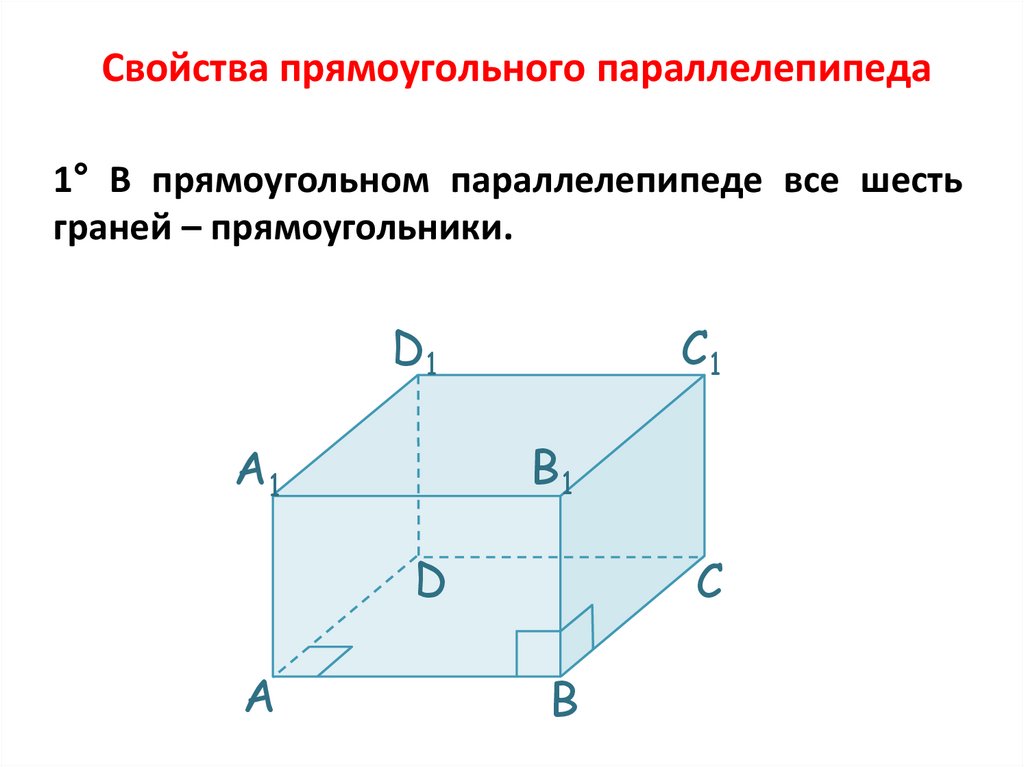
Свойства прямоугольного параллелепипеда
1° В прямоугольном параллелепипеде все шесть
граней – прямоугольники.
D1
C1
B1
А1
D
А
C
B

25.

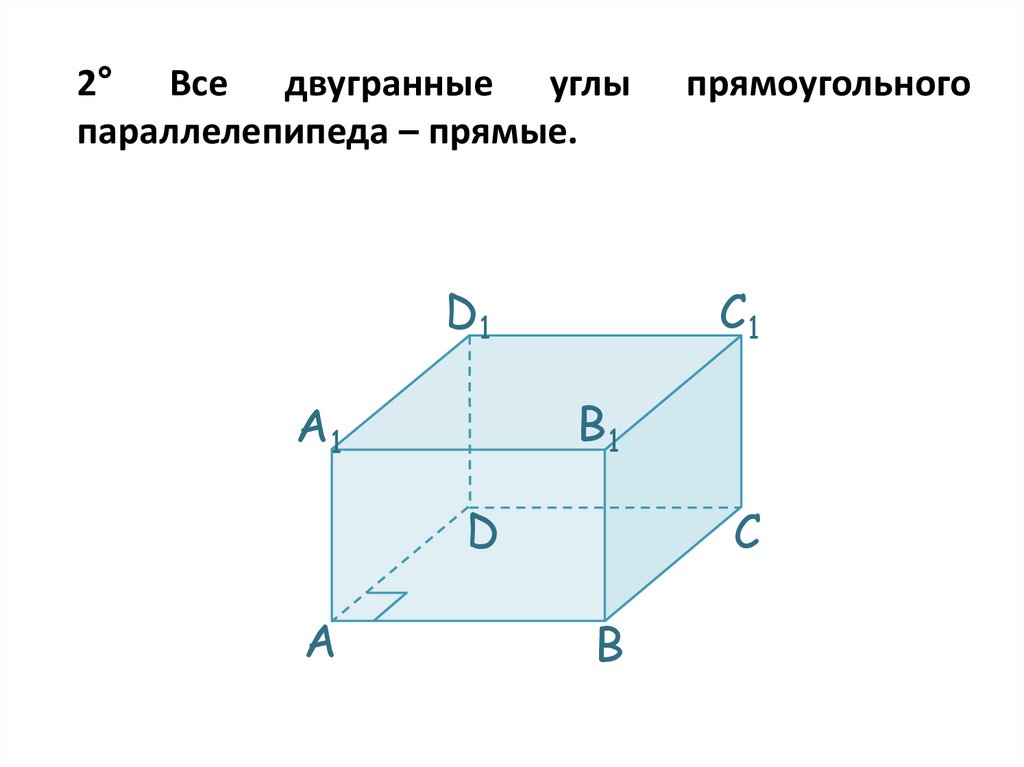
2° Все двугранные углы
параллелепипеда – прямые.
D1
C1
B1
А1
D
А
прямоугольного
C
B

26.

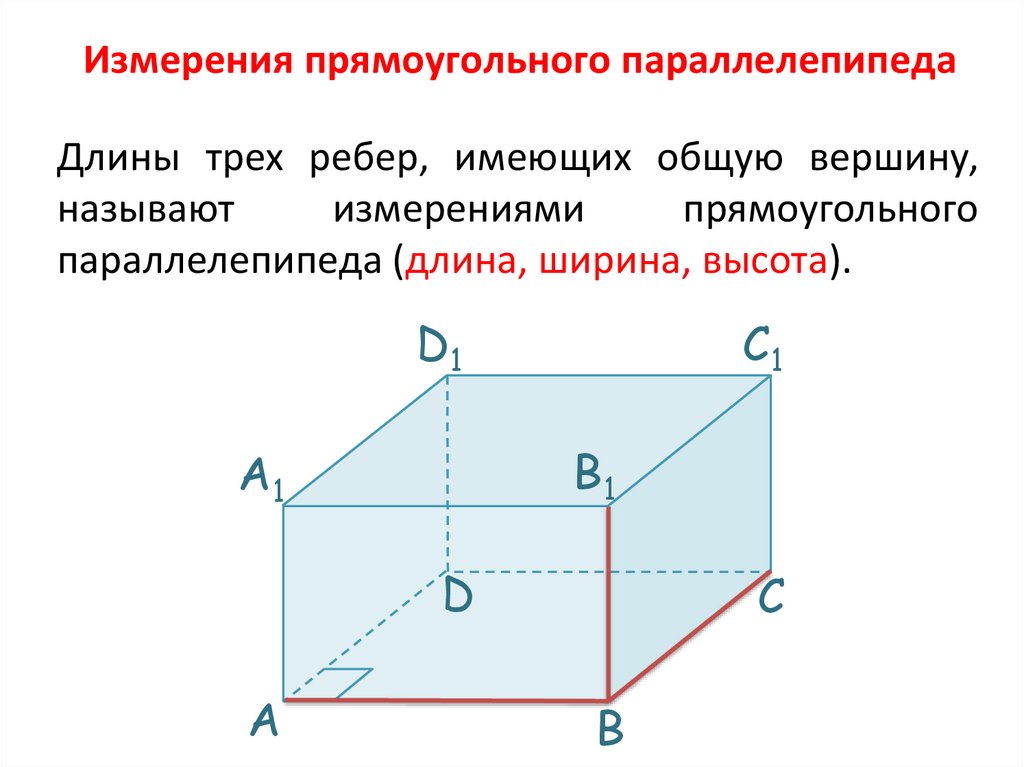
Измерения прямоугольного параллелепипеда
Длины трех ребер, имеющих общую вершину,
называют
измерениями
прямоугольного
параллелепипеда (длина, ширина, высота).
D1
C1
B1
А1
D
А
C
B

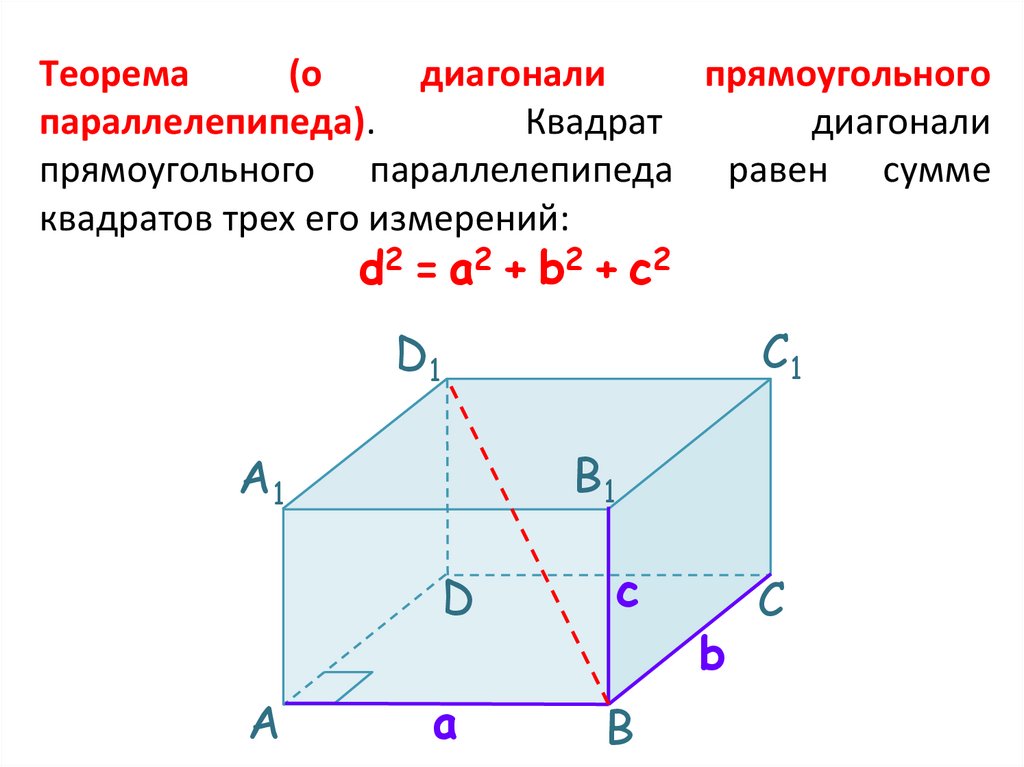
27.

Теорема
(о
диагонали
прямоугольного
параллелепипеда).
Квадрат
диагонали
прямоугольного параллелепипеда равен сумме
квадратов трех его измерений:
d2 = a2 + b2 + c2
C1
D1
B1
А1
А
D
c
a
B
b
C

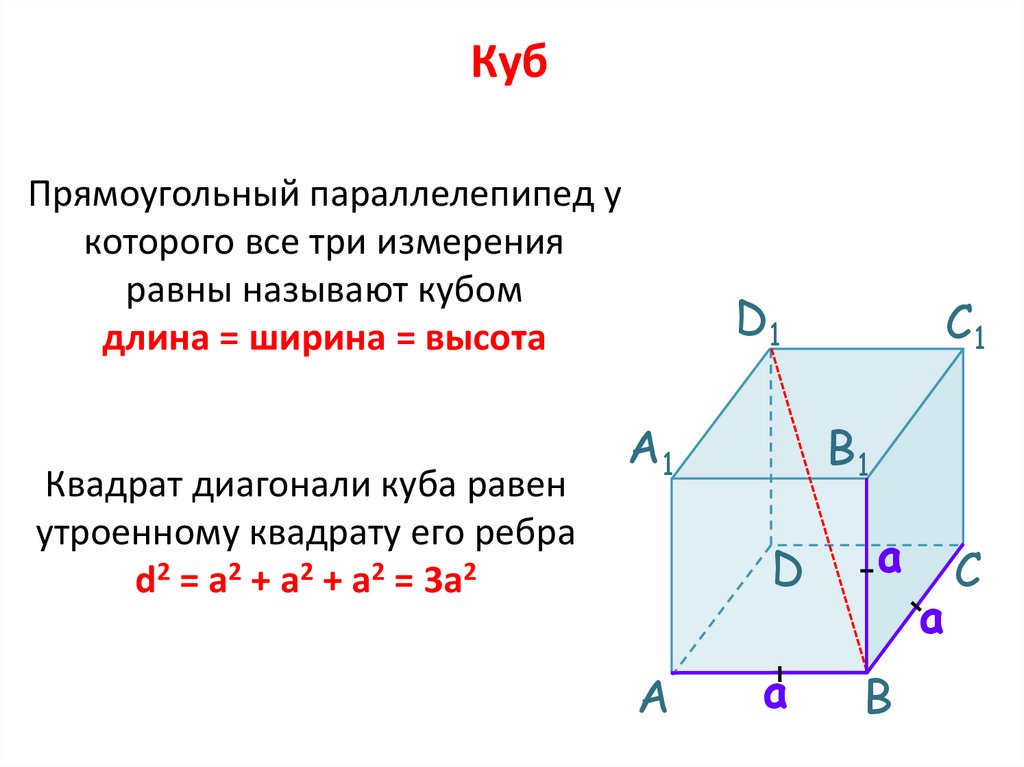
28.

Куб
Прямоугольный параллелепипед у
которого все три измерения
равны называют кубом
длина = ширина = высота
Квадрат диагонали куба равен
утроенному квадрату его ребра
d2 = a2 + а2 + а2 = 3a2
D1
А1
А
C1
B1
D
a
a
B
a
C

29. СПАСИБО ЗА ВНИМАНИЕ!