Параллелепипед. Определение

1.

Параллелепипед

2.

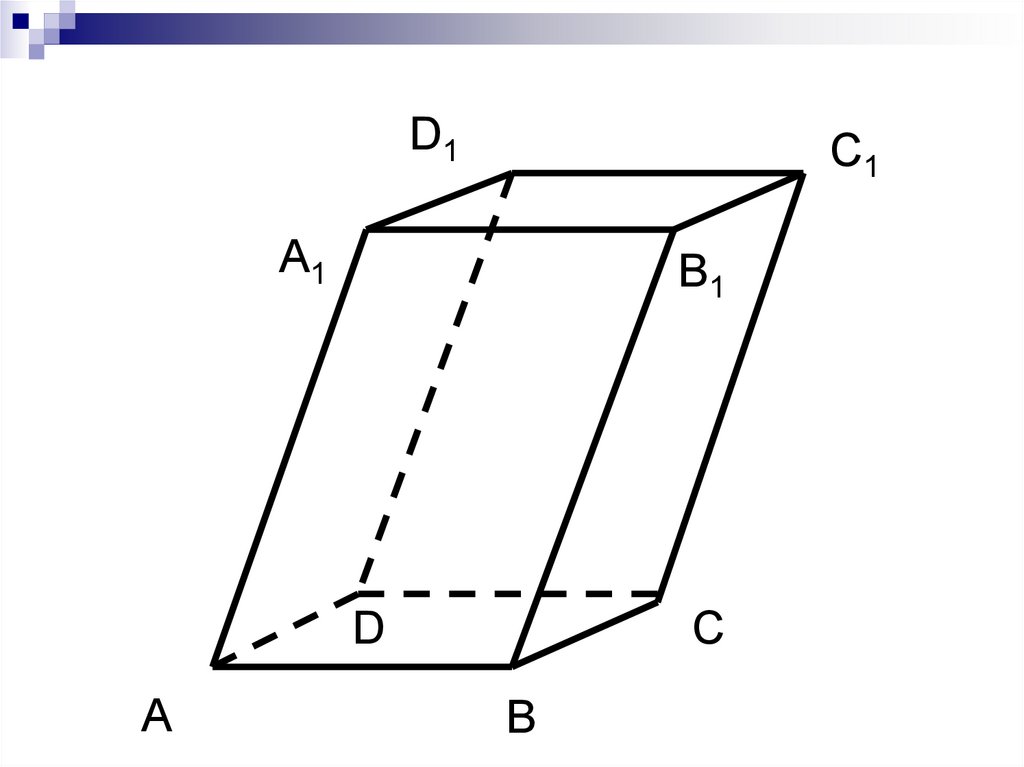
D1
C1
А1
B1
С
D
А
В

3.

ОПРЕДЕЛЕНИЕ:
D1
C1
А1
B1
С
D
А
В
Геометрическое тело или
многогранник, состоящий из трёх пар
равных параллелограммов лежащих в
параллельных плоскостях, называется
параллелепипедом

4. Смежные грани

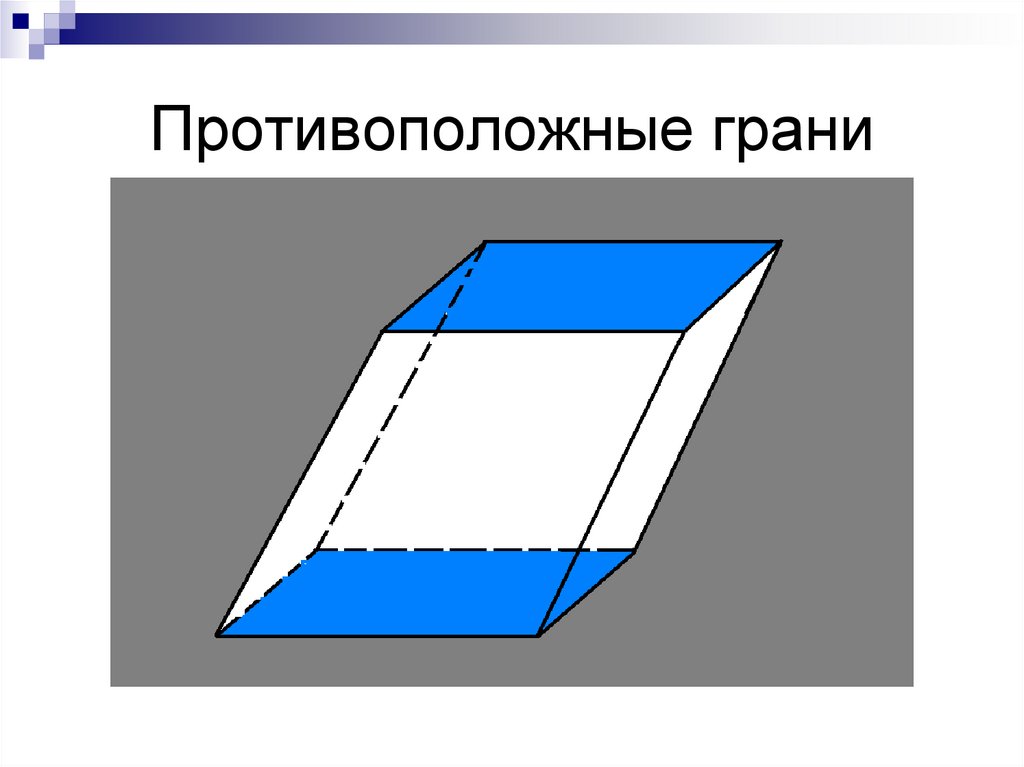
5. Противоположные грани

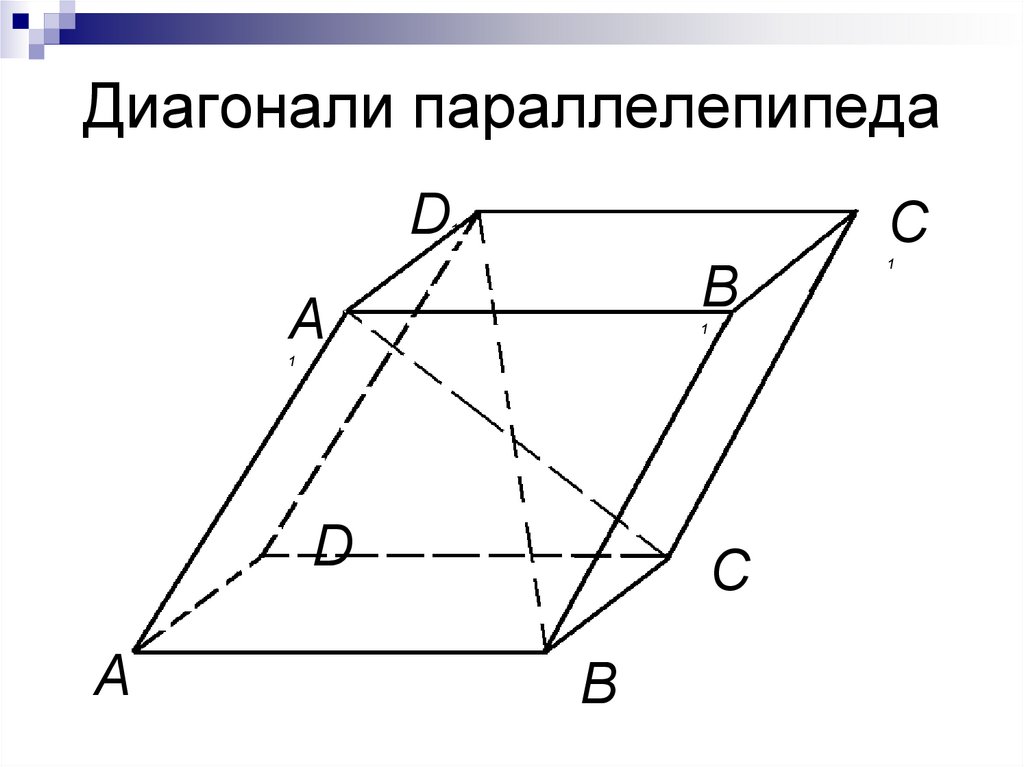
6. Диагонали параллелепипеда

D
C
1
B
A
1
1
D
A
C
B
1

7. Свойства параллелепипеда

8.

1. У параллелепипеда все шесть гранейпараллелограммы
2. У ПРЯМОГО параллелепипеда четыре боковые
грани- прямоугольники, а два основанияпараллелограммы
3. У ПРЯМОГО ПРЯМОУГОЛЬНОГО
ПАРАЛЛЕЛЕПИПЕДА все шесть гранейпрямоугольники.
4. Диагонали прямоугольного параллелепипеда
равны.

9.

Три ребра
прямоугольного
параллелепипеда,
сходящиеся к одной
вершине, называются
его измерениями; одно
из них можно
рассматривать как
длину, другое- как
ширину, а третье- как
высоту.
Прямоугольный
параллелепипед,
имеющий равные
измерения, называется
кубом. У куба все грани
квадраты.

10. Свойства граней и диагоналей параллелепипеда:

1. Противоположный грани равны и
параллельны.
2. Все четыре диагонали пересекаются
в одной точке и делятся в ней пополам.

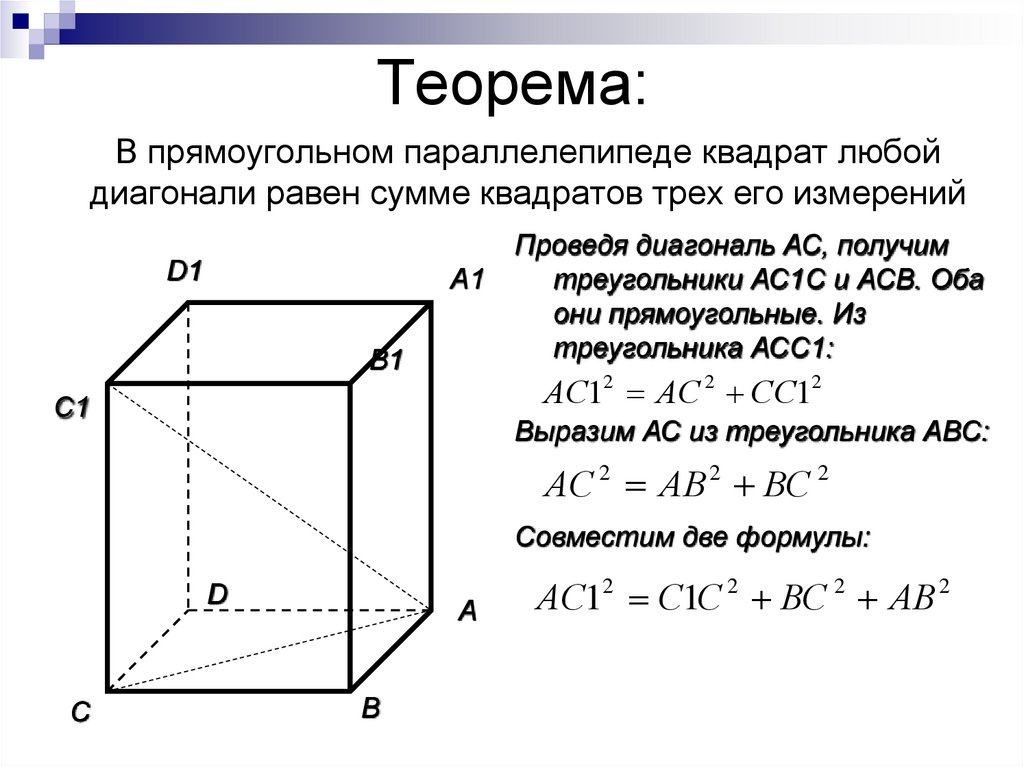
11. Теорема:

В прямоугольном параллелепипеде квадрат любой
диагонали равен сумме квадратов трех его измерений
D1
A1
B1
Проведя диагональ АС, получим
треугольники АС1С и АСВ. Оба
они прямоугольные. Из
треугольника АСС1:
АС12 АС 2 СС12
C1
Выразим АС из треугольника АВС:
АС 2 АВ 2 ВС 2
Совместим две формулы:
D
C
A
B
АС12 С1С 2 ВС 2 АВ 2

12.

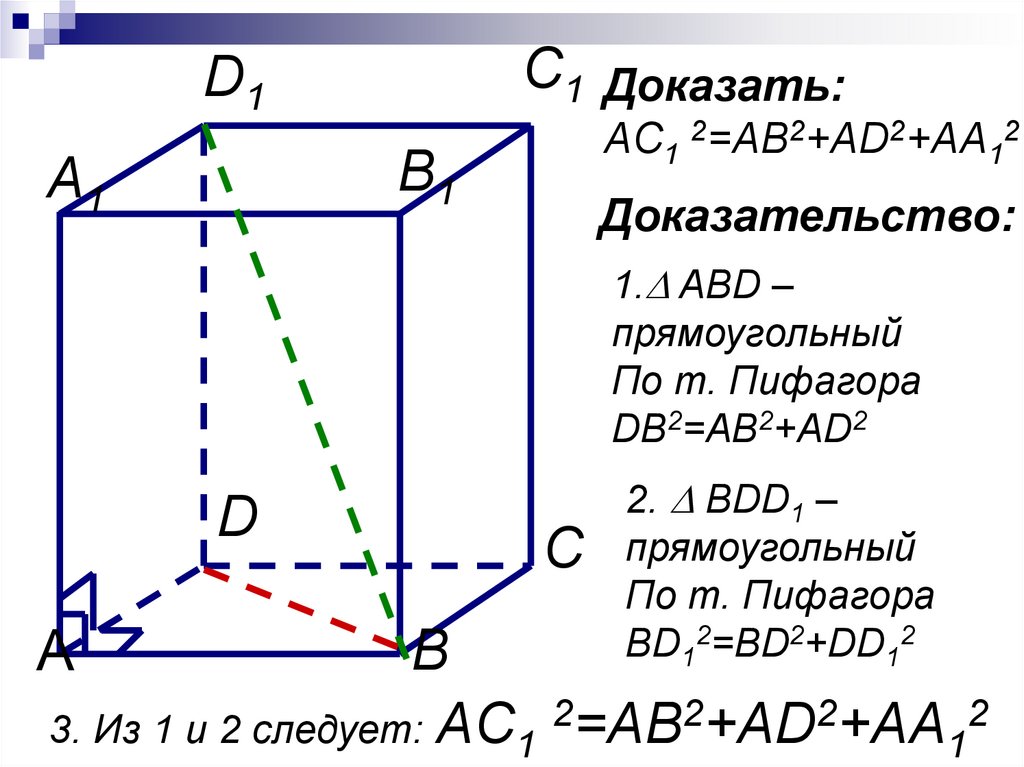
C1 Доказать:
D1
AC1 2=AB2+AD2+AA12
B1
A1
Доказательство:
1. ABD –
прямоугольный
По т. Пифагора
DB2=AB2+AD2
D
С
2. BDD1 –
прямоугольный
По т. Пифагора
BD12=BD2+DD12
В
3. Из 1 и 2 следует: AC1 2=AB2+AD2+AA12
А

13.

ВИДЫ ПАРАЛЛЕЛЕПИПЕДА

14.

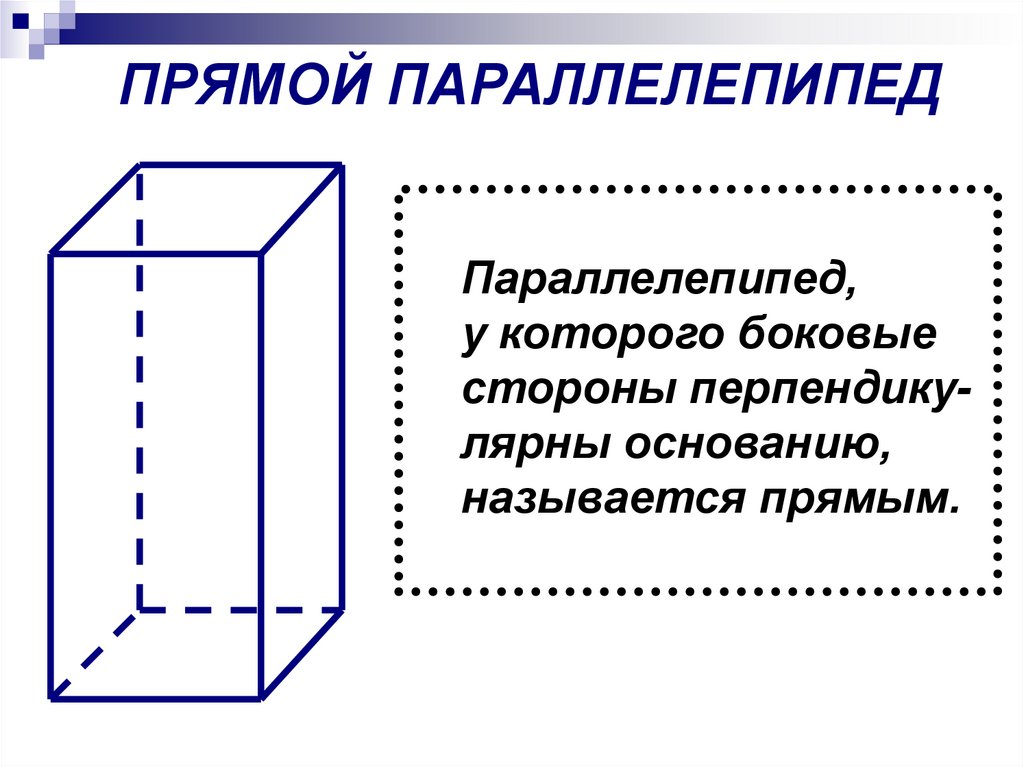
ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕД
Параллелепипед,
у которого боковые
стороны перпендикулярны основанию,
называется прямым.

15.

ПРЯМОУГОЛЬНЫЙ
ПАРАЛЛЕЛЕПИПЕД
Параллелепипед называется прямоугольным, если его боковые рёбра перпендикулярны к основанию, а основания являются прямоугольниками.

16.

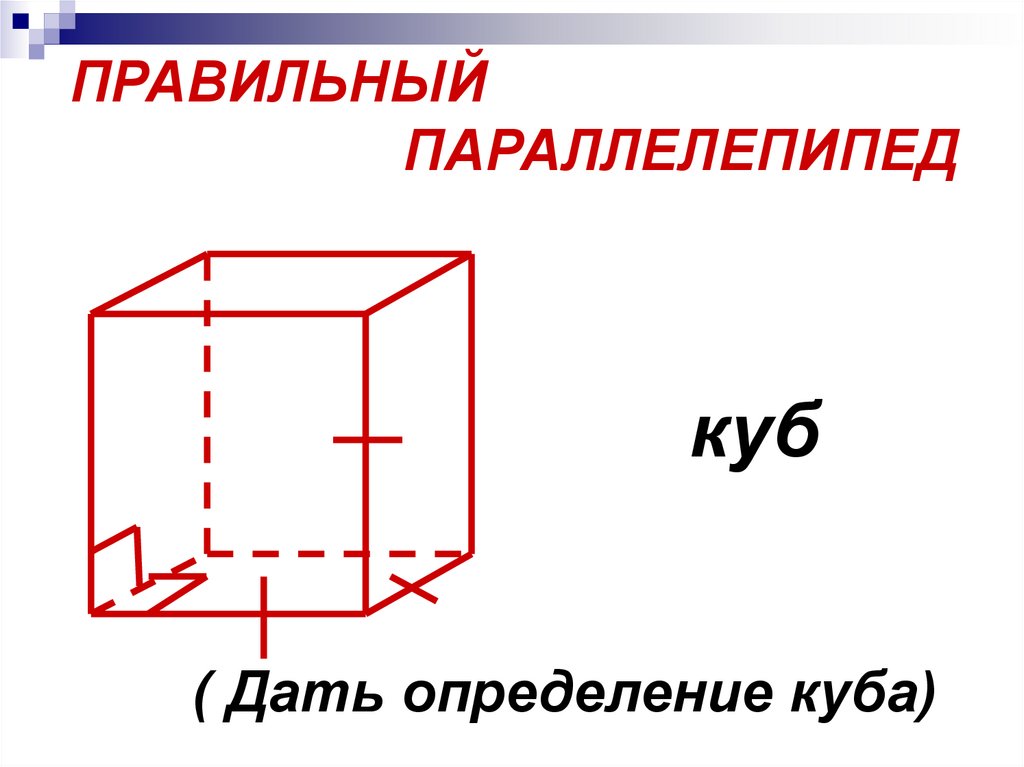
ПРАВИЛЬНЫЙ
ПАРАЛЛЕЛЕПИПЕД
куб
( Дать определение куба)

17.

C1
D1
B1
A1
D
А
С
В
1. В прямоугольном параллелепипеде
все шесть граней – прямоугольники.
2. Все двугранные углы прямоугольного параллелепипеда – прямые.

18. Параллелепипед, все грани которого – ромбы, называется РОМБОЭДР. Форму ромбоэдра имеют кристаллы исландского шпата