Призма. Определение, элементы, виды

1. призма

Определение,
элементы, виды.
«Геометрия» Л. С. Атанасян
стр. 60 §1 п.25,27;
стр.24 §4 п.13.

2. План :

П
Р
И
З
М
А
План :
Определение призмы (п.27 стр.62)
Элементы призмы
(п.27 стр.63)
Виды призмы
(п.27 стр.63)
Площади боковой и полной
поверхностей, объём призмы
(п.27 стр.63)

3. Тест на концентрацию внимания

П
Р
И
З
М
А
Тест на концентрацию внимания
В течении одной минуты найдите соответствие между названием
формулы и ее математическим выражением.
1.
2.
3.
4.
5.
6.
7.
8.
9.
Площадь равностороннего
треугольника
Формула Герона
Площадь ромба
Теорема Пифагора
Площадь прямоугольного
треугольника
Теорема косинусов
Сторона равностороннего
треугольника через радиус
описанной окружности
Радиус описанной около
квадрата окружности
Площадь трапеции
А)
А)
Б)
Б
В))
В
Г))
Г)
Д)
Д)
Е)
Е)
Ж)
Ж)
З))
З
И ))
И
2
S ap
( p3 a )( p b)( p c )
S
c 2 a 2 4 b 2
S
p c 2a )(bc
p
b)(
p c)
a 2 bp2(
cos
12 3
a
S
S 2 d1 d 2
4
2
2
2
c aa
b
2
R 1
2
S ch
c
2 3
a R
a 2 b 2 c 2 bc cos
1
S d1 d 2
a R
2 3
1
a 2
S
R 2 chc
2
a
b
b
a
S
h
S
h
2
2

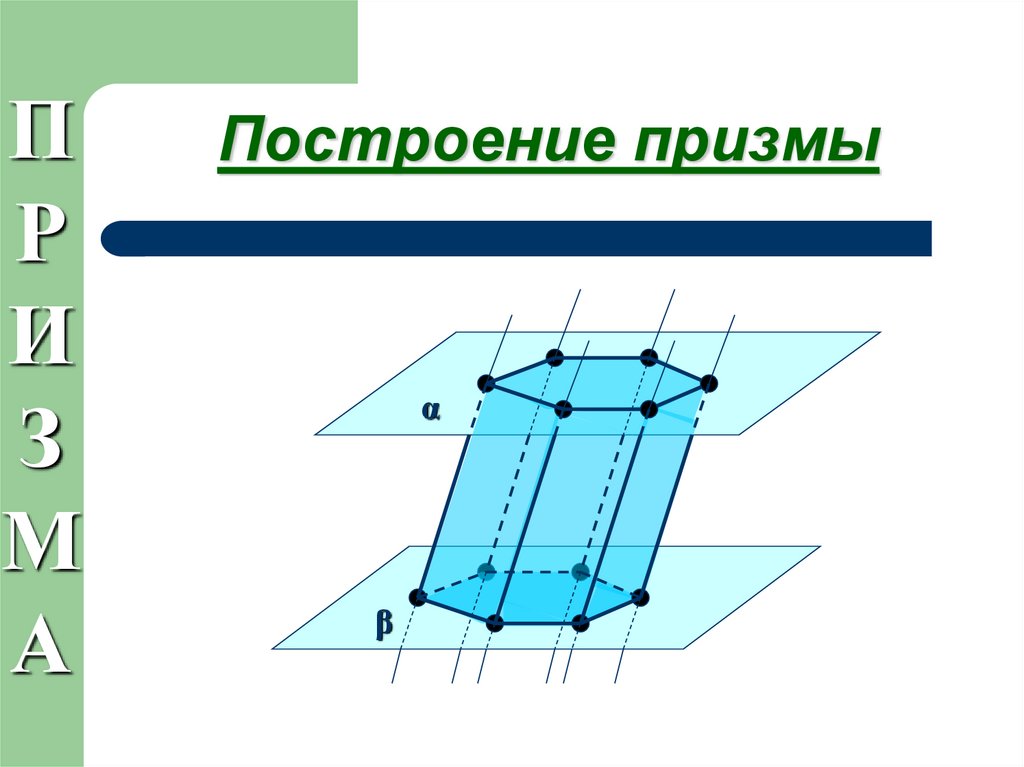
4. Построение призмы

П
Р
И
З
М
А
Построение призмы
α
β

5.

П
Р
И
З
М
А
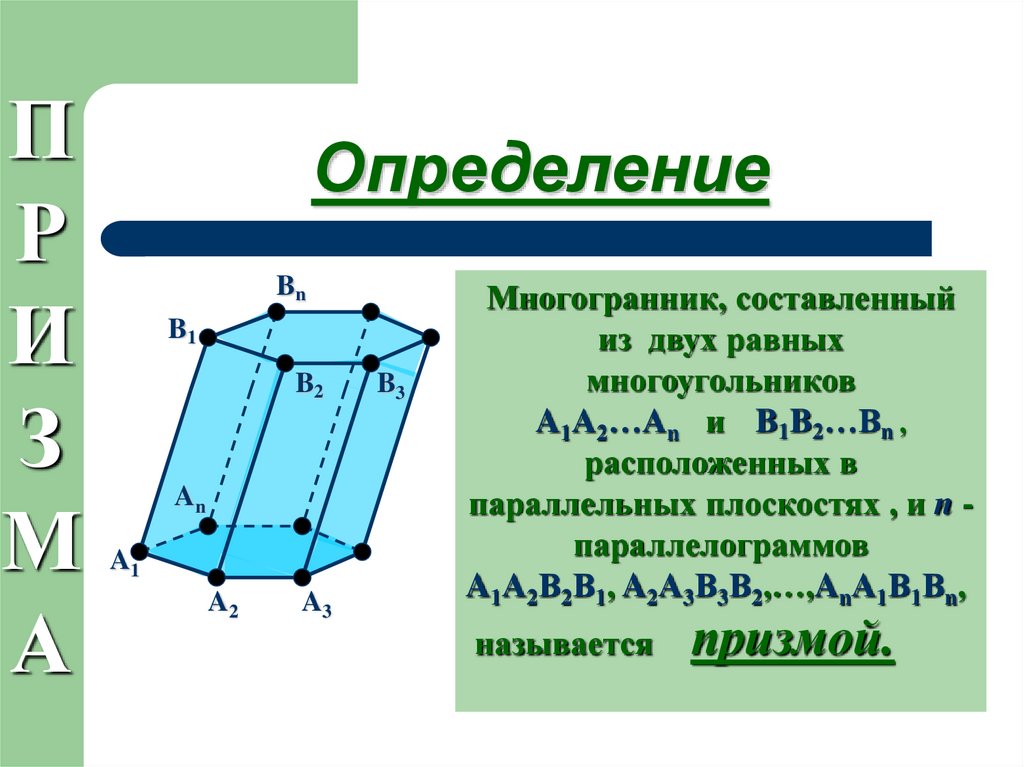
Определение
Bn
B1
B2
An
A1
A2
A3
B3
Многогранник, составленный
из двух равных
многоугольников
A1А2…Аn и B1B2…Bn ,
расположенных в
параллельных плоскостях , и n параллелограммов
A1А2В2В1, A2А3В3В2,…,AnА1В1Вn,
называется
призмой.

6.

П
Р
И
З
МТермин «призма» греческого происхождения
А и буквально означает «отпиленное» тело.

7.

П
Р
И
З
М
А
В XI книге «Начал» Евклид дает следующее определение призмы:
«Призма есть телесная(т.е. пространственная) фигура, заключенная между
плоскостями, из которых две противоположные равны и параллельны,
остальные же параллелограммы.

8. Элементы призмы.

П Элементы призмы.
Р
И
З
М
А
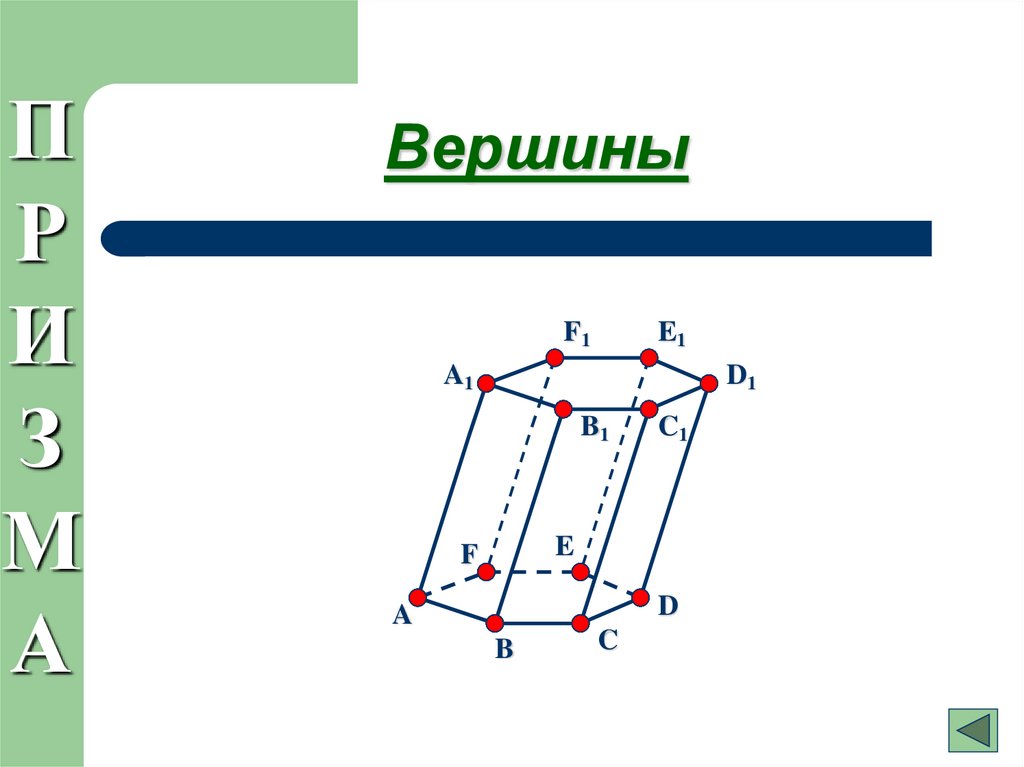
1. Вершины A,B,C,D,E,F,A1,B1,C1,D1,E1,F1
2.
Ребра
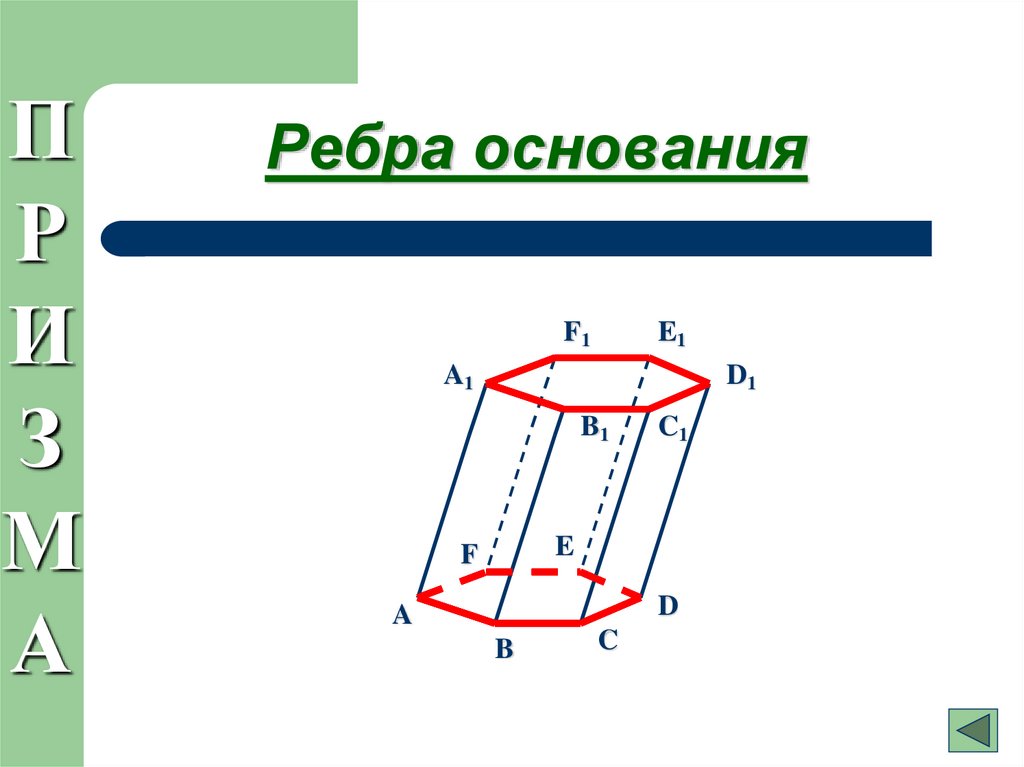
Основания: AB,BC,…,A1D1,B1C1,…
2n
3n
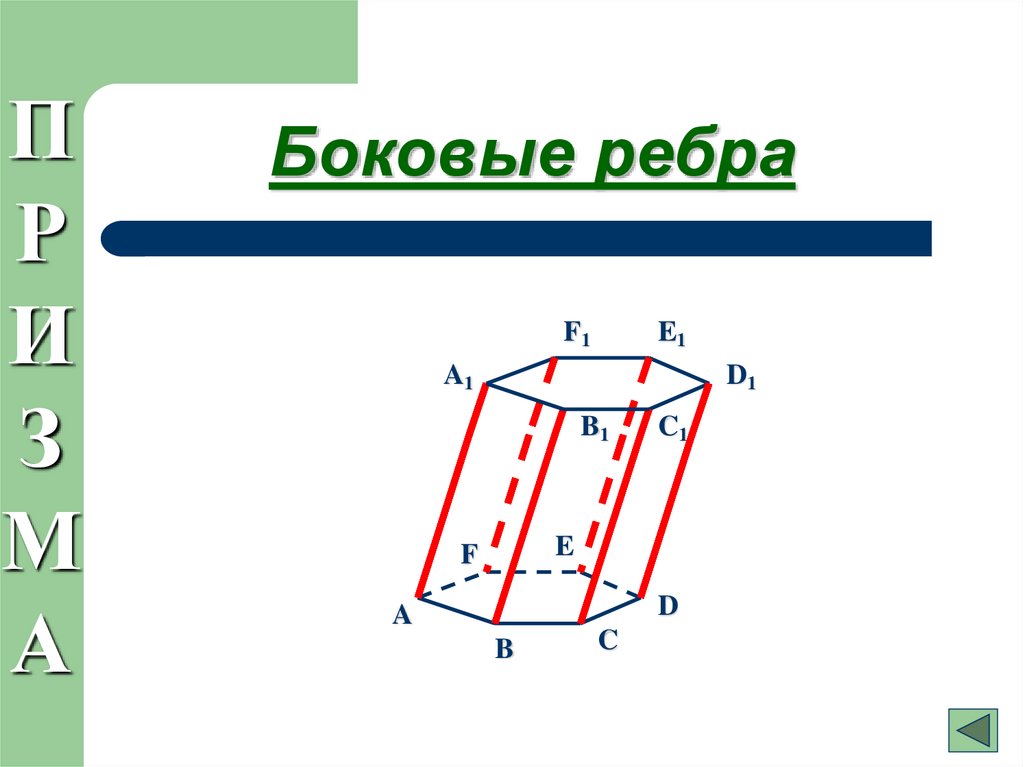
Боковые: AA1, DD1, BB1, CC1, EE1, FF1
3.
Грани
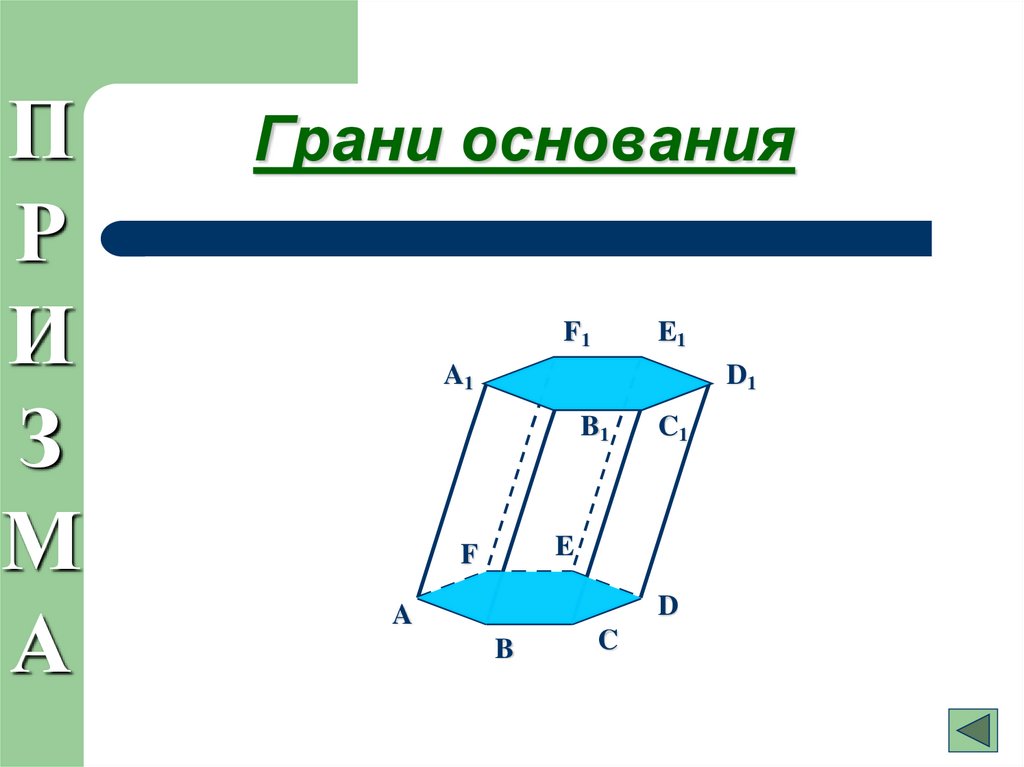
Основания: ABCDEF, A1B1C1D1E1F1
n+2
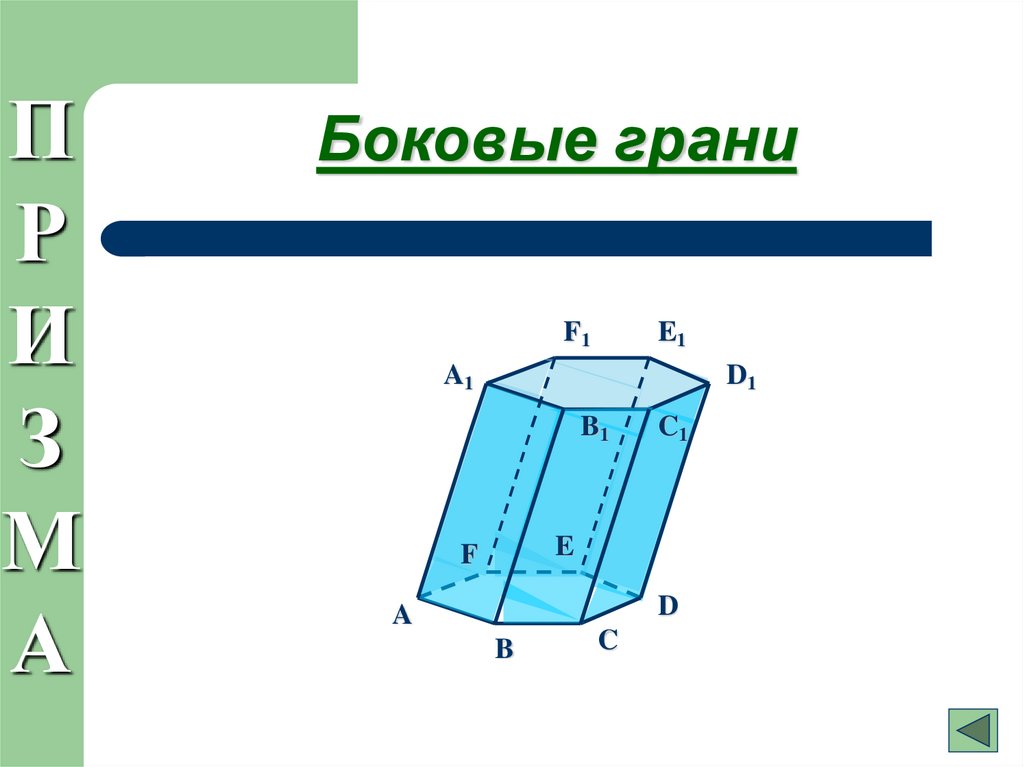
Боковые: AA1B1B, CC1D1D, …
4.
5.
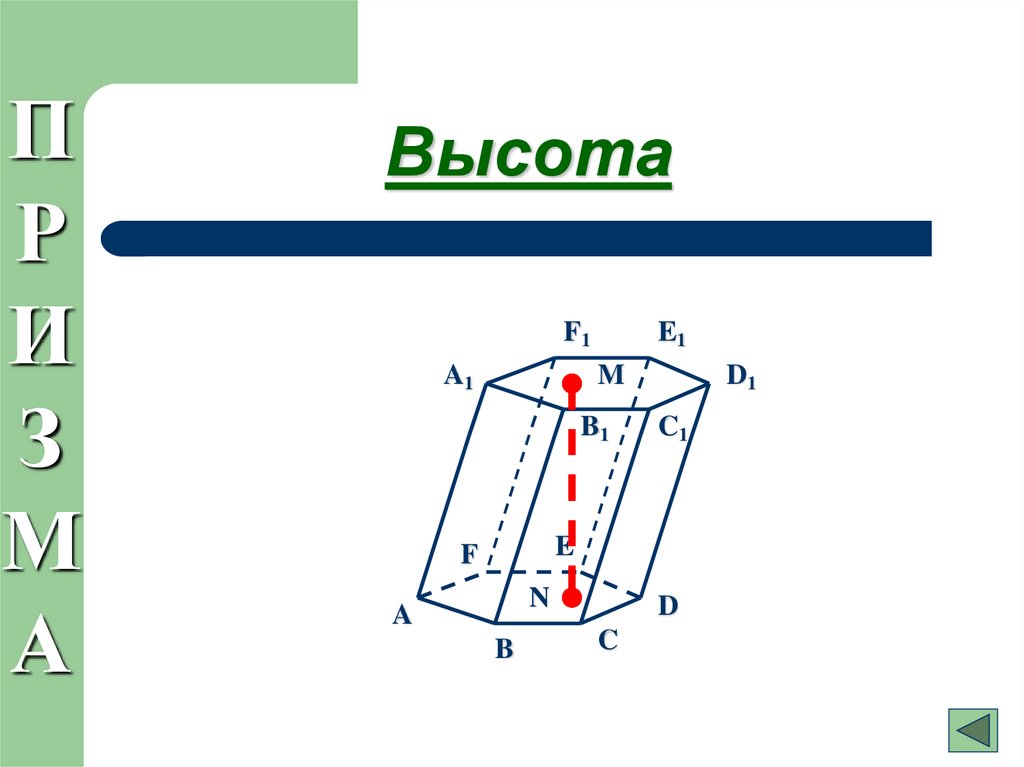
Высота
MN=H – высота призмы
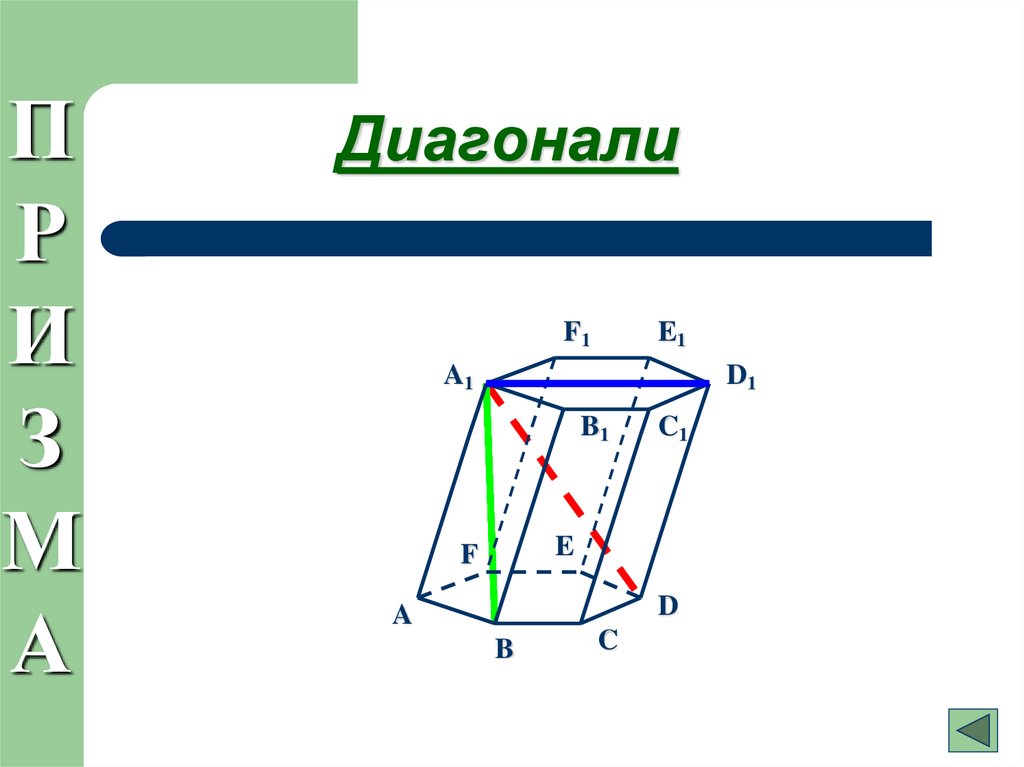
Диагональ Призмы: A1D, AD1, …
Боковой грани: A1B, B1C, C1D, …
Основания: AD, A1D1, …
n(n-3)

9. Вершины

П
Р
И
З
М
А
Вершины
F1
E1
A1
D1
B1
C1
E
F
D
A
B
C

10. Ребра основания

П
Р
И
З
М
А
Ребра основания
F1
E1
A1
D1
B1
C1
E
F
D
A
B
C

11. Боковые ребра

П
Р
И
З
М
А
Боковые ребра
F1
E1
A1
D1
B1
C1
E
F
D
A
B
C

12. Грани основания

П
Р
И
З
М
А
Грани основания
F1
E1
A1
D1
B1
C1
E
F
D
A
B
C

13. Боковые грани

П
Р
И
З
М
А
Боковые грани
F1
E1
A1
D1
B1
C1
E
F
D
A
B
C

14. Высота

П
Р
И
З
М
А
Высота
F1
A1
E1
M
B1
D1
C1
E
F
N
A
B
D
C

15. Диагонали

П
Р
И
З
М
А
Диагонали
F1
E1
A1
D1
B1
C1
E
F
D
A
B
C

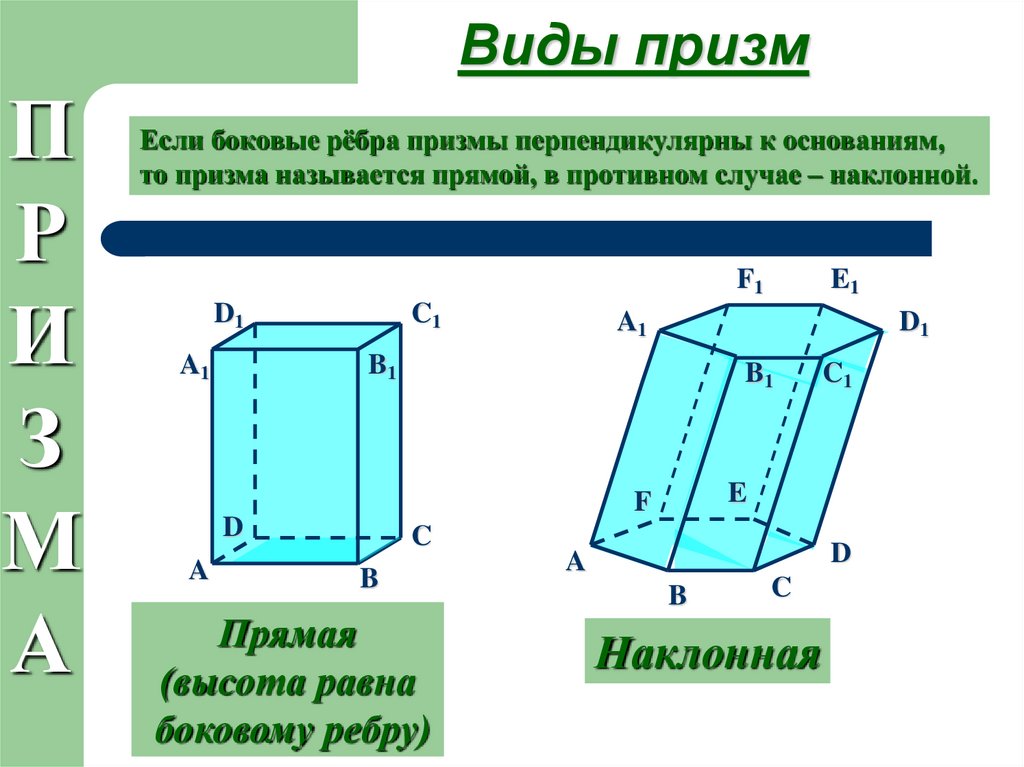
16. Виды призм

П
Р
И
З
М
А
Если боковые рёбра призмы перпендикулярны к основаниям,
то призма называется прямой, в противном случае – наклонной.
F1
D1
A1
C1
A
A1
D1
B1
B1
C
B
Прямая
(высота равна
боковому ребру)
C1
E
F
D
E1
D
A
B
C
Наклонная

17.

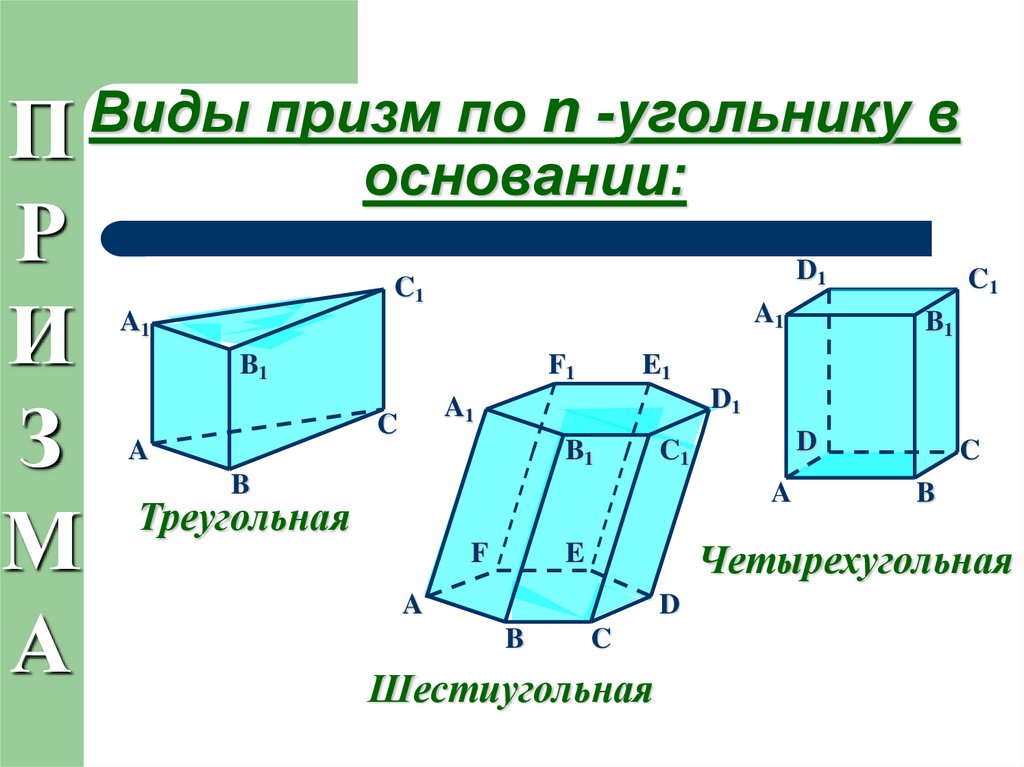
Виды
призм
по
n
-угольнику
в
П
основании:
Р
И
З
М
А
D1
C1
A1
A1
B1
F1
A
B1
E1
D1
A1
C
C1
B1
D
C1
B
A
Треугольная
F
B
Четырехугольная
E
A
D
B
C
C
Шестиугольная

18.

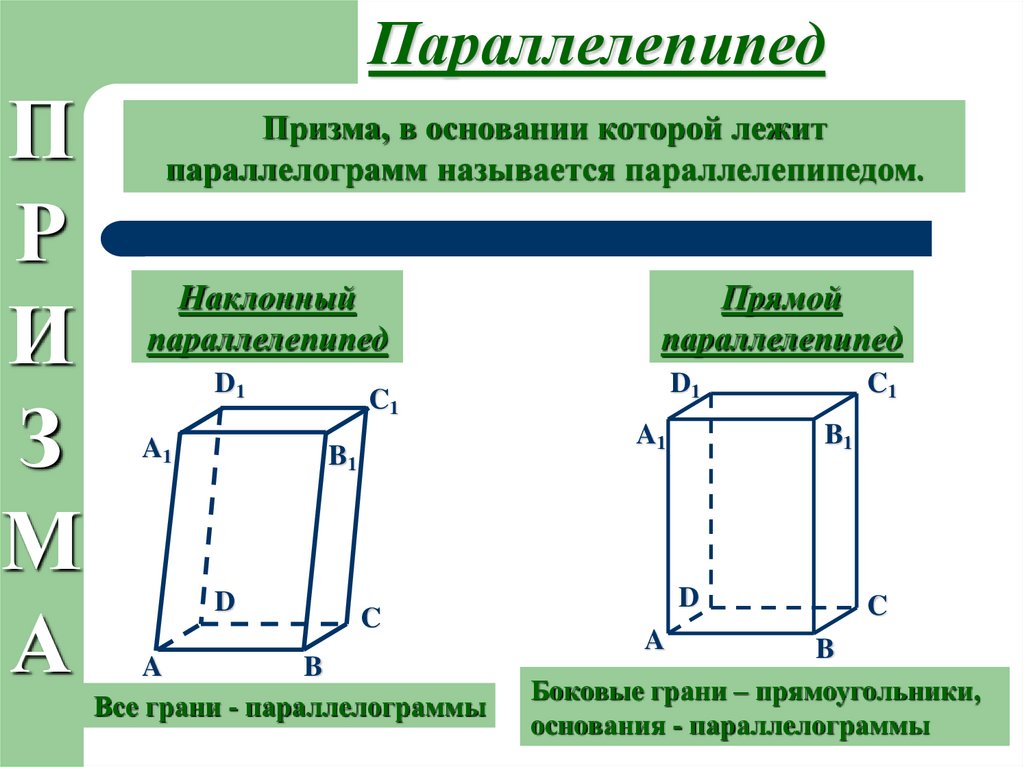
Параллелепипед
П
Р
И
З
М
А
Призма, в основании которой лежит
параллелограмм называется параллелепипедом.
Наклонный
параллелепипед
D1
A1
D1
C1
A1
B1
D
Прямой
параллелепипед
C
A
B
Все грани - параллелограммы
B1
D
A
C1
C
B
Боковые грани – прямоугольники,
основания - параллелограммы

19.

П
Р
И
З
М
А
Прямоугольный
параллелепипед
D1
A1
C1
B1
Куб
D1
A1
C1
B1
D
A
D
A
C
B
Прямая призма,
все грани которой
прямоугольники
C
B
Прямая призма, все
грани которой
квадраты.

20.

П
Р
И
З
М
А
Параллелепипед.
Свойства.
1. Противоположные грани параллелепипеда равны
и параллельны.
D1
C1
A1
B1
О
D
A
C
B
2. Любая грань параллелепипеда
может являться его
основанием.
3. Все четыре диагонали
параллелепипеда
пересекаются в одной точке и
делятся ею пополам.

21.

П
Р
И
З
М
А
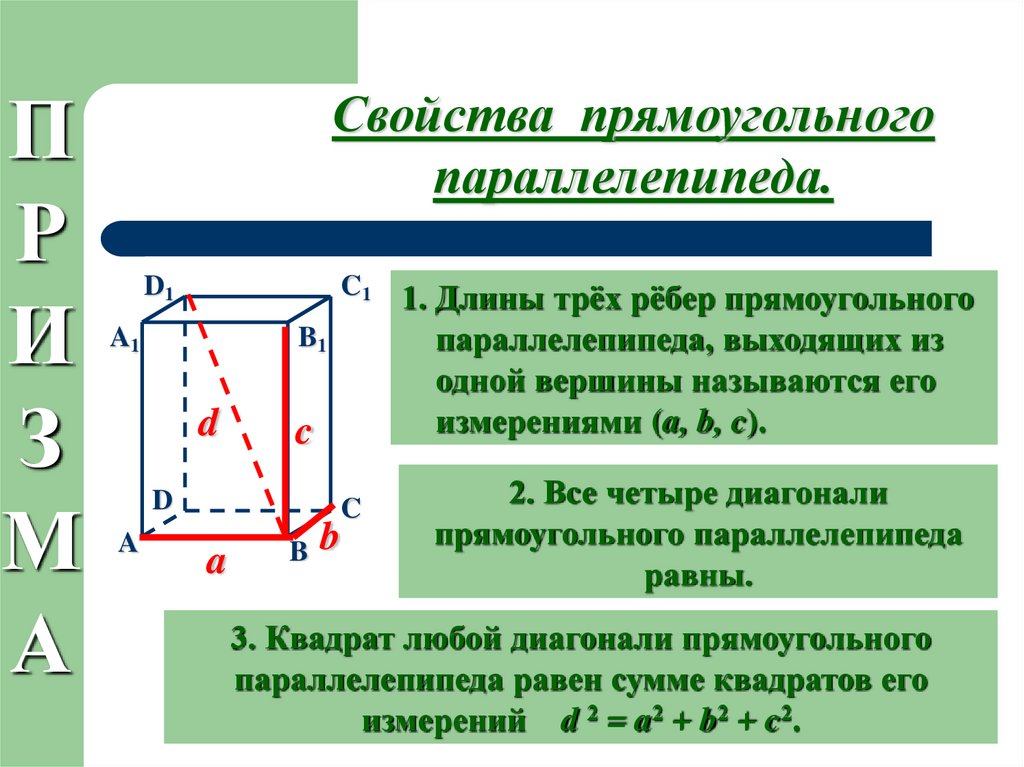
Свойства прямоугольного
параллелепипеда.
D1
C1
A1
B1
d
c
D
A
a
B
b
C
1. Длины трёх рёбер прямоугольного
параллелепипеда, выходящих из
одной вершины называются его
измерениями (a, b, c).
2. Все четыре диагонали
прямоугольного параллелепипеда
равны.
3. Квадрат любой диагонали прямоугольного
параллелепипеда равен сумме квадратов его
измерений d 2 = a2 + b2 + c2.

22.

П
Р
И
З
М
А
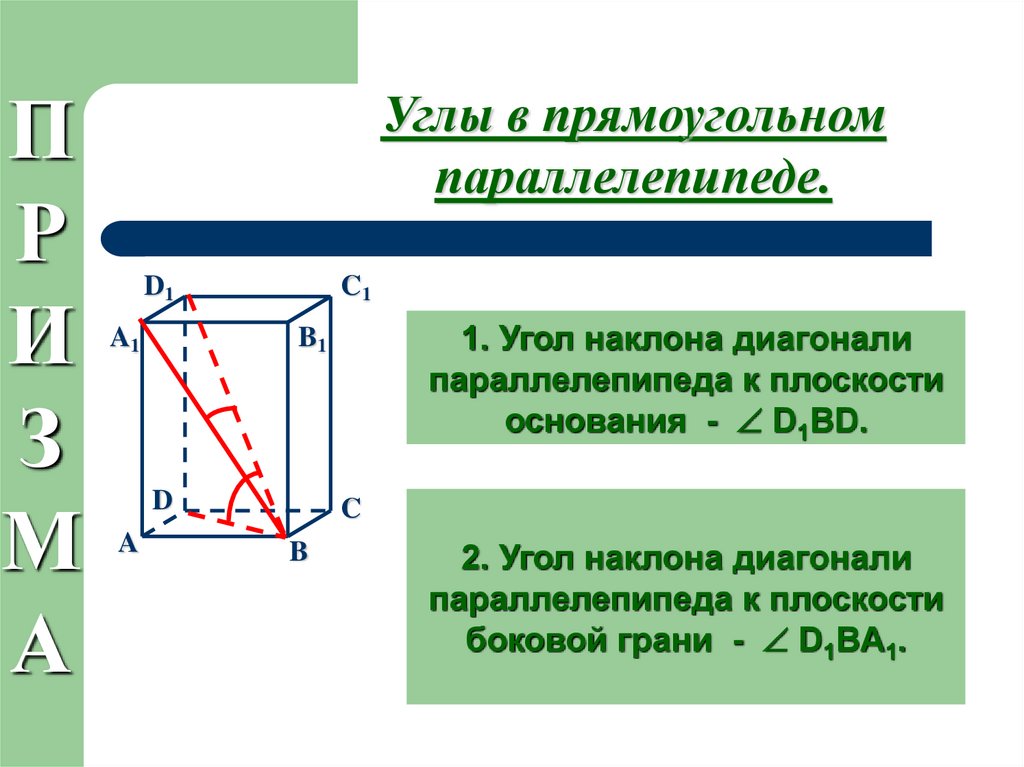
Углы в прямоугольном
параллелепипеде.
D1
A1
C1
D
A
1. Угол наклона диагонали
параллелепипеда к плоскости
основания - D1BD.
B1
C
B
2. Угол наклона диагонали
параллелепипеда к плоскости
боковой грани - D1BА1.

23. Правильная призма

П
Р
И
З
М
А
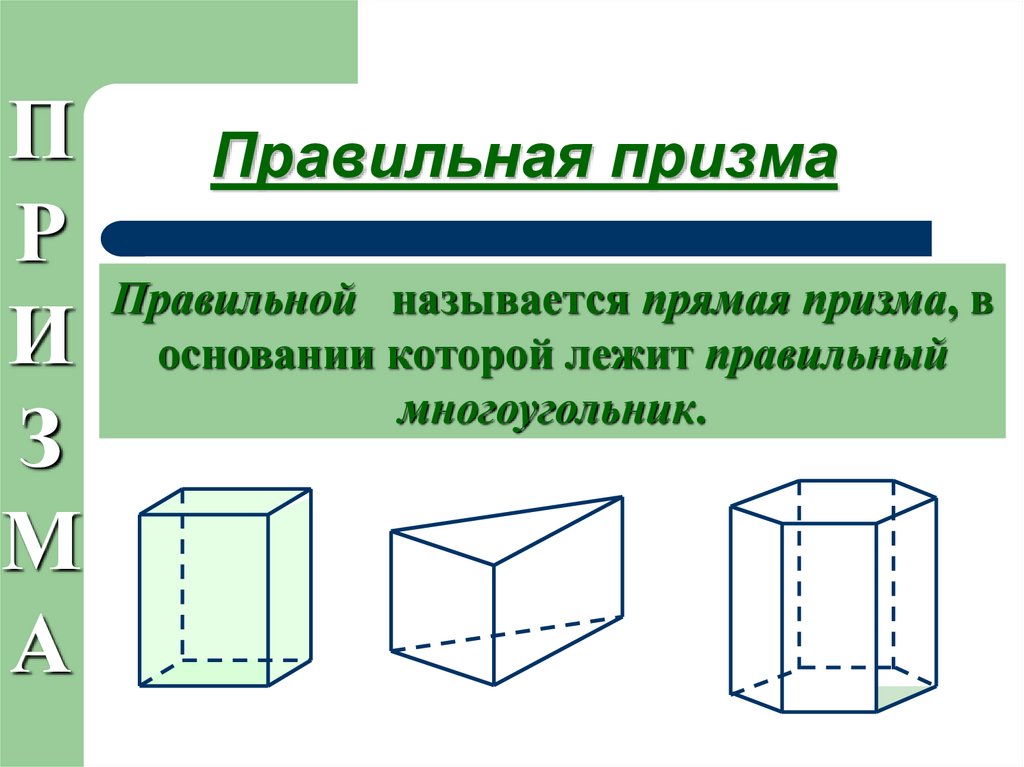
Правильная призма
Правильной называется прямая призма, в
основании которой лежит правильный
многоугольник.

24. Площади полной и боковой поверхностей призмы. Объём призмы.

П
Р
И
З
М
А
Площади полной и боковой
поверхностей призмы.
Объём призмы.
1.
Площадью полной поверхности призмы называется
сумма площадей всех её граней.
2. Площадью боковой поверхности призмы называется
сумма площадей её боковых граней.
3. Для любой призмы Sполн. = Sбок. + 2 Sосн.
4. Для прямой призмы площадь боковой
поверхности равна произведению периметра
основания на высоту Sбок. = Росн. Н
5. Для любой призмы объём равен произведению
площади основания на высоту V = Sосн. Н

25.

П
Р
И
З
М
А
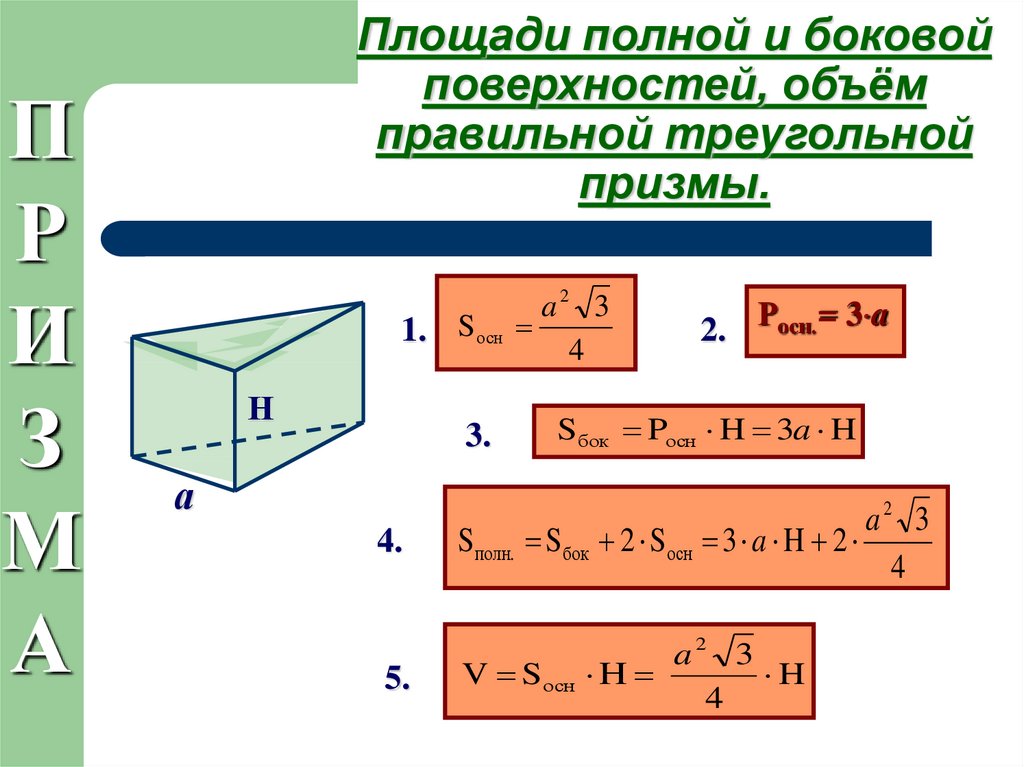
Площади полной и боковой
поверхностей, объём
правильной треугольной
призмы.
1. S осн
Н
3.
а
4.
5.
Sполн.
a2 3
4
2. Росн.= 3 a
Sбок Pосн H 3a H
a2 3
Sбок 2 Sосн 3 a H 2
4
V S осн
a2 3
Н
H
4

26.

П
Р
И
З
М
А
Площади полной и боковой
поверхностей, объём
правильной
четырехугольной призмы.
D1
C1
A1
B1
2
S
=
a
осн
1.
Н
3.
D
A
C
а
B
2. Росн.= 4 a
Sбок Pосн H 4a H
4.
Sполн. Sбок 2 Sосн 4 a H 2 a 2
5.
V Sосн Н a 2 H

27.

П
Р
И
З
М
А
Площади полной и боковой
поверхностей, объём
правильной
шестиугольной призмы.
а
Н
1.
S осн
2.
Росн.= 6 a
3.
4.
Sполн.
a2 3 3 a2 3
6
4
2
Sбок Pосн H 6a H
3 a2 3
Sбок 2 Sосн 6 a H 2
6 a H 3 a2 3
2
5.
V S осн
3a 2 3
Н
H
2

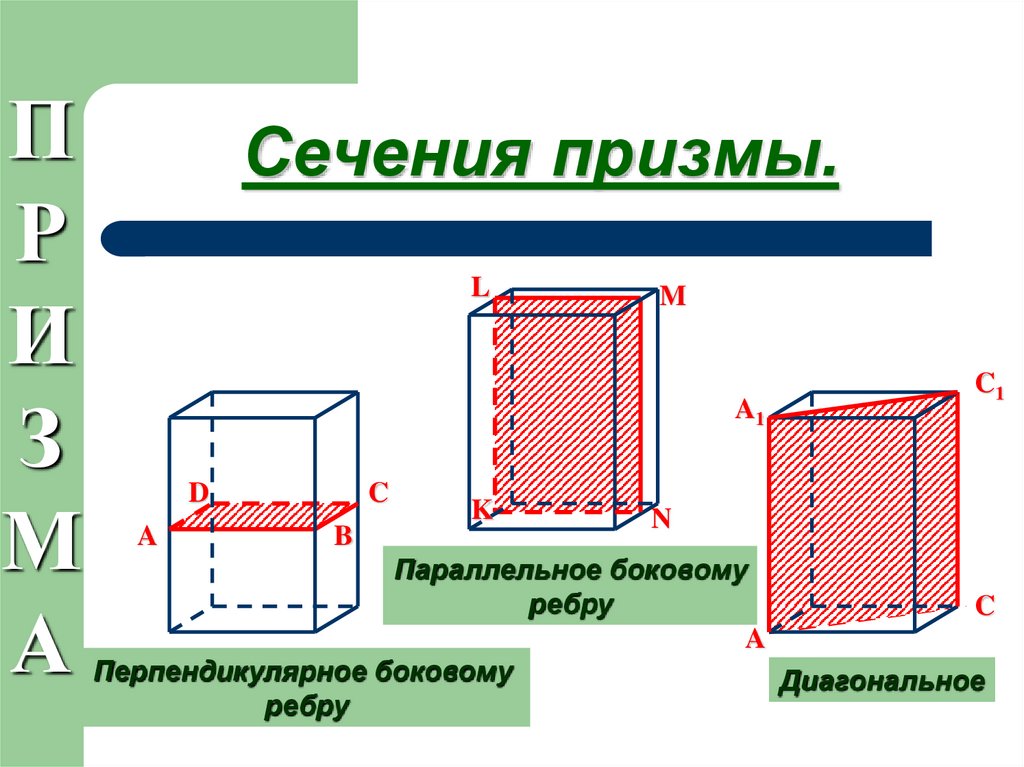
28. Сечения призмы.

П
Р
И
З
М
А
Сечения призмы.
L
M
A1
D
A
C
B
K
C1
N
Параллельное боковому
ребру
C
A
Перпендикулярное боковому
Диагональное
ребру

29.

П
Р
И
З
М
А
Домашнее
задание.
• Выучить теорию по
лекции и учебнику.
• Задачи: учебник
стр.64 №230, 231.