Similar presentations:
Призма
1. призма
2. Призма – многогранник, состоящий из двух многоугольников, совмещаемых параллельным переносом
и всех отрезков соединяющих соответствующиеточки этих многоугольников
В
АВСД и А1В1С1Д1 –
основания
С
А
Д
С1
В1
А1
Д1
3. Призма
Прямая призмаНаклонная призма
4. Наклонная призма
Боковая граньBLMC –
параллелограмм
(ребра
KA║PE║ND║MC║LB)
KR - высота
РВ - диагональ
5. Прямая призма
С1В1
С1
Д1
А1
А1
В
А
В1
С
Д
Д1
В
С
А
Д
Все боковые грани –
прямоугольники
Высота призмы равна
боковому ребру
грань АА1Д1Д –
прямоугольник
h = АА1
6. Правильная призма – это прямая призма, в основании которой правильный многоугольник
• Правильный многоугольник – этомногоугольник, у которого все стороны
и углы равны.
90°
60°
60°
60°
7. Правильная призма
В1В
А
С1
С
Д
А1
В
С
С1
А1
Д1
АВСД - квадрат
h = АА1
А
АВС –равносторонний
треугольник
h = АА1
8.
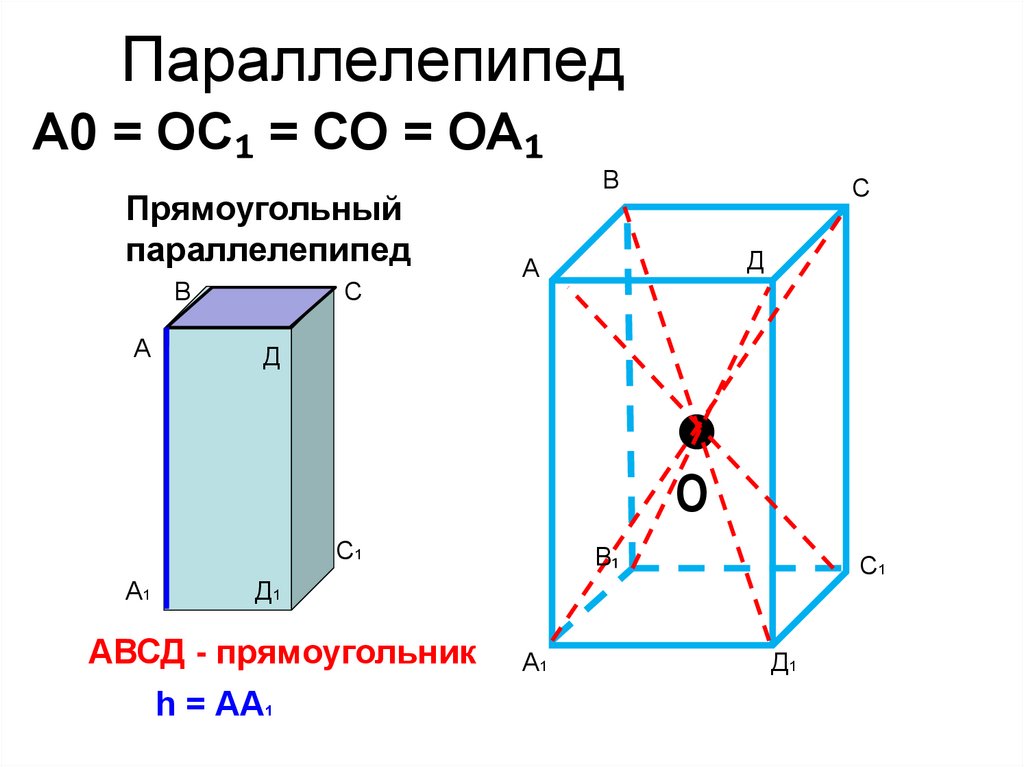
Параллелепипед9. Параллелепипед
А0 = ОС₁ = СО = ОА₁Прямоугольный
параллелепипед
В
А
С
В
С
Д
А
Д
О
С1
А1
В₁
С1
Д1
АВСД - прямоугольник
h = АА1
А1
Д1
10.
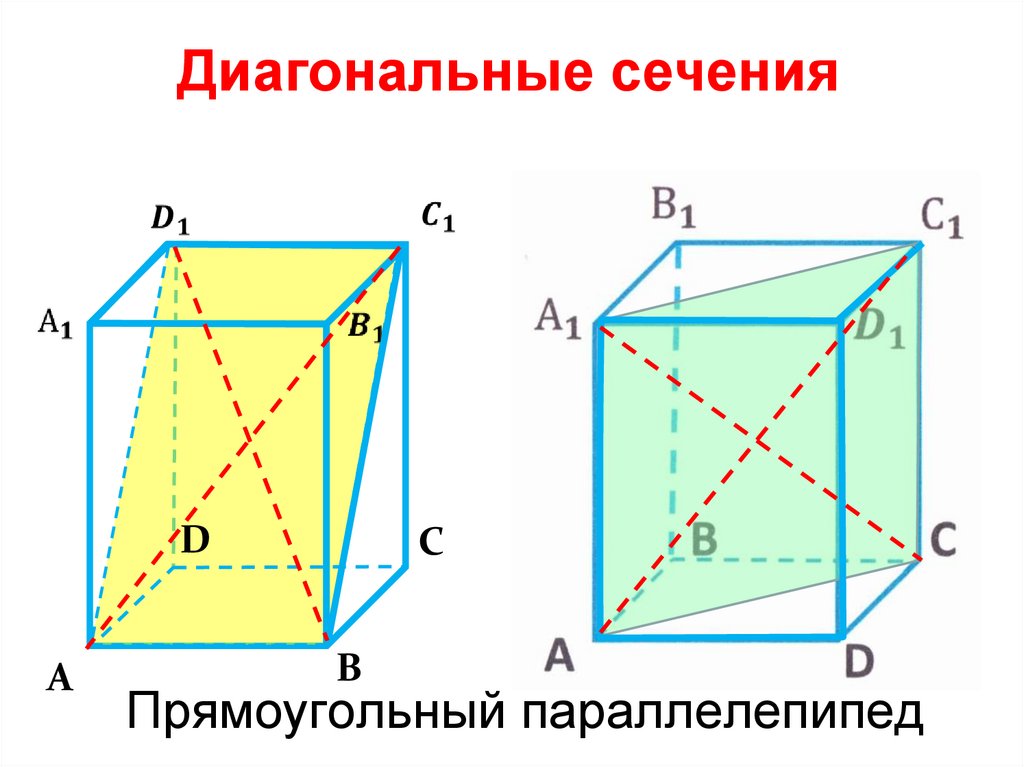
Диагональные сеченияD
А
С
В
Прямоугольный параллелепипед
11.
наклоннаяПрямая
правильная
12. Площадь поверхности призмы
С1В1
А1
Д1
h
С
В
sосн
А
Д
Площадь боковой
поверхности
Sбок = Pосн · h
Площадь полной
поверхности
Sполн = Sбок + 2 Sосн
Объем
V =Sосн · h
13. Призма. Решение задач
Подготовка к ЕГЭ14. Объем куба равен 8. Найдите площадь его поверхности.
С1В1
Д1
А1
В
А
V = a³
Sполн = 6a²
С
Д
8 = a³, а = 2
а – ребро куба
Sполн = 6·2² = 24
Все грани – квадраты
15. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота -10.
Найдите площадь боковойповерхности правильной
шестиугольной призмы, сторона
основания которой равна 5, а высота 10.
Sбок=
Sбок=30P·осн10· =h300
Росн = 6а = 6 · 5 = 30
16. 1. Найдите расстояние между вершинами А и D1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3.
B1C1
4
A1
D1
3
B
C
5
A
4
D
Ответ: 5
17. 2. Найдите квадрат расстояния между вершинами С и А1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3.
B1C1
A1
d² = a² + b² + c²
D1
d² = 4² + 5² + 3²
d² = 16+ 25 + 9
d
c= 3
B
C
5
41
A
a=4
D
5 =b
Ответ: 50
18.
Угол между прямой и плоскостьюВ
А
С
α
19.
Теорема о трех перпендикулярахА
П-р
N
В
M
П-я
С
Угол между плоскостями
20. 3. Найдите угол ABD1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3. Ответ дайте в градусах.
3. Найдите угол ABD1 прямоугольногопараллелепипеда, для которого АВ = 5 , AD = 4 ,
A1AA1 = 3. Ответ дайте в градусах.
B1
C1
D1
3
3
5
A 5
B
4
D
C
Ответ: 45°
21. 4. Найдите угол С1ВС прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 4.
B1A1
C1
D1
4
4
B
4
5
Ответ: 45°
A
C
4
D
22. 5. Найдите угол ДВД1 прямоугольного параллелепипеда, для которого АВ = 4 , AD = 3 , AA1 = 5.
B1A1
D1
5
5
B
C
4
Ответ: 45°
5
A
C1
3
D
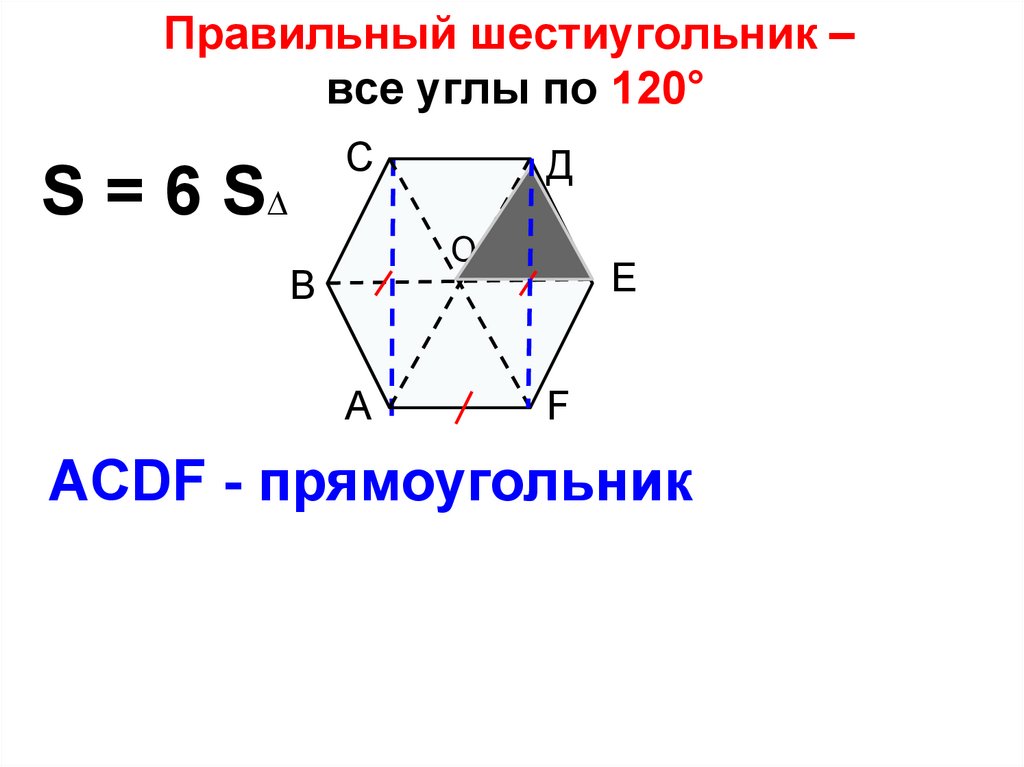
23. Правильный шестиугольник – все углы по 120°
СS = 6 S∆
Д
О
В
А
Е
F
ACDF - прямоугольник
24. 6. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками B и E.
E1
O
1
B
1
Ответ: 2
1





















 mathematics
mathematics








