Готовимся к ЕГЭ. Комбинация: призма - пирамида

1. Готовимся к ЕГЭ. Прототипы В9, В11. Комбинация: призма - пирамида.

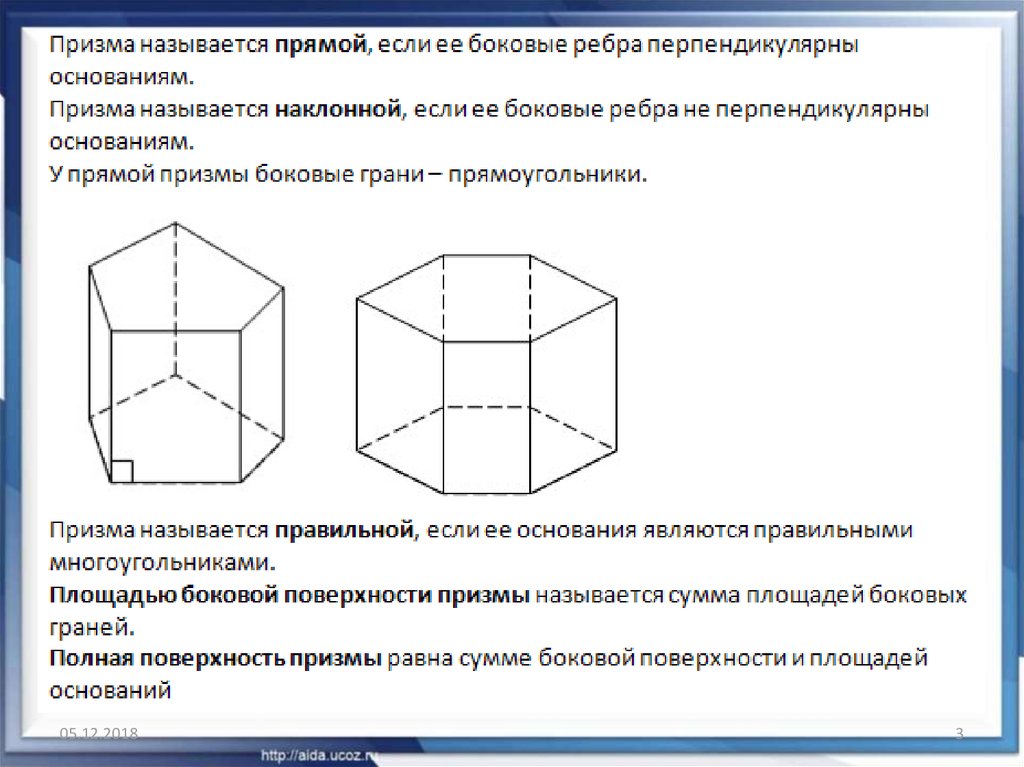
2.

2

3.

05.12.2018
3

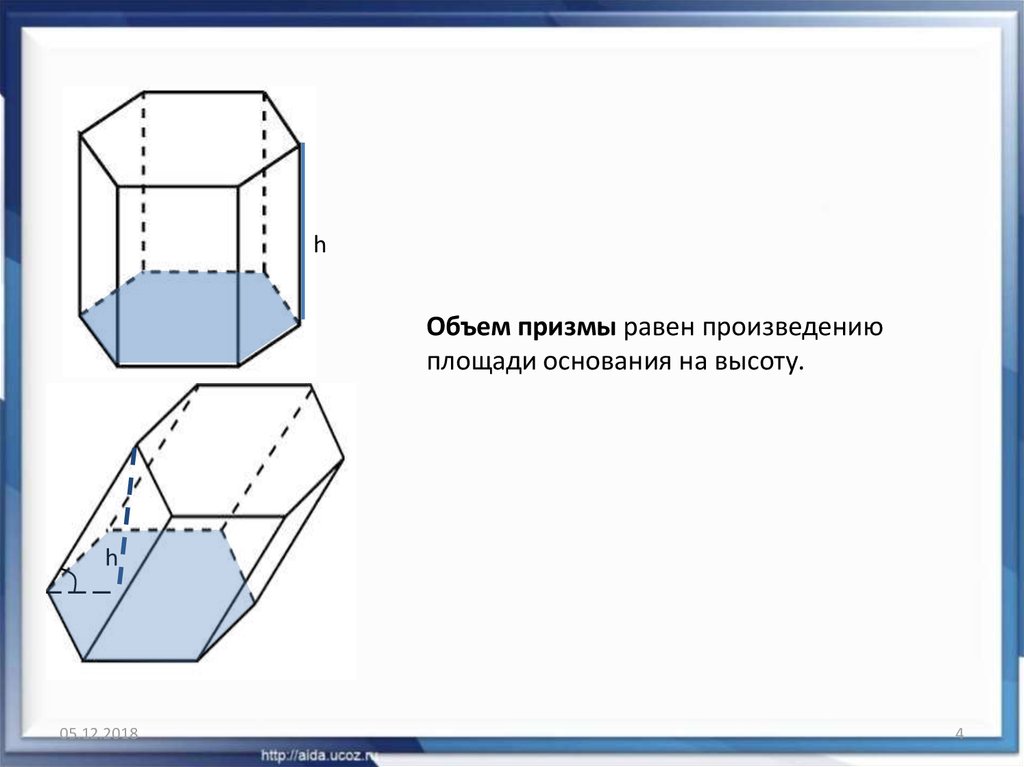
4.

h
Объем призмы равен произведению
площади основания на высоту.
h
05.12.2018
4

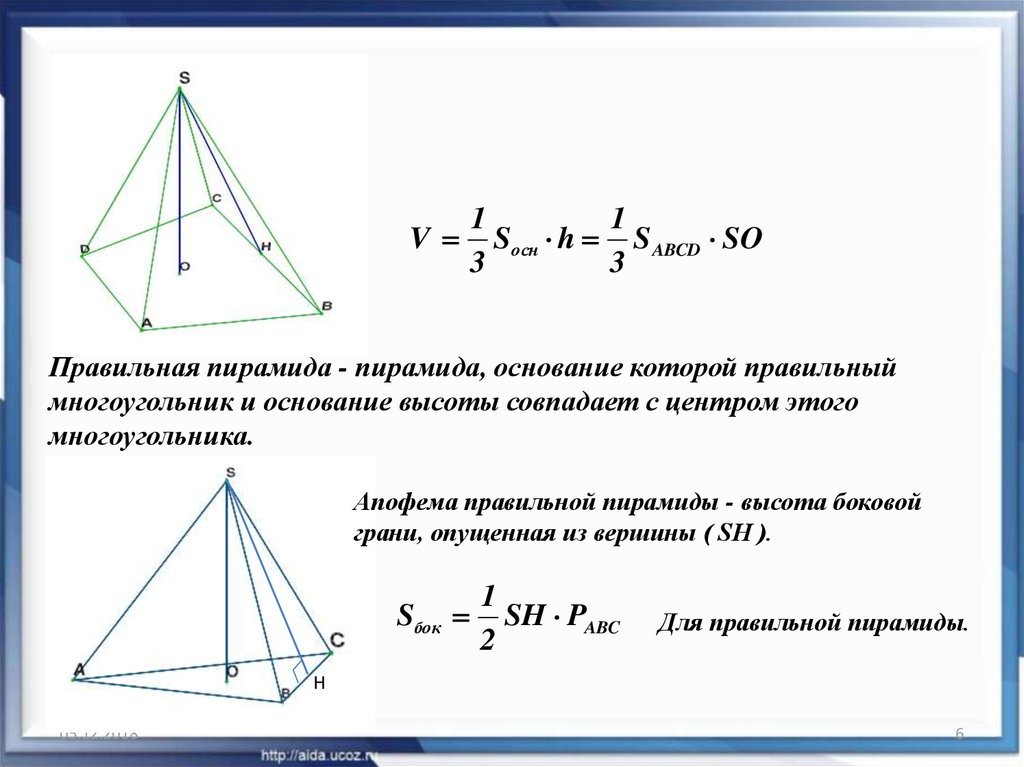
5.

Пирамидой называется многогранник, основанием которой является
многоугольник, а боковые грани - треугольники, имеющие общую
точку. Общая точка является вершиной пирамиды.
Отрезки, соединяющие вершину пирамиды с вершинами основания
называются боковыми ребрами.
Высотой пирамиды является перепендикуляр, опущенный из вершины
на плоскость основания ( SO ).
05.12.2018
5

6.

V
1
1
Sосн h S ABCD SO
3
3
Правильная пирамида - пирамида, основание которой правильный
многоугольник и основание высоты совпадает с центром этого
многоугольника.
Апофема правильной пирамиды - высота боковой
грани, опущенная из вершины ( SH ).
Sбок
1
SH PABC
2
Для правильной пирамиды.
H
05.12.2018
6

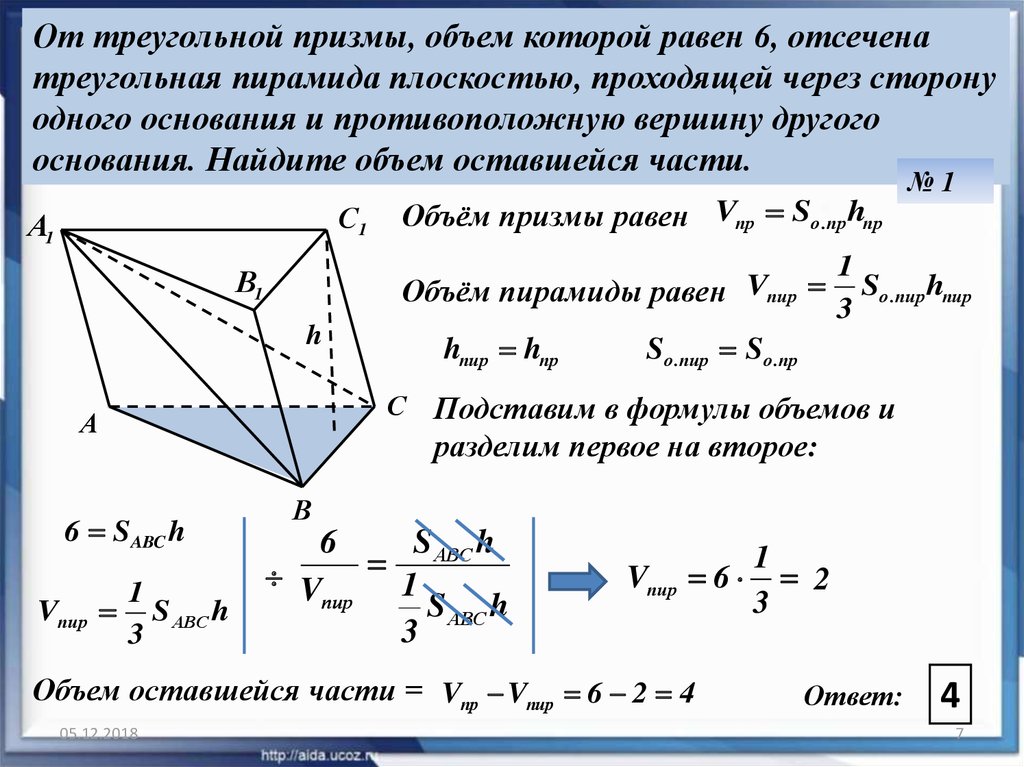
7. От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного

основания и противоположную вершину другого
основания. Найдите объем оставшейся части.
С1
А1
Объём пирамиды равен Vпир
В1
h
hпир hпр
1
Sо .пир hпир
3
Sо .пир Sо .пр
С Подставим в формулы объемов и
А
разделим первое на второе:
6 SABC h
Vпир
Объём призмы равен Vпр Sо .пр hпр
№1
1
S АВС h
3
В
6
S АВС h
V
1
пир
S АВС h
3
Vпир
1
6 2
3
Объем оставшейся части = Vпр Vпир 6 2 4
05.12.2018
Ответ:
4
7

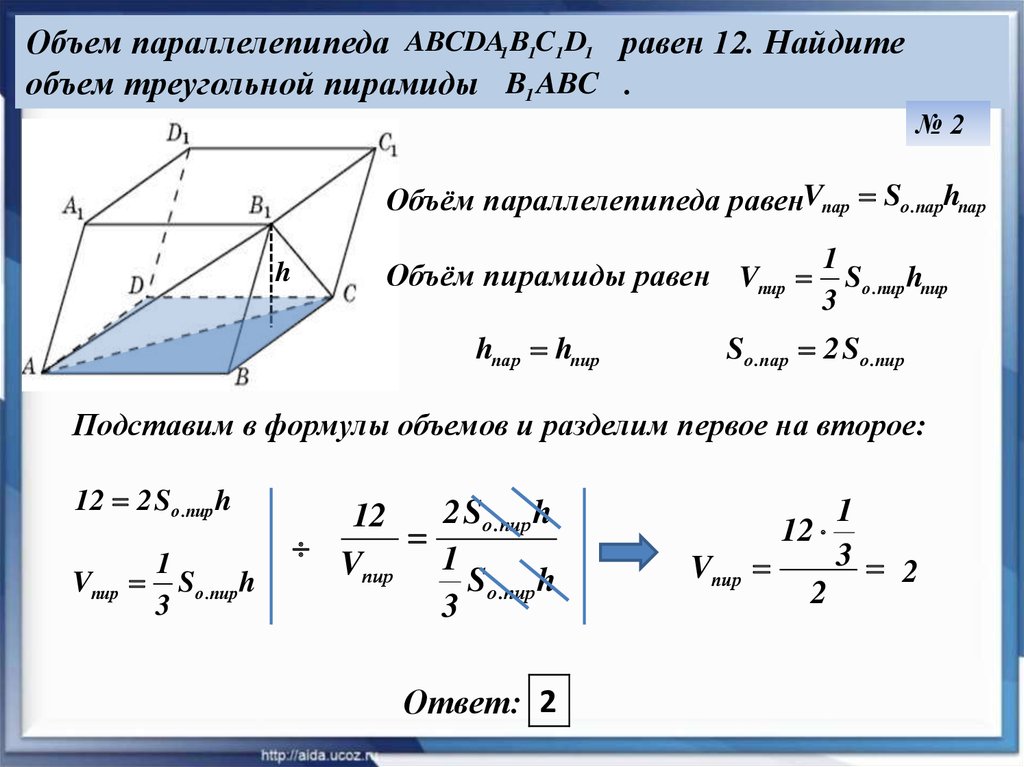
8.

Объем параллелепипеда ABCDA1 B1C1 D1 равен 12. Найдите
объем треугольной пирамиды B1 ABC .
№2
Объём параллелепипеда равенVпар Sо .парhпар
h
Объём пирамиды равен Vпир
hпар hпир
1
Sо .пир hпир
3
Sо .пар 2 Sо .пир
Подставим в формулы объемов и разделим первое на второе:
12 2 Sо .пир h
Vпир
1
Sо .пир h
3
2 Sо .пир h
12
Vпир 1 S h
о .пир
3
Ответ: 2
Vпир
1
12
3 2
2

9.

Найдите объем параллелепипеда ABCDA1 B1C1 D1 , если объем
треугольной пирамиды B1 ABC равен 3 .
№3
Объём параллелепипеда равенVпар Sо .парhпар
Объём пирамиды равен Vпир
h
hпар hпир
1
Sо .пир hпир
3
Sо .пар 2 Sо .пир
Подставим в формулы объемов и разделим первое на второе:
Vпар 2 Sо .пир h
1
3 Sо .пир h
3
Vпар
2 Sо .пир h
1
3
Sо .пир h
3
Vпар
3 2
18
1
3
Ответ: 1 8

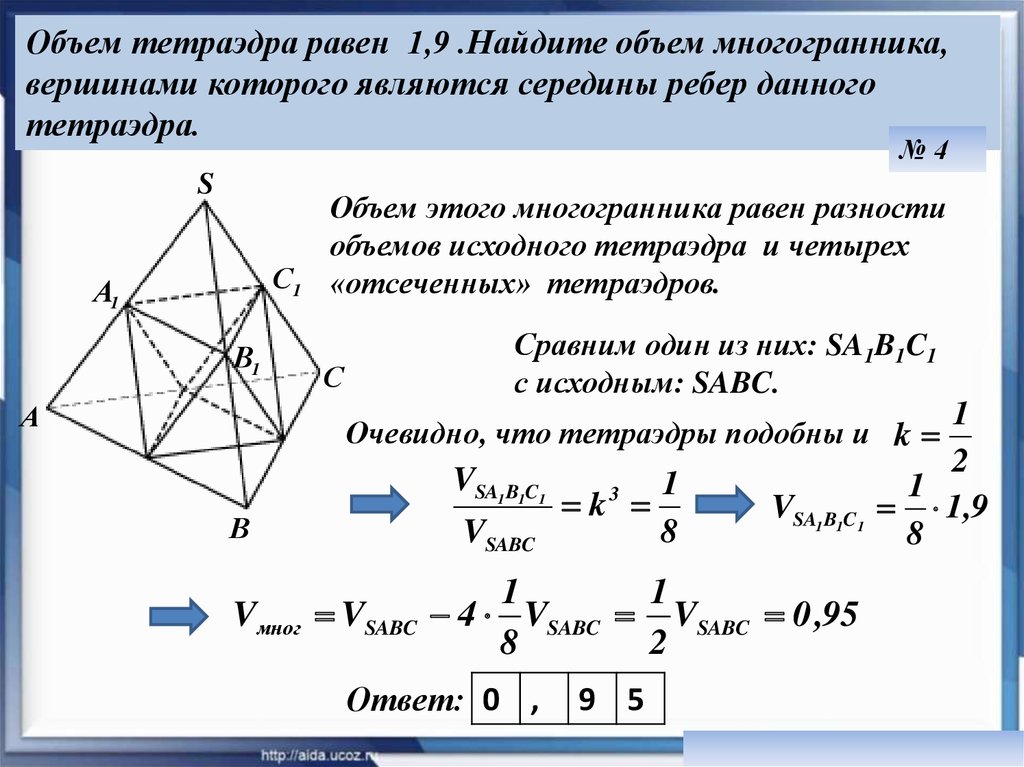
10.

Объем тетраэдра равен 1,9 .Найдите объем многогранника,
вершинами которого являются середины ребер данного
тетраэдра.
№4
S
С1
А1
В1
А
Объем этого многогранника равен разности
объемов исходного тетраэдра и четырех
«отсеченных» тетраэдров.
Сравним один из них: SA1B1C1
с исходным: SABC.
С
1
2
1
1,9
8
Очевидно, что тетраэдры подобны и k
VSA1 B1C1
В
VSABC
Vмног VSABC
1
k
8
3
VSA1 B1C1
1
1
4 VSABC VSABC 0 ,95
8
2
Ответ: 0 ,
9 5

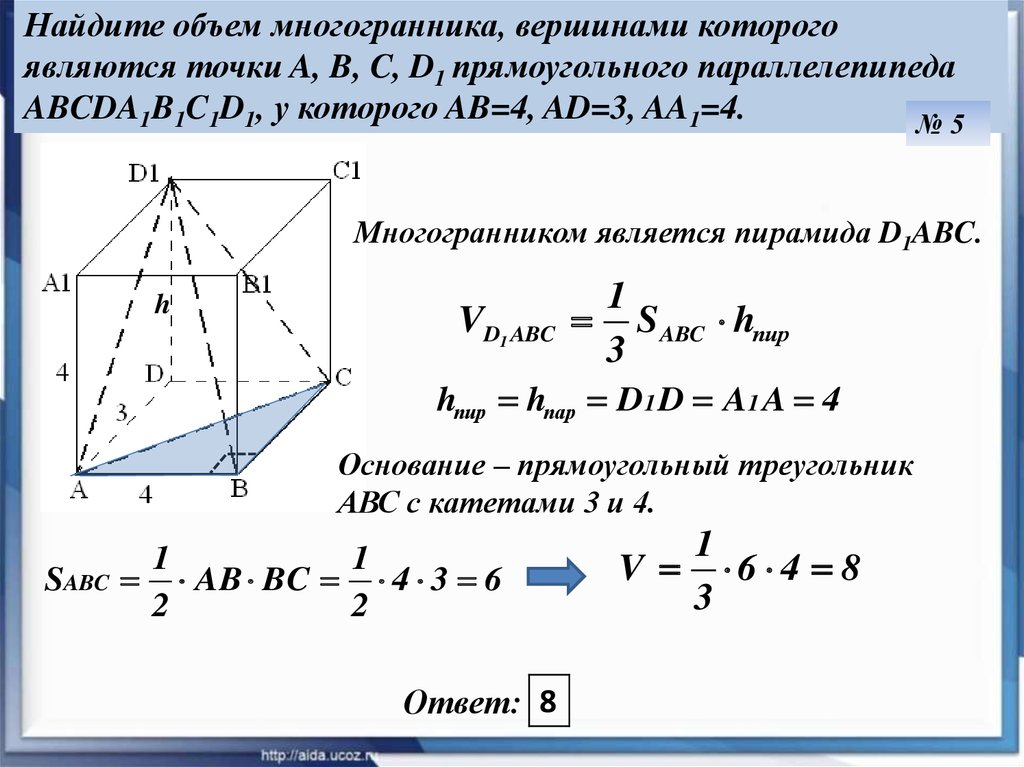
11.

Найдите объем многогранника, вершинами которого
являются точки A, B, C, D1 прямоугольного параллелепипеда
ABCDA1B1C1D1, у которого AB=4, AD=3, AA1=4.
№5
Многогранником является пирамида D1ABC.
h
VD1 ABC
1
S ABC hпир
3
hпир hпар D 1 D A1 A 4
Основание – прямоугольный треугольник
АВС с катетами 3 и 4.
SABC
1
1
AB BC 4 3 6
2
2
Ответ: 8
1
V 6 4 8
3

12.

Найдите объем многогранника, вершинами которого
являются точки A, B, C, A1 правильной треугольной призмы
ABCA1B1C1, площадь основания которой равна 2, а боковое
ребро равно 3.
№6
Многогранником является пирамида А1ABC.
h
Vпир
1
S АВС h
3
h A1 A 3
SABC 2 ( по условию )
1
V 2 3 2
3
Ответ: 2

13. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Объем куба равен 12. Найдите объем четырехугольной
пирамиды, основанием которой является грань куба, а
вершиной — центр куба.
№7
В
О
А
Куб можно рассматривать, как призму
Объём призмы равен Vпр Sо .пр hпр
1
Объём пирамиды равен Vпир Sо .пир hпир
3
Sо .пир Sо .пр
hпр АВ 2 hпир 2 АО
Подставим в формулы объемов и
разделим первое на второе:
12 Sосн 2ОВ
Vпир
12
Sосн 2ОВ
Vпир 1 S ОВ
1
Sосн ОВ
осн
3
3
05.12.2018
Vпир
12
2
1
3 2
Ответ:
2
13

14.

Объем параллелепипеда АВСDA1B1C1D1 равен 4,5 . Найдите
объем треугольной пирамиды AD1CB1 .
№8
Объем пирамиды AD1CB1 равен разности
VAD1СB1 исходного
Vпар 4VB1параллелепипеда
объемов
ABC 4 ,5 4 0 ,75и 1,5
четырех «отсеченных» пирамид.
Сравним одну из них: В1ABC
с исходным параллелепипедом.
h
Объём параллелепипеда равен Vпар Sо .пар ВВ1
Объём пирамиды равен
VВ1 АВС
Sо .пар 2 S АВС
1
S АВС ВВ1
3
Подставим в формулы объемов и разделим первое на второе:
1
4 ,5 2 S АВС h
4 ,5
2 S АВС h
4 ,5
3 0 ,75
V
1
V
В1 АВС
1
В1 АВС
S АВС h
2
VВ АВС S АВС h
1
3
3
Ответ:
1 ,
5

15.

Найдите объем многогранника, вершинами которого являются
точки A, D, А1, В, С, В1 прямоугольного параллелепипеда
ABCDA1B1C1D1, у которого АВ=3, АD=4, АА1=5.
№9
С1 Диагональное сечение А1В1СD делит
прямоугольный параллелепипед на два
равных многогранника.
В1
А1
D1
Объем одного из них требуется найти..
5
В
С
3
А
Vмн
4
AB AD AA1
2
2
Vпар
D
5 3 4
30
2
Ответ: 3 0

16.

Найдите объем многогранника, вершинами которого являются
точки А1, В, С, С1 прямоугольного параллелепипеда
ABCDA1B1C1D1, у которого АВ=4, АD=3, АА1=4.
№ 10
А1
D1
4
А
D
3
4
В
h
В1
С1
С
Лучше всего расположить параллелепипед,
как на рисунке.
Многогранник, объем которого требуется
найти – пирамида A1B1C1СВ.
Пирамида и параллелепипед имеют общее
основание и высоту.
Объём параллелепипеда равен Vпар Sоснh
Объём пирамиды равен
Vпир
1
Sоснh
3
=> Объем пирамиды в три раза меньше объема параллелепипеда
Vпир
1
3 4 4 16
3
Ответ: 1 6

17.

Найдите объем многогранника, вершинами которого являются
точки A, В, С, В1 прямоугольного параллелепипеда
ABCDA1B1C1D1, у которого АВ=3, АD=3, АА1=4.
В1
С1
А1
D1
h
4
В
С
3
А
№ 11
Vпар 3 3 4 36
Многогранник, объем которого требуется
найти – пирамида B1ВАС.
Объём параллелепипеда равен Vпар Sо .парhпар
Объём пирамиды равен
Vпир
1
Sо .пир hпир
3
Sо .пар 2 Sо .пир
hпар hпир
Подставим в формулы объемов и разделим первое на второе:
3
D
36 2 Sо .пир h
Vпир
1
Sо .пир h
3
2 Sо .пир h
36
Vпир 1 S h
о .пир
3
Vпир
36
1
3
6
2
Ответ: 6

18. Найдите объем многогранника, вершинами которого являются точки A, В, С, А1, С1 правильной треугольной призмы ABCA1B1C1, площадь

основания которой равна 3, а боковое
ребро =2.
С1
А1
В1
2
С
А
№ 12
Объем многогранника равен разности
объемов исходной призмы и пирамиды
А1В1С1 .
hпир hпр 2
Sо .пир Sо .пр S A1 B1C1 3
Vпр Sо .пр hпр 3 2 6
В
Vпир
1
1
Sо .пир hпир 3 2 2
3
3
Объем многогранника= Vпр Vпир 6 2 4
Ответ:
05.12.2018
4
18

19. Найдите объем многогранника, вершинами которого являются точки A, В, С, D, E, F, А1 правильной шестиугольной призмы

ABCDEFA1B1C1D1E1F1, площадь основания которой равна 4, а
боковое ребро равно 3.
№ 13
А1
В1
F1
Е1
С1
D1
А
В 3
F
Многогранник, объем которого требуется
найти – пирамида А1АВСDEF.
hпир hпр 3
Sо .пир Sо .пр S A1 B1C1 4
С
Е
D
Vпир
1
1
Sо .пир hпир 4 3 4
3
3
Ответ:
05.12.2018
4
19

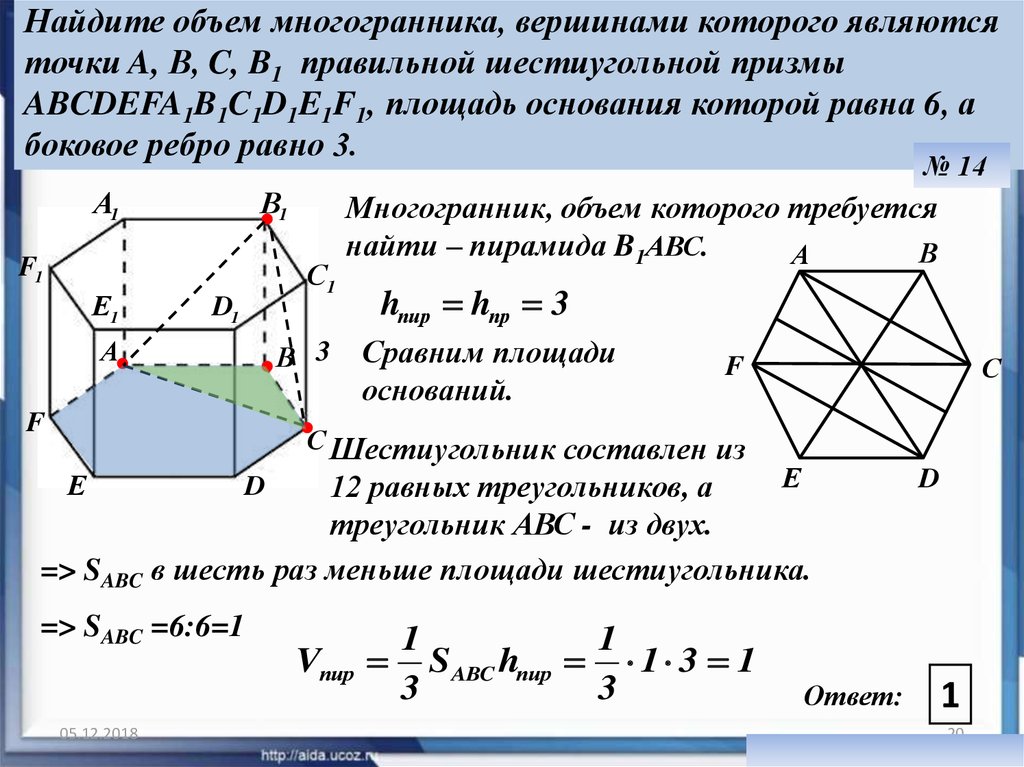
20. Найдите объем многогранника, вершинами которого являются точки A, В, C, B1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1,

площадь основания которой равна 6, а
боковое ребро равно 3.
№ 14
А1
В1
F1
Е1
С1
D1
А
Многогранник, объем которого требуется
найти – пирамида B1АВС.
В
А
В 3
F
hпир hпр 3
Сравним площади
оснований.
С
F
С Шестиугольник составлен из
Е
12 равных треугольников, а
треугольник АВС - из двух.
=> SABC в шесть раз меньше площади шестиугольника.
Е
=> SABC =6:6=1
05.12.2018
D
Vпир
1
1
S ABC hпир 1 3 1
3
3
Ответ:
D
1
20

21. Спасибо за работу.