Призма. Площадь поверхности призмы

1.

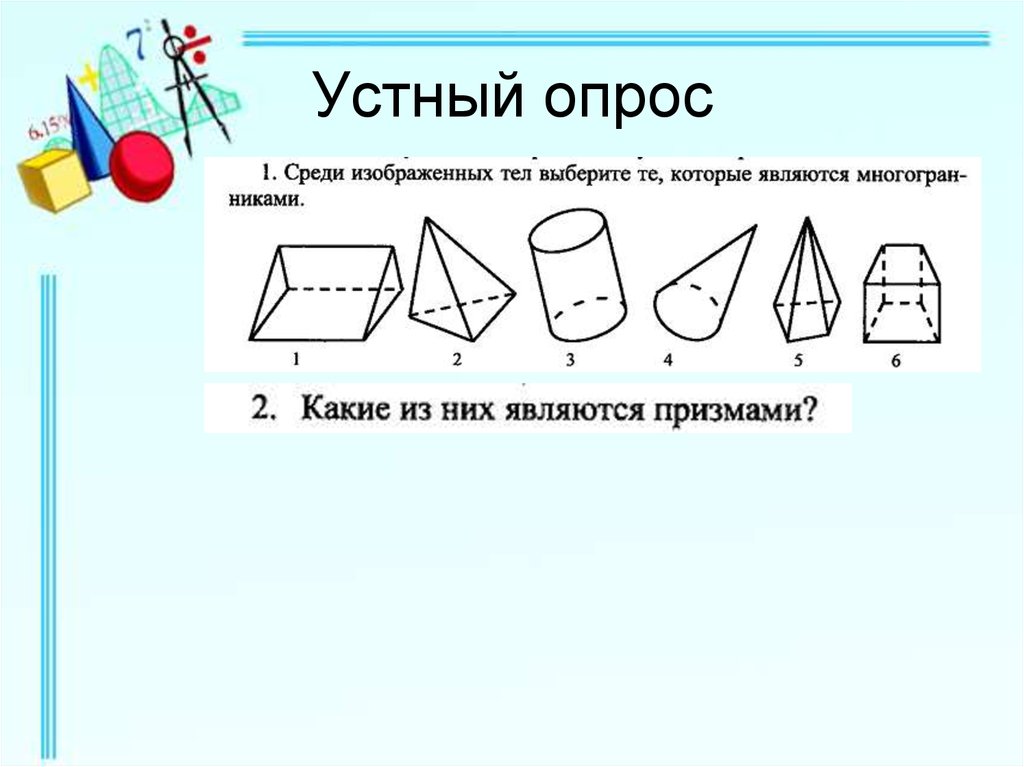
2. Устный опрос

3.

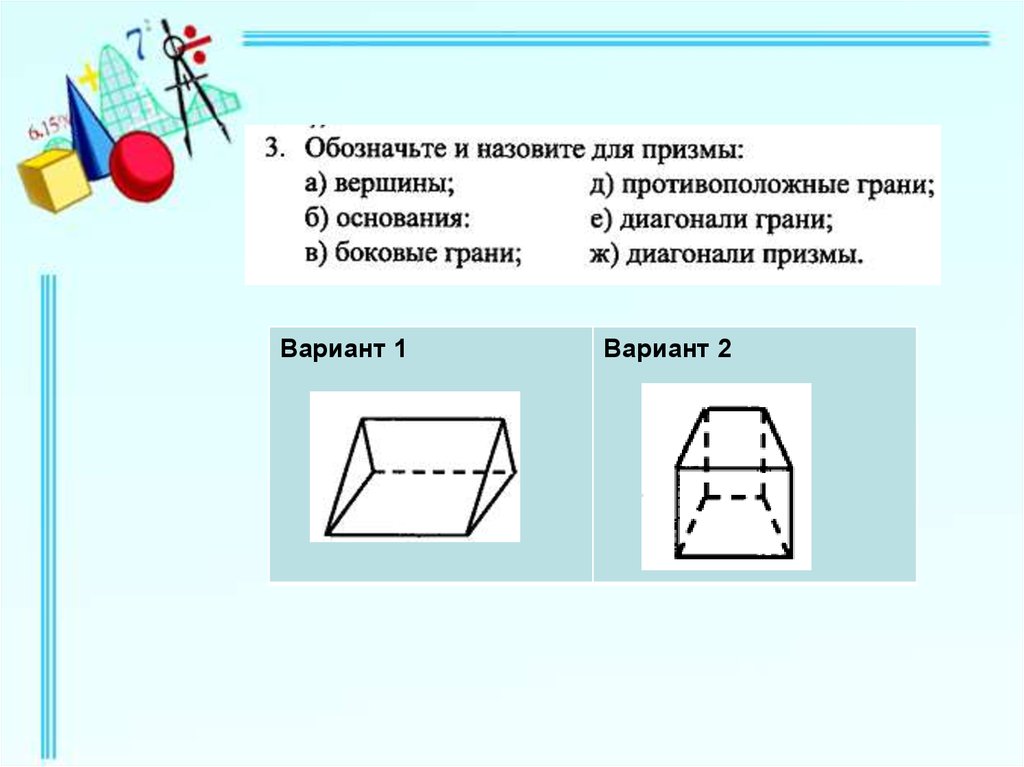
Вариант 1
Вариант 2

4.

5.

6.

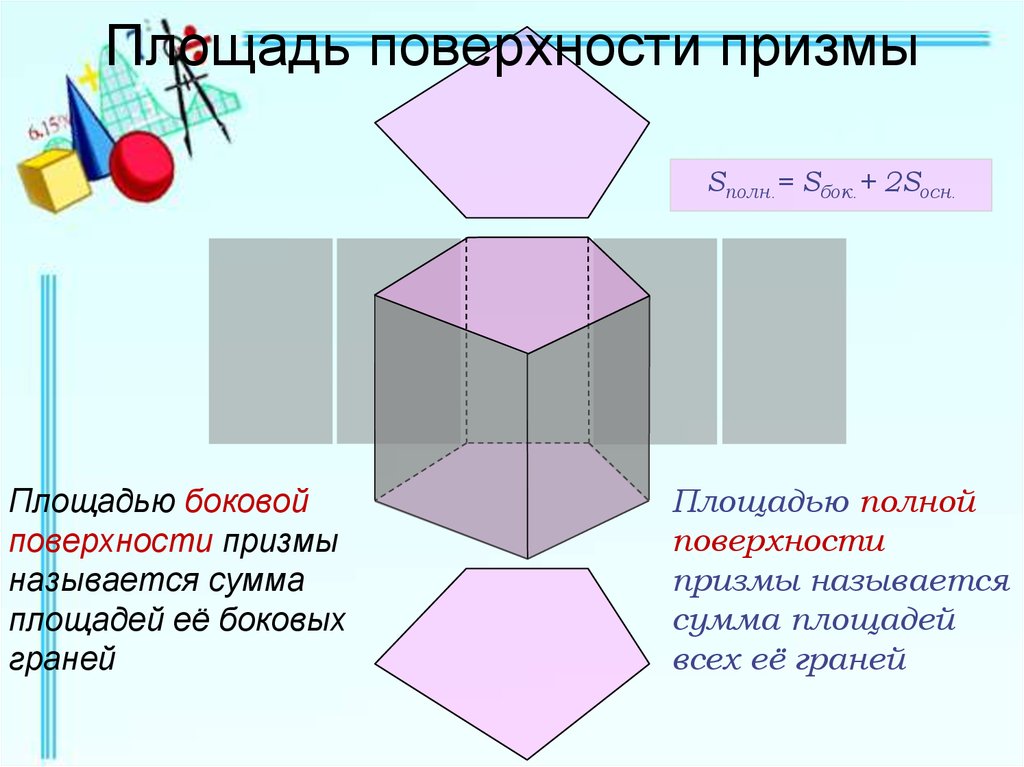
Площадь поверхности призмы
Sполн.= Sбок.+ 2Sосн.
Площадью боковой
поверхности призмы
называется сумма
площадей её боковых
граней
Площадью полной
поверхности
призмы называется
сумма площадей
всех её граней

7. Теорема о площади боковой поверхности прямой призмы

Площадь боковой поверхности прямой призмы
равна произведению периметра основания на
высоту призмы
Sбок. = Росн.· h
Доказательство.
Боковые грани прямой призмы – прямоугольники, основания
которых – стороны основания призмы, а высоты равны высоте
h призмы.
Sбок. = A1A2· h + A2A3· h + A3A4· h + … + An-1An· h =
= (A1A2 + A2A3 + A3A4 + … + An-1An) · h = Pосн.· h

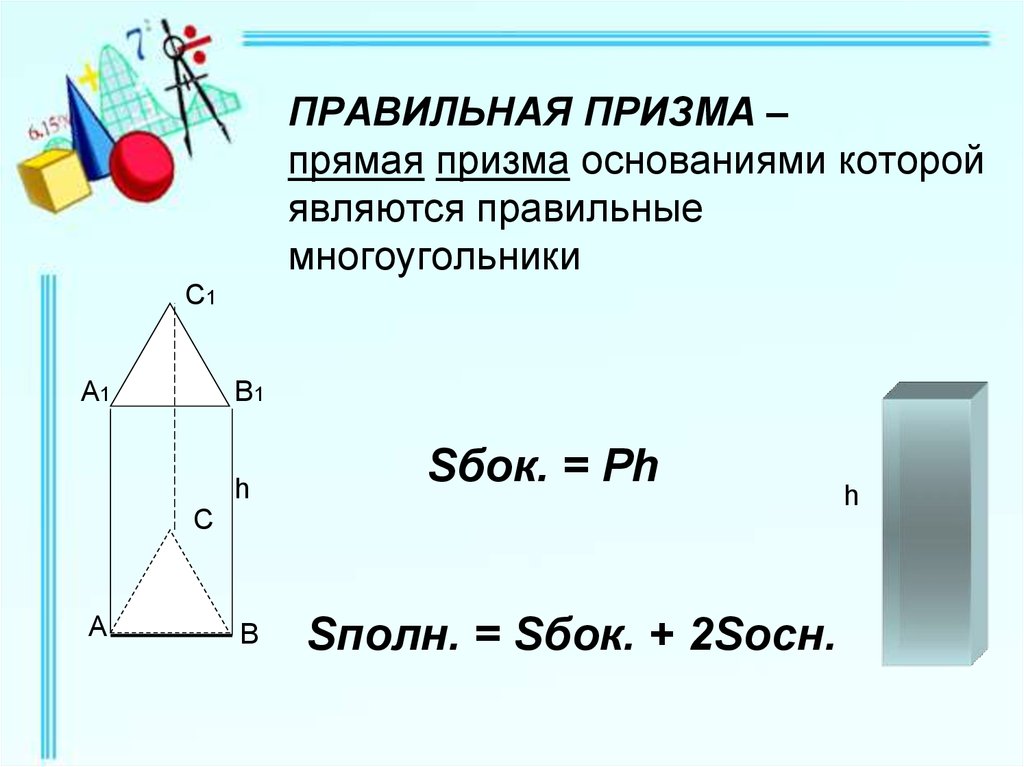
8. ПРАВИЛЬНАЯ ПРИЗМА – прямая призма основаниями которой являются правильные многоугольники

C1
A1
B1
h
Sбок. = Ph
C
A
B
Sполн. = Sбок. + 2Sосн.
h

9.

10.

№ 219.
D1
С1
А1
В1
?
D
С
450
А
12 см
В
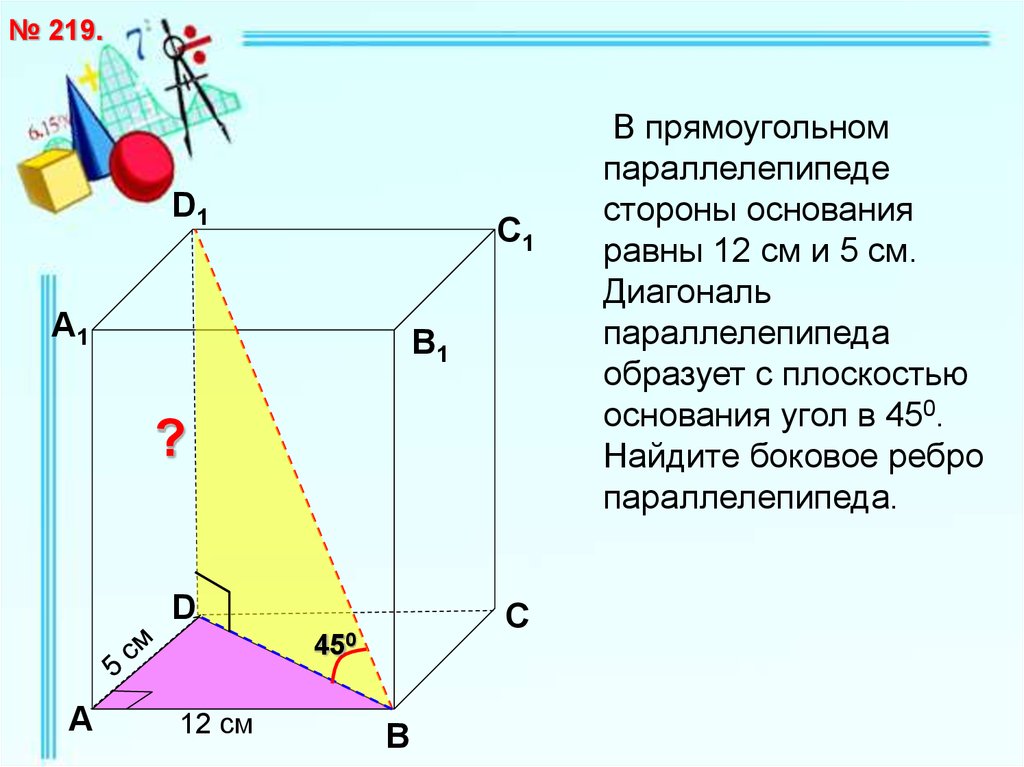
В прямоугольном
параллелепипеде
стороны основания
равны 12 см и 5 см.
Диагональ
параллелепипеда
образует с плоскостью
основания угол в 450.
Найдите боковое ребро
параллелепипеда.

11.

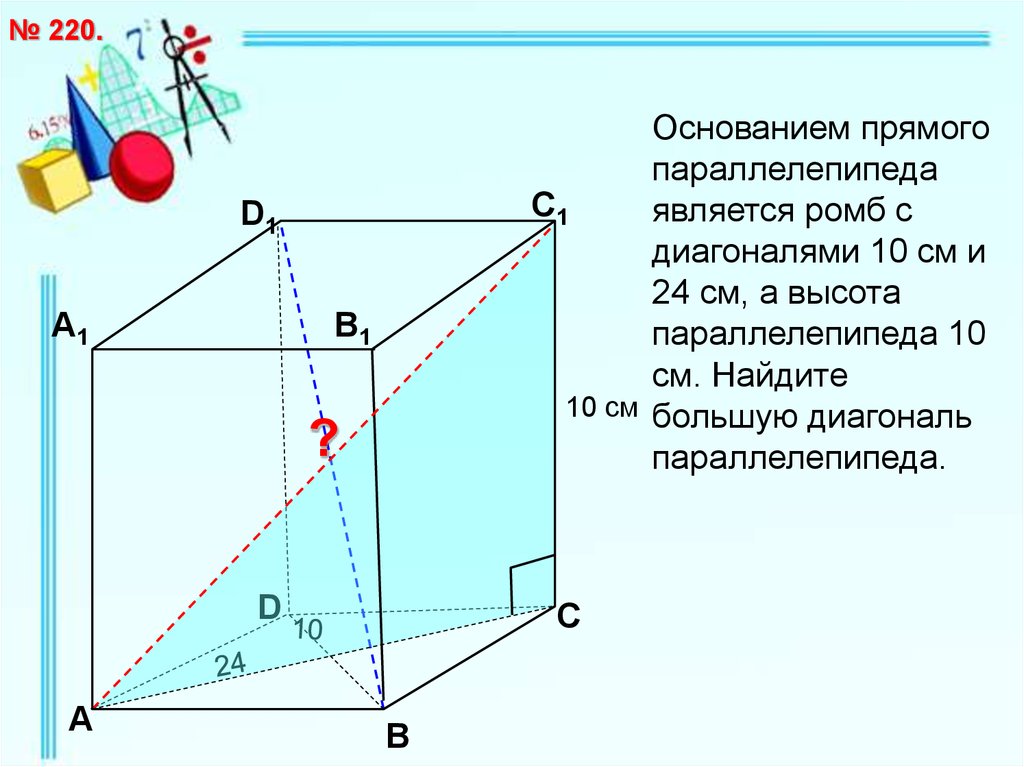
№ 220.
Основанием прямого
параллелепипеда
С1
является ромб с
диагоналями 10 см и
24 см, а высота
параллелепипеда 10
см. Найдите
10 см большую диагональ
параллелепипеда.
D1
А1
В1
?
D
А
С
В

12.

№ 223.
64
D1
С1
В1
А1
a
S=
D
a
А
a
В
С
2
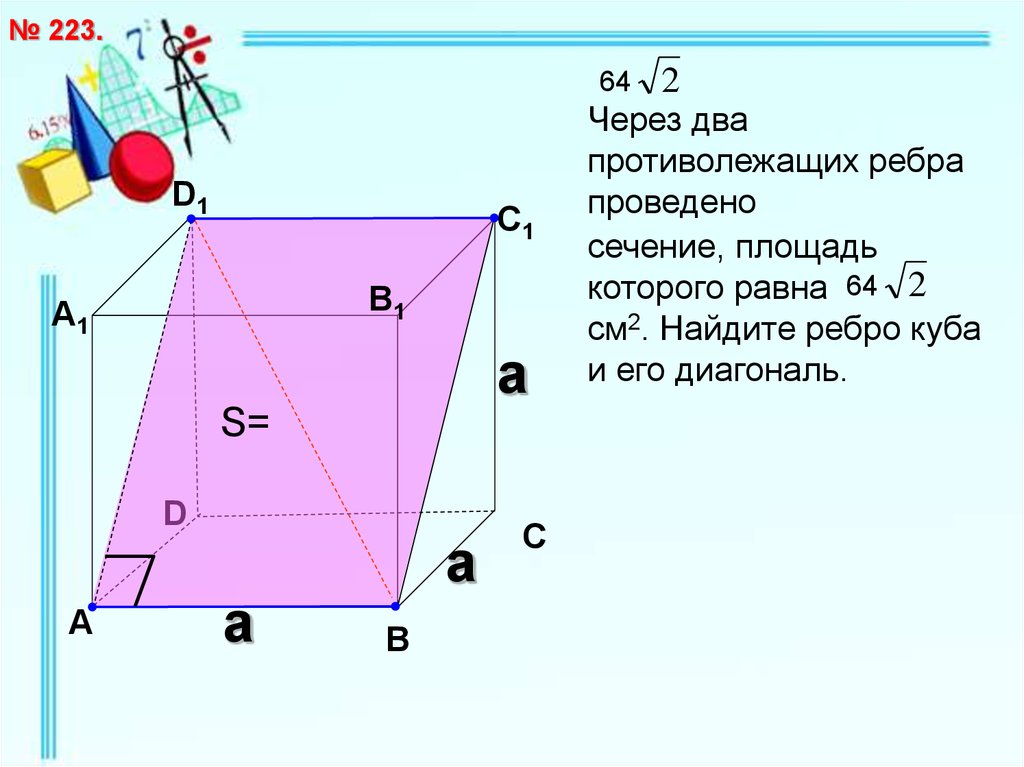
Через два
противолежащих ребра
проведено
сечение, площадь
которого равна 64 2
см2. Найдите ребро куба
и его диагональ.