Призма. Поверхность призмы. Параллелепипед. Куб. Поверхность параллелепипеда

1. Призма. Поверхность призмы. Параллелепипед. Куб. Поверхность параллелепипеда.

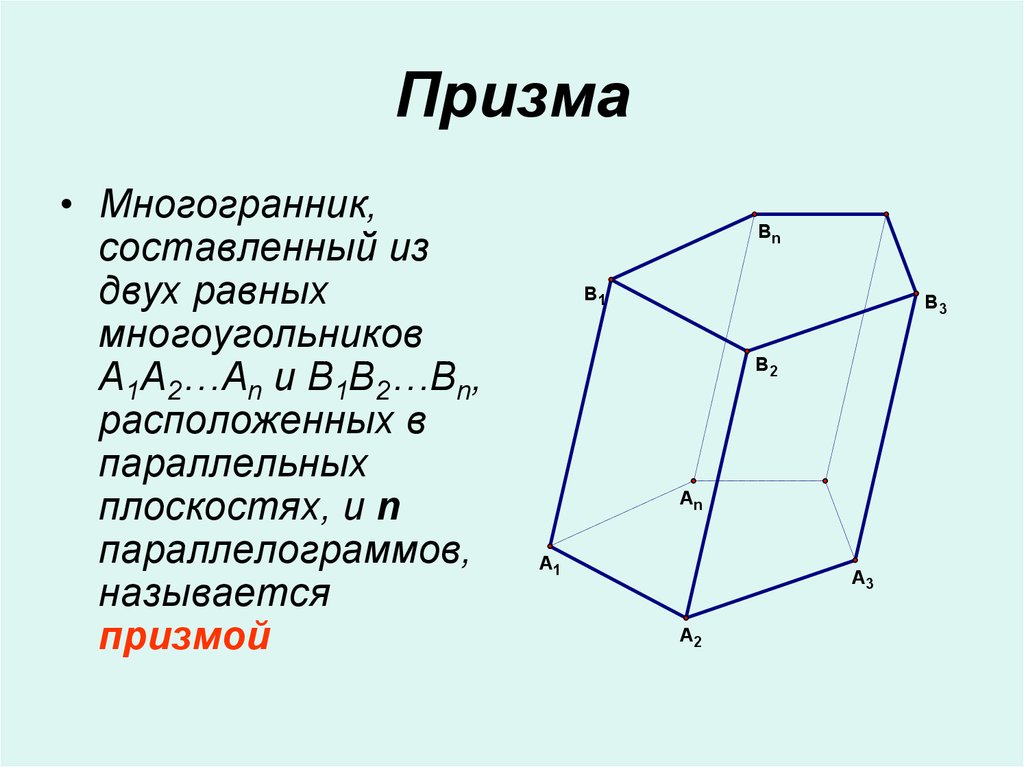
2. Призма

• Многогранник,
составленный из
двух равных
многоугольников
A1A2…An и B1B2…Bn,
расположенных в
параллельных
плоскостях, и n
параллелограммов,
называется
призмой
Bn
B1
B3
B2
An
A1
A3
A2

3.

Bn
B1
B3
B2
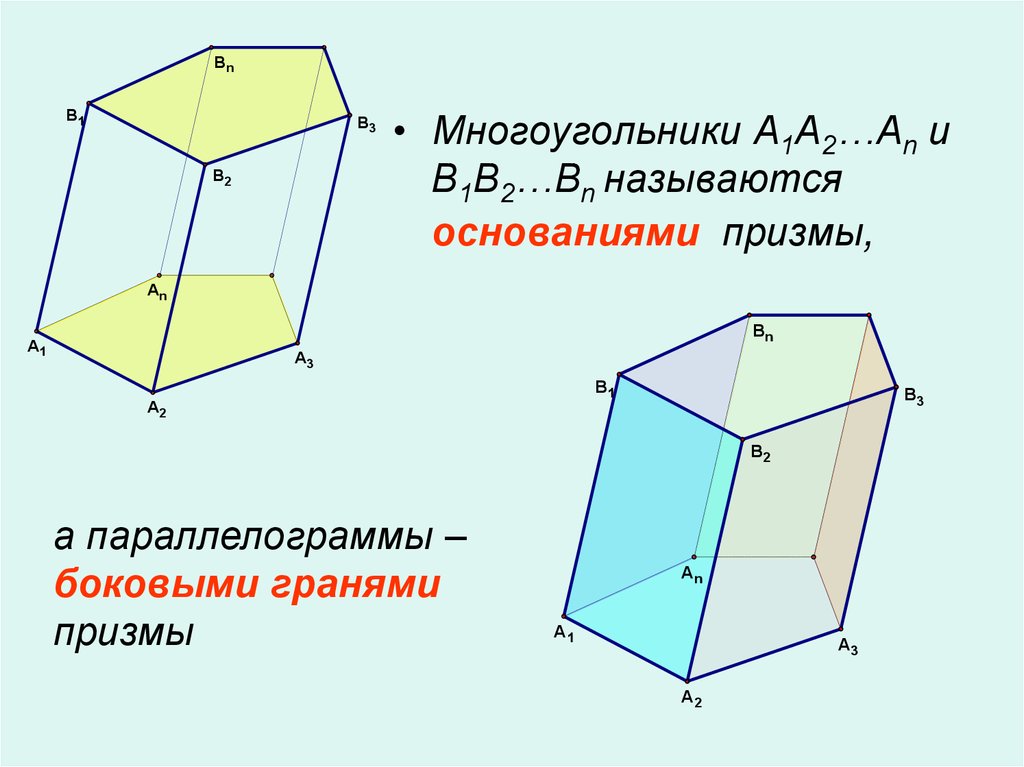
• Многоугольники A1A2…An и
B1B2…Bn называются
основаниями призмы,
An
Bn
A1
A3
B1
B3
A2
B2
а параллелограммы –
боковыми гранями
призмы
An
A1
A3
A2

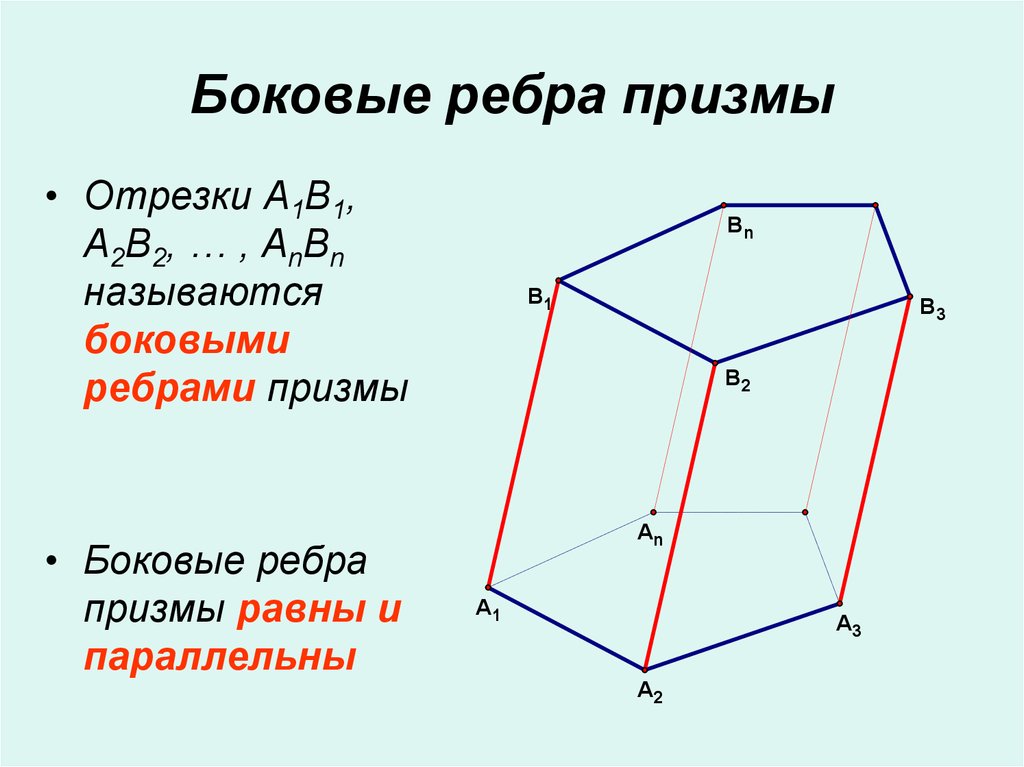
4. Боковые ребра призмы

• Отрезки A1B1,
A2B2, … , AnBn
называются
боковыми
ребрами призмы
• Боковые ребра
призмы равны и
параллельны
Bn
B1
B3
B2
An
A1
A3
A2

5.

• Призму с основаниями A1A2…An и
B1B2…Bn обозначают A1A2…AnB1B2…Bn и
называют n-угольной призмой

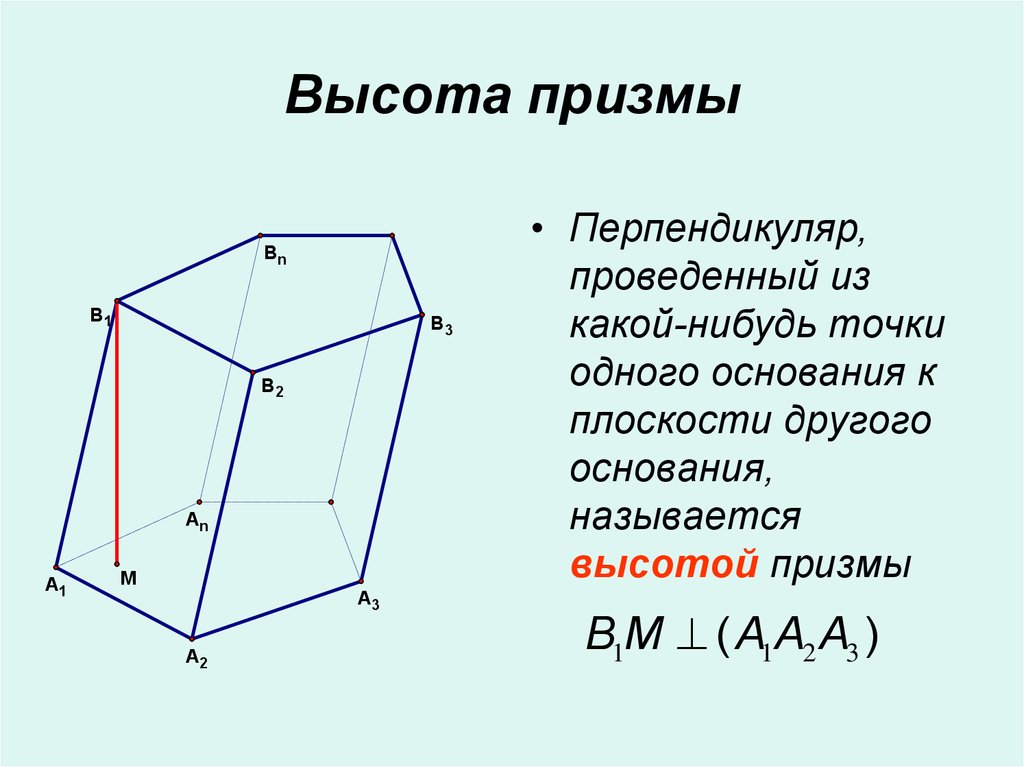
6. Высота призмы

Bn
B1
B3
B2
An
A1
M
A3
A2
• Перпендикуляр,
проведенный из
какой-нибудь точки
одного основания к
плоскости другого
основания,
называется
высотой призмы
B1M ( A1A2 A3 )

7.

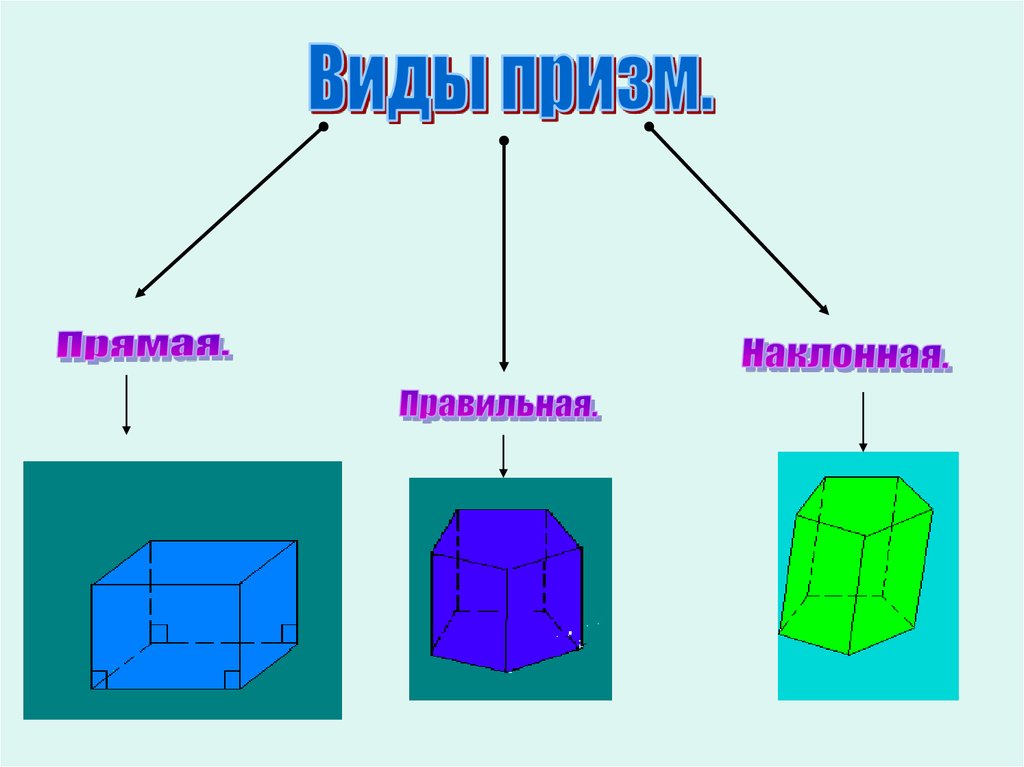
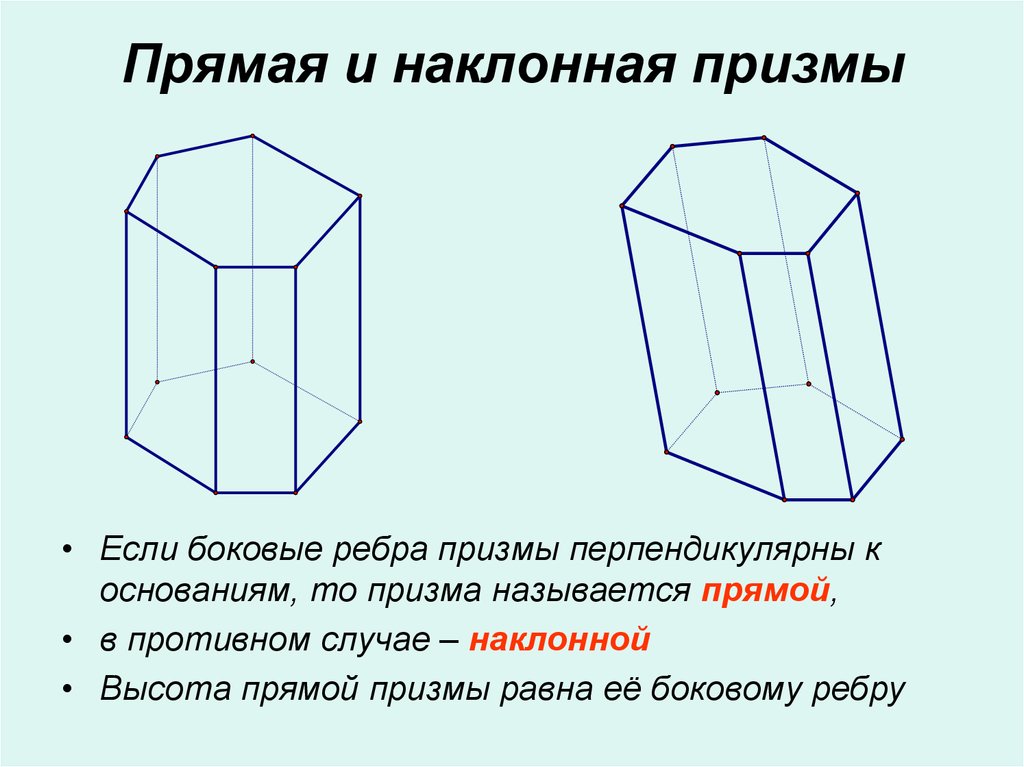
8. Прямая и наклонная призмы

• Если боковые ребра призмы перпендикулярны к
основаниям, то призма называется прямой,
• в противном случае – наклонной
• Высота прямой призмы равна её боковому ребру

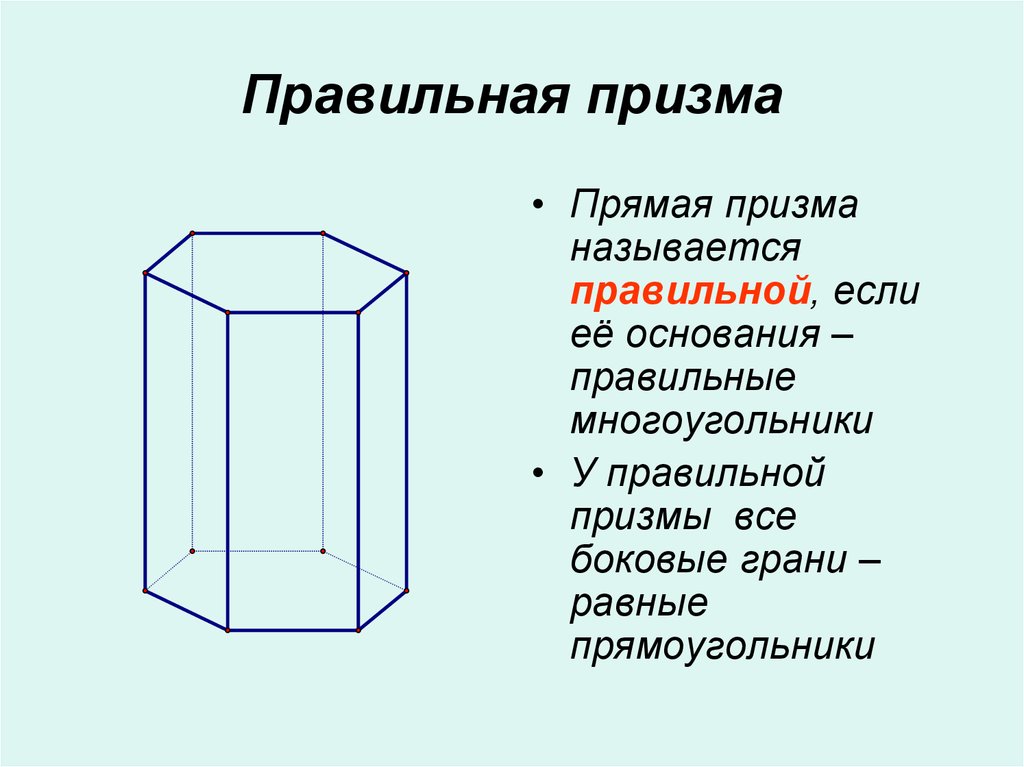
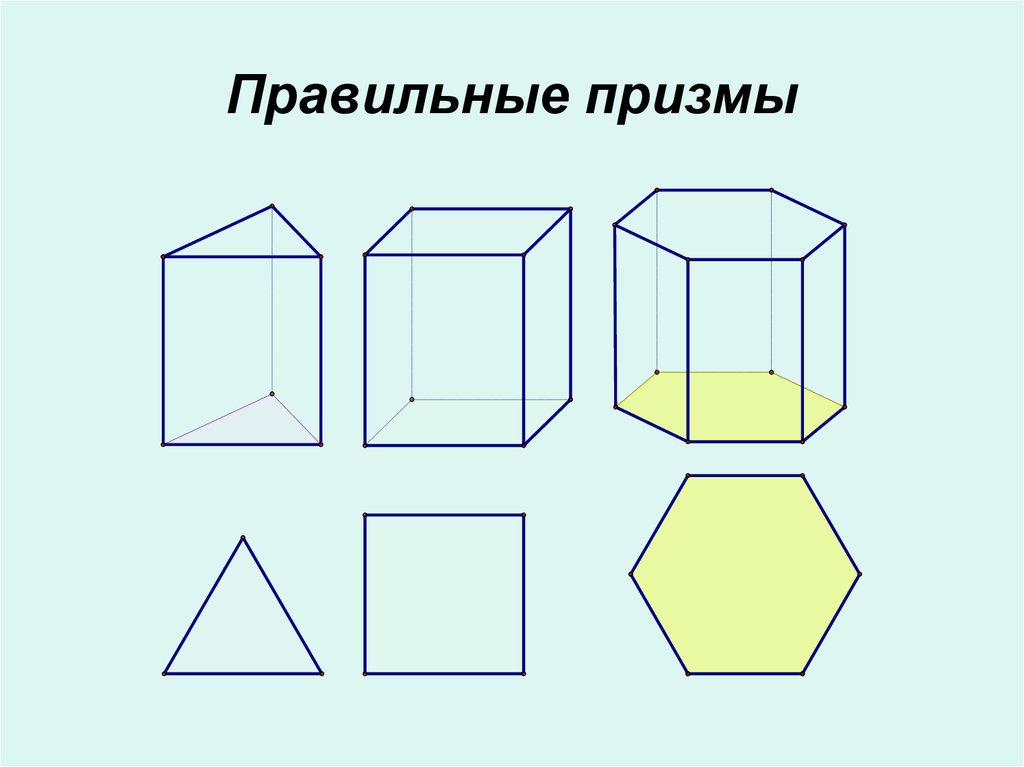
9. Правильная призма

• Прямая призма
называется
правильной, если
её основания –
правильные
многоугольники
• У правильной
призмы все
боковые грани –
равные
прямоугольники

10. Правильные призмы

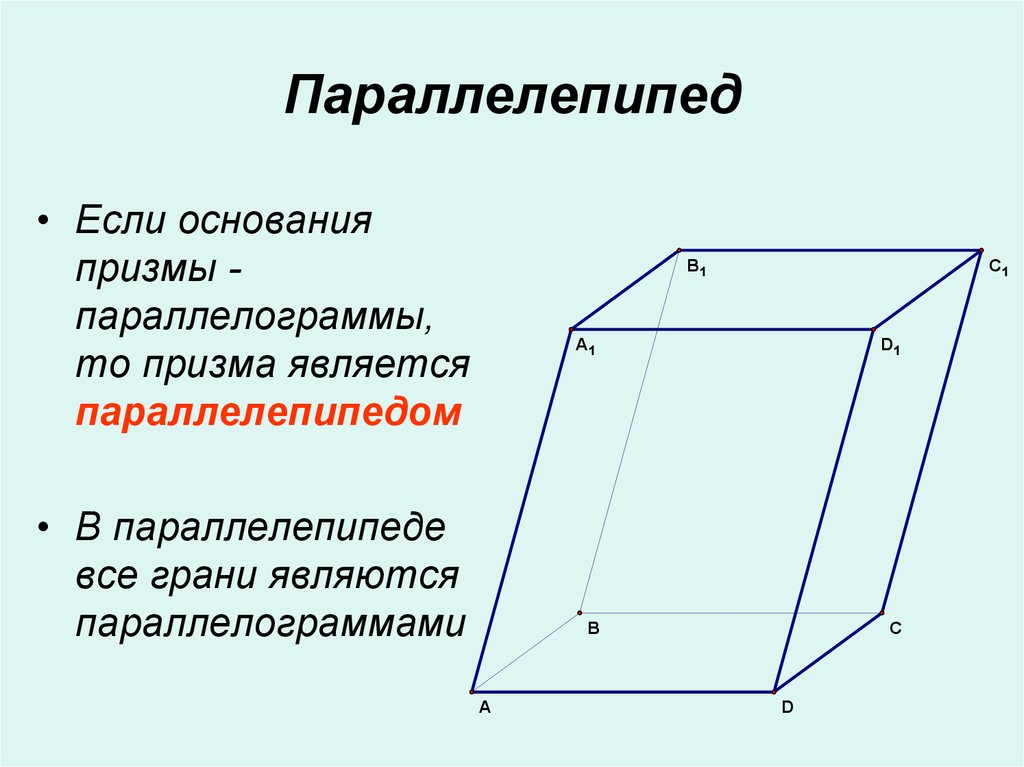
11. Параллелепипед

• Если основания
призмы параллелограммы,
то призма является
параллелепипедом
B1
• В параллелепипеде
все грани являются
параллелограммами
A
C1
A1
D1
B
C
D

12. Параллелепипед

Прямой параллелепипед
(боковое ребро перпендикулярно
основанию, боковые грани –
прямоугольники)
Наклонный параллелепипед
( боковое ребро не перпен
дикулярно основанию)
прямоугольный параллелепипед
(основание и все грани -прямоугольники)
правильный параллелепипед
(основание - квадрат)
куб
(все грани квадраты)

13. Свойства параллелепипеда

• 1. Середина диагонали параллелепипеда является центром
его симметрии.
• 2. Противолежащие грани попарно параллельны и равны.
• 3. Все диагонали параллелепипеда пересекаются в одной
точке и делятся ею пополам.
Свойства диагоналей прямоугольного
параллелепипеда.
• 1. Диагонали равны.
• 2. Квадрат длины диагонали параллелепипеда равен сумме
квадратов трех его измерений.

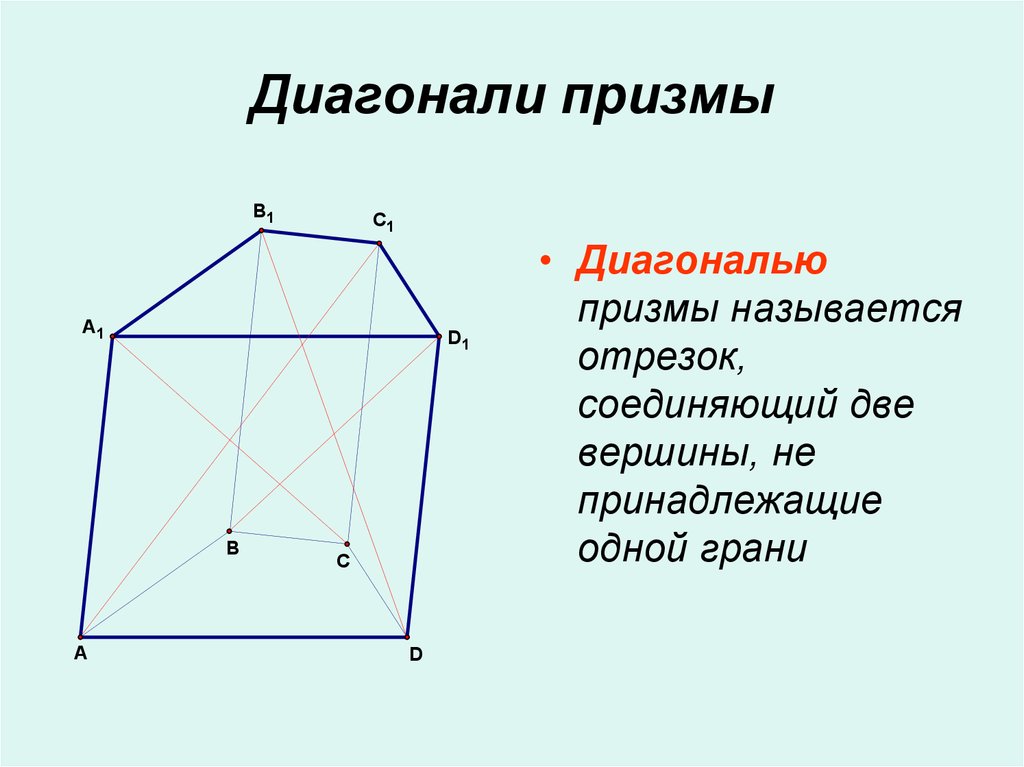
14. Диагонали призмы

B1
C1
A1
D1
B
A
C
D
• Диагональю
призмы называется
отрезок,
соединяющий две
вершины, не
принадлежащие
одной грани

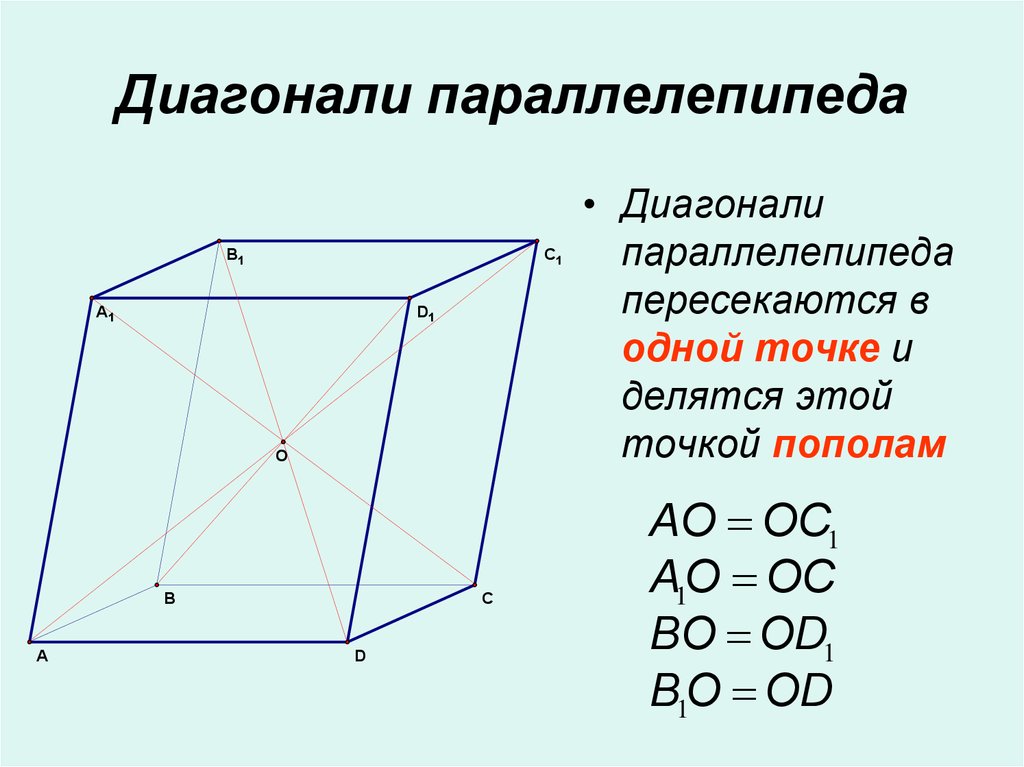
15. Диагонали параллелепипеда

B1
C1
A1
D1
O
B
A
C
D
• Диагонали
параллелепипеда
пересекаются в
одной точке и
делятся этой
точкой пополам
AO OC1
AO
OC
1
BO OD1
B1O OD

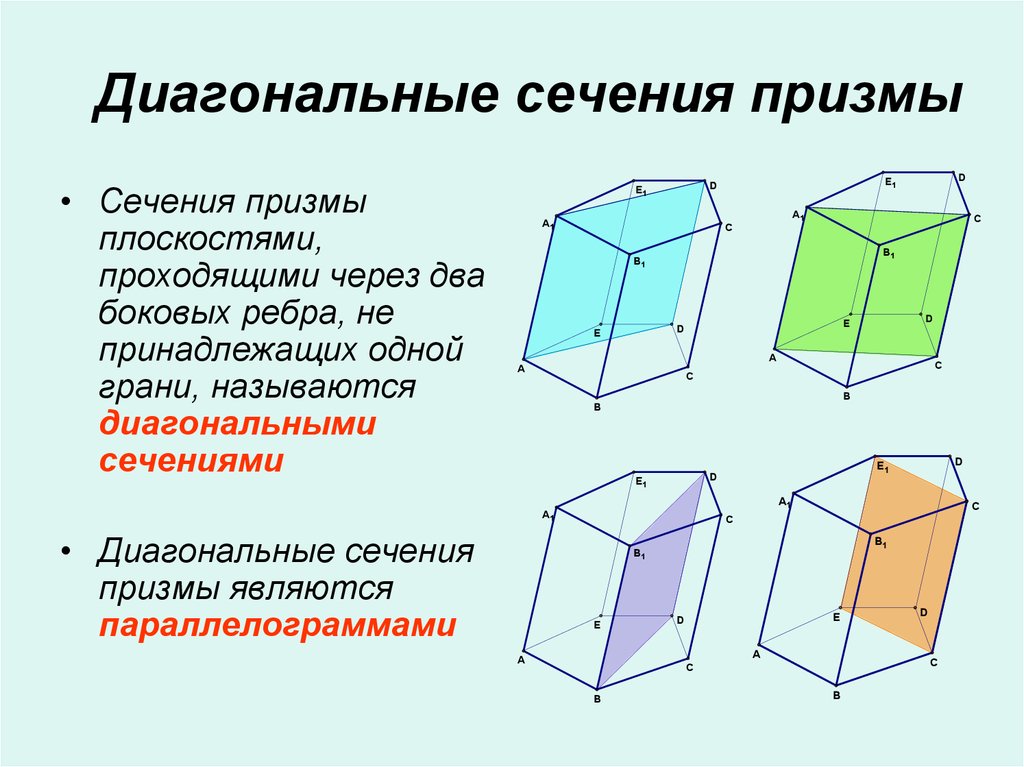
16. Диагональные сечения призмы

• Сечения призмы
плоскостями,
проходящими через два
боковых ребра, не
принадлежащих одной
грани, называются
диагональными
сечениями
D
E1
D
E1
A1
A1
C
C
B1
B1
D
E
D
E
A
A
C
C
B
B
E1
D
E1
D
A1
A1
• Диагональные сечения
призмы являются
параллелограммами
C
C
B1
B1
E
E
D
A
A
C
C
B
D
B

17. Диагональные сечения параллелепипеда

C1
B1
A
C1
B1
A1
D1
A1
D1
B
C
B
C
D
A
D

18. Площадь поверхности призмы

• Площадью полной поверхности
призмы называется сумма площадей
всех её граней Sполн
• Площадью боковой поверхности
призмы называется сумма площадей
её боковых граней Sбок
Sполн Sбок 2Sосн

19. Теорема о площади боковой поверхности прямой призмы

Теорема.
Площадь боковой поверхности прямой
призмы равна произведению периметра
основания на высоту призмы
Sбок Pосн H

20.

D1
C1
B1
A1
D
A
а
C
B
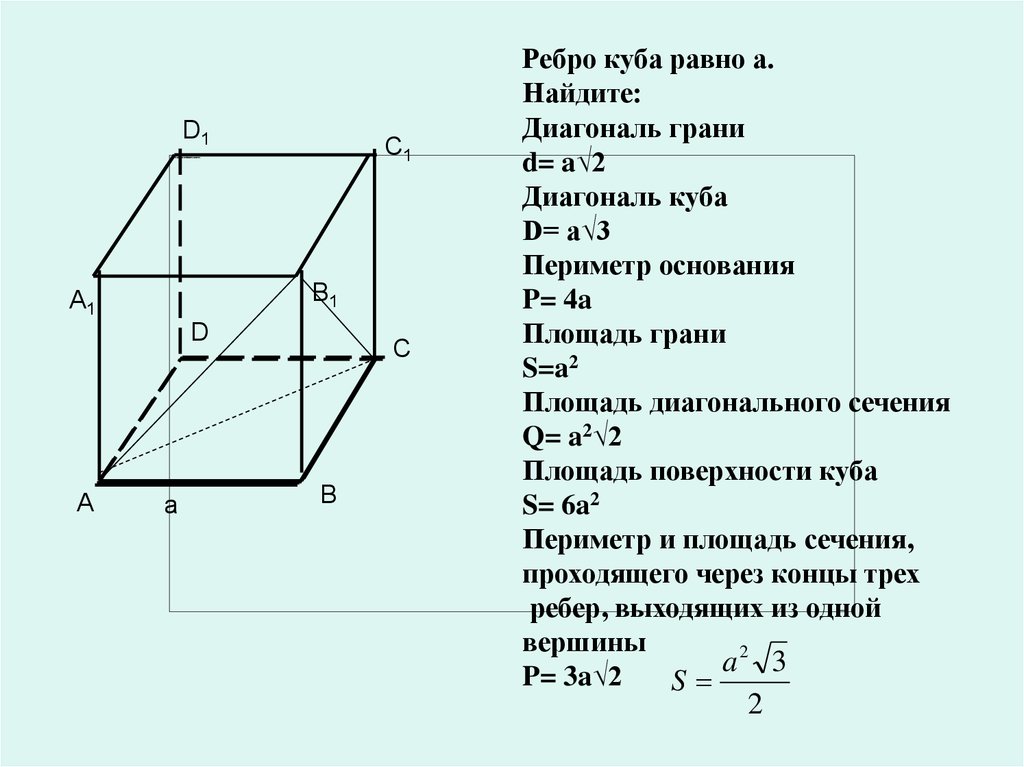
Ребро куба равно а.
Найдите:
Диагональ грани
d= a√2
Диагональ куба
D= a√3
Периметр основания
P= 4a
Площадь грани
S=a2
Площадь диагонального сечения
Q= a2√2
Площадь поверхности куба
S= 6a2
Периметр и площадь сечения,
проходящего через концы трех
ребер, выходящих из одной
вершины
2
a
3
P= 3a√2
S
2

21.

D1
C1
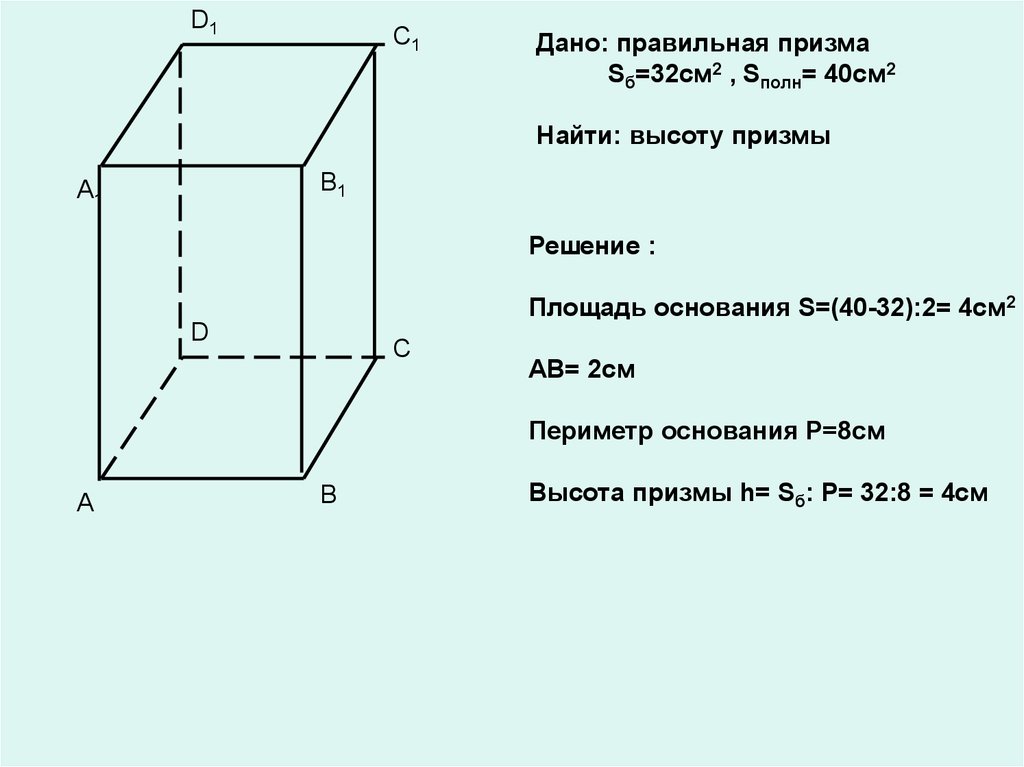
Дано: правильная призма
Sб=32см2 , Sполн= 40см2
Найти: высоту призмы
B1
A1
Решение :
Площадь основания S=(40-32):2= 4см2
D
C
АВ= 2см
Периметр основания Р=8см
A
B
Высота призмы h= Sб: Р= 32:8 = 4см

22.

C1
A1
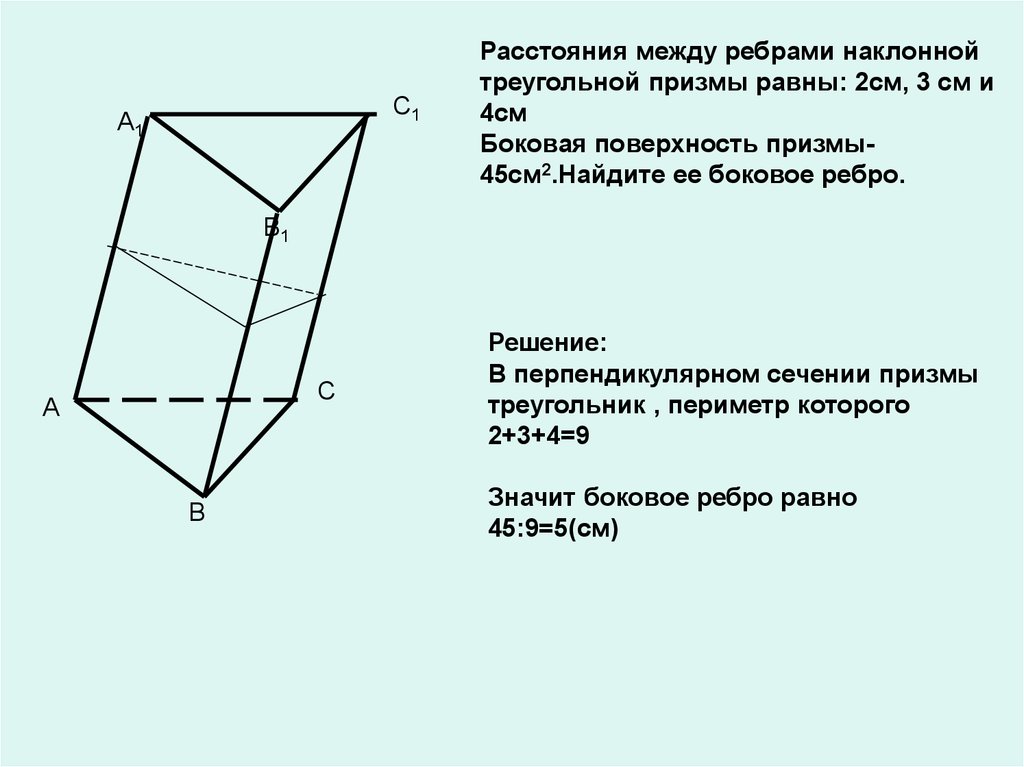
Расстояния между ребрами наклонной
треугольной призмы равны: 2см, 3 см и
4см
Боковая поверхность призмы45см2.Найдите ее боковое ребро.
B1
C
A
B
Решение:
В перпендикулярном сечении призмы
треугольник , периметр которого
2+3+4=9
Значит боковое ребро равно
45:9=5(см)

23. Справочный материал

формулы площади треугольника
1
1
1
S aha bhb chc
2
2
2
S p p a p b p c
где a, b, c – стороны треугольника
p – полупериметр

24. Справочный материал

формулы площади треугольника
1
S ab sin
2
S pr
abc
S
4R
где a, b, c – стороны треугольника
p – полупериметр
R – радиус описанной окружности
r – радиус вписанной окружности

25. Справочный материал

формулы площади параллелограмма
S aha
S ab sin
формулы площади других фигур
S ром ба aha
a b
S трапеции
h
2
S прям оуг ка ab
Sквадрата a
2

26. Призмы в окружающем мире