Призма. Боковые ребра

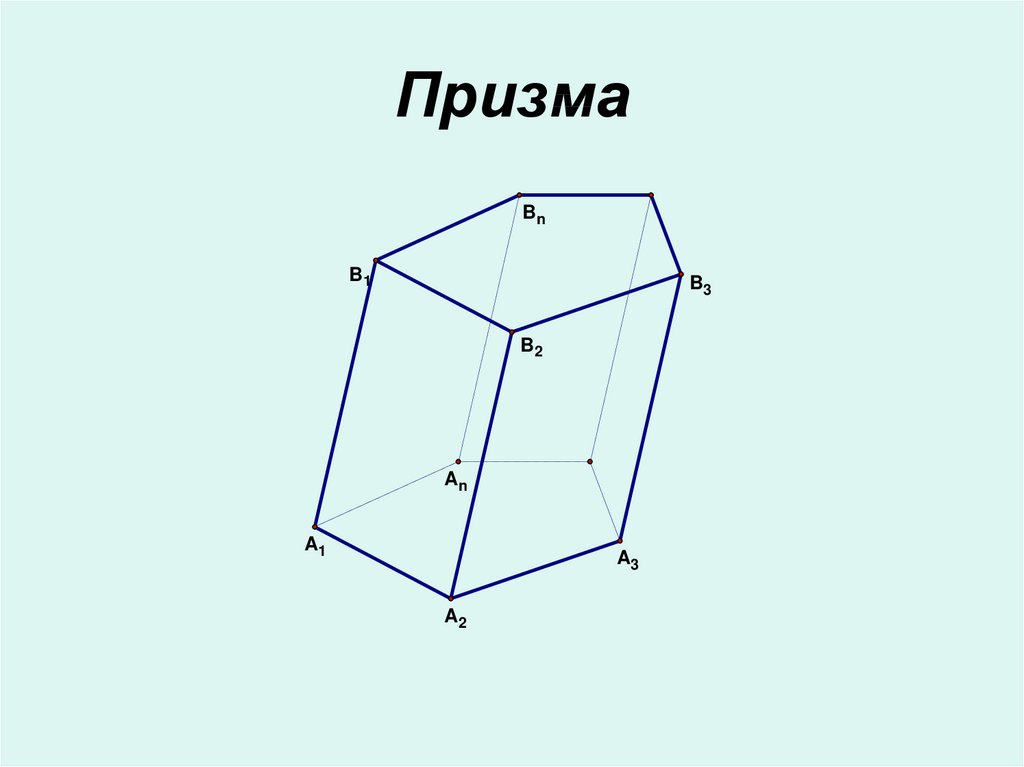
1. Призма

Bn
B1
B3
B2
An
A1
A3
A2

2.

• Отрезки A1B1,
A2B2, … , AnBn
называются
…………..призмы
Bn
B1
B3
B2
• Боковые ребра
призмы…………..
An
A1
A3
A2

3.

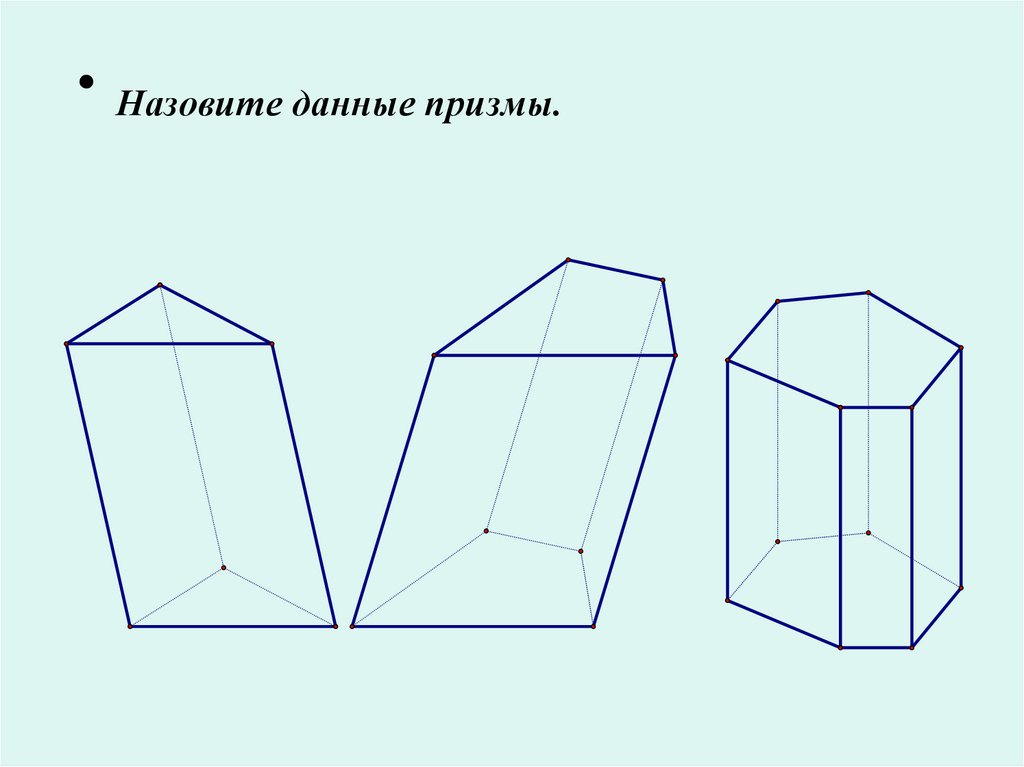
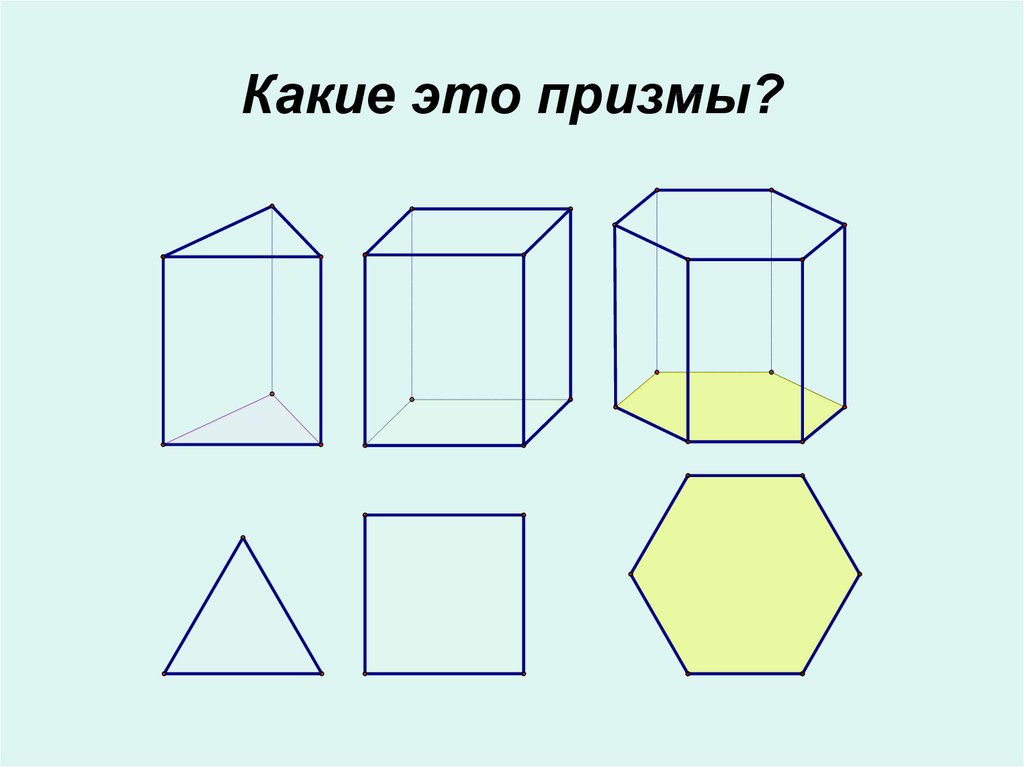
Назовите данные призмы.

4.

Bn
B1
B3
B2
An
A1
M
A3
A2
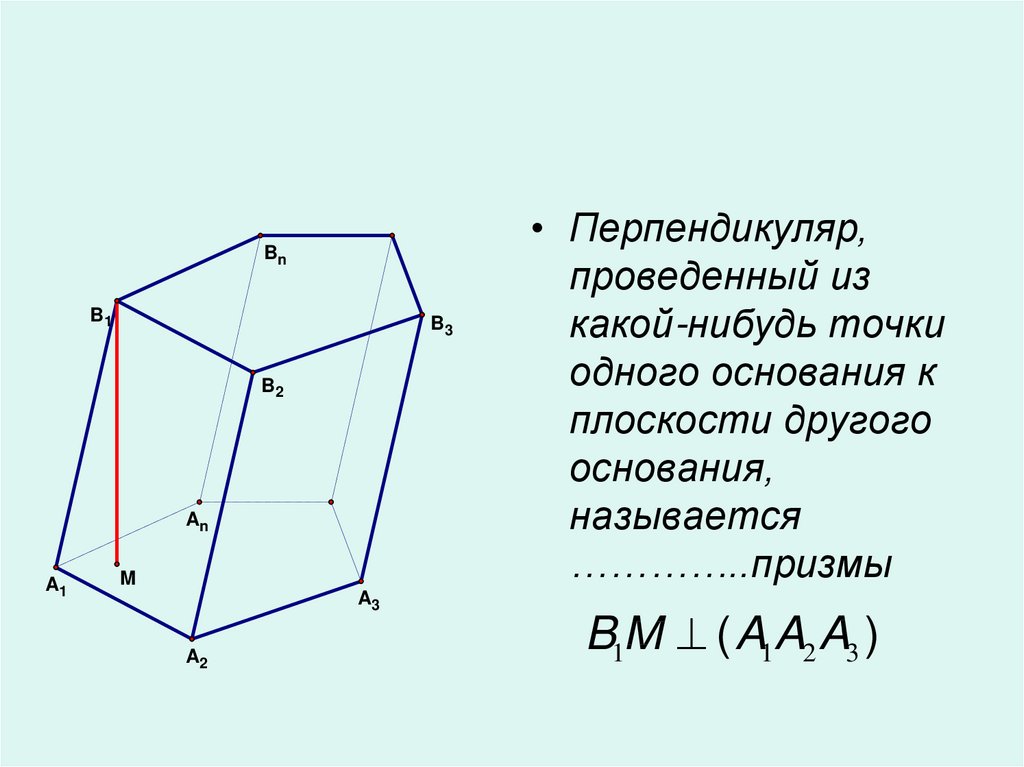
• Перпендикуляр,
проведенный из
какой-нибудь точки
одного основания к
плоскости другого
основания,
называется
…………..призмы
B1M ( A1A2 A3 )

5.

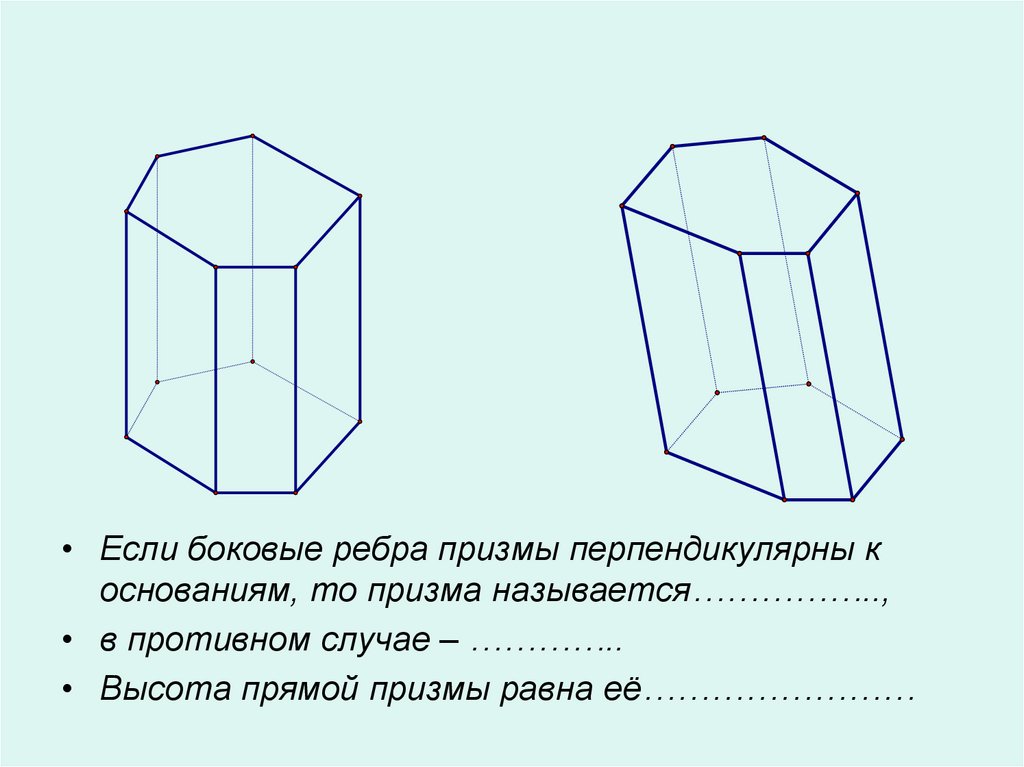
• Если боковые ребра призмы перпендикулярны к
основаниям, то призма называется……………..,
• в противном случае – …………..
• Высота прямой призмы равна её……………………

6.

• Прямая призма
называется……..,
если её основания –
правильные
многоугольники

7. Какие это призмы?

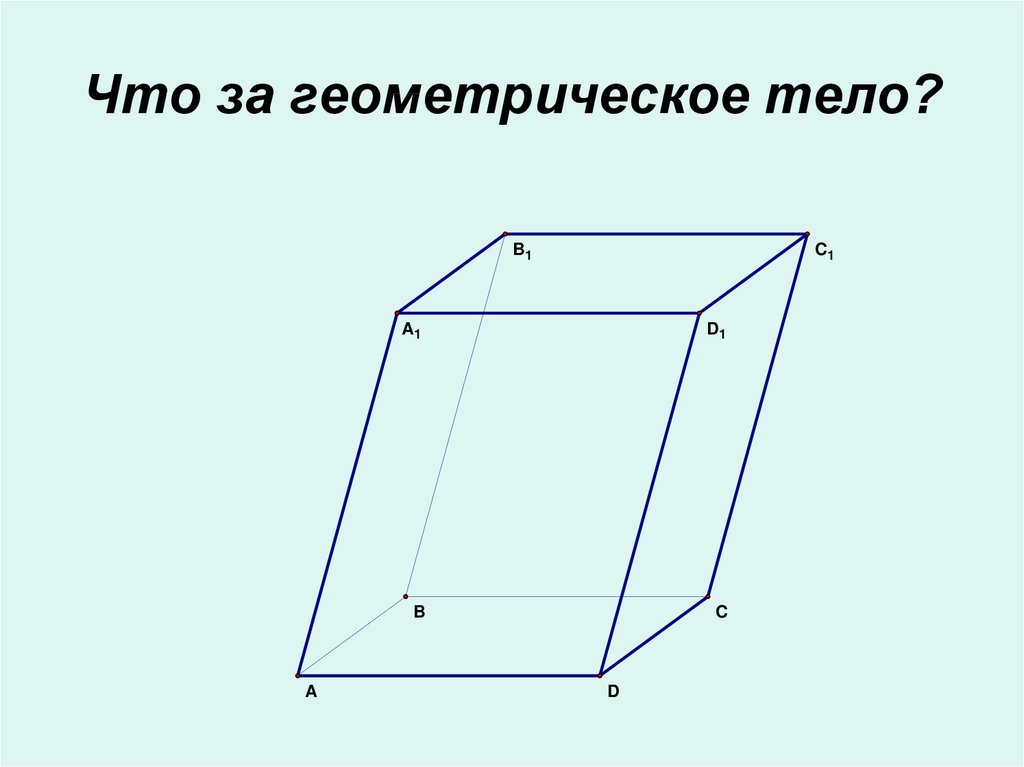
8. Что за геометрическое тело?

B1
A
C1
A1
D1
B
C
D

9. Диагонали призмы

B1
C1
A1
D1
B
A
C
D
• Диагональю
призмы называется
отрезок,
соединяющий две
вершины, не
принадлежащие
одной грани

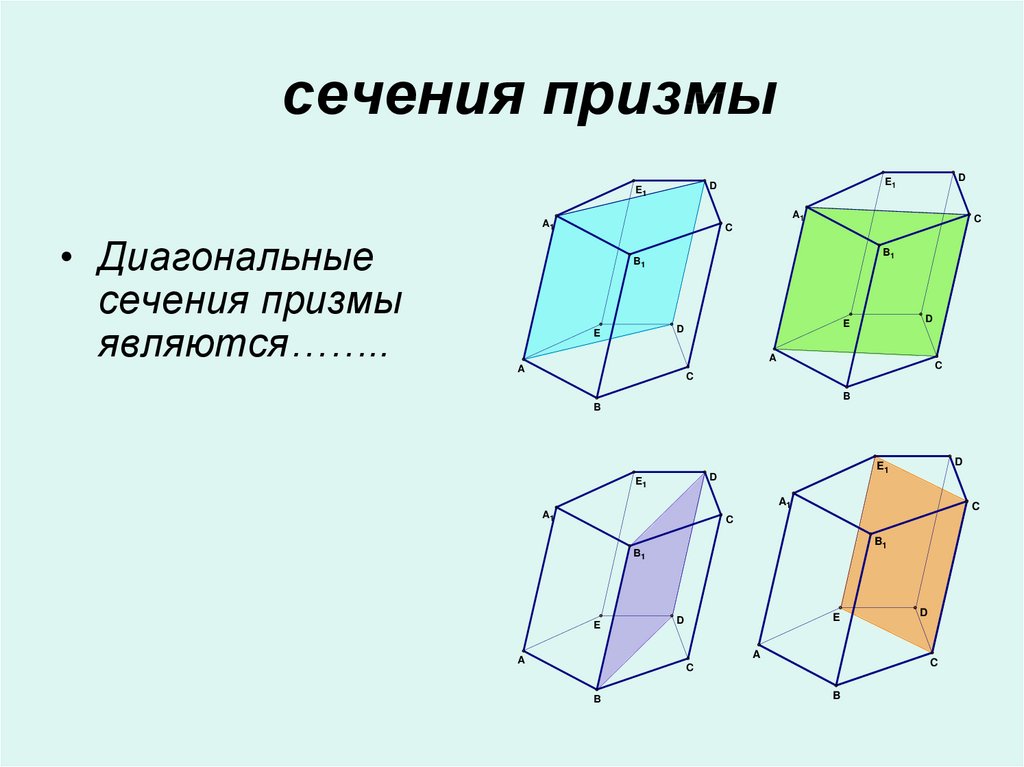
10. сечения призмы

A1
A1
• Диагональные
сечения призмы
являются……..
D
E1
D
E1
C
C
B1
B1
D
E
D
E
A
A
C
C
B
B
E1
D
E1
D
A1
A1
C
C
B1
B1
E
E
D
A
A
C
C
B
D
B

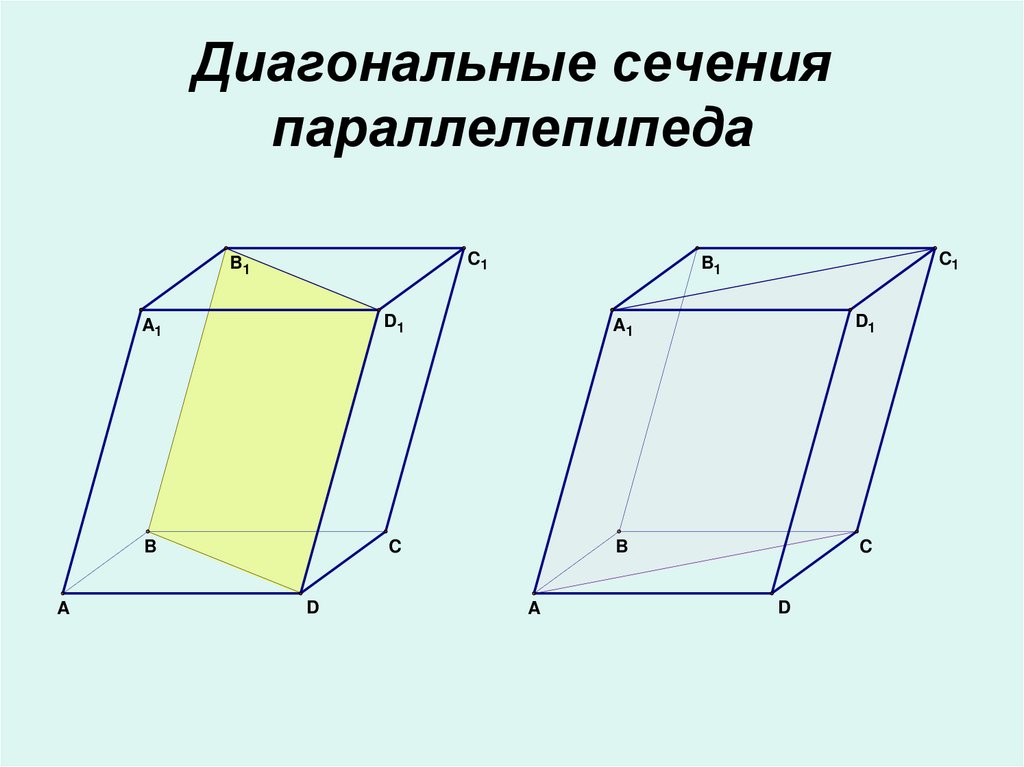
11. Диагональные сечения параллелепипеда

C1
B1
A
C1
B1
A1
D1
A1
D1
B
C
B
C
D
A
D

12. Площадь поверхности призмы

• Площадью полной поверхности
призмы называется сумма площадей
всех её граней Sполн
• Площадью боковой поверхности
призмы называется сумма площадей
её боковых граней Sбок
Sполн Sбок 2Sосн

13. Теорема о площади боковой поверхности прямой призмы

Теорема.
Площадь боковой поверхности прямой
призмы равна произведению периметра
основания на высоту призмы
Sбок Pосн H