Арксинус

1.

y
Повторим условие обратимой
функции.
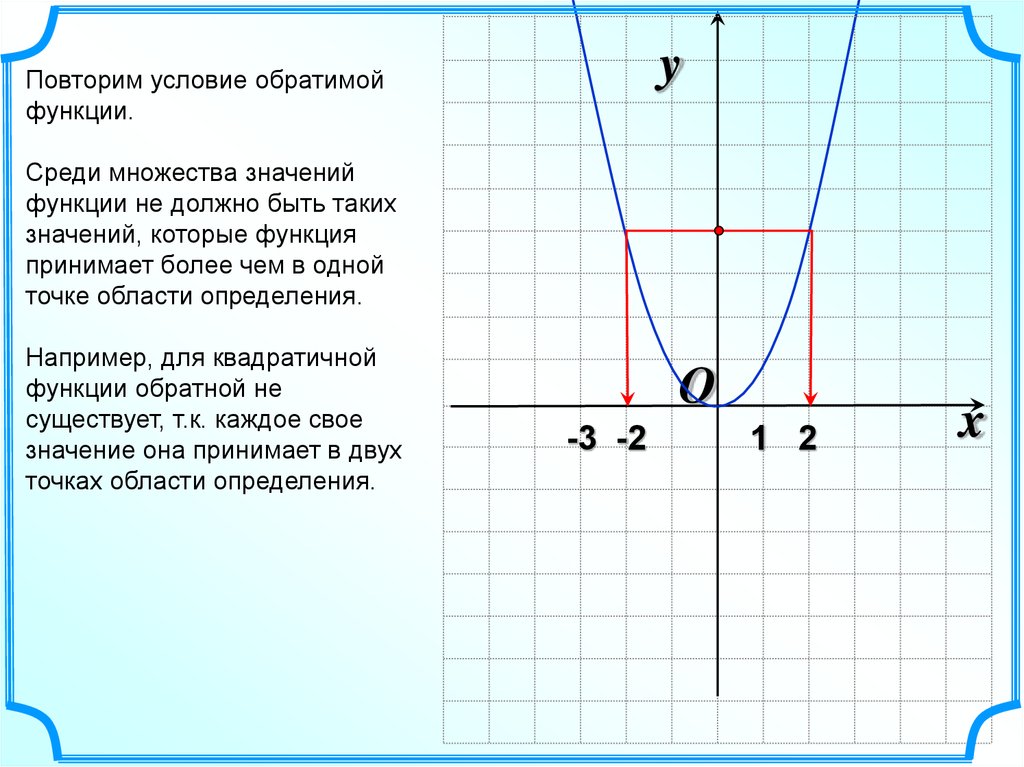
Среди множества значений
функции не должно быть таких
значений, которые функция
принимает более чем в одной
точке области определения.
Например, для квадратичной
функции обратной не
существует, т.к. каждое свое
значение она принимает в двух
точках области определения.
O
-3 -2
1 2
x

2.

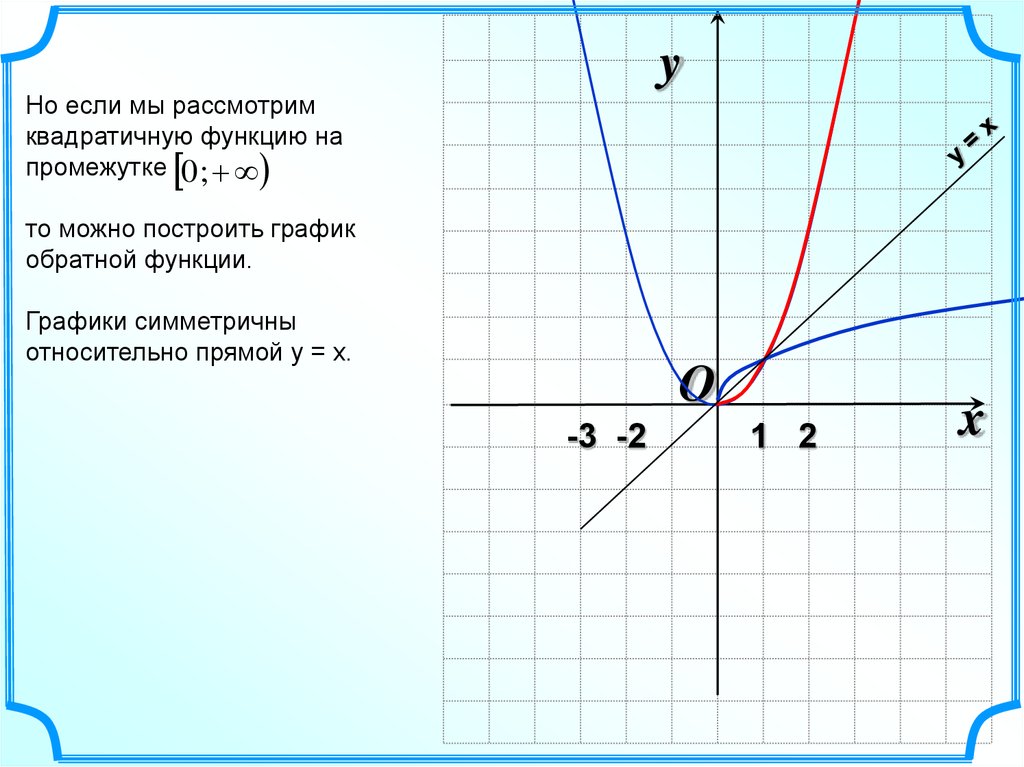
y
Но если мы рассмотрим
квадратичную функцию на
промежутке 0 ;
то можно построить график
обратной функции.
Графики симметричны
относительно прямой у = х.
O
-3 -2
1 2
x

3.

2
2
3
2
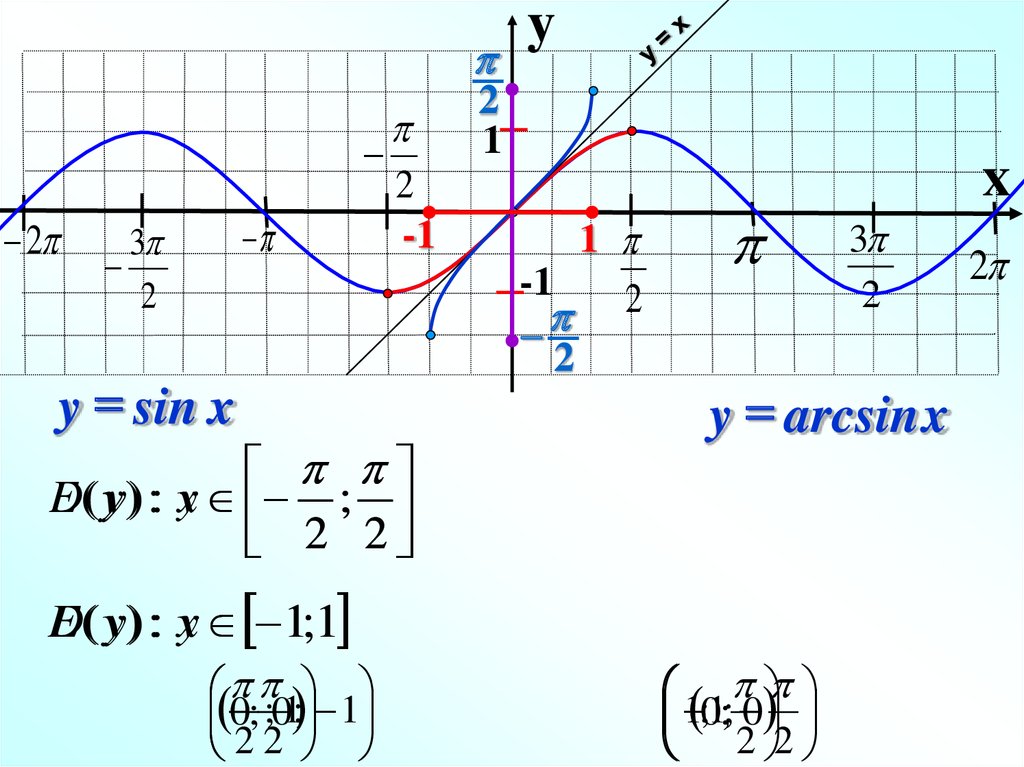
y = sin x
-1
D
E ( у ) : yх ;
2 2
y
2
1
1
-1
2
2
3
2
y = arcsin x
D
E( y) : yx 1;1
0; ;01; 1
22
x
1 ;01; 0
2 2
2

4.

5.

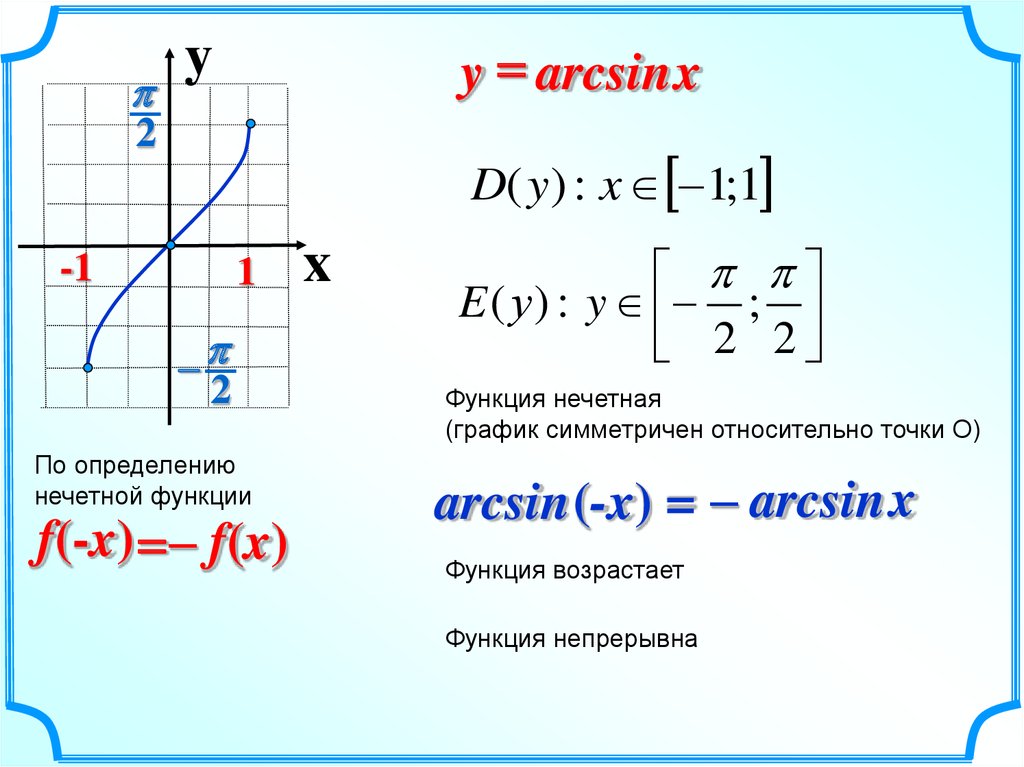
y = arcsin x
y
2
D( y) : x 1;1
-1
1
2
По определению
нечетной функции
f(-x) = – f(x)
x
E ( у ) : y ;
2 2
Функция нечетная
(график симметричен относительно точки О)
arcsin(-x) = – arcsinx
Функция возрастает
Функция непрерывна

6.

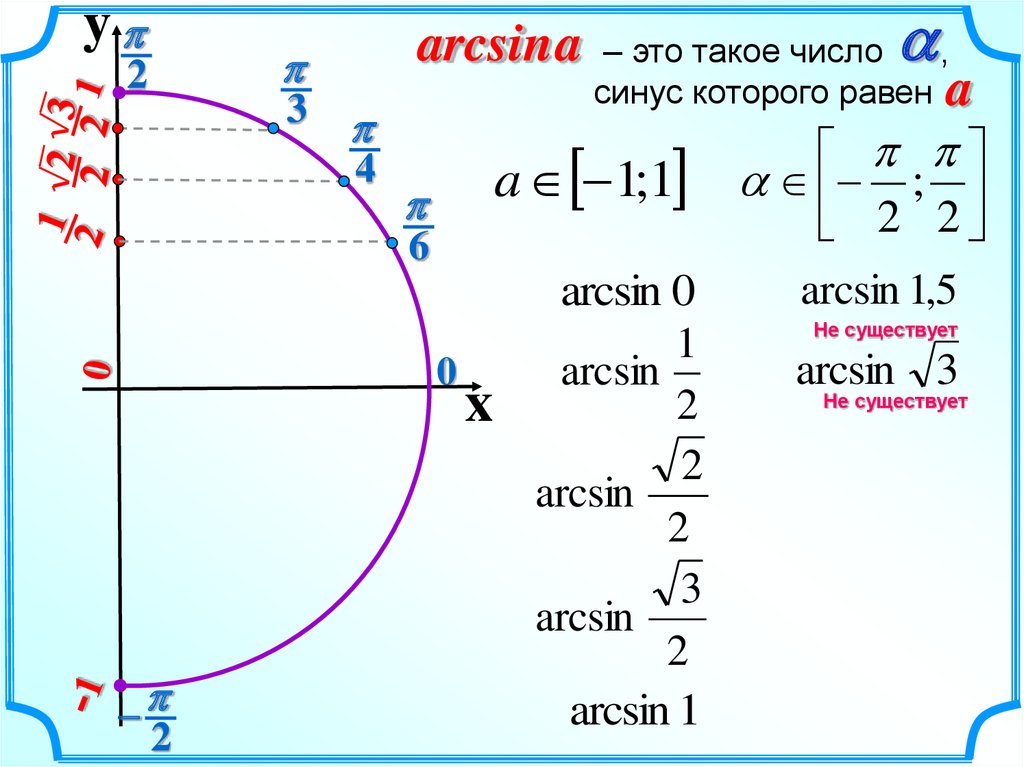
y
2
arcsina
3
4
a 1;1
6
0
2
x
a
– это такое число
,
синус которого равен a
arcsin 0
1
arcsin
2
2
arcsin
2
3
arcsin
2
arcsin 1
a ;
2 2
arcsin 1,5
Не существует
arcsin 3
Не существует

7.

arcsina
a
– это такое число
,
синус которого равен a
a 1;1
a ;
2 2
arcsin(-x) = – arcsinx
arcsin( 1)
1
arcsin( )
2
2
arcsin(
)
2
3
arcsin(
)
2
arcsin( 3 )
arcsin( 1,5)

8.

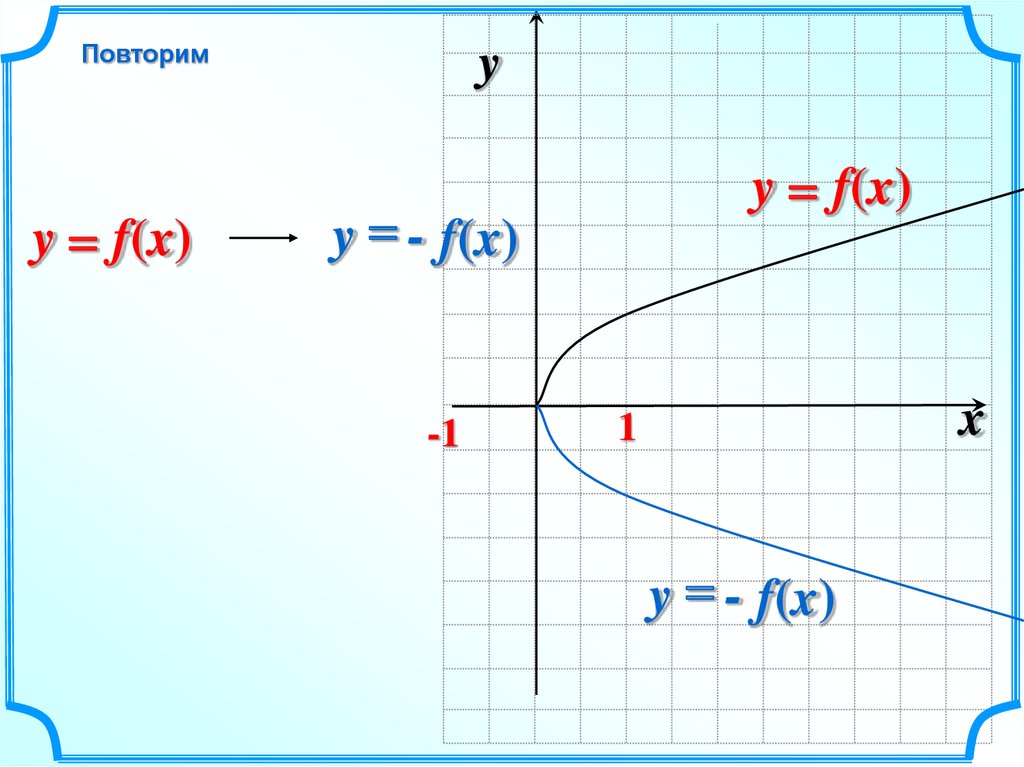
Повторим
y = f(x)
y
y = f(x)
y = - f(x)
-1
x
1
y = - f(x)

9.

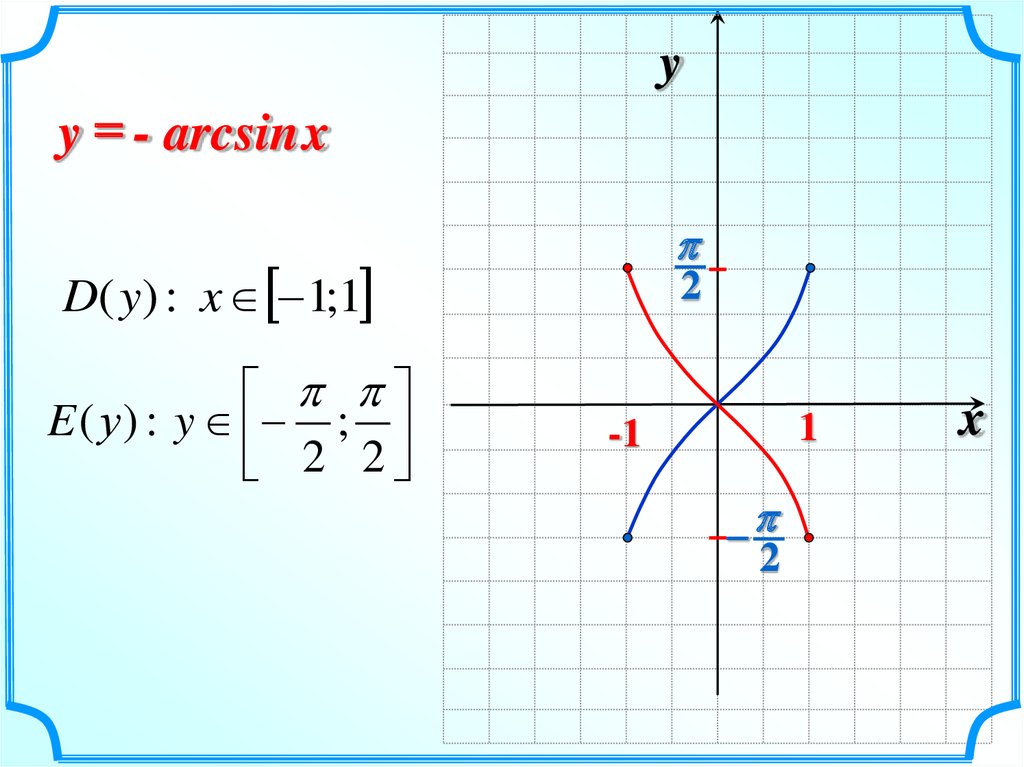
y
y = - arcsin x
D( y) : x 1;1
E ( у ) : y ;
2 2
2
1
-1
2
x

10.

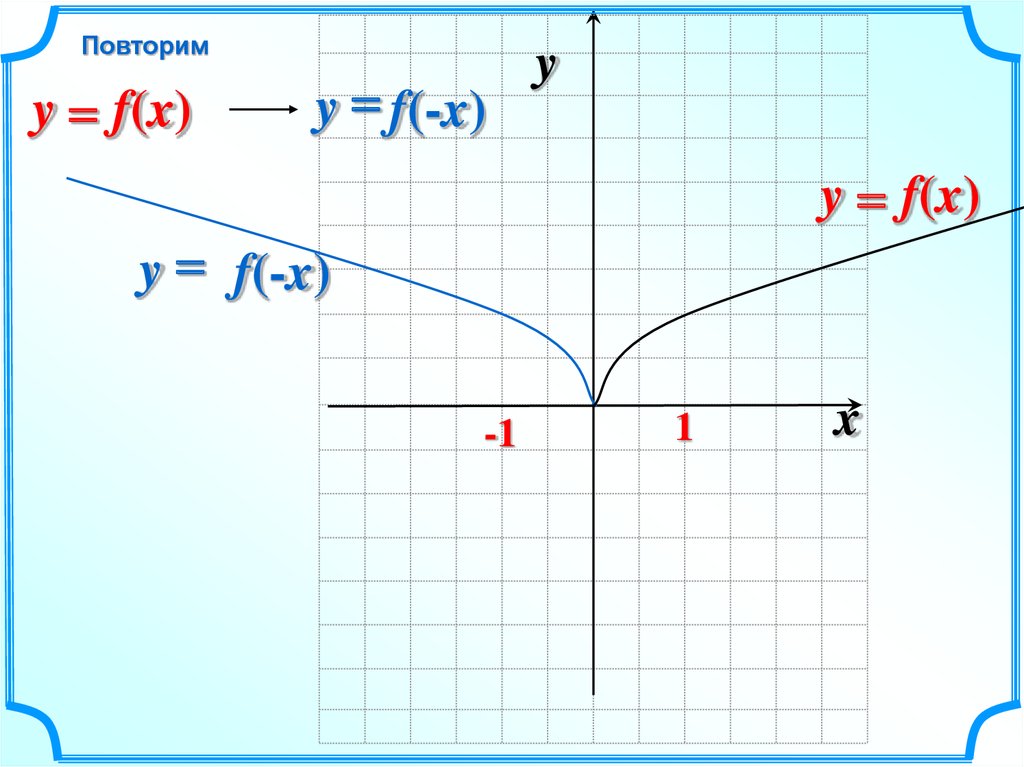
Повторим
y = f(x)
y = f(-x)
y
y = f(x)
y = f(-x)
-1
1
x

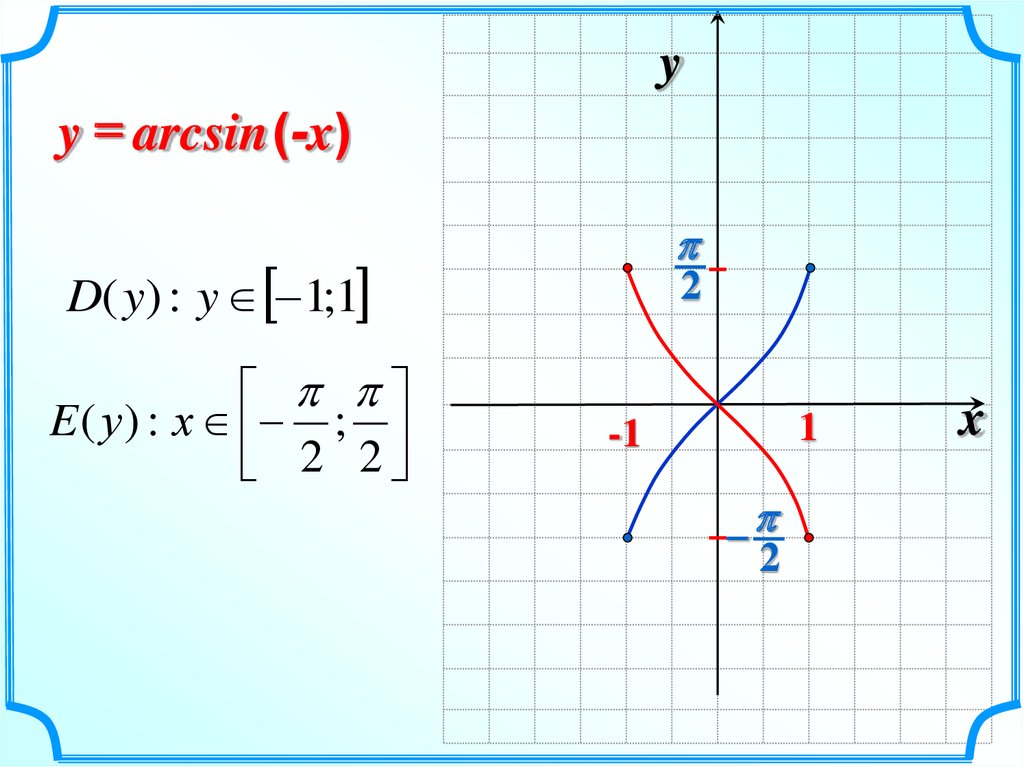
11.

y
y = arcsin (-x)
D( y) : y 1;1
E ( у ) : х ;
2 2
2
1
-1
2
x

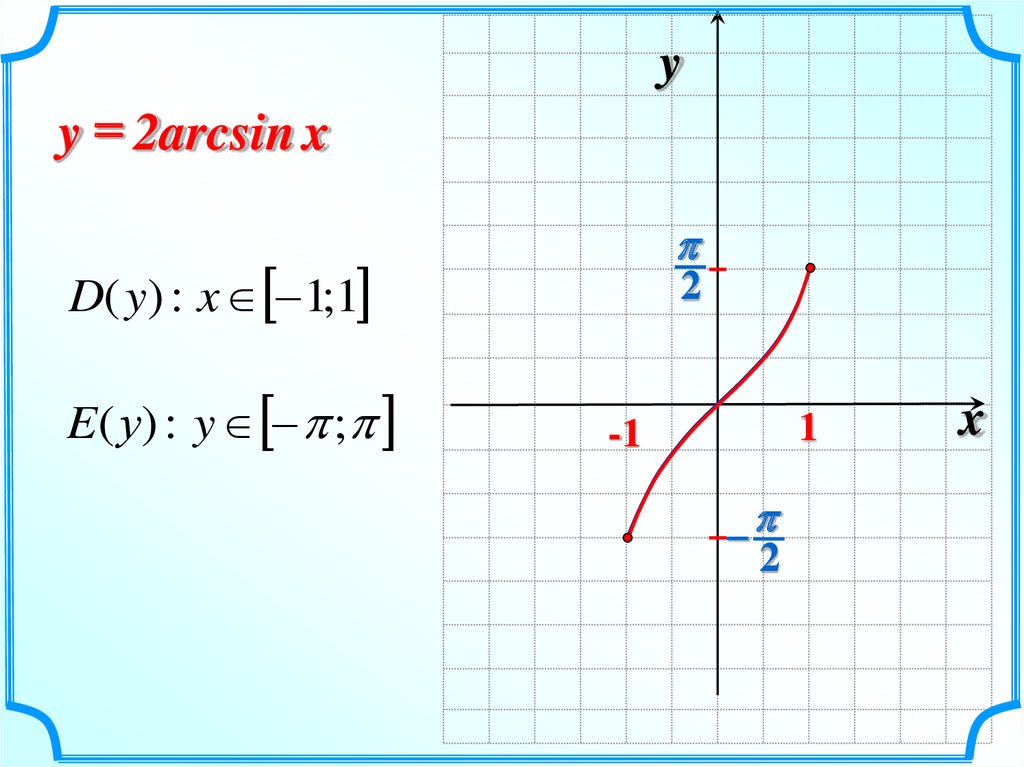
12.

y
y = 2arcsin x
D( y) : x 1;1
E( у) : y ;
2
1
-1
2
x

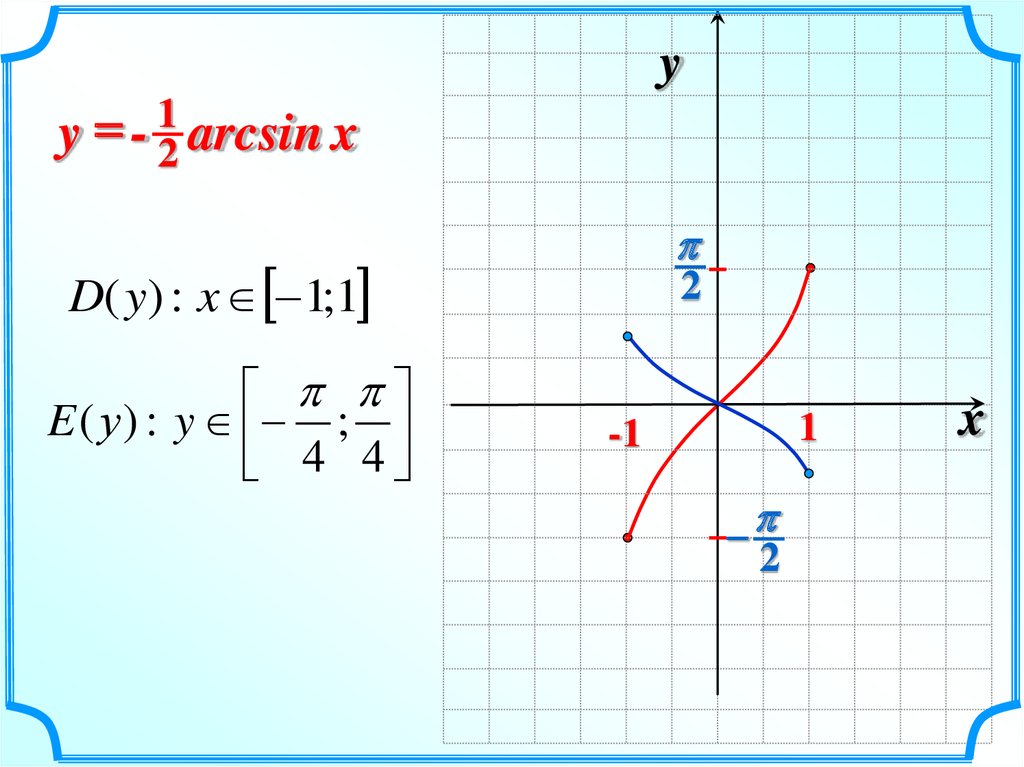
13.

y
1
=
y - 2 arcsin x
D( y) : x 1;1
E ( у ) : y ;
4 4
2
1
-1
2
x

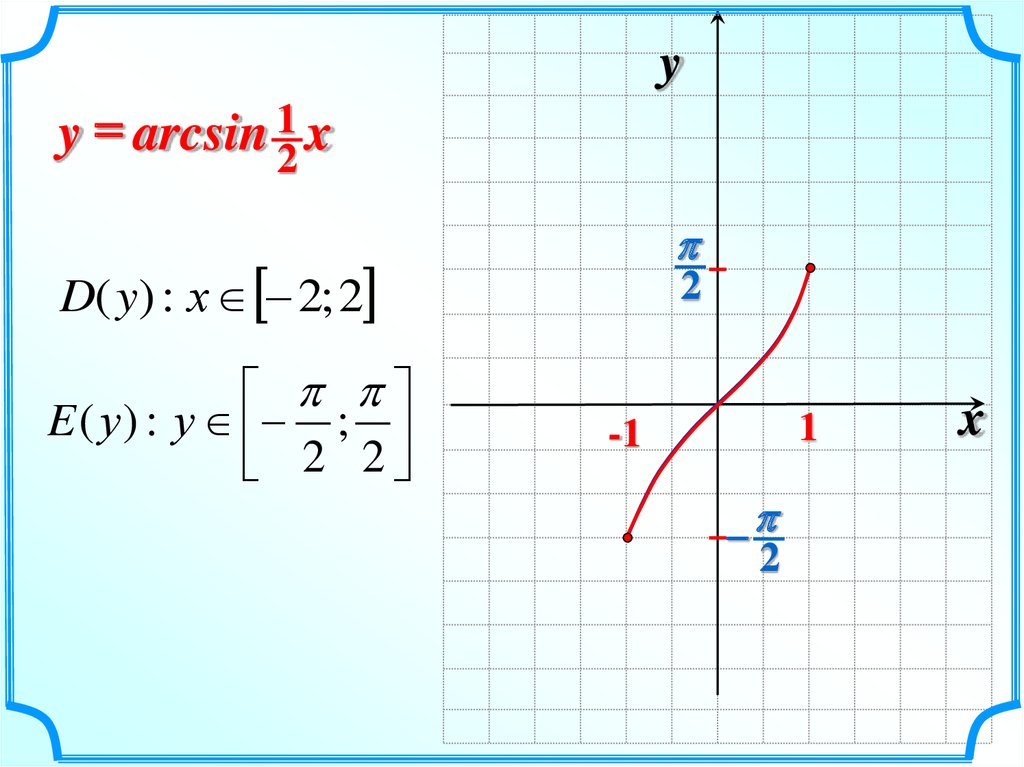
14.

y
y = arcsin 12 x
D( y) : х 2; 2
E ( у ) : у ;
2 2
2
1
-1
2
x

15.

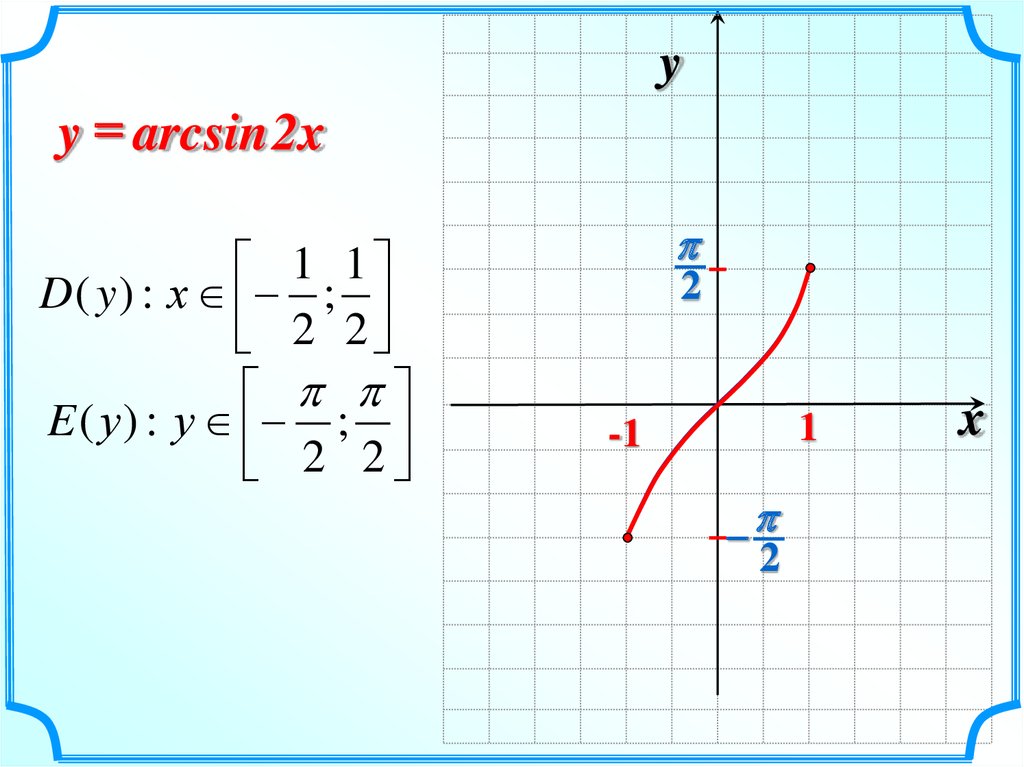
y
y = arcsin 2x
1 1
D ( y ) : х ;
2 2
E ( у ) : у ;
2 2
2
1
-1
2
x

16.

y
2
=
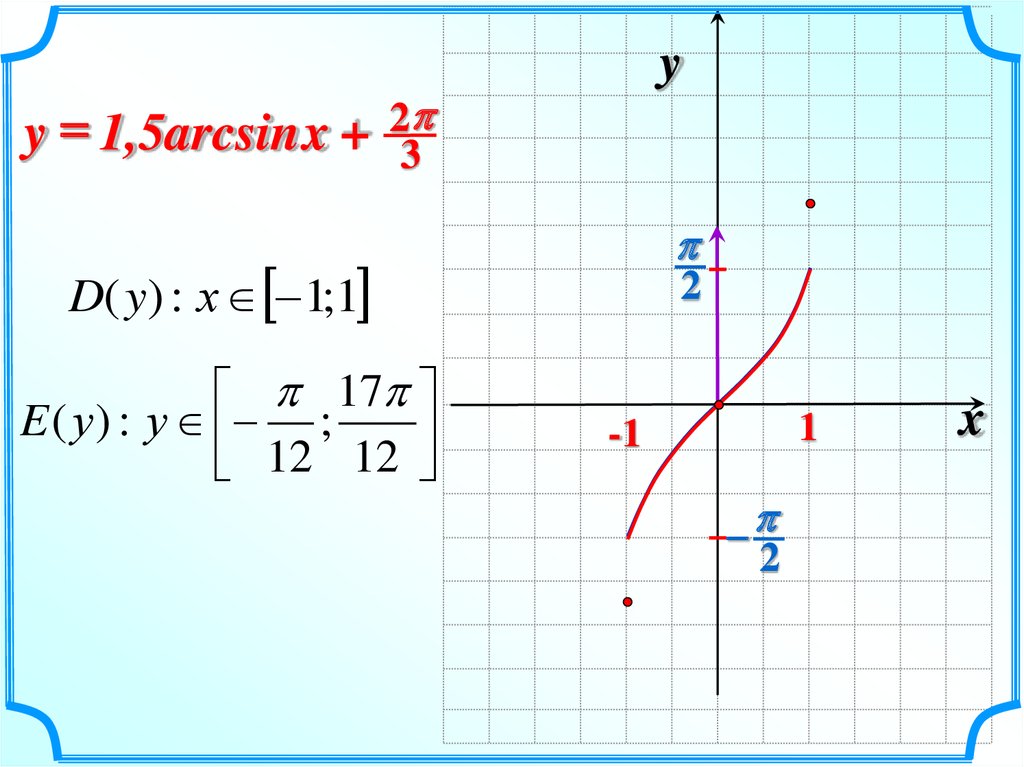
y 1,5arcsin x + 3
D( y) : х 1;1
17
E ( у ) : у ;
12
12
2
1
-1
2
x

17.

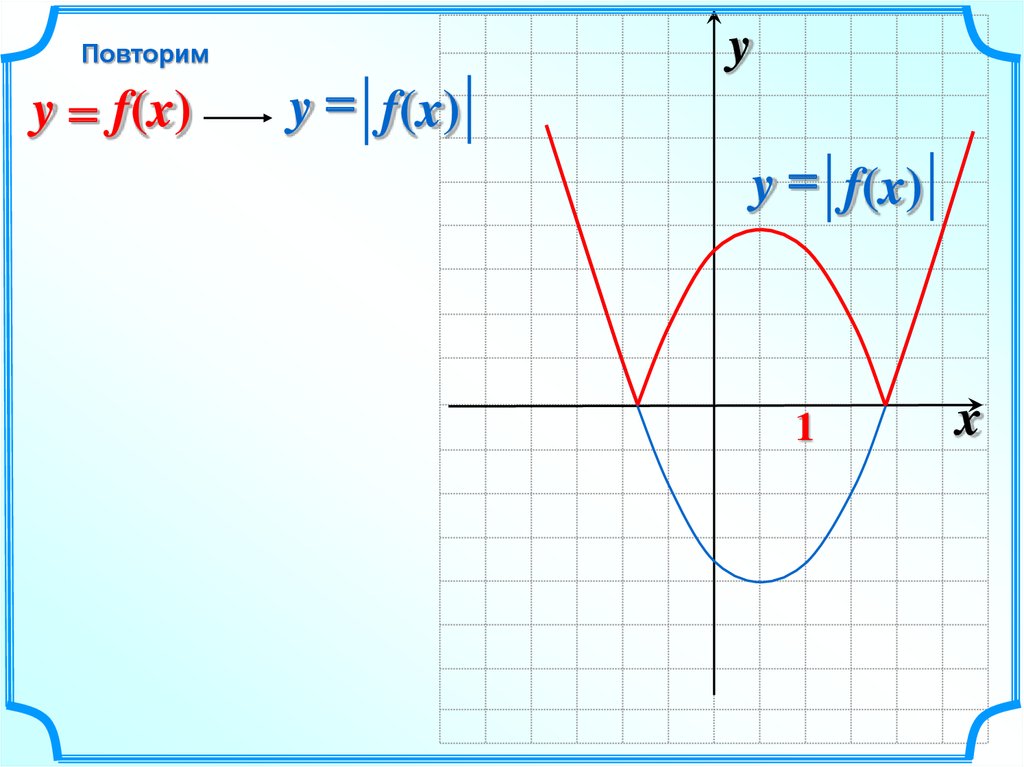
Повторим
y = f(x)
y = f(x)
y
y = f(x)
1
x

18.

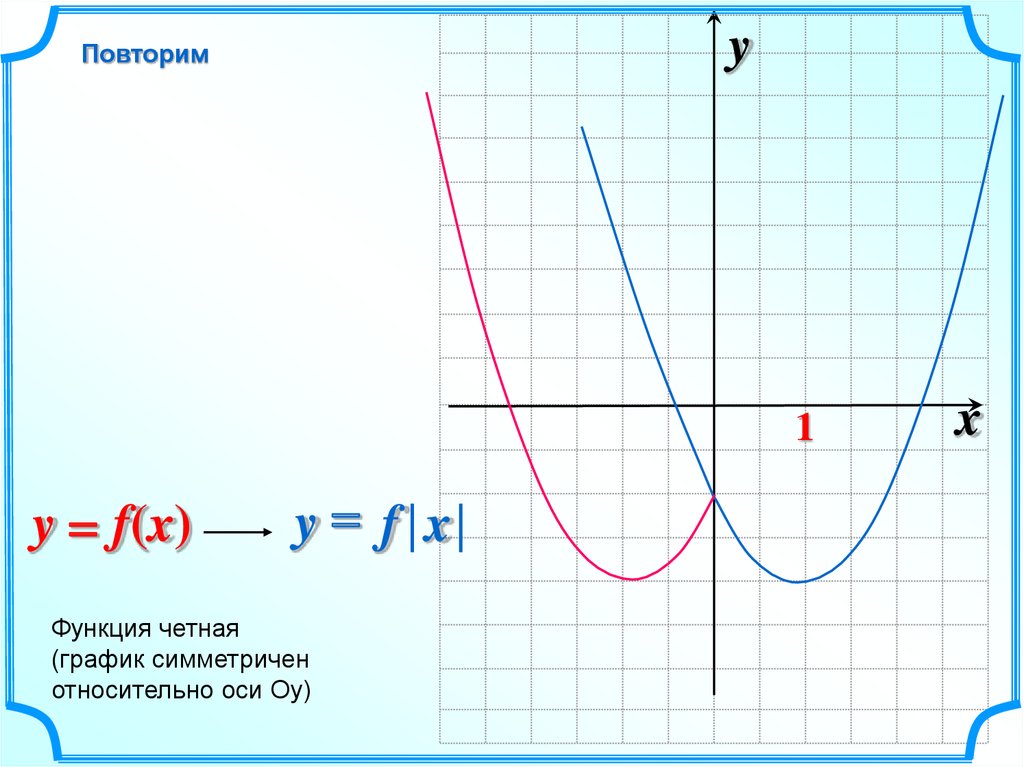
y
Повторим
1
y = f(x)
y= f x
Функция четная
(график симметричен
относительно оси Оу)
x

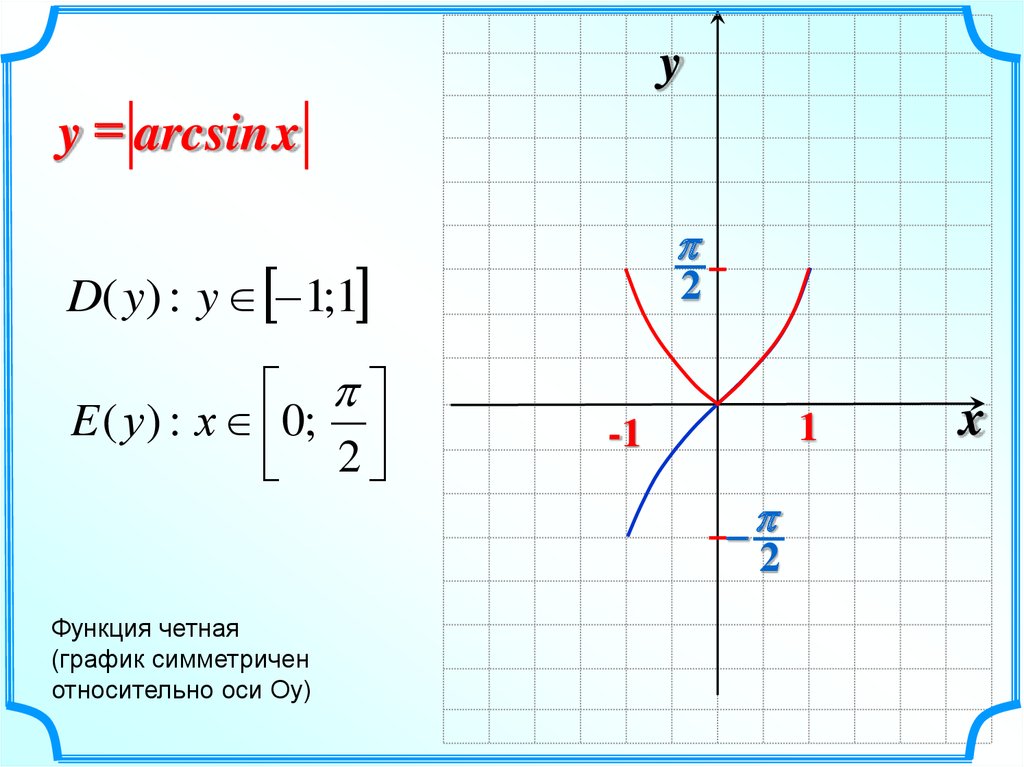
19.

y
y = arcsin x
D( y) : y 1;1
E ( у ) : х 0;
2
Функция четная
(график симметричен
относительно оси Оу)
2
1
-1
2
x

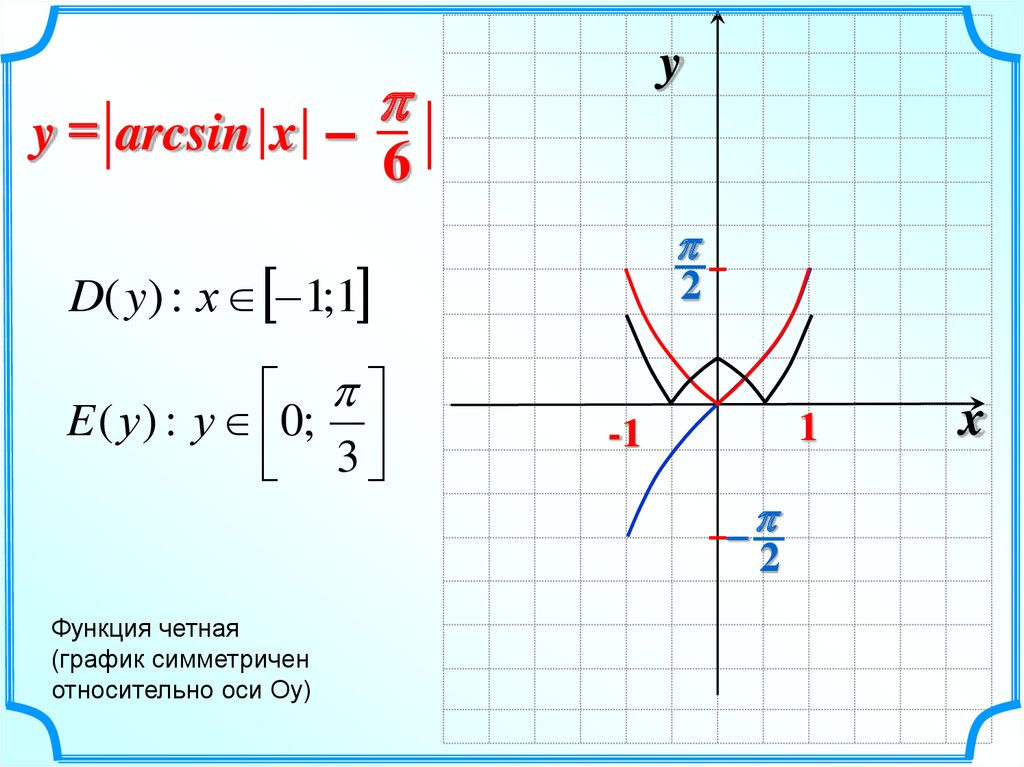
20.

y
y = arcsin x –
6
D( y) : х 1;1
E ( у ) : у 0;
3
Функция четная
(график симметричен
относительно оси Оу)
2
1
-1
2
x

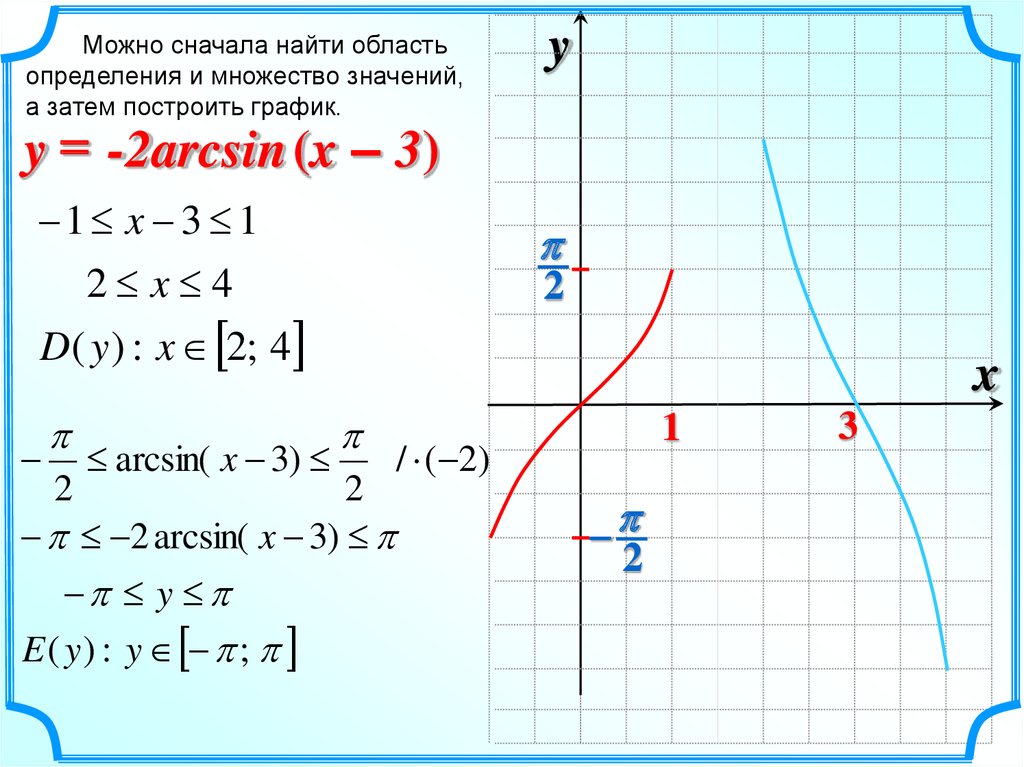
21.

Можно сначала найти область
определения и множество значений,
а затем построить график.
y
y = -2arcsin (x – 3)
1 x 3 1
2 x 4
2
D ( y ) : x 2; 4
2
arcsin( x 3)
x
2
2 arcsin( x 3)
y
E ( y ) : y ;
1
/ ( 2)
2
3

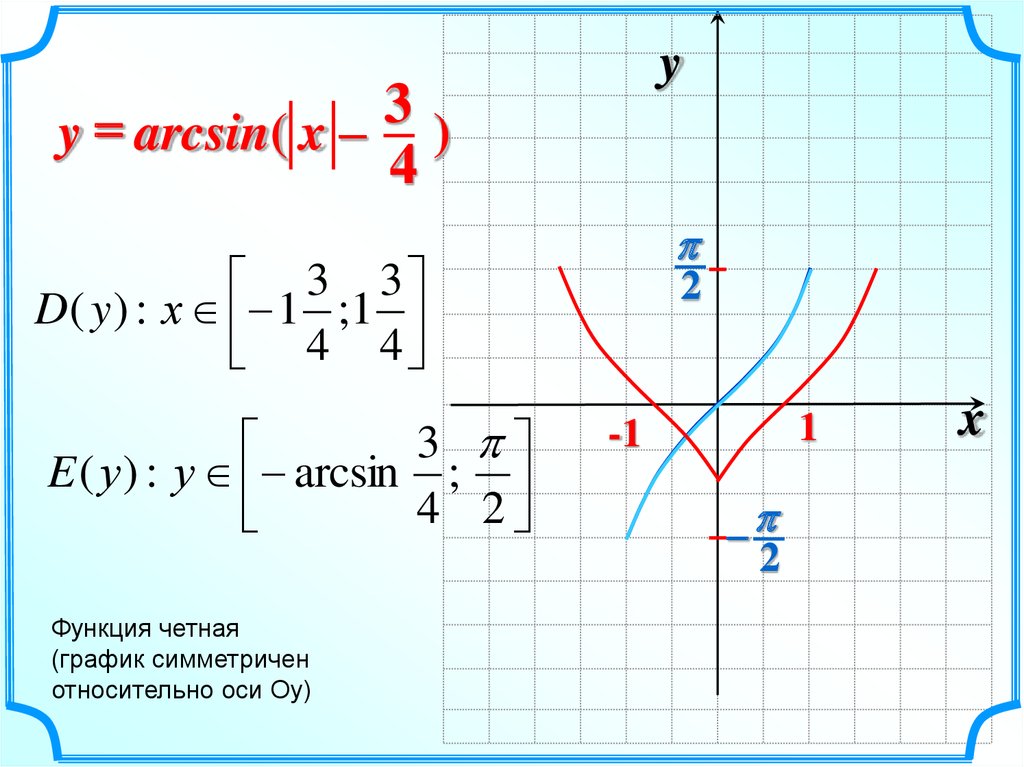
22.

y
3
y = arcsin( x – )
4
3 3
D ( y ) : х 1 ;1
4 4
3
E ( у ) : у arcsin ;
4 2
Функция четная
(график симметричен
относительно оси Оу)
2
1
-1
2
x