Similar presentations:
Поверхности. Лекция 4
1.
Лекция 4ПОВЕРХНОСТИ
Красовская Н.И.
2.
Поверхность– это совокупность всех
последовательных положений
некоторой перемещающейся в
пространстве линии
Красовская Н.И.
3.
Способы образования и заданияповерхностей.
Каркас поверхности.
Определитель поверхности
Красовская Н.И.
4.
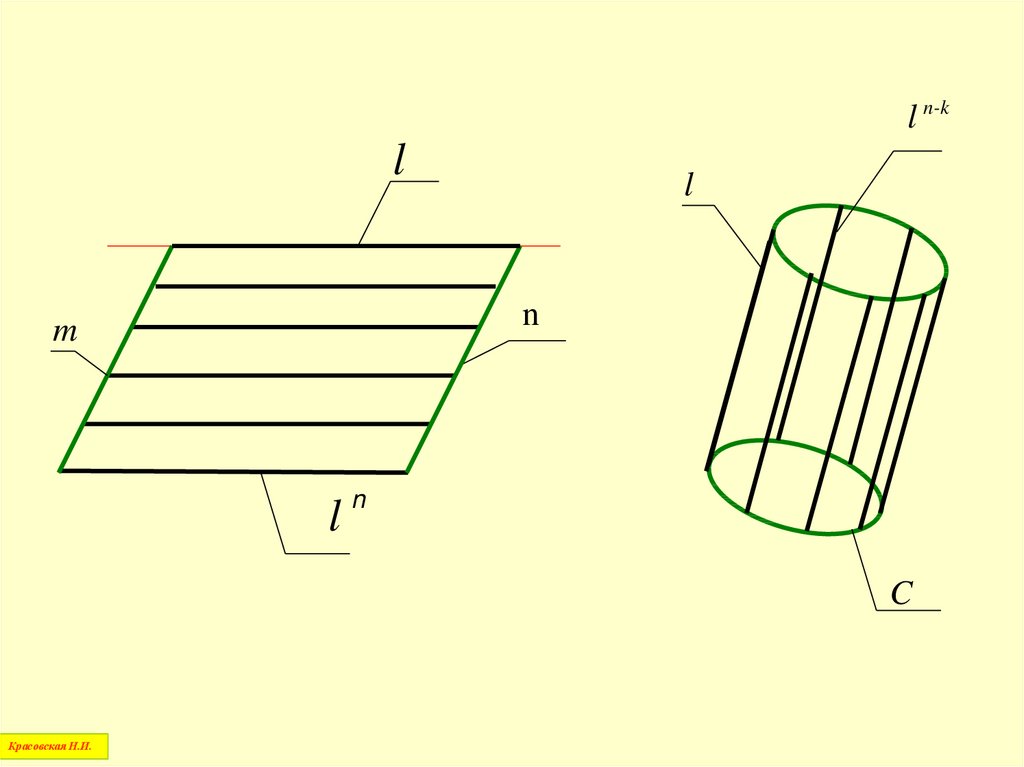
Движущаяся в процессе образованияповерхности линия называется
образующей
Линия, по которой скользит образующая,
называется направляющей
Красовская Н.И.
5.
l n-kl
l
n
m
l
n
C
Красовская Н.И.
6.
Совокупность намеченных на поверхностиобразующих и направляющих линий
называется линейным каркасом
поверхности
Красовская Н.И.
7.
ΣΦ
l
l
n
Красовская Н.И.
m
8.
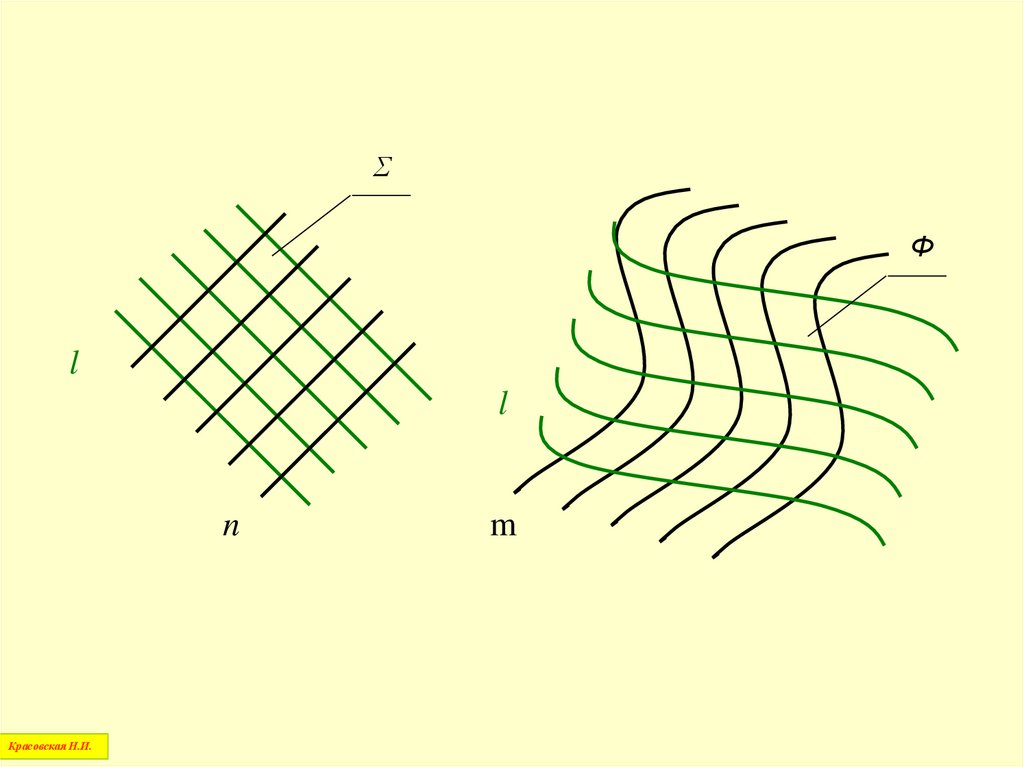
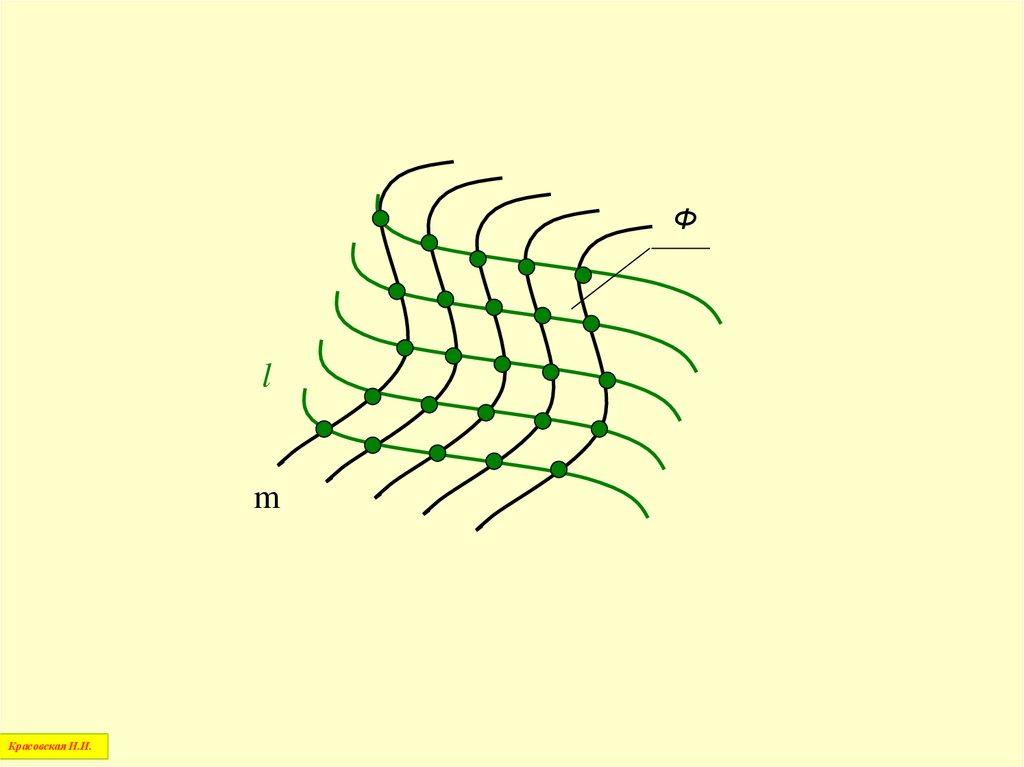
Совокупность точек на поверхности,выбранных таким образом, чтобы,
ориентируясь по ним, можно достаточно
полно представить форму поверхности,
называется точечным каркасом
поверхности
Красовская Н.И.
9.
Φl
m
Красовская Н.И.
10.
il
i
l
c
Красовская Н.И.
11.
Совокупность независимых условий,однозначно задающих поверхность,
называется её
определителем
Ф(l,i)[A]
Красовская Н.И.
12.
а)б)
l
S
S∞
l
m
Ф(l,m)[A]
Красовская Н.И.
m
Ф(l,m)[A]
13.
Очерк поверхностиКрасовская Н.И.
14.
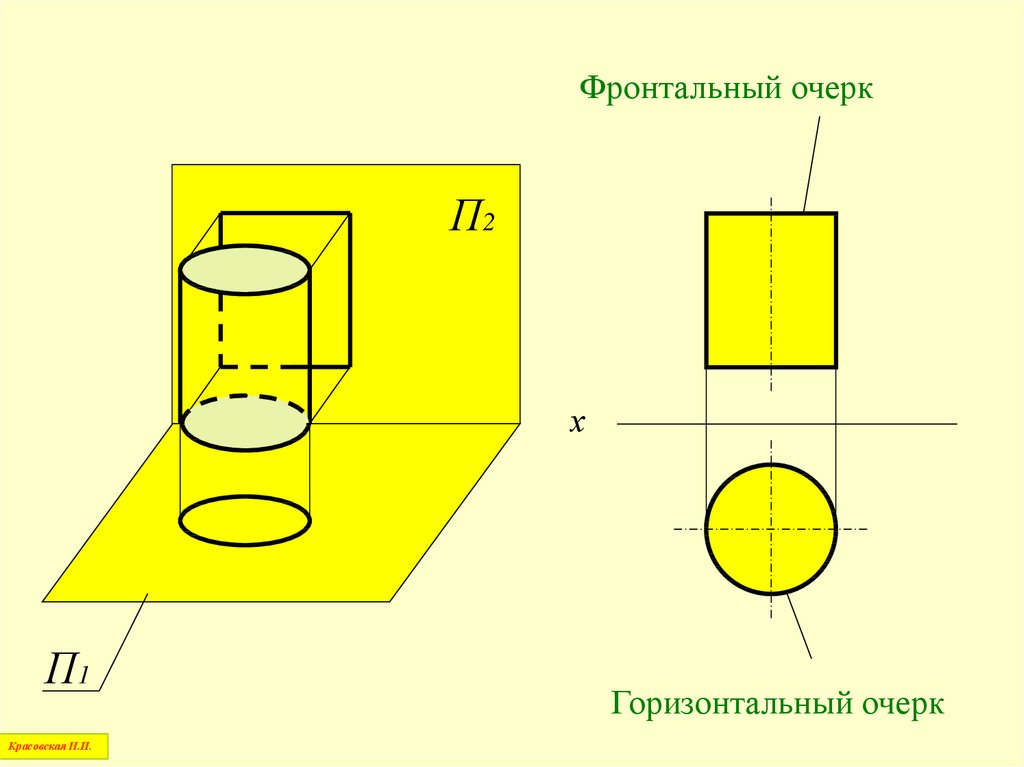
Очерк поверхностипри ортогональном проецировании –
это линия, ограничивающая проекцию
поверхности на плоскостях проекций
Красовская Н.И.
15.
Фронтальный очеркП2
х
П1
Красовская Н.И.
Горизонтальный очерк
16.
Классификацияповерхностей
Красовская Н.И.
17.
По виду образующей все поверхности можноразделить на
линейчатые
и
нелинейчатые
Красовская Н.И.
18.
У линейчатых поверхностей образующейявляется прямая линия,
у нелинейчатых – кривая линия
Красовская Н.И.
19.
Линейчатыеповерхности
Красовская Н.И.
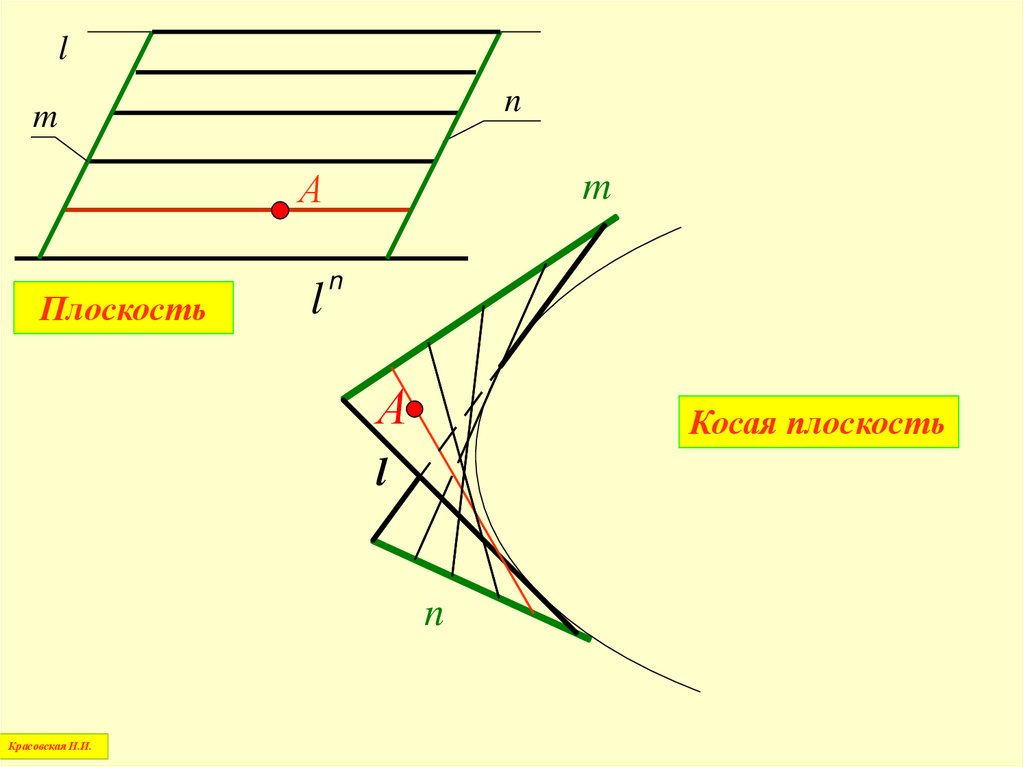
20.
ln
m
А
Плоскость
l
m
n
А
Косая плоскость
l
n
Красовская Н.И.
21.
Коническая поверхностьS
l
Цилиндрическая
поверхность
А
l
А
s
m
m
Красовская Н.И.
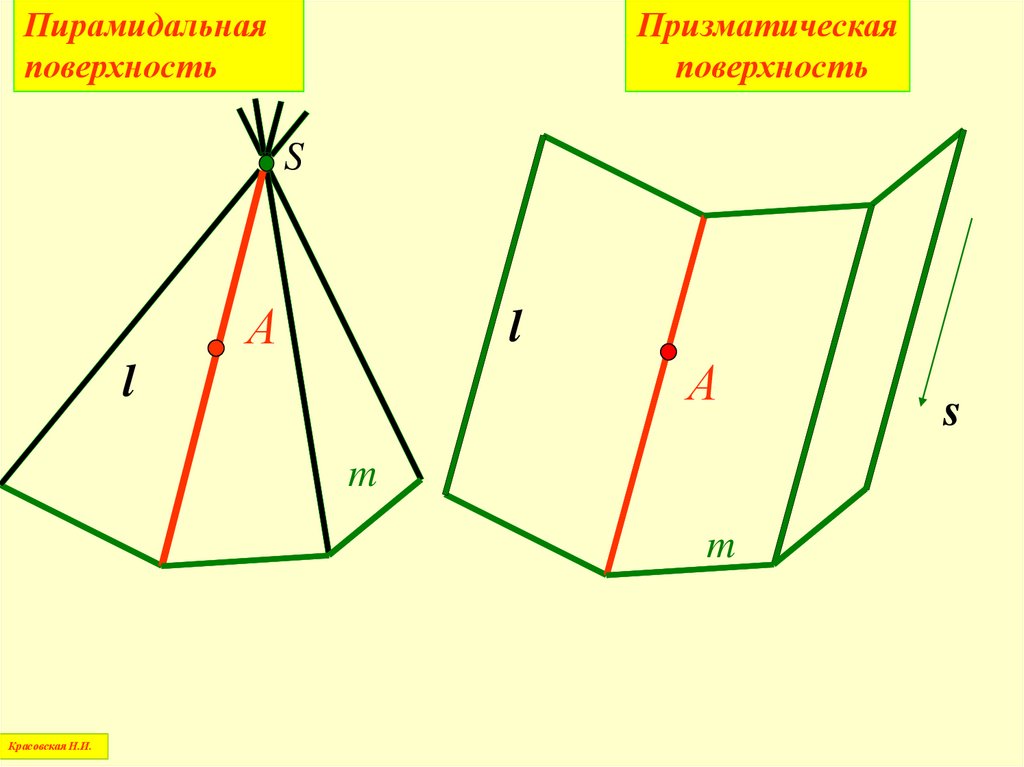
22.
Пирамидальнаяповерхность
Призматическая
поверхность
S
А
l
А
l
m
m
Красовская Н.И.
s
23.
Точка принадлежит поверхности,если она лежит на какой – нибудь
линии этой поверхности
Линия
принадлежит поверхности,
если все ее точки принадлежат этой
поверхности
Красовская Н.И.
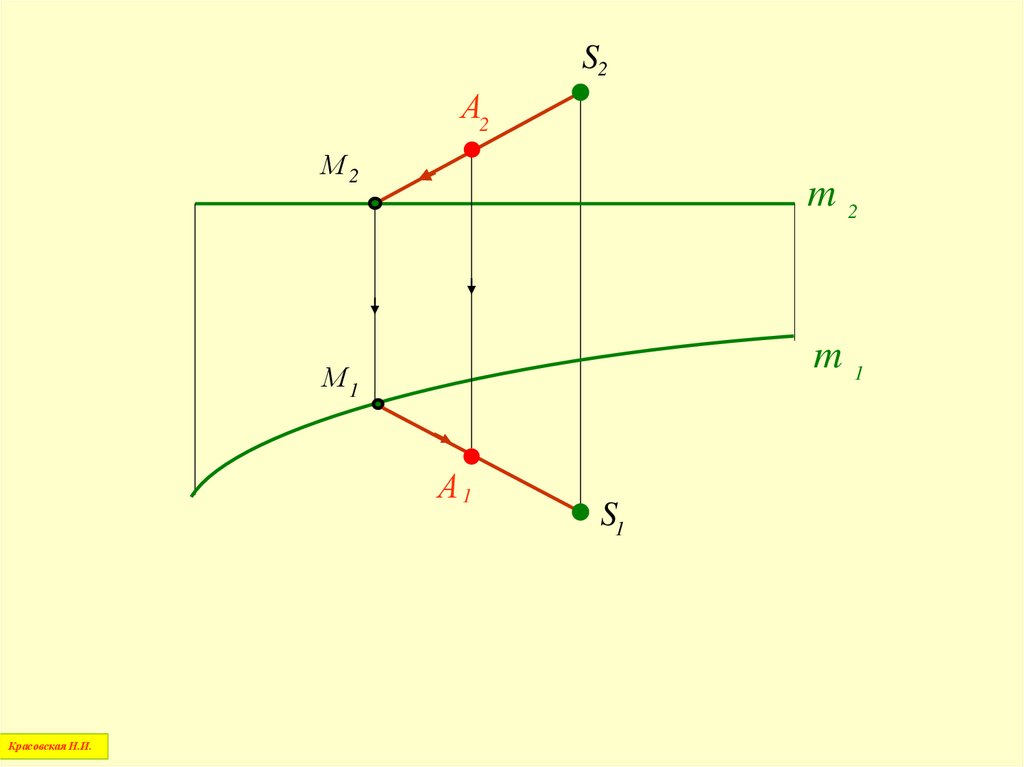
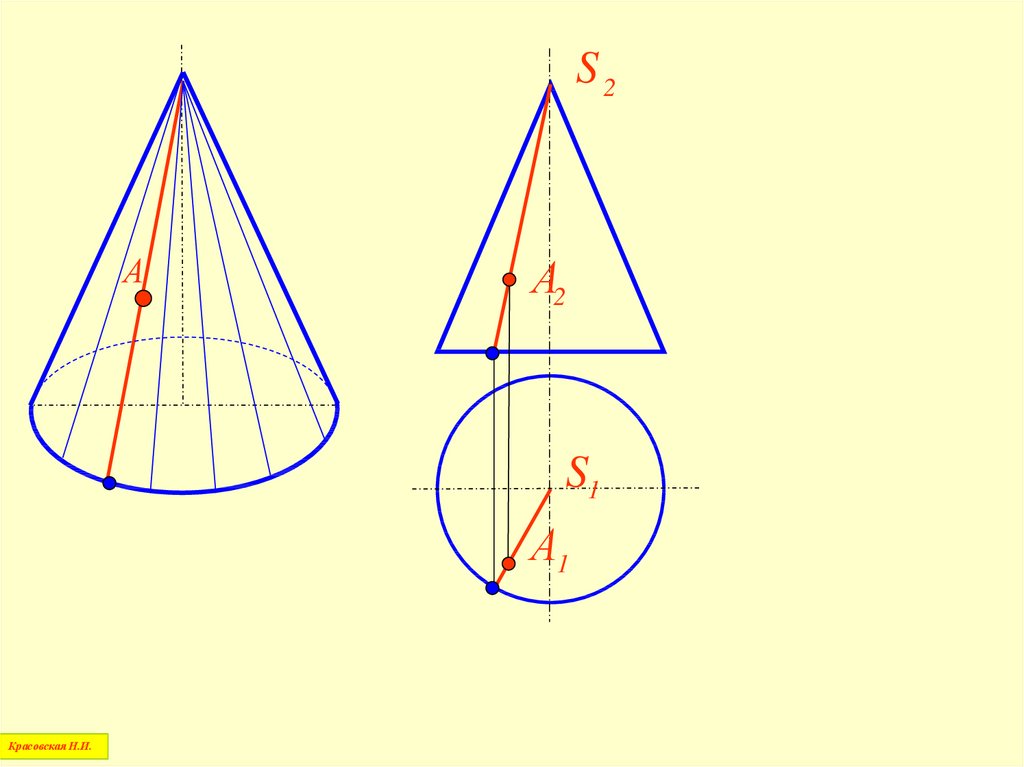
24.
S2А2
М2
m2
m1
М1
А1
Красовская Н.И.
S1
25.
Алгоритмпостроения недостающей проекции точки,
принадлежащей линейчатой поверхности
1. Через заданную проекцию точки, лежащей на поверхности,
проводится проекция простейшей линии, принадлежащей этой
поверхности
2. Строится вторая проекция этой линии
из условия ее принадлежности данной поверхности
3. По линии проекционной связи на построенной проекции линии
находится искомая проекция заданной точки
Красовская Н.И.
26.
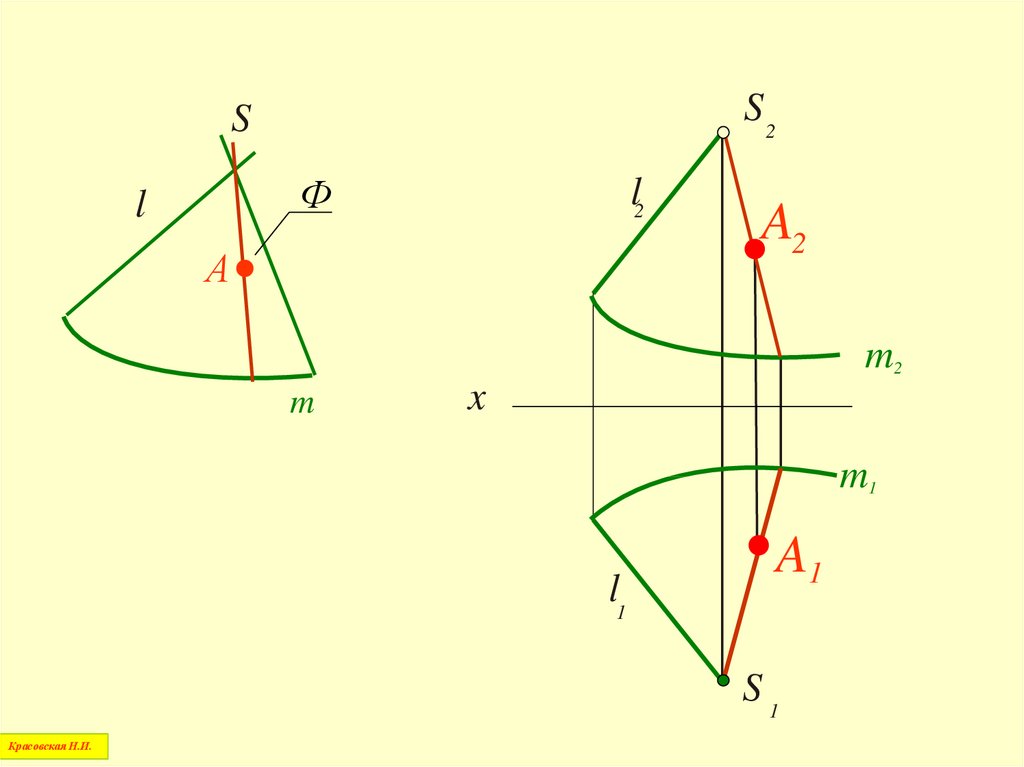
S2S
Ф
l
l2
А
A2
m2
m
x
m1
l1
A1
S1
Красовская Н.И.
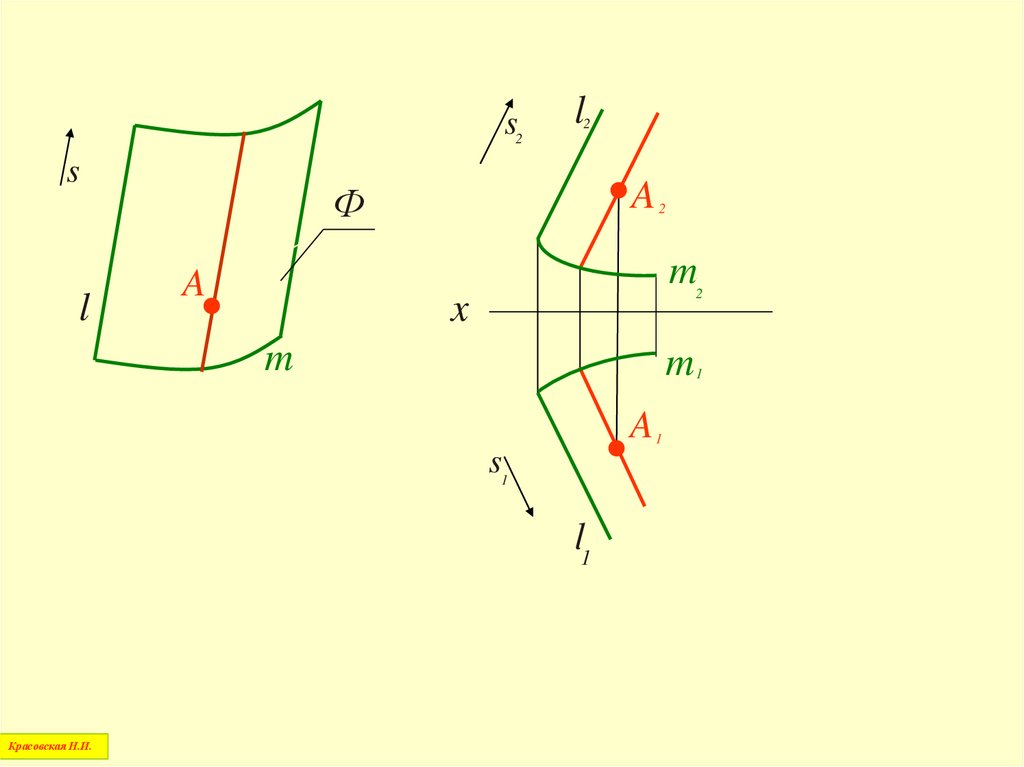
27.
s2s
l
l
2
A
Ф
2
m
A
2
x
m
m
A
s1
l1
Красовская Н.И.
1
1
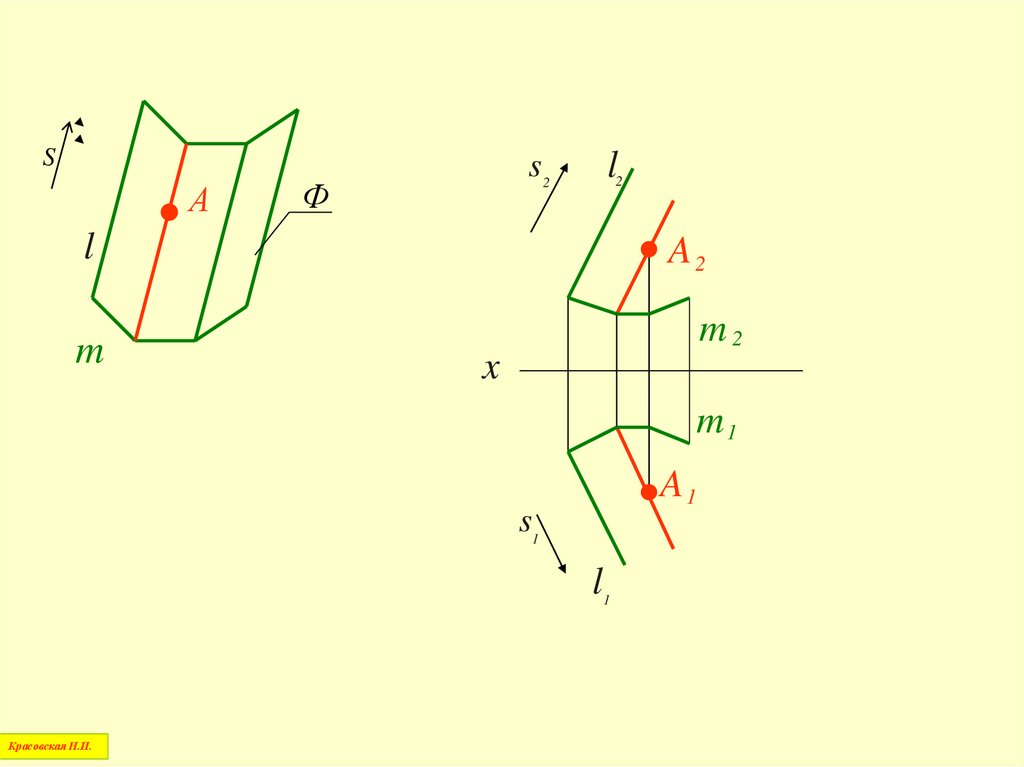
28.
l2 S2S
Ф
l
A2
A
m
m2
x
m1
A1
l1
S
1
Красовская Н.И.
29.
SА
l
s2
Ф
2
l
m
A2
m2
x
m1
A1
s1
l
Красовская Н.И.
1
30.
Таким образом,через каждую точку линейчатой
поверхности можно всегда провести
прямую линию
Красовская Н.И.
31.
МногогранникиКрасовская Н.И.
32.
Многогранник –замкнутая пространственная фигура,
ограниченная плоскими
многоугольниками
Красовская Н.И.
33.
Если все вершины и ребра многогранниканаходятся по одну сторону плоскости
любой его грани,
то многогранник называется
выпуклым
Красовская Н.И.
34.
Правильные многогранники –это фигуры, у которых все грани являются
правильными и конгруэнтными
многоугольниками, а многогранные углы при
вершинах – выпуклые и содержат одинаковое
количество граней.
(Все правильные многогранники можно
вписать в сферу)
Красовская Н.И.
35.
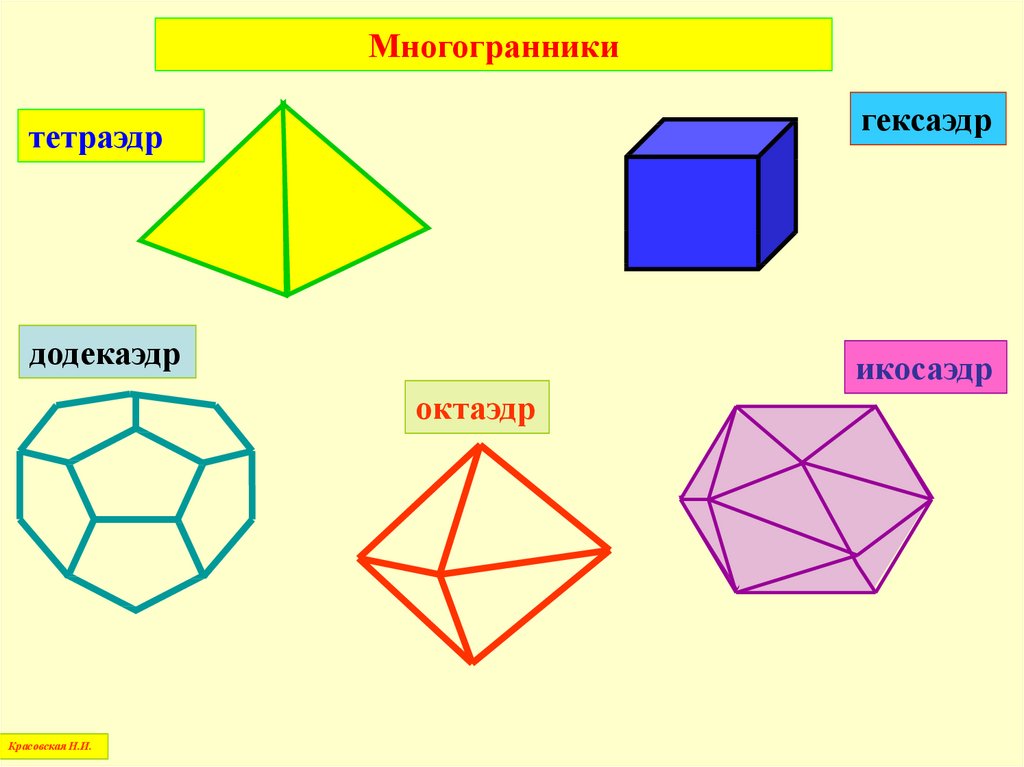
Правильными многогранникамиявляются:
тетраэдр – правильный четырехгранник,
гексаэдр – правильный шестигранник,
октаэдр – правильный восьмигранник,
додекаэдр – правильный двенадцатигранник,
икосаэдр – правильный двадцатигранник
Красовская Н.И.
36.
Многогранникитетраэдр
гексаэдр
додекаэдр
икосаэдр
октаэдр
Красовская Н.И.
37.
Пирамида –это многогранник, одна грань которого –
многоугольник, а остальные –
треугольники с общей вершиной
Красовская Н.И.
38.
Правильная пирамида –это пирамида, у которой основание является
правильным многоугольником, а высота
проходит через центр этого многоугольника
Красовская Н.И.
39.
S2М2
М2
12
S1
Красовская Н.И.
М1
11
М1
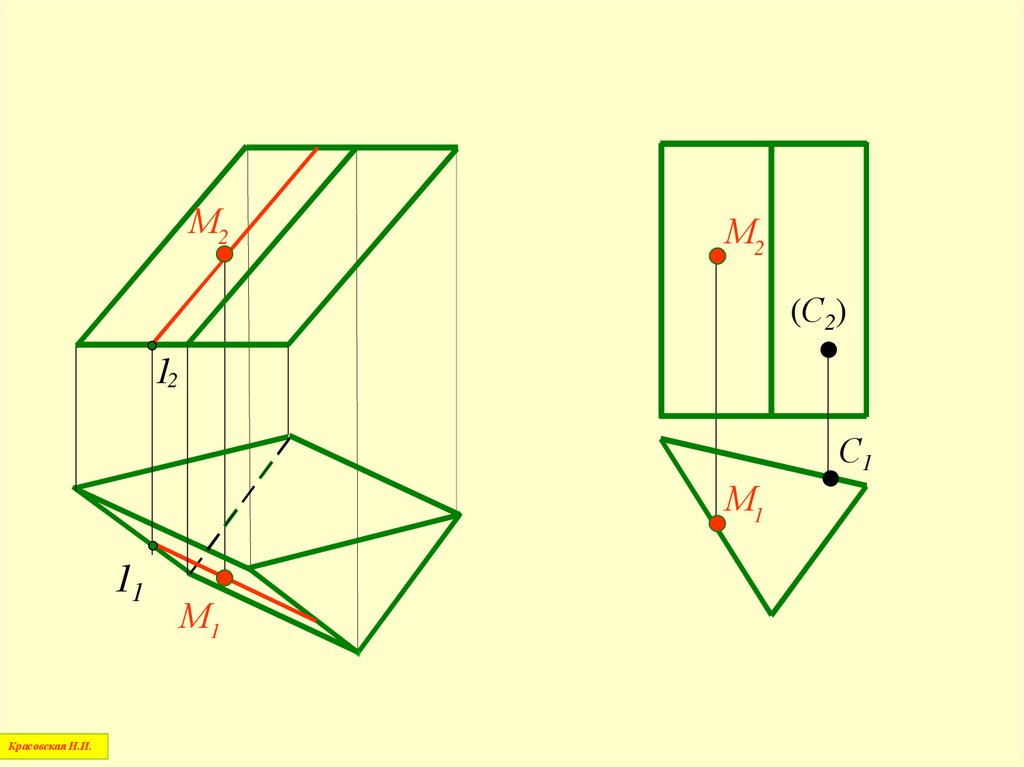
40.
Призма– это многогранник, две грани которого
представляют собой равные многоугольники
с взаимно параллельными сторонами, а все
другие грани – параллелограммы
Красовская Н.И.
41.
Прямая призма– призма, ребра которой перпендикулярны
к плоским основаниям
Красовская Н.И.
42.
М2М2
(С2)
12
С1
М1
11
Красовская Н.И.
М1
43.
Поверхностивращения
Красовская Н.И.
44.
У поверхности вращениягеометрическая часть определителя
состоит из
образующей l и оси вращения i:
Ф (l,i)[A]
Красовская Н.И.
45.
Плоскости, перпендикулярные к осивращения, пересекают поверхность по
окружностям, которые называются
параллелями
Радиус каждой параллели измеряется
от оси до очерка
от оси до очерка !!!
Красовская Н.И.
46.
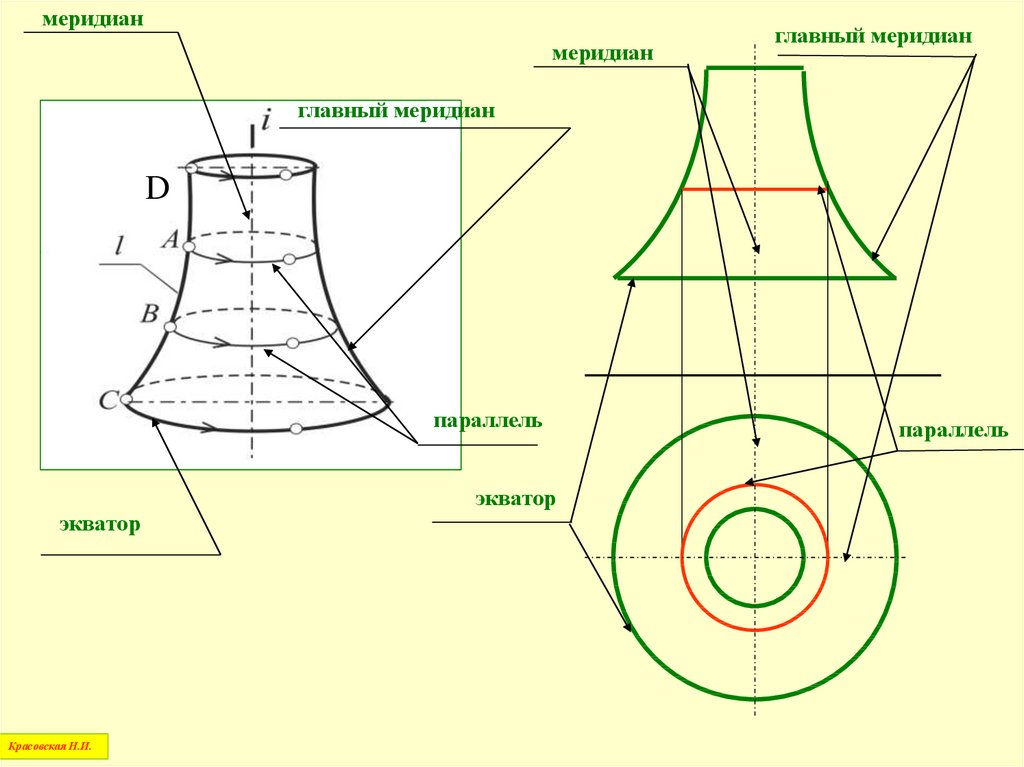
Наибольшую из параллелей называютэкватором,
наименьшую –
горлом
Красовская Н.И.
47.
Плоскость, проходящая через осьповерхности вращения, называется
меридиональной,
а линия пересечения поверхности с этой
плоскостью называется
меридианом
поверхности
Красовская Н.И.
48.
Если меридиональная плоскость параллельнафронтальной плоскости проекций П2,
то в сечении получается меридиан, который
называется
главным меридианом
Красовская Н.И.
49.
меридианмеридиан
главный меридиан
главный меридиан
D
параллель
экватор
экватор
Красовская Н.И.
параллель
50.
51.
Примеры поверхностейвращения
Красовская Н.И.
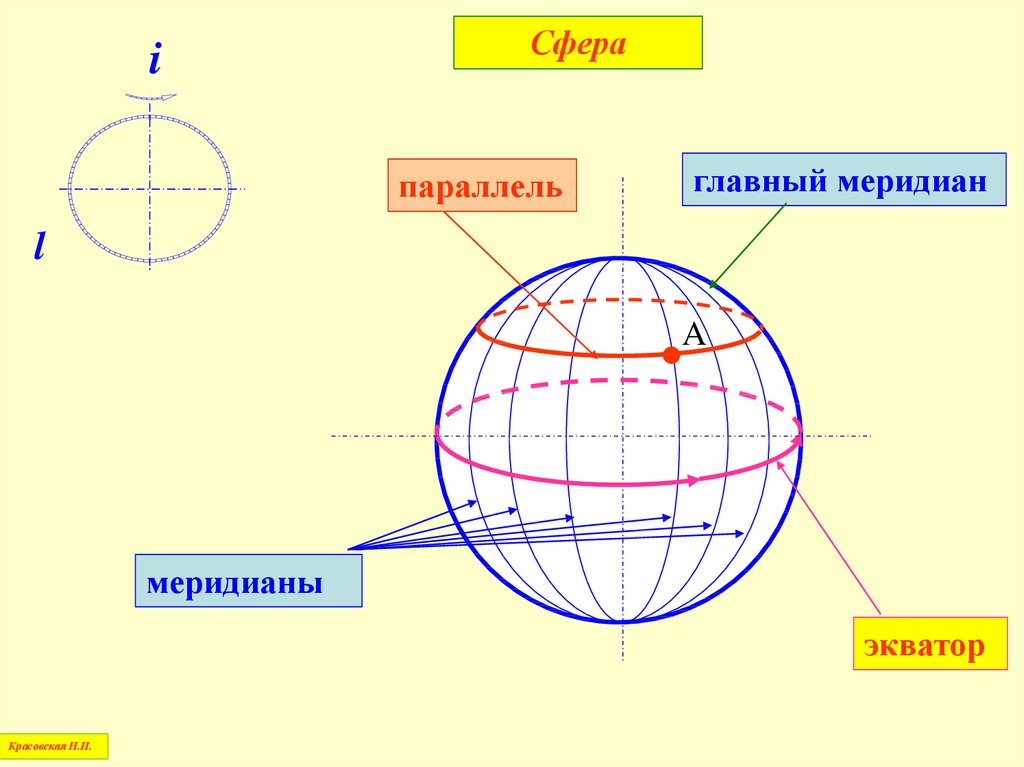
52.
iСфера
параллель
главный меридиан
l
A
меридианы
экватор
Красовская Н.И.
53.
видео54.
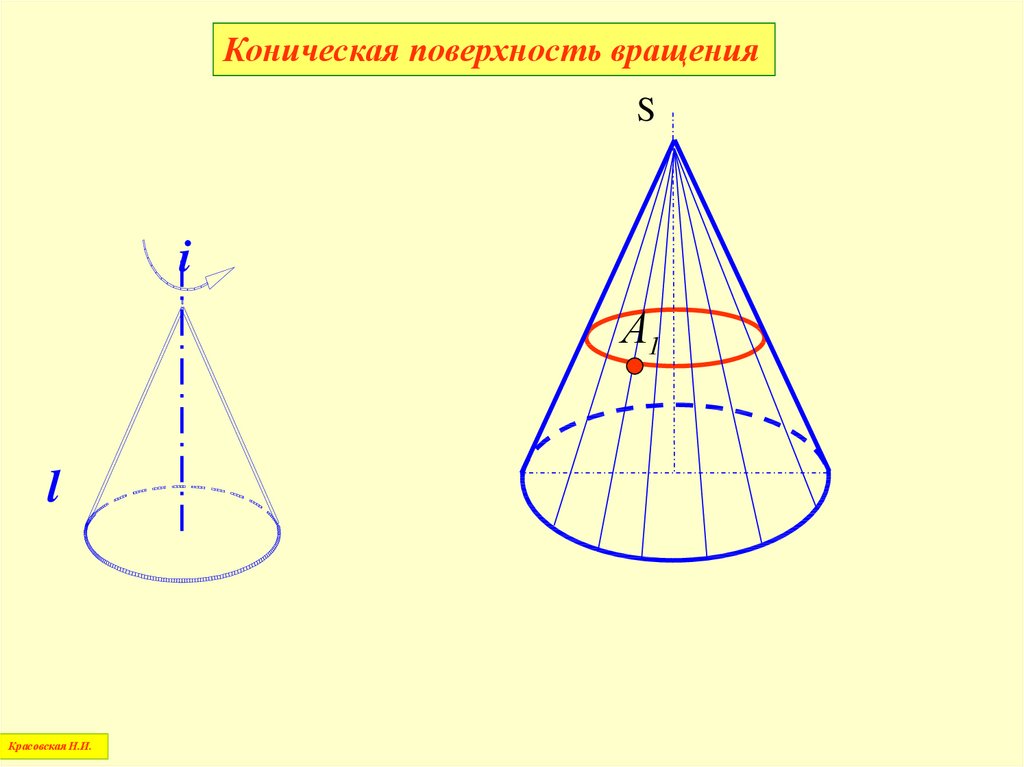
Коническая поверхность вращенияS
i
А1
l
Красовская Н.И.
55.
56.
Цилиндрическая поверхность вращенияi
l
А1
Красовская Н.И.
57.
58.
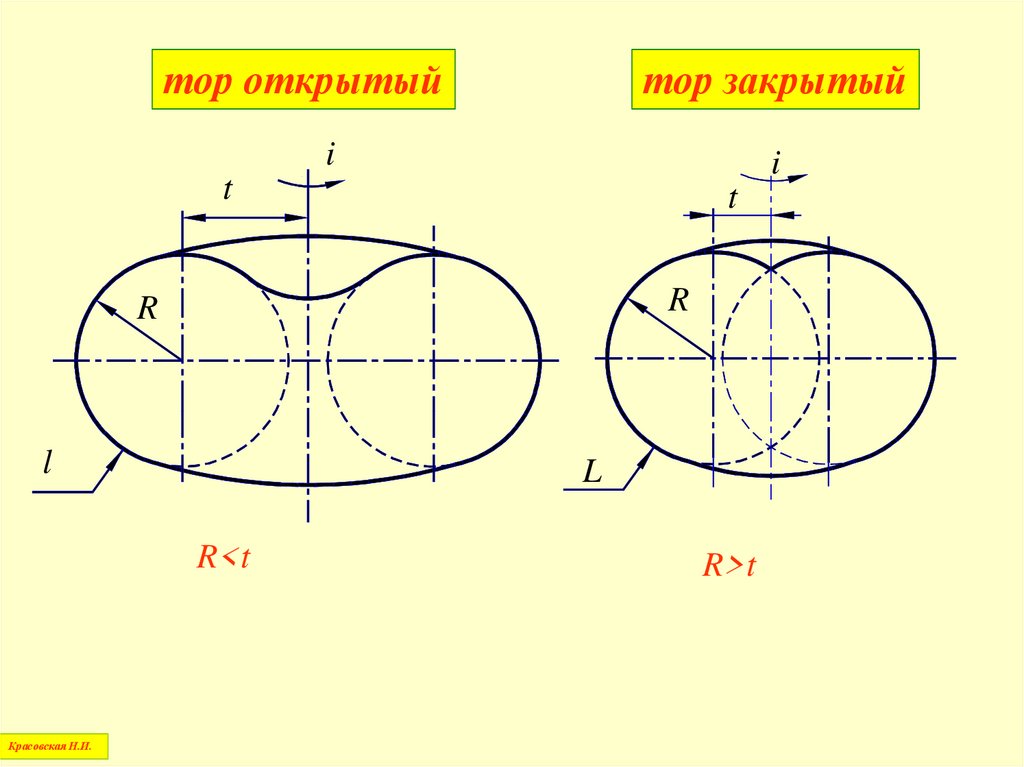
тор открытыйтор закрытый
i
i
t
t
R
R
l
L
R<t
Красовская Н.И.
R>t
59.
60.
61.
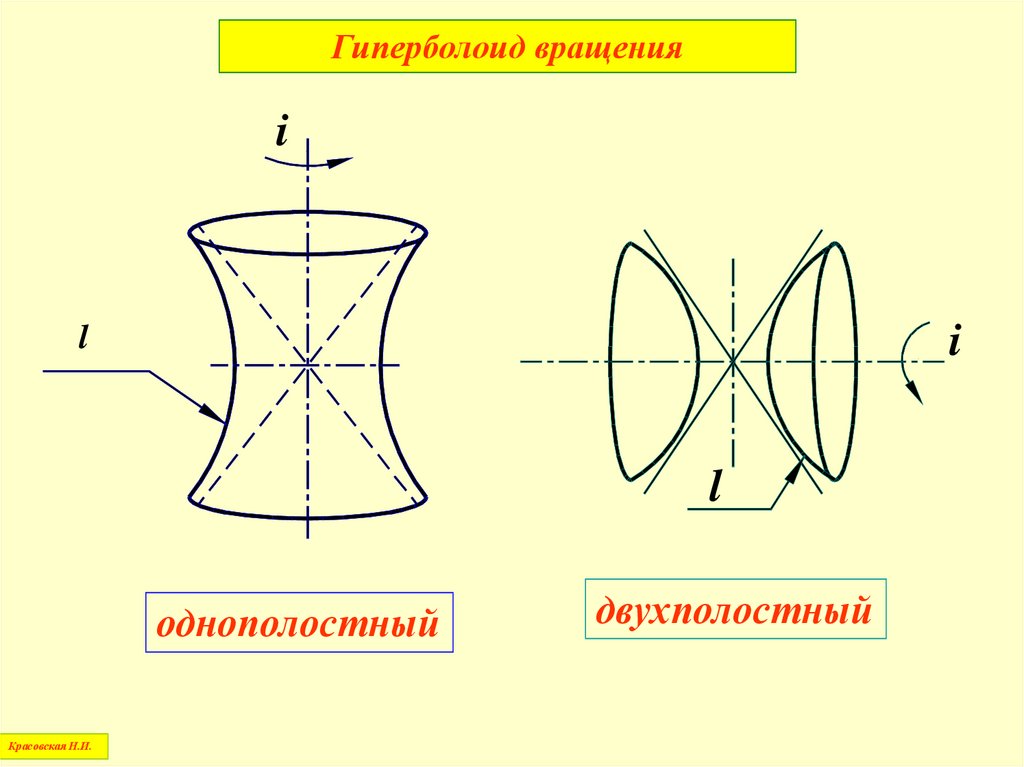
Гиперболоид вращенияi
i
l
l
однополостный
Красовская Н.И.
двухполостный
62.
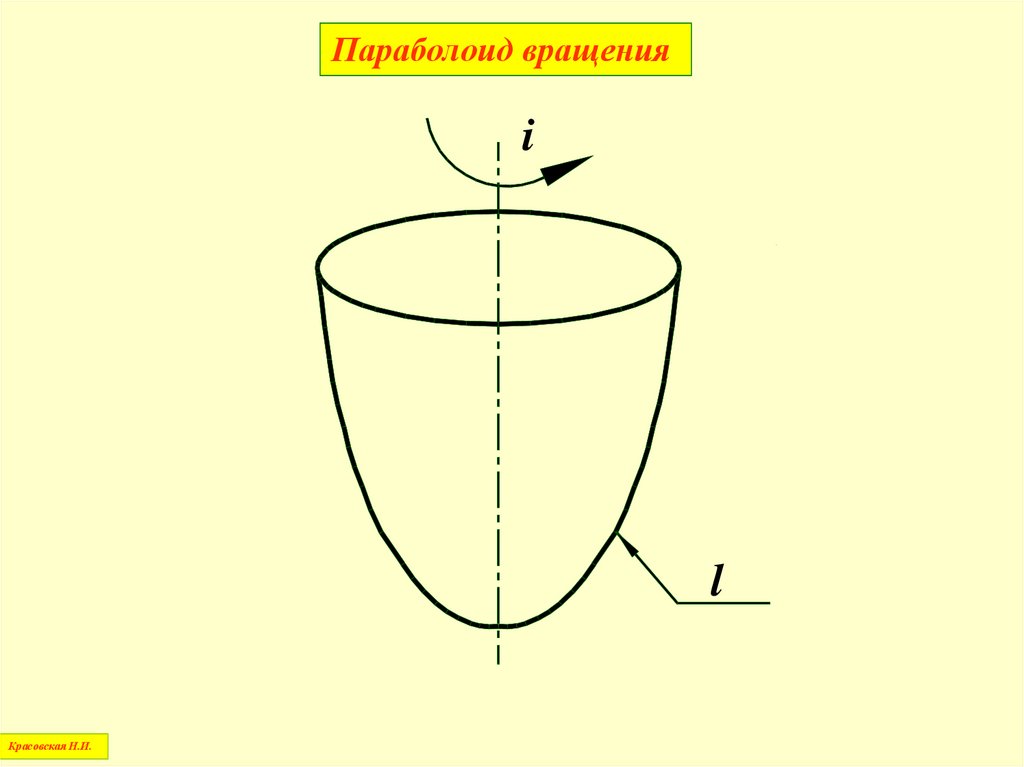
Параболоид вращенияi
l
Красовская Н.И.
63.
ЭллипсоидКрасовская Н.И.
64.
RA2
A1
Красовская Н.И.
65.
Алгоритмрешения задач на принадлежность точки поверхности
вращения
1. Через заданную проекцию точки проводят
проекцию вспомогательной параллели
2. Строят вторую проекцию этой параллели, измеряя ее радиус от
оси вращения до очерка поверхности
от оси до очерка !!!
3. По линии проекционной связи на построенной
проекции параллели находят недостающую проекцию
точки с учетом ее видимости
Красовская Н.И.
66.
Построение точкина поверхности
сферы
Красовская Н.И.
67.
А2(А3)
R
R
А1
Красовская Н.И.
68.
Построение точкина поверхности прямого
кругового конуса
Красовская Н.И.
69.
S2А
А2
S1
А1
Красовская Н.И.
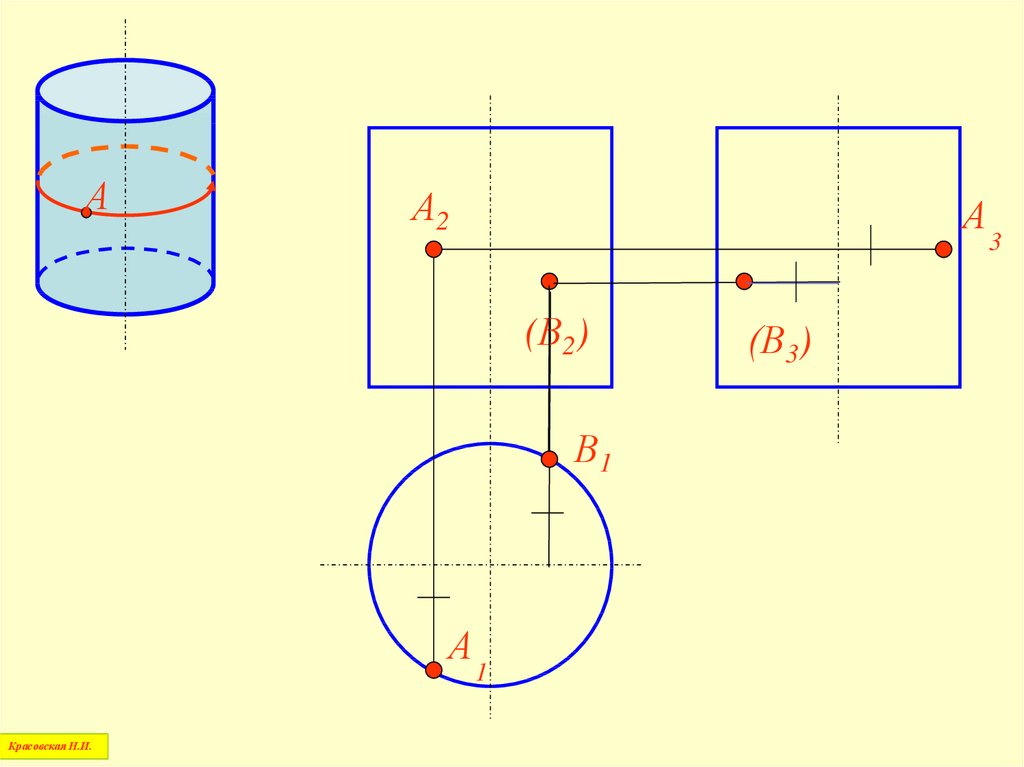
70.
А2(В2)
А
В1
А1
Красовская Н.И.
А3
В3
71.
Построение точкина поверхности прямого
кругового цилиндра
Красовская Н.И.
72.
АА2
А
(В2)
В1
А
Красовская Н.И.
1
(В3)
3
73.
ТОРКрасовская Н.И.
74.
i2А2
(А1)
i
1
Красовская Н.И.
75.
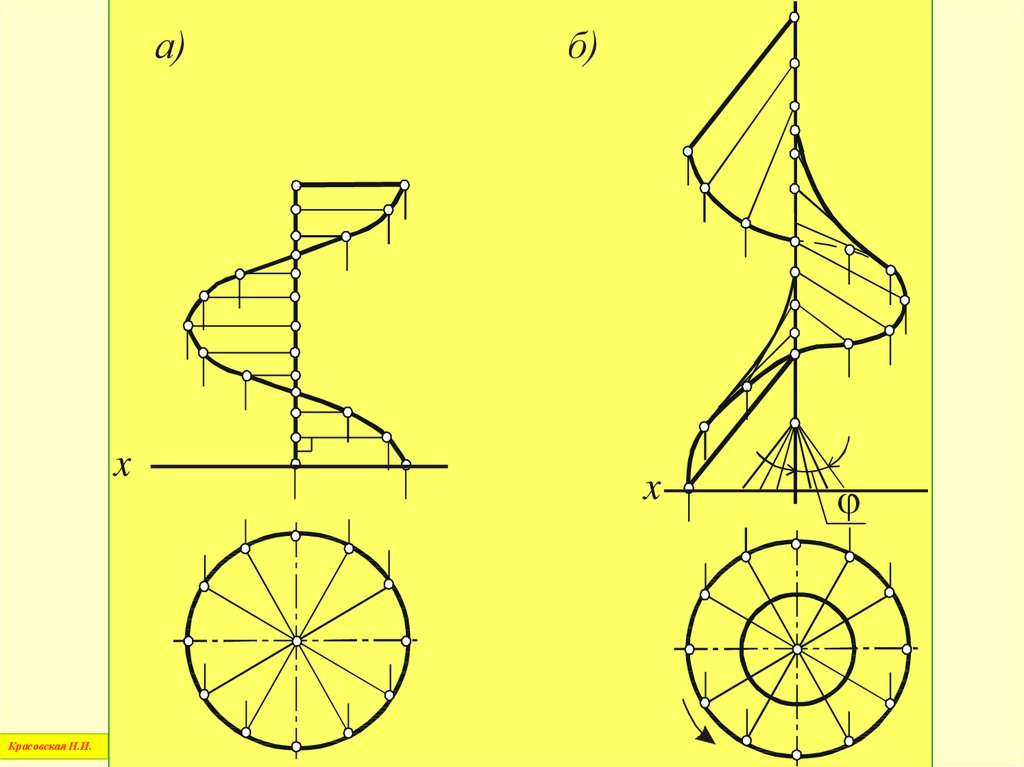
Винтовые поверхностиКрасовская Н.И.
76.
Все точки винтовой поверхности совершаютвинтовые движения, описывая
винтовые линии – гелисы,
а поверхности называются
геликоидами
Красовская Н.И.
77.
Прямые геликоиды,если угол наклона образующей
равен 90
Наклонные - если угол
не равен 90
Красовская Н.И.
78.
а)x
Красовская Н.И.
б)
x
79.
Выводы:- поверхность может быть получена вращением некоторой
образующей вокруг оси или движением ее по направляющей
- поверхность может быть задана на чертеже проекциями элементов
геометрической части ее определителя или
для достижения большей наглядности – очерком
- поверхности могут быть систематизированы в зависимости от вида
образующих и направляющих, а также от закона движения образующих
- для нахождения недостающей проекции точки, лежащей на
поверхности, пользуются характерными для данной поверхности
простейшими линиями
Красовская Н.И.
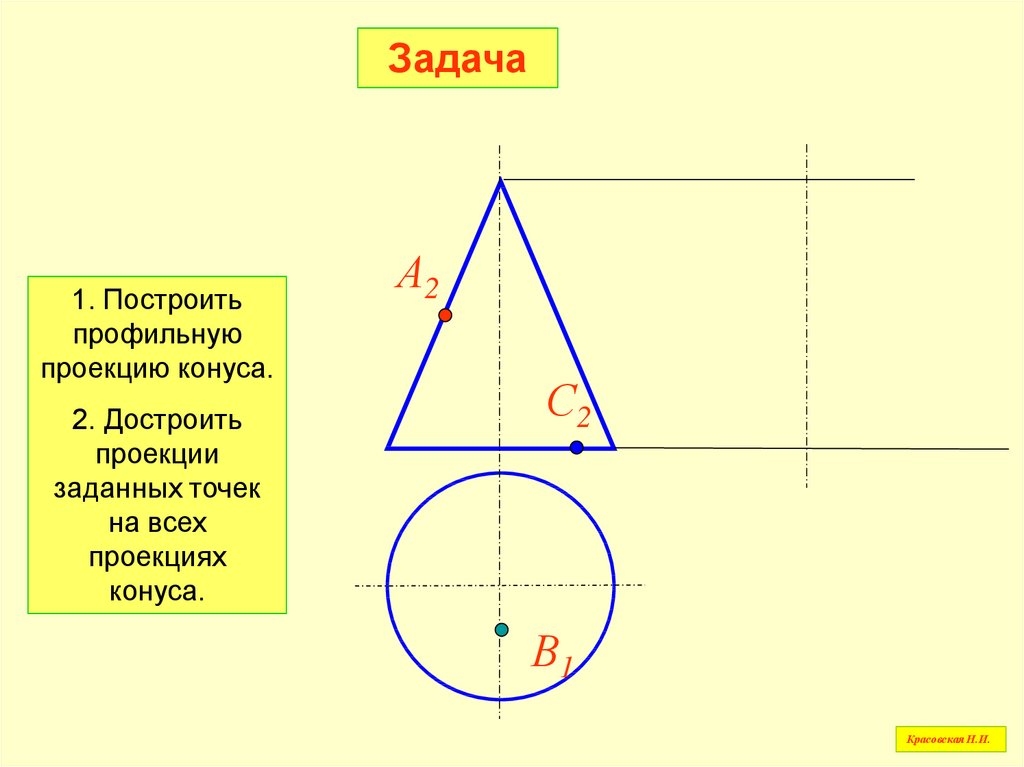
80.
Задача1. Построить
профильную
проекцию конуса.
2. Достроить
проекции
заданных точек
на всех
проекциях
конуса.
А2
С2
В1
Красовская Н.И.

























































 drafting
drafting








