Гранные и кривые поверхности. (Лекция 6)

1.

Лекция №6
Поверхности.
Образование и задание гранных и
кривых поверхностей
Построение проекций точек на
гранных и кривых поверхностях

2.

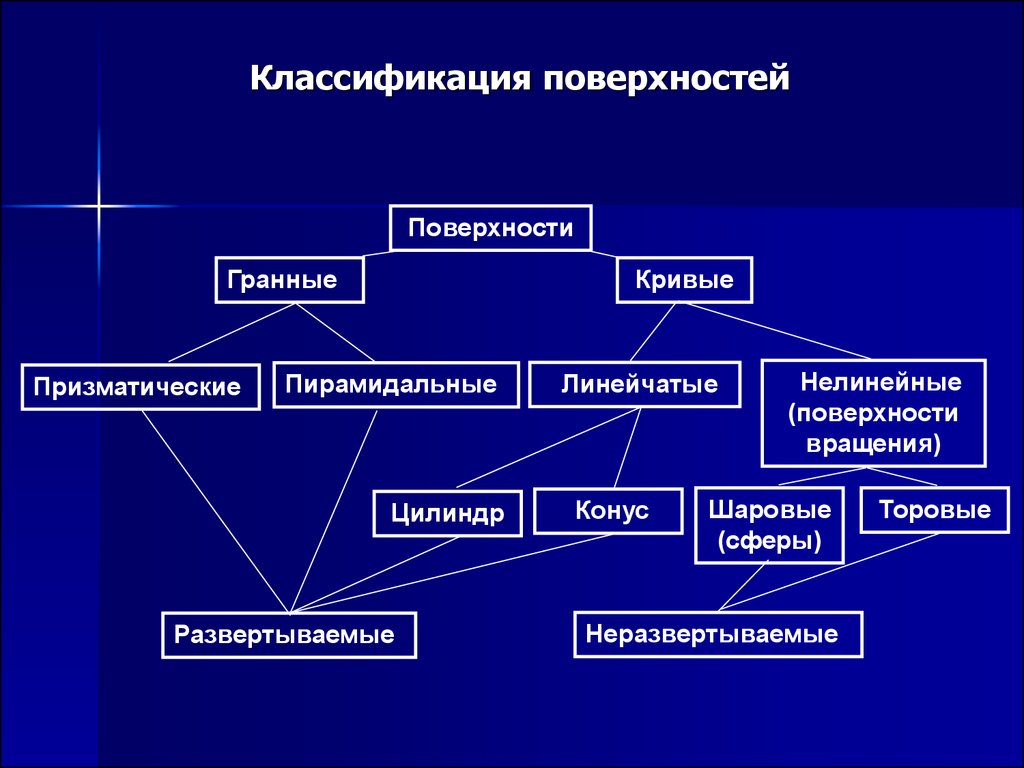
Классификация поверхностей
Поверхности
Гранные
Призматические
Кривые
Пирамидальные
Цилиндр
Развертываемые
Линейчатые
Конус
Нелинейные
(поверхности
вращения)
Шаровые
(сферы)
Неразвертываемые
Торовые

3. Гранные поверхности

Гранные поверхности (многогранники) образуются перемещением прямой
линии, которая называется образующей, по определенной закономерности.
Проецирование призматической поверхности и точек, на ней
лежащих
S
L
m
m – направляющая призматической поверхности;
S – направление образующих поверхности;
L – образующая поверхности;
Ø(m, L) – математический определитель призматической поверхности;
[L ∩ m; L S] – геометрический определитель
призматической поверхности

4.

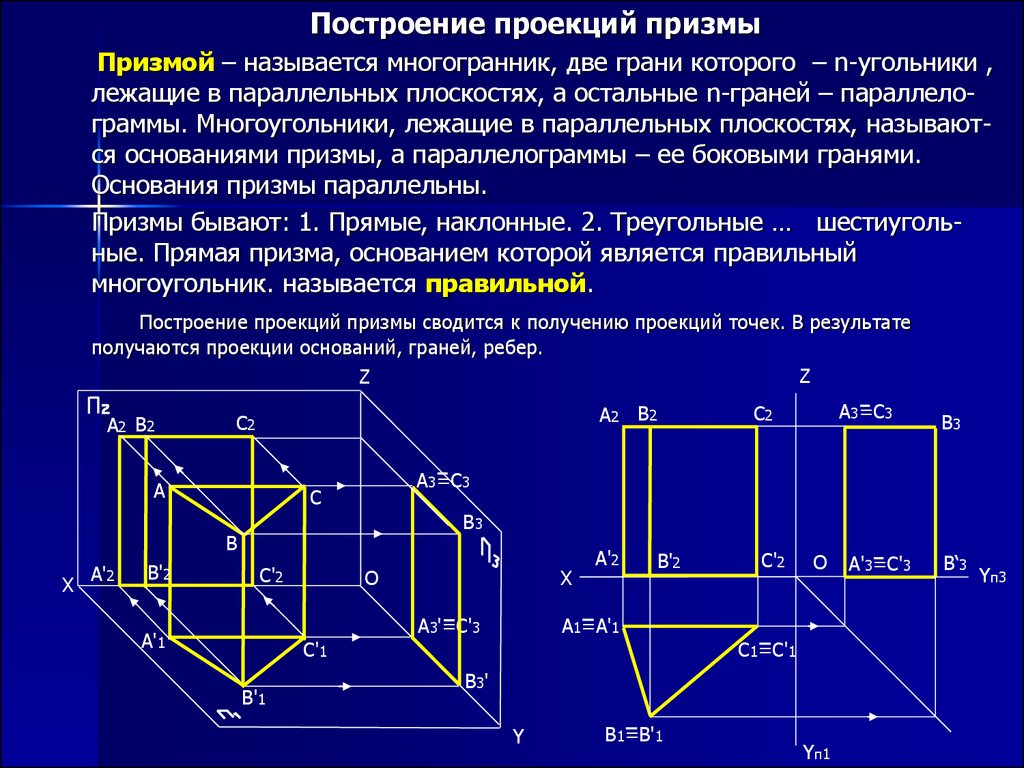
Построение проекций призмы
Призмой – называется многогранник, две грани которого – n-угольники ,
лежащие в параллельных плоскостях, а остальные n-граней – параллелограммы. Многоугольники, лежащие в параллельных плоскостях, называются основаниями призмы, а параллелограммы – ее боковыми гранями.
Основания призмы параллельны.
Призмы бывают: 1. Прямые, наклонные. 2. Треугольные … шестиугольные. Прямая призма, основанием которой является правильный
многоугольник. называется правильной.
Построение проекций призмы сводится к получению проекций точек. В результате
получаются проекции оснований, граней, ребер.
Z
Z
А2 В2
A2 В2
С2
A
X
В'2
В3
А3=С3
С
В3
В
A'2
А3=С3
С2
С'2
A'1
O
С'1
В'1
X
А3'=С'3
A'2
В'2
A1=A'1
С'2
O
C1=C'1
В3'
Y
B1=B'1
Yп1
А'3=С'3
В‘3
Yп3

5.

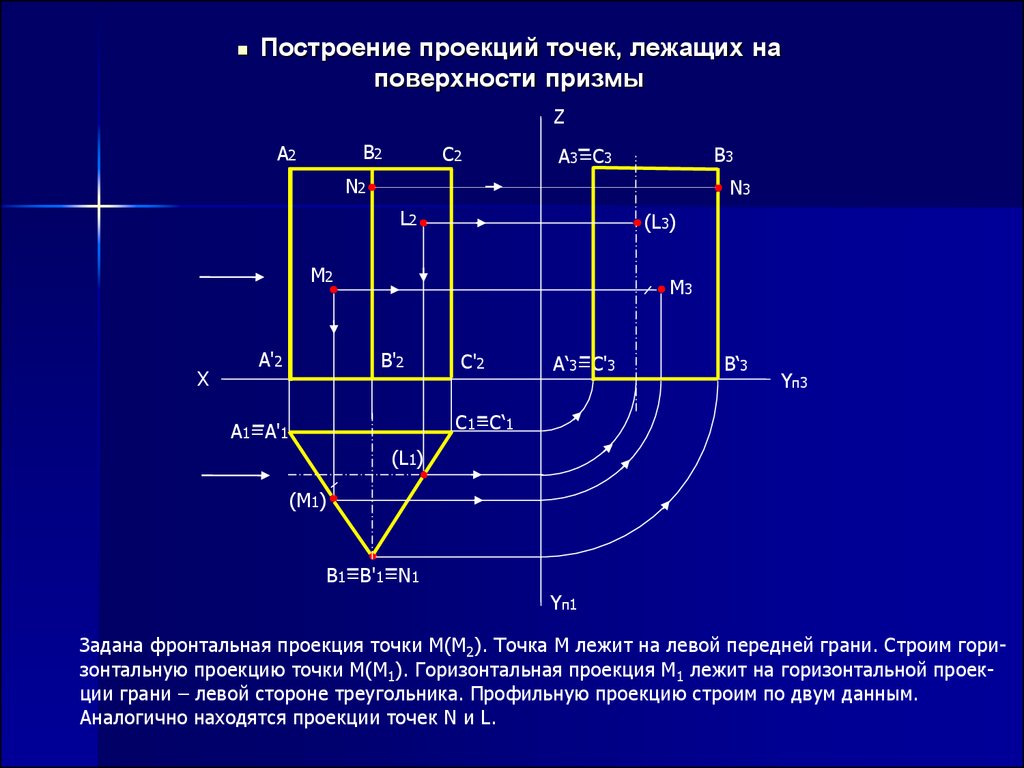
Построение проекций точек, лежащих на
поверхности призмы
Z
В2
A2
С2
В3
А3=С3
N2
N3
L2
(L3)
M2
X
A'2
M3
В'2
С'2
А‘3=С'3
В‘3
Yп3
С1=С‘1
А1=А'1
(L1)
(M1)
В1=В'1=N1
Yп1
Задана фронтальная проекция точки М(М2). Точка М лежит на левой передней грани. Строим горизонтальную проекцию точки М(М1). Горизонтальная проекция М1 лежит на горизонтальной проекции грани – левой стороне треугольника. Профильную проекцию строим по двум данным.
Аналогично находятся проекции точек N и L.

6.

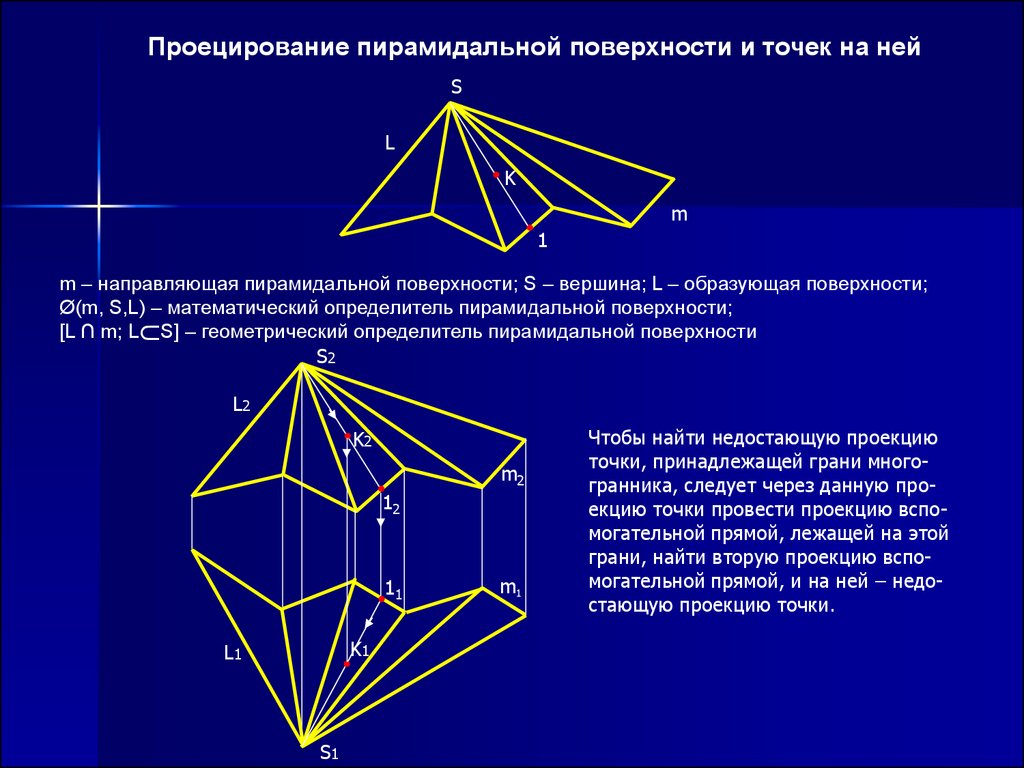
Проецирование пирамидальной поверхности и точек на ней
S
L
K
m
1
∩
m – направляющая пирамидальной поверхности; S – вершина; L – образующая поверхности;
Ø(m, S,L) – математический определитель пирамидальной поверхности;
[L ∩ m; L S] – геометрический определитель пирамидальной поверхности
S2
L2
K2
m2
12
11
K1
L1
S1
m1
Чтобы найти недостающую проекцию
точки, принадлежащей грани многогранника, следует через данную проекцию точки провести проекцию вспомогательной прямой, лежащей на этой
грани, найти вторую проекцию вспомогательной прямой, и на ней – недостающую проекцию точки.

7.

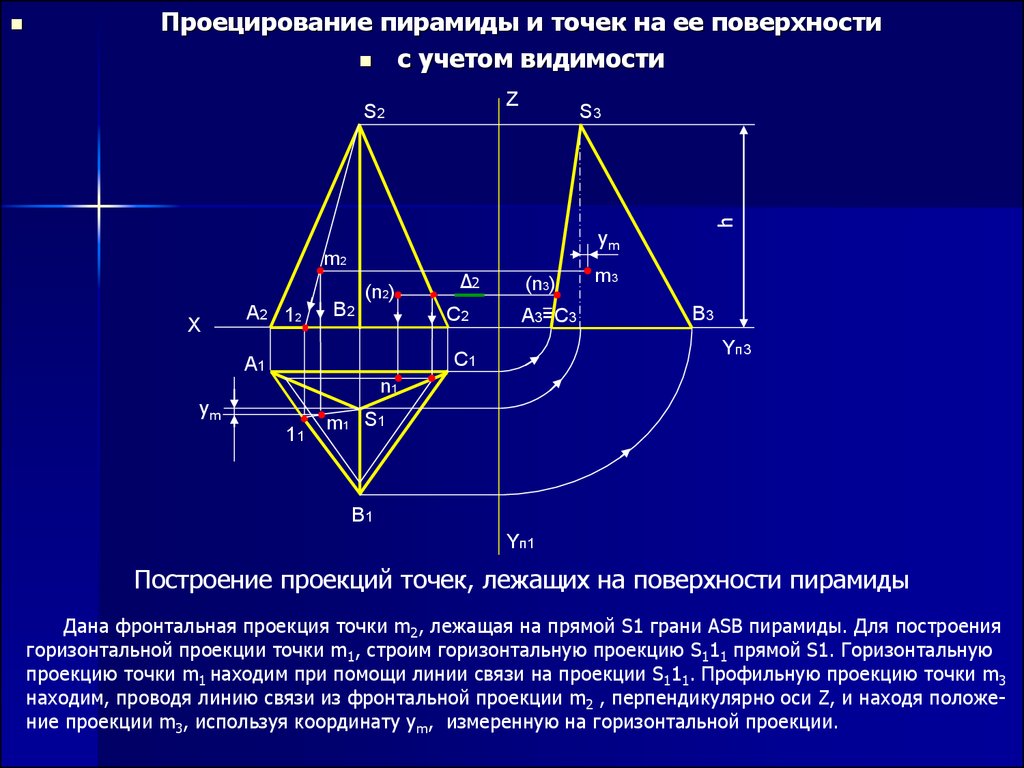
Проецирование пирамиды и точек на ее поверхности
с учетом видимости
Z
S2
ym
m2
Х
A2 12
S3
В2
(n2)
Δ2
С2
(n3)
A3=C3
m3
B3
Yп3
С1
A1
h
n1
ym
11
m1 S1
В1
Yп1
Построение проекций точек, лежащих на поверхности пирамиды
Дана фронтальная проекция точки m2, лежащая на прямой S1 грани АSB пирамиды. Для построения
горизонтальной проекции точки m1, строим горизонтальную проекцию S111 прямой S1. Горизонтальную
проекцию точки m1 находим при помощи линии связи на проекции S111. Профильную проекцию точки m3
находим, проводя линию связи из фронтальной проекции m2 , перпендикулярно оси Z, и находя положение проекции m3, используя координату уm, измеренную на горизонтальной проекции.

8. Кривые поверхности

Кривые поверхности в начертательной геометрии рассматриваются как кинематические: их поверхности образуются непрерывным перемещением линии, называемой образующей, по определенному закону. Образующая может сохранять свою форму при изменении положения, или непрерывно изменять как
форму, так и положение.
Все кривые поверхности делятся на две основные группы:
А. Поверхности, образующиеся движением прямой линии в пространстве. Они
называются линейчатыми. Это цилиндр, конус, цилиндроид, коноид и др.
Б. Поверхности, образованные движением только кривой линии. Они
называются нелинейчатыми или криволинейными. Это сфера, тор, эллипсоид,
параболоид и гиперболоид вращения и др.

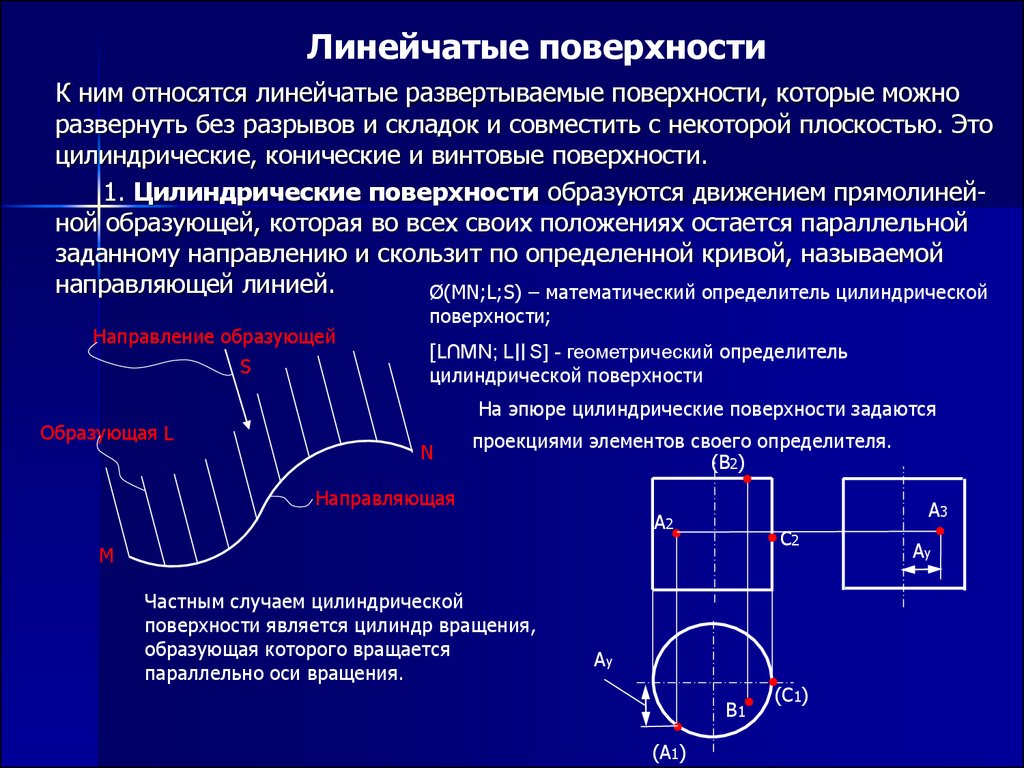
9. Линейчатые поверхности

К ним относятся линейчатые развертываемые поверхности, которые можно
развернуть без разрывов и складок и совместить с некоторой плоскостью. Это
цилиндрические, конические и винтовые поверхности.
1. Цилиндрические поверхности образуются движением прямолинейной образующей, которая во всех своих положениях остается параллельной
заданному направлению и скользит по определенной кривой, называемой
направляющей линией.
Ø(MN;L;S) – математический определитель цилиндрической
Направление образующей
S
поверхности;
[L∩MN; L S] - геометрический определитель
цилиндрической поверхности
На эпюре цилиндрические поверхности задаются
Образующая L
N
проекциями элементов своего определителя.
(В2)
Направляющая
А3
А2
С2
M
Частным случаем цилиндрической
поверхности является цилиндр вращения,
образующая которого вращается
параллельно оси вращения.
Аy
В1
(А1)
(С1)
Аy

10.

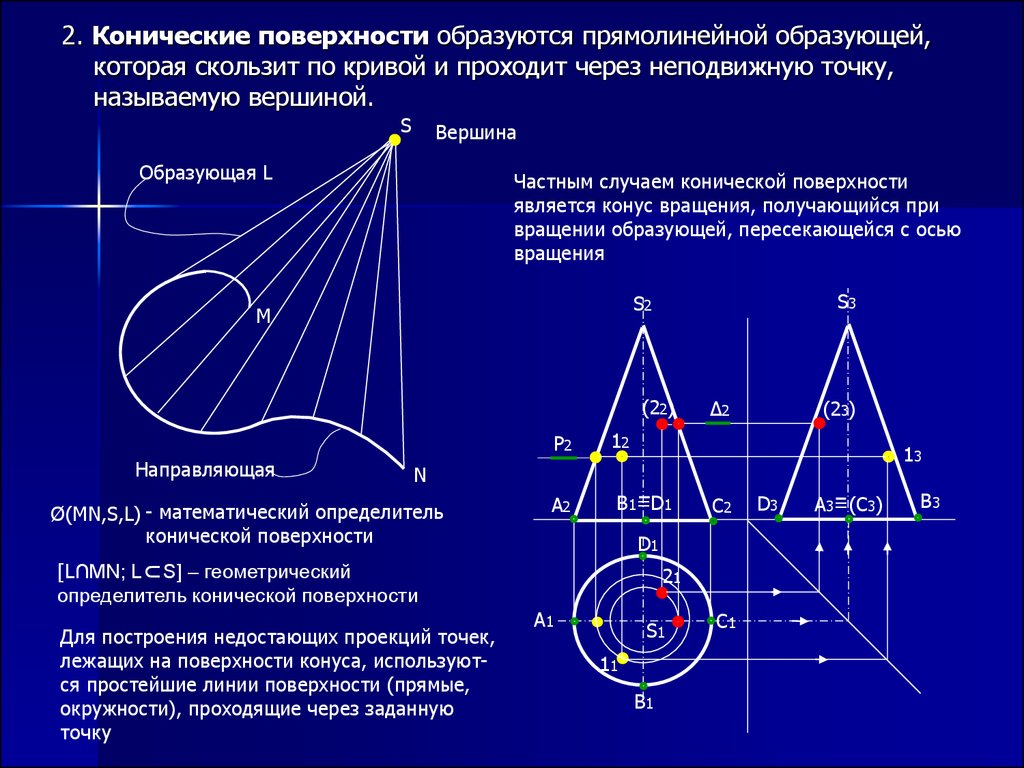
2. Конические поверхности образуются прямолинейной образующей,
которая скользит по кривой и проходит через неподвижную точку,
называемую вершиной.
S
Вершина
Образующая L
Частным случаем конической поверхности
является конус вращения, получающийся при
вращении образующей, пересекающейся с осью
вращения
S3
S2
M
(22)
Направляющая
Р2
12
A2
B1=D1
Δ2
(23)
13
N
Ø(MN,S,L) - математический определитель
конической поверхности
D1
[L∩MN; L S] – геометрический
определитель конической поверхности
21
∩
Для построения недостающих проекций точек,
лежащих на поверхности конуса, используются простейшие линии поверхности (прямые,
окружности), проходящие через заданную
точку
C2
A1
S1
11
B1
C1
D3
A3=(C3)
B3

11. Нелинейчатые поверхности

Из множества нелинейчатых поверхностей наиболее широкое применение
имеют поверхности вращения. Поверхности вращения получаются вращением криволинейной образующей вокруг неподвижной оси. Образующая может
быть как плоской, так и пространственной линией.
Ось вращения и образующая кривая составляют определитель поверхности.
Поверхность вращения задана, если заданы проекции ее определителя. Ось
вращения обычно располагается перпендикулярно к одной из плоскостей
проекций. Для большей наглядности на эпюре показывают особые линии каркаса поверхности. Каркас – совокупность параллелей и меридианов поверхности.
Параллели – окружности, описываемые каждой точкой образующей при ее
вращении. Наибольшая параллель называется экватором.
Меридианы – линии, по которым поверхности вращения пересекаются плоскостями, проходящими через ось вращения. Меридиан, параллельный фронтальной проекции, называется фронтальным или главным. Меридиан, параллельный профильной проекции, называется профильным.
Меридианы и параллели используются для построения точек, лежащих на поверхности вращения.
В зависимости от вида образующей различают такие поверхности вращения:
1. Сфера. 2. Эллипсоид вращения. 3. Параболоид вращения. 4. Гиперболоид
вращения.

12.

Сфера (шаровая поверхность) – поверхность, образованная вращением полуокружности вокруг своего диаметра. Особые точки и линии на поверхности сферы:
Экватор – очерк горизонтальной проекции сферы, линия видимости на горизонтальной
проекции (Э).
Главный меридиан (фронтальный меридиан) – очерк фронтальной проекции, линия видимости на фронтальной проекции (Ф.м.).
Профильный меридиан – очерк профильной проекции, линия видимости на профильной проекции (П.м.).
Z
N2
32
12
42
N3
33
P2
(43)
13
22
23
Х
Yп3
Экватор
(21)
11
Профильный
меридиан
N1=S1
31
Фронтальный
меридиан
41
Yп1
Точки 1,2,3 лежат на особых линиях сферы. Их недостающие проекции находятся без вспомогательных линий. Проекции точки 4 находятся на одноименных проекциях параллели, проходящей через
точку 4.