Similar presentations:
Основы динамики поступательного движения механической системы
1.
2.
.1. Законы Ньютона
•Первый закон Ньютона (закон инерции) содержит определение ИСО и
постулат о существовании ИСО. Он гласит:
•существуют такие системы отсчета, называемые инерциальными,
относительно которых свободная материальная точка движется
прямолинейно и равномерно либо покоится.
Мерой инертности материальной точки (тела) является ее масса -
m
m кг
Воздействие на материальную тточку со стороны другой механической системы
(материальной точки, тела) определяется векторной величиной – силой -
F Н
F
3.
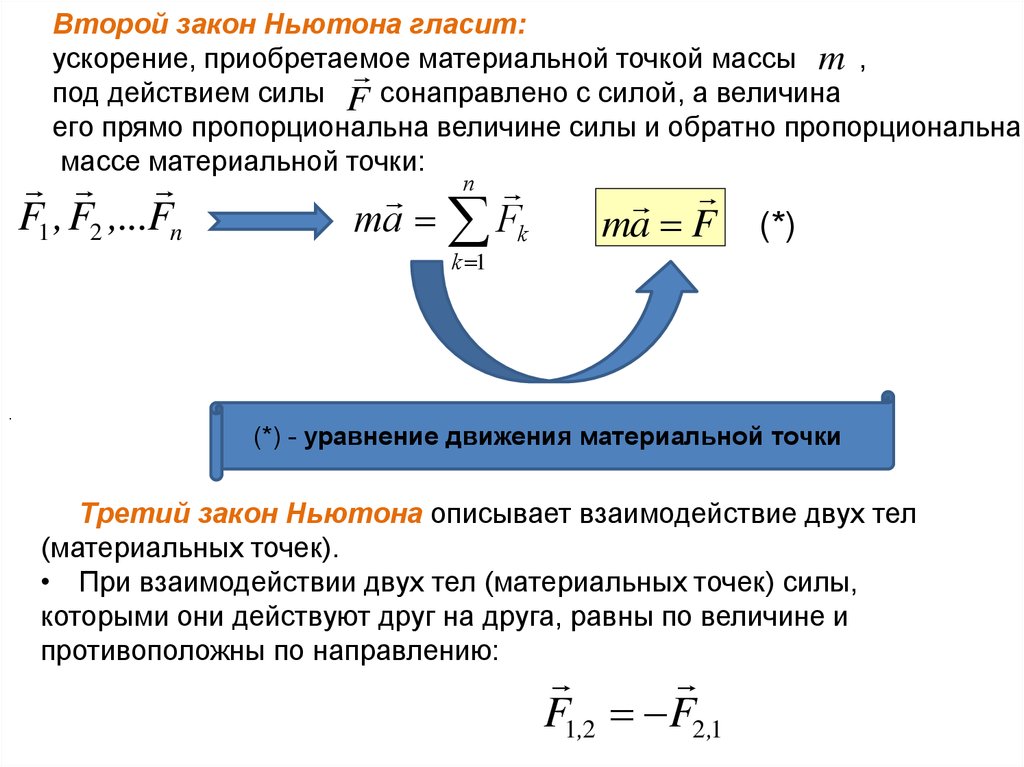
Второй закон Ньютона гласит:ускорение, приобретаемое
материальной точкой массы m ,
под действием силы F сонаправлено с силой, а величина
его прямо пропорциональна величине силы и обратно пропорциональна
массе материальной точки:
F1 , F2 ,...Fn
n
ma Fk
ma F
(*)
k 1
.
(*) - уравнение движения материальной точки
Третий закон Ньютона описывает взаимодействие двух тел
(материальных точек).
• При взаимодействии двух тел (материальных точек) силы,
которыми они действуют друг на друга, равны по величине и
противоположны по направлению:
F1,2 F2 ,1
4.
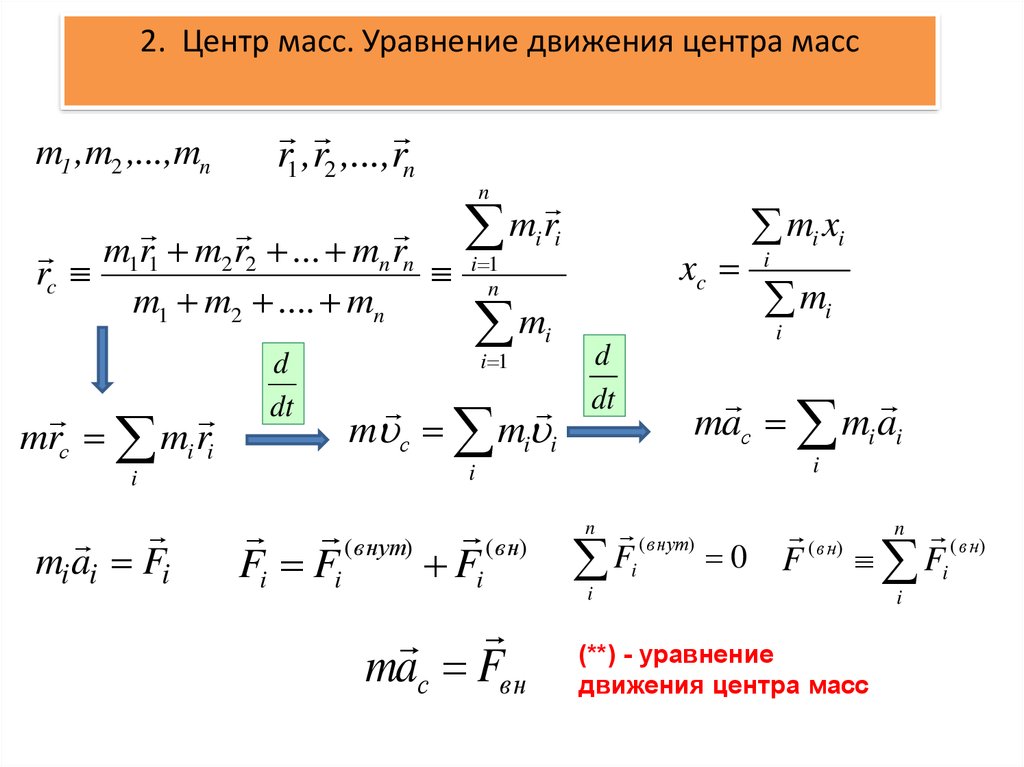
2. Центр масс. Уравнение движения центра массm1 ,m2 ,...,mn
r1 ,r2 ,...,rn
mi ri
n
m1r1 m2 r2 ... mn rn
rc
m1 m2 .... mn
mrс mi ri
i
mi ai Fi
d
dt
xc
i 1
n
m
i 1
i
m с mi i
d
dt
maс Fвн
i
mi
i
maс mi ai
i
i
(внут) (вн)
Fi Fi
Fi
mi xi
( внут)
Fi 0
n
i
( вн) n ( вн)
F Fi
(**) - уравнение
движения центра масс
i
5.
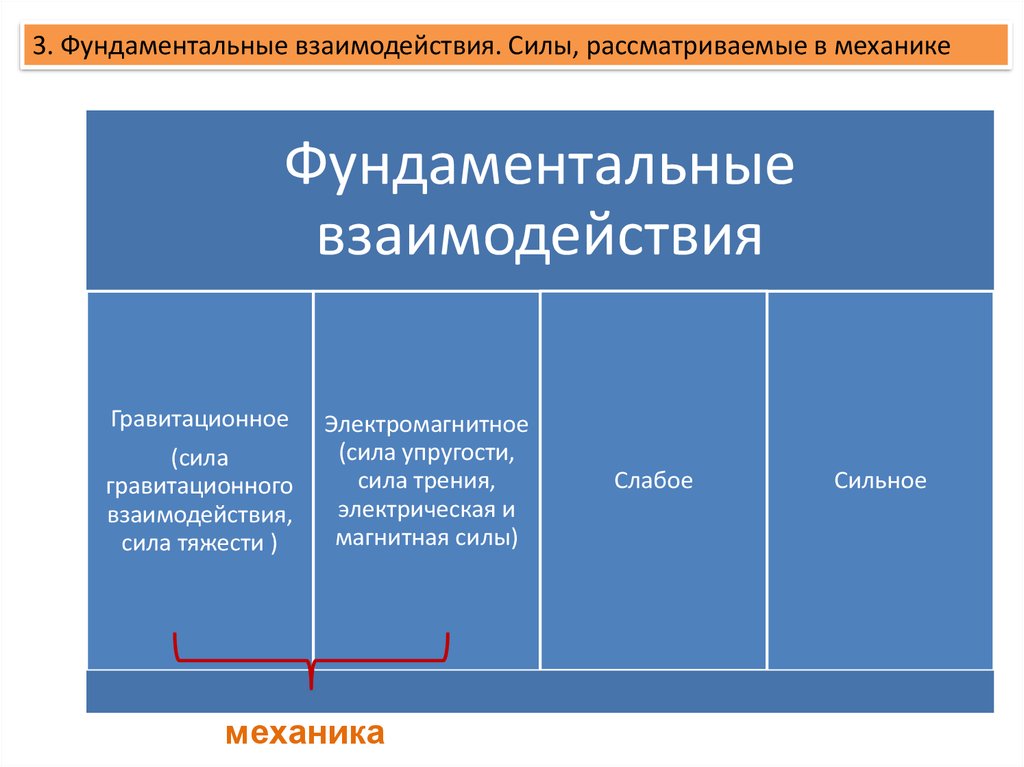
3. Фундаментальные взаимодействия. Силы, рассматриваемые в механикеФундаментальные
взаимодействия
Гравитационное
(сила
гравитационного
взаимодействия,
сила тяжести )
Электромагнитное
(сила упругости,
сила трения,
электрическая и
магнитная силы)
механика
Слабое
Сильное
6.
Силы, рассматриваемые в механикеF kr
( ск )
тр
F
- закон Гука
N
F qE
- сила трения скольжения
- электрическая сила
- магнитная сила
Fл q , B
m1m2
Fгр G 2
r
F
g
m
- гравитационная сила (G 6,67 10 11 м3/Кг∙с2)
- напряженность гравитационного поля (поля силы тяжести)
7.
4. Импульс материальной точкиp m
- второй закон Ньютона на языке
dp
ma импульса:
dt
dp
F
dt
t
p p(t2 ) p(t1 ) F (t )dt
2
Fdt
t1
- импульс силы
p
Fср
t
или
p Fср t
8.
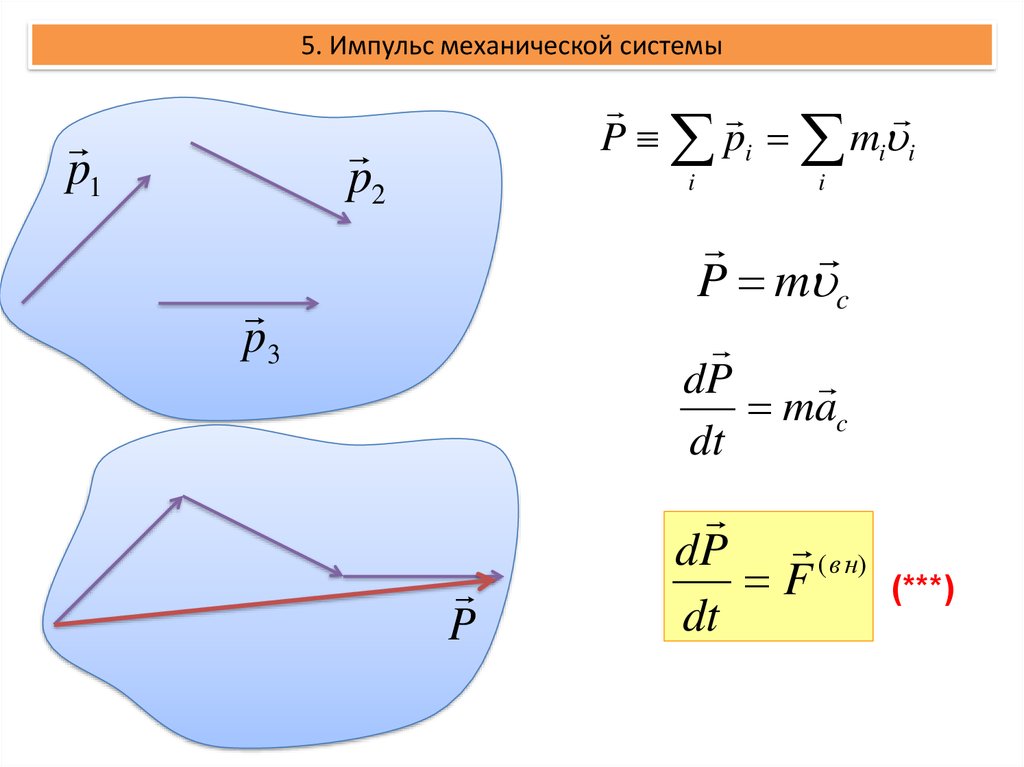
5. Импульс механической системыp1
P pi mi i
p2
i
i
P m c
p3
dP
mac
dt
P
dP (вн)
F
dt
(***)
9.
6. Закон сохранения импульсаЗакон сохранения импульса (з.с.и.) механической системы
легко получается как следствие уравнения движения (***)
dP (вн)
F
dt
( в н)
F
0
P const
- если сумма внешних сил, действующих на систему,
равна нулю, то импульс системы сохраняется.
Традиционная формулировка з.с.и. гласит:
- импульс замкнутой системы сохраняется.
Если внешними силами, действующими на систему, можно
пренебречь, ее можно рассматривать как систему замкнутую.





 physics
physics








