Similar presentations:
Динамика поступательного движения
1. Лекция 2
Тема :Динамика
поступательного
движения
1
2. Домашнее задание
• Прочитать: Учебник, том 1• §§ 6 Динамика поступательного
движения.
• Задачник, т. 1.
• Сделать задачу 3 (стр. 196). Образец
решения смотри в задачнике.
2
3. §6 Динамика материальной точки
• Динамика – раздел механики, вкотором изучают движение тел
с учётом причин, вызывающих
это движение.
3
4. 6.1 Основные характеристики динамики поступательного движения
• 1. Масса (m) – скалярная физическаявеличина, являющаяся мерой
инертных и гравитационных
свойств тела.
• Масса может служить мерой
энергосодержания.
• Единица измерения [m] = кг.
4
5. Основные свойства массы
• масса в классической механике независит от скорости движения;
• масса является величиной аддитивной,
т. е. масса системы тел равняется
сумме масс тел, входящих в систему
m= m1+m2+…+m3;
• масса замкнутой системы остается
величиной постоянной, т.е.
выполняется закон сохранения массы.
5
6. ПЛОТНОСТЬ (читается ро)
ПЛОТНОСТЬ (читается ро)• Плотность ( ) – скалярная
физическая величина,
характеристика вещества,
численно равная массе единицы
объёма:
m
V
• Единица измерения [ ] = кг / м3
6
7. Основные характеристики динамики поступательного движения
• 2. Импульс тела – векторнаяфизическая величина, равная
произведению массы тела на его
скорость:
p mv
• Единица измерения [р] = (кг∙м) / с
• Направление импульса тела совпадает
с направлением скорости.
7
8. Сила F
• 3. Сила (F ) – векторная физическаявеличина, являющаяся мерой
механического воздействия на
тело других тел или полей.
• Единица измерения [F] = Н (ньютон)
• Сила характеризуется модулем
(численным значением), направлением
действия и точкой приложения.
8
9. Сила F
• Действие силы может быть статическими динамическим. Статическое действие
проявляется в возникновении
деформаций, динамическое – в
возникновении ускорений.
• Вид формулы для расчёта силы
зависит от природы взаимодействий.
9
10. 6.2 Виды взаимодействий
• 1. Гравитационное взаимодействие- Универсальное фундаментальное
взаимодействие между всеми
материальными телами имеющими
массу
10
11. 6.2 Виды взаимодействий
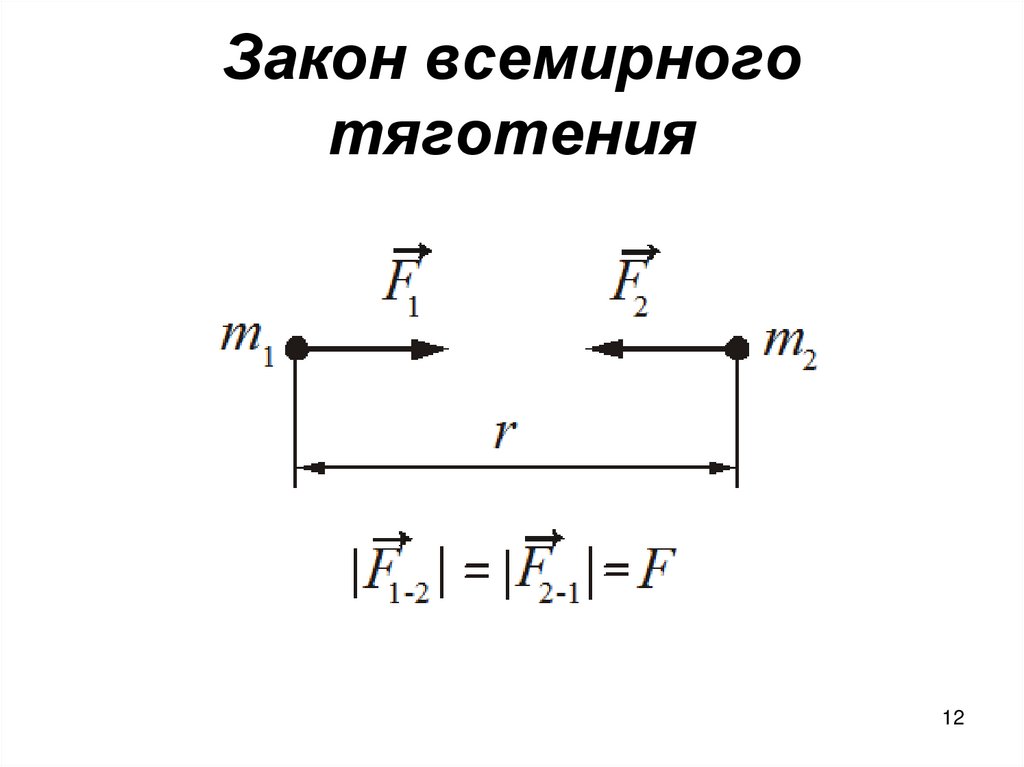
• Закон всемирного тяготения.• Две материальные точки массами m1 и
m2 притягиваются друг к другу с силой
прямо пропорциональной массам этих
точек и обратно пропорциональной
квадрату расстояния между ними
F G
m1 m2
r
2
11
12. Закон всемирного тяготения
1213. Сила тяжести
• Сила тяжести — сила, действующая налюбое физическое тело, находящееся
вблизи поверхности Земли
Fтяжести F mg
• Гравитационное взаимодействие
осуществляется посредством
гравитационного поля.
13
14. Гравитационное поле
• Поле – это особая форма материи,которая проявляет себя силовым
действием на другие тела. Одно тело
изменяет свойства окружающего
пространства, т. е. создаёт в нём
гравитационное поле. Второе тело,
находящееся вблизи первого,
испытывает со стороны
гравитационного поля некоторую силу в
том месте, где оно находится.
14
15. Электромагнитное взаимодействие
• Электромагнитное взаимодействиесуществует между частицами,
обладающими электрическим зарядом.
С современной точки зрения
электромагнитное взаимодействие
между заряженными частицами
осуществляется не прямо, а только
посредством электромагнитного поля.
15
16. Электромагнитное взаимодействие
• Частными случаями проявленияэлектромагнитных взаимодействий
являются силы упругости и силы
трения.
• Для сил упругости и трения можно
получить лишь приближённые,
эмпирические (т. е. основанные на
опыте) формулы.
16
17. силы упругости
• Под действием внешних сил возникаютдеформации (т. е. изменение размеров
и формы тел).
• Если после прекращения действия сил
прежняя форма и размеры тела
восстанавливаются, то деформация
называется упругой.
17
18. Закон Гука
• Сила упругости пропорциональнаабсолютному удлинению
Fупр kx
• k – жёсткость пружины;
• х – абсолютное удлинение пружины.
18
19. Закон Гука (другая формулировка)
• Механическое напряжение прямопропорционально относительному
удлинению
Е
• Е – модуль упругих деформаций
(модуль Юнга);
• - относительное удлинение
19
20. обозначения
• Абсолютное удлинениеx l l l0
• Относительное удлинение
l
l
• Механическое напряжение
F
S
20
21. Закон сухого трения
• Трение между поверхностями двухсоприкасающихся твёрдых тел при
отсутствии между ними жидкой или
газообразной прослойки, называется
сухим трением.
• Трение скольжения – трение при
относительном движении
соприкасающихся тел.
21
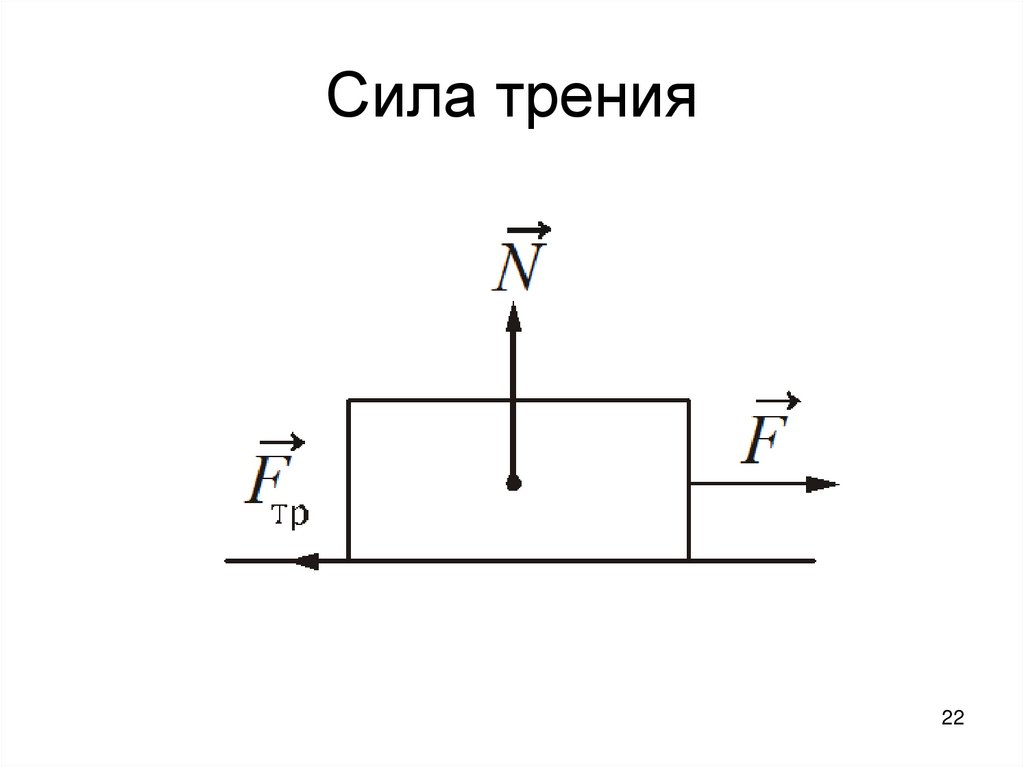
22. Сила трения
2223. Закон сухого трения
• Сила трения скольженияпропорциональна силе нормальной
реакции опоры и не зависит от
площади соприкосновения тел:
Fтр N
• где – коэффициент трения
скольжения
23
24. Закон вязкого трения
• На тело, движущееся в вязкой (жидкойили газообразной) среде, действует
сила, тормозящая его движение. Эта
сила называется силой вязкого
трения:
F r v
• r – коэффициент сопротивления;
• v – скорость движения тела.
24
25. Закон Архимеда
• На тело, погружённое в жидкость(газ), действует выталкивающая
сила, равная весу вытесненной
телом жидкости (газа)
FA ж gV
• где ж – плотность жидкости (газа);
• V – объём погружённой части тела.
25
26. Сложение сил
• Равнодействующей нескольких силназывается сила, действие которой
эквивалентно одновременному
действию этих сил. Равнодействующая
равна векторной сумме действующих
сил:
F F1 F2
• Складываются силы по правилу
параллелограмма
26
27. Сложение сил
2728. Сложение сил
• модуль равнодействующей двух силрассчитывается по формуле
F
2
2
F1 F2 2F1F2 cos
28
29. Разложение сил
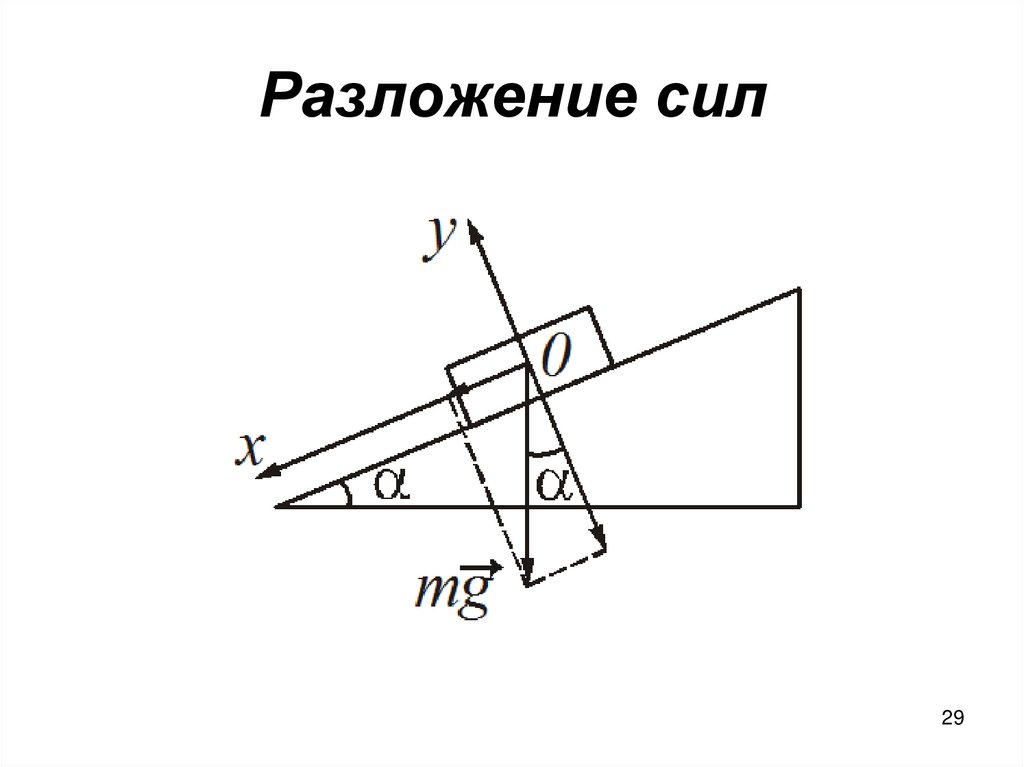
2930. Разложение сил
• Разложение вектора на составляющиесостоит в замене вектора двумя или
несколькими векторами, сумма которых
равна данному вектору.
Fx (mg) x mg sin
Fy (mg ) y mg cos
30
31. 6.5 Основные законы динамики материальной точки (законы Ньютона)
• Динамика базируется на законахНьютона, которые математически не
выводятся, а являются обобщением
опыта.
31
32. 6.5.1 Первый закон Ньютона
• Всякое тело сохраняет состояниепокоя или равномерного
прямолинейного движения до тех
пор, пока воздействия со стороны
других тел не изменят этого
состояния.
• Свойство тел сохранять состояние
своего движения называется инерцией.
32
33. 6.5.2 Второй закон Ньютона
• Скорость изменения импульса теларавна равнодействующей всех сил,
действующих на тело:
dp
F
dt
• Масса тела остается постоянной
m=const, то
F ma
33
34. 6.5.3 Третий закон Ньютона
• Силы, с которымивзаимодействуют два тела, равны
по величине и противоположны по
направлению:
F12 F21
• Силы всегда возникают попарно,
поэтому говорят о взаимодействии .
34
35. 6.6 Динамика системы материальных точек
• Совокупность материальных точек(тел), выделенных для рассмотрения,
называется механической системой.
• Рассмотрим систему тел, которые
взаимодействуют как между собой, так
и с внешними телами.
35
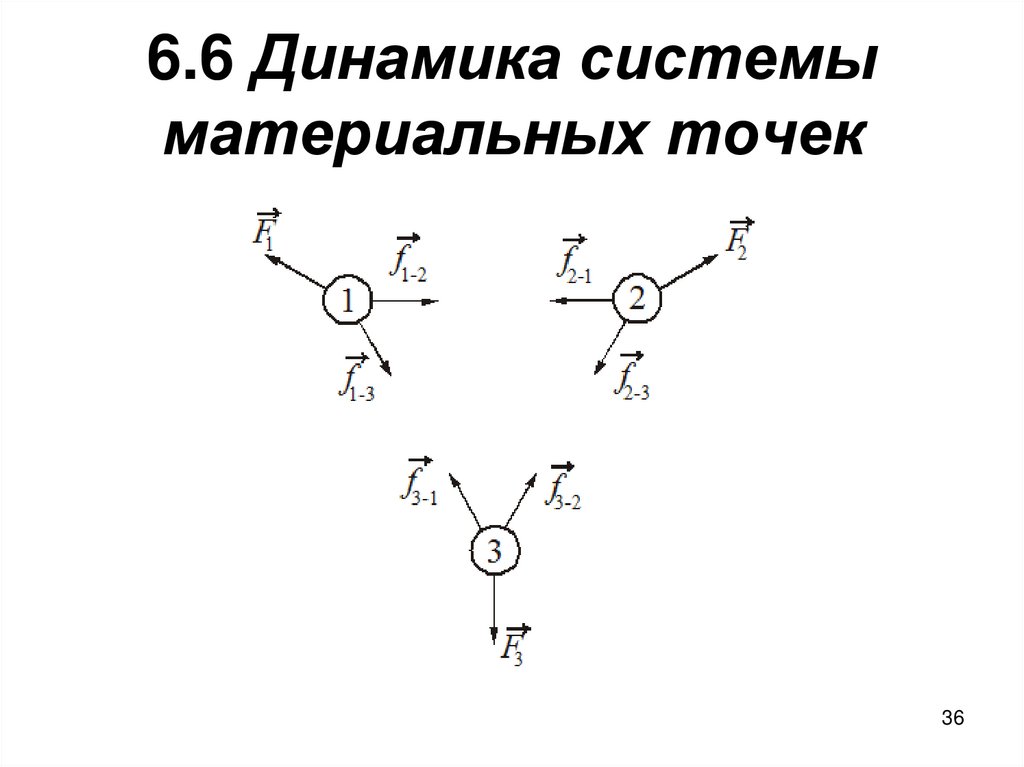
36. 6.6 Динамика системы материальных точек
3637. 6.6 Динамика системы материальных точек
• Для каждого тела запишем второйзакон Ньютона. Сложив уравнения
почленно, получим
d ( p1 p2 p3 )
F1 F2 F3
dt
• где p1 p2 p3 - сумма импульсов
системы тел.
37
38. 6.6 Динамика системы материальных точек
• F1 F2 F3 - сумма внешних сил.• Если она равна нулю, то такая система
называется замкнутой.
• Тогда d ( p1 p2 p3 ) 0
dt
• Это означает p1 p2 p3 const
т.е. получили закон сохранения импульса
38
39. Закон сохранения импульса
• Импульс замкнутой системы телостается постоянным (const).
• То, что величина остаётся const,
означает , что можно записать
m1v1 m2 v2 m1u1 m2u2
• где v и u – скорости до и после
взаимодействия
39



































 physics
physics








