Нормальное и тангенциальное ускорение. Динамика поступательного движения. Закон сохранения импульса. (Лекция 2)

1. Лекция 2

1

2.

Содержание предыдущей лекции
Введение.
• Физика в системе естественных наук.
• Физика и научно-технический прогресс.
• Роль физики в образовании.
• Общая структура и задачи дисциплины «Физика».
Кинематика поступательного движения.
• Пространство и время в механике Ньютона.
• Основные характеристики криволинейного
движения: скорость и ускорение.
2

3.

Содержание сегодняшней лекции
• Нормальное и тангенциальное ускорение.
Динамика поступательного движения.
Закон сохранения импульса.
Инерциальные системы отсчета.
Законы Ньютона.
Масса, импульс, сила.
Уравнение движения материальной точки.
Понятие замкнутой системы.
Закон сохранения импульса.
Центр масс механической системы, закон движения центра
масс.
• Движение тел переменной массы. Уравнение Мещерского.
3

4.

Ускорение
v dv
a lim
v
t 0 t
dt
dvx
dv
ax
v x
dt пр. x dt
dx
v x x
dt
dvx d dx d x
2 x
dt dt dt dt
2
4

5.

Ускорение
v v
в сторону вектора v ,
- единичный вектор (орт), направленный
v – модуль вектора v
d
a (v )
dt
a v v
5

6.

a v v
Нормальное и тангенциальное ускорения
a v - тангенциальное (касательное) ускорение.
an v - нормальное ускорение.
a a an
6

7.

a v
Тангенциальное ускорение
v 0 :
a
a v
a v
v 0 :
v 0 : равномерное движение, a 0.
a
7

8.

an v
-
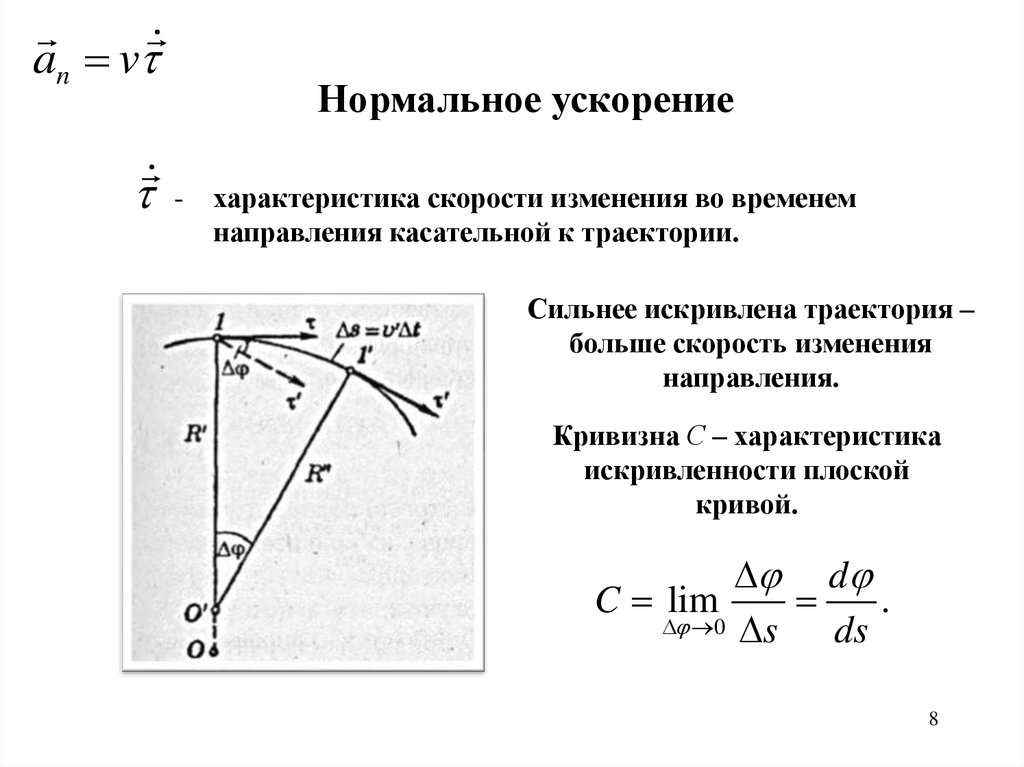
Нормальное ускорение
характеристика скорости изменения во временем
направления касательной к траектории.
Сильнее искривлена траектория –
больше скорость изменения
направления.
Кривизна С – характеристика
искривленности плоской
кривой.
d
C lim
.
0 s
ds
8

9.

an v
Нормальное ускорение
1
s ds
.
Радиус кривизны R lim
C 0 d
Радиус кривизны – радиус
окружности, которая
сливается в данном месте с
кривой на бесконечно
малом ее участке.
9

10.

an v
Нормальное ускорение
s v t
R
R
t 0
1
2
0
n
10

11.

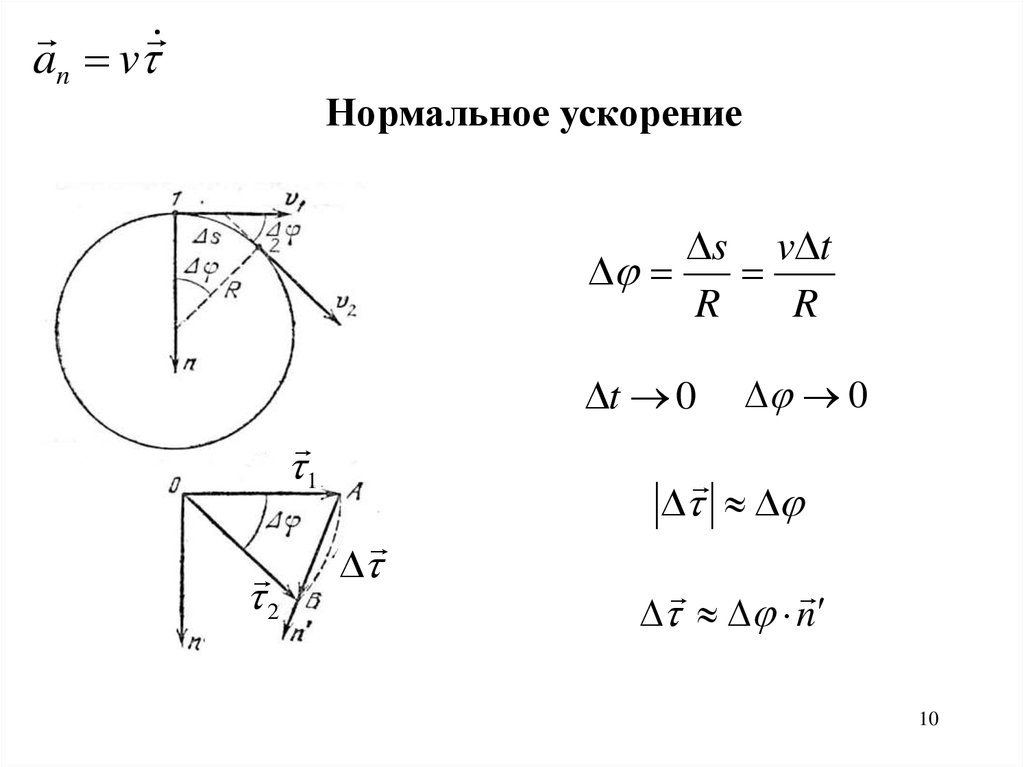
an v
s v t
R
R
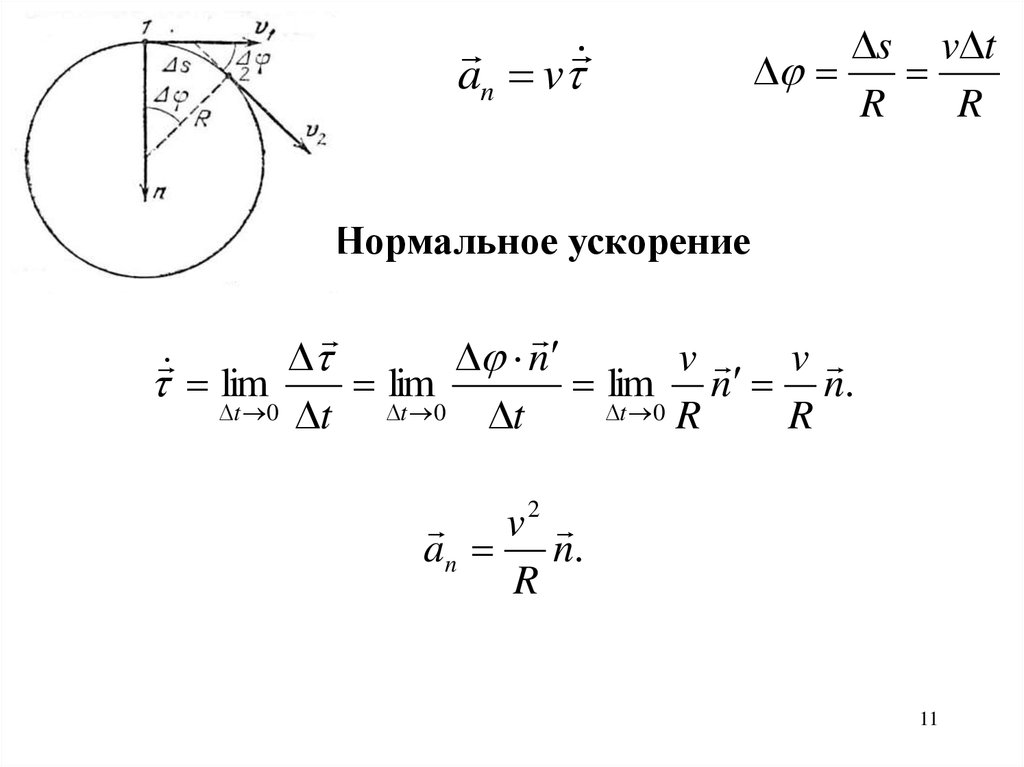
Нормальное ускорение
n
v v
lim
lim
lim n n.
t 0 t
t 0
t 0 R
t
R
v2
a n n.
R
11

12.

Тангенциальное и нормальное ускорения
v2
a a an v n.
R
a a a
2
2
n
v
2
2
v /R .
2
12

13.

Динамика поступательного движения
Динамика – изучение движения тел с учетом причин,
вызвавших это движение.
Причины, вызвавшие движение, взаимодействие между телами.
13

14.

Инерциальные системы отсчета
Разный характер движения тел
относительно разных систем отсчета.
Движение точки
на пере лопатки ротора двигателя летящего самолета:
- по окружности относительно корпуса двигателя,
14
- вдоль синусоиды относительно Земли.

15.

Инерциальные системы отсчета
Инерциальные системы отсчета –
системы отсчета, относительно которых тела,
не подверженные воздействию других тел,
движутся без ускорения, т.е. прямолинейно и равномерно.
Наиболее простое движение тел относительно инерциальных систем отсчета.
Существование инерциальных систем отсчета –
закон природы.
15

16.

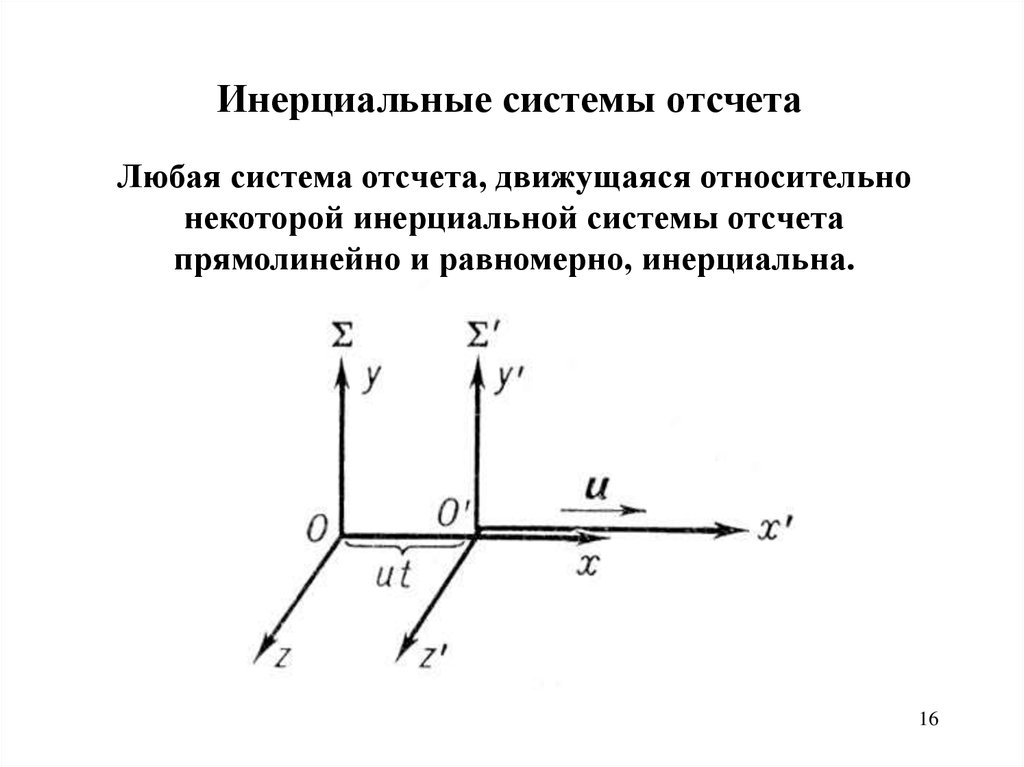
Инерциальные системы отсчета
Любая система отсчета, движущаяся относительно
некоторой инерциальной системы отсчета
прямолинейно и равномерно, инерциальна.
16

17.

Инерциальные системы отсчета
17

18.

Инерциальные системы отсчета
Эксперимент - гелиоцентрическая система отсчета
с очень высокой степенью точности инерциальна.
18

19.

Инерциальные системы отсчета
Геоцентрическая система отсчета
не является инерциальной –
Земля движется вокруг Солнца
по криволинейной траектории и вращается вокруг своей оси.
Возможность пренебречь неинерциальностью
геоцентрической системы отсчета во многих случаях.19

20.

Первый закон Ньютона
Закон инерции (первый закон Ньютона) –
утверждение о существовании инерциальных систем отсчета.
Всякое тело находится в состоянии покоя или
равномерного и прямолинейного движения,
пока воздействие со стороны других тел
не заставит его изменить это состояние.
20

21.

Масса, импульс, сила
Ускорение тела (изменение скорости) –
результат его взаимодействия с другими телами.
21

22.

Масса, импульс, сила
Разное ускорение тел при одинаковом воздействии на них.
Масса тела – мера инертности, отклика на воздействие.
22

23.

Масса, импульс, сила
Замкнутая система - система, в которой отсутствует обмен
веществом, энергией и информацией с внешней средой или
окружением.
Изолированная система – допускается обмен информацией
с внешней средой, но не энергией и веществом.
Закрытая система – допускается обмен энергией с внешней
средой, но не веществом и информацией.
23

24.

Масса, импульс, сила
Замкнутая система тел – система тел, взаимодействующих
между собой и не взаимодействующих с другими телами.
Эксперимент: отношение модулей приращения скоростей
при взаимодействии двух тел в замкнутой системе
не зависит от способа и интенсивности взаимодействия
данных двух тел, а зависит только от их масс:
v 1 m2
.
v2 m1
24

25.

v 1 m2
v2 m1
Масса, импульс, сила
Более инертное тело (тело с большей массой) –
меньшее изменение скорости.
С учетом направления
m1 v1 m2 v2 .
25

26.

m1 v1 m2 v2
Масса, импульс, сила
Ньютоновская механика (v << c):
масса тела - постоянная физическая величина,
не зависящая от скорости тела.
С учетом этого
(m1v1 ) (m2v2 ).
p mv - импульс тела.
p1 p2
26

27.

p1 p2
Масса, импульс, сила
p1 p2 0
p p1 p2
p - постоянная величина.
Полный импульс замкнутой системы
двух взаимодействующих тел остается постоянным.
27

28.

p mv
Второй закон Ньютона
Эксперимент: равенство скорости изменения импульса тела
действующей на него силе.
dp
F
dt
- уравнение движения тела.
mv ma F
Равенство произведения массы тела на его ускорение
действующей на тело силе.
28

29.

mv ma F
Первый закон Ньютона
Если F 0, то a 0.
Первый закон Ньютона – следствие второго закона Ньютона.
29

30.

Третий закон Ньютона
Если тело 1 действует на тело 2 с силой F21 ,
то тело 2 действует на тело 1 с силой F12 ,
F12 F21.
30

31.

Третий закон Ньютона
31

32.

Закон сохранения импульса
Система из N взаимодействующих частиц.
Fik внутренние силы, действующие на i-ую частицу,
Fi результирующая внешних сил, действующих на i-ую
частицу.
Броуновские
частицы
32

33.

Закон сохранения импульса
Уравнения движения для всех N частиц:
N
p1 F12 F13 ... F1k ... F1N F1 F1k F1 ,
k 2
N
p2 F21 F23 ... F2 k ... F2 N F2
F2k F2 ,
k 1
( k 2)
........................................................................................
N
pi Fi1 Fi 2 ... Fik ... FiN Fi Fik Fi ,
k 1
( k i )
........................................................................................
p N FN 1 FN 2 ... FNk ... FN , N 1 FN
FNk FN .
N
k 1
(k N )
33

34.

Закон сохранения импульса
Операция:
сложение всех левых и всех правых частей уравнений.
В правой части F12 F21 0 (третий закон Ньютона) и т.д.
Результат сложения:
N
d
p1 p2 ... pN F1 F2 ... FN Fi .
dt
i 1
d N
p Fi ,
dt
i 1
N
N
где p pi mi vi - импульс системы.
i 1
i 1
34

35.

Закон сохранения импульса
d N
p Fi ,
dt
i 1
Постоянство импульса системы в случае ее замкнутости.
Постоянство импульса системы в случае незамкнутости
системы, но равенства нулю равнодействующей внешних сил.
35

36.

d N
p Fi ,
dt
i 1
Закон сохранения импульса
Басня И.А. Крылова:
Однажды Лебедь, Рак, да Щука
Везти с поклажей воз взялись,
И вместе трое все в него впряглись;
Из кожи лезут вон, а возу все нет ходу!
Причина сохранения импульса (отсутствия движения) –
равнодействующая внешних сил,
действующих на воз с поклажей, равна нулю:
Лебедь рвётся в облака, Рак пятится назад, а Щука тянет в воду,
сила тяжести уравновешивается силой реакции опоры.
36

37.

Закон сохранения импульса
Постоянство проекции импульса
на некоторое направление x в случае равенства нулю
проекции на это направление
суммы действующих на систему внешних сил.
N
d
p x Fxi .
dt
i 1
37

38.

Закон сохранения импульса
Центр масс (центр инерции) системы материальных точек –
точка С, положение которой задается радиусом-вектором
m1r1 m2 r2 ... mN rN mi ri mi ri
rC
.
m1 m2 ... mN
m
mi
38

39.

m1r1 m2 r2 ... mN rN
rC
m1 m2 ... mN
mi ri
m
i
mi ri
m
Закон сохранения импульса
Скорость центра масс vC rC
mi ri
m
mi vi
m
p
.
m
Импульс системы частиц p mvC .
Следствие закона сохранения импульса –
центр масс замкнутой системы либо движется
прямолинейно и равномерно, либо остается неподвижным.
39

40.

vC rC
mi ri
m
mi vi
m
p
m
d N
p Fi ,
dt
i 1
Закон сохранения импульса
Соответствие движения центра масс системы
движению материальной точки с массой,
равной массе тел системы,
под действием равнодействующей приложенных внешних сил.
maC F внешн .
40

41.

Движение тел переменной массы
Переменная масса – масса относительно медленно
движущихся тел, меняющаяся за счет потери или
приобретения вещества.
41

42.

Движение тел переменной массы
Уравнения движение тел переменной массы –
следствие законов Ньютона.
Выброс с большой скоростью ракетой
создаваемых в результате сгорания
топлива газов.
Действие выбрасываемых газов на ракету с равной,
но противоположно направленной силой.
Результат - ускорение ракеты.
42

43.

Движение тел переменной массы
Ракета и выброшенное вещество –
замкнутая система.
Сохранение во времени импульса
данной замкнутой системы в отсутствие внешних сил следствие выполнения закона сохранения импульса
замкнутой системы тел.
43

44.

Движение тел переменной массы
Более общий случай – наличие действующих
на систему внешних сил
( F - геометрическая сумма всех внешних сил,
действующих на ракету).
Пример: движение ракеты под действием
гравитационных полей Земли, Солнца, планет,
сопротивления атмосферы.
44

45.

Движение тел переменной массы
m(t) – масса ракеты в произвольный момент времени,
v (t ) – скорость ракеты в тот же момент времени,
mv – импульс ракеты в тот же момент времени,
dm < 0 и dv – приращения массы и скорости ракеты
за время dt,
m dm v dv – импульс ракеты в момент времени t + dt,
dmгаз vгаз – импульс газов, образовавшихся за время dt.
45

46.

d N
p Fi
dt
i 1
Движение тел переменной массы
Приращение импульса системы за время dt
p p(t dt ) p(t ).
Согласно второму закону Ньютона,
p m dm v dv dmгаз vгаз - mv Fdt.
46

47.

m dm v dv dmгазvгаз - mv Fdt
Движение тел переменной массы
mv dmv mdv dmdv dmгаз vгаз mv Fdt.
Пренебрегаем бесконечно малой высшего порядка dmdv.
Учитывая закон сохранения массы dm dmгаз 0,
заменяем dmгаз dm.
Учитываем, что скорость истечения газов относительно
ракеты (скорость газовой струи)
vотн vгаз v .
Получаем mdv vотнdm Fdt.
47

48.

mdv vотн dm Fdt
Движение тел переменной массы
Уравнение Мещерского
или уравнение движения точки с переменной массой
dv dm
m
vотн
F.
dt
dt
Внешние силы
Реактивная
сила
Российский и
советский ученый
И.В. Мещерский
(1859-1935)
Труды по механике тел переменной массы –
теоретическая основа разработки многих
проблем реактивной техники.
48

49.

Контрольный вопрос
Нормальное ускорение мяча, который выронил ребенок,
равно:
а) 0,
б) 9,8 м/с2,
в) -9,8 м/c2?
49

50.

Контрольный вопрос
Вы прижимаете учебник по физике к вертикальной стене.
Сила трения, действующая со стороны стены на учебник,
направлена:
а) вниз,
б) вверх,
в) в сторону книги,
г) в сторону стены.
50